基于EMD-MFOA-ELM的瓦斯涌出量时变序列预测研究*

卢国斌，李晓宇，祖秉辉，董建军

(1.辽宁工程技术大学 矿业学院，辽宁 阜新 123000；2.矿山热动力灾害与防治教育部重点实验室，辽宁 阜新 123000；3.辽宁工程技术大学 矿业技术学院，辽宁 葫芦岛 125100)

0　引言

瓦斯是危害煤矿安全生产的主要不安全因素之一，多年来一直是采矿领域重要研究对象[1]。瓦斯涌出作为导致瓦斯灾害的主要来源，其自身携带诱导灾害发生的大量信息，在多种非线性因素的综合作用下，瓦斯涌出表现出显著的非平稳性[2]。因此，以深度挖掘工作面绝对瓦斯涌出量本质结构为出发点，依据监测资料及时掌握瓦斯涌出量变化规律，实现精准动态预测，对于煤矿瓦斯灾害的防治具有重要意义。

近些年，国内外学者针对瓦斯涌出量预测方法进行了深入的研究，取得了丰硕的研究成果：付华[3]等提出利用改进的粒子群算法(MPSO)优化加权最小二乘支持向量机(WLS-SVM),建立瓦斯涌出量的非线性系统，实现涌出量的动态预测；单亚峰[4]等基于相空间重构和改进的极端学习机方法，构建瓦斯涌出量的混沌时间序列预测模型；樊保龙[5]等提出利用LMD方法获取生产函数分量，对各分量建立SVM模型，进行工作面瓦斯涌出量预测；李胜[6]等提出构建基于主成分分析法和改进的果蝇优化支持向量机的回采工作面绝对瓦斯涌出量预测模型；刘俊娥[7]等通过EMD分解获得IMF分量，对每个分量分别进行SVM函数拟合，然后等权叠加重各分量预测值，获得最终预测结果。上述模型从一定程度体现了瓦斯涌出量的非平稳特征，然而并未从时序样本本身挖掘深层次的物理机制。模型的固有缺陷、样本数据的差异等严重影响预测结果，因此，模型在瓦斯涌出量非平稳特征本质分析及预测精度上有待进一步提高。

鉴于此，笔者提出将EMD和MFOA-ELM有机耦合，构建基于EMD-MFOA-ELM的工作面瓦斯涌出量多尺度时变预测模型。采用EMD将瓦斯涌出量时变序列分解出多个IMF分量，运用MFOA-ELM模型对各IMF分量进行外推预测，等权叠加各预测值，重构最终预测结果，结合晋城某矿具体实例进行仿真实验，验证模型的有效性。

1　预测模型相关理论

1.1　EMD基本原理

经验模态分解(EMD)是1998年由Huang 等提出[8-9]，该方法通过分解时变序列获得内部数据的特征时间尺度并以固有波动模式展现，省去选取不同基函数的影响，更加真实地反应时变序列的本质结构。

EMD对时变序列分解步骤如下：

1) 假设时变序列为x(t)，求解出序列中所有的局部极值点，采用3次样条曲线拟合出上下包络线，并计算出包络线的平均值，设为m1(t)，则原始序列x(t)和m1(t)的差值为第一个分量，记作h1(t)：

h1(t)=x(t)-m1(t)

(1)

2) 如果h1(t)满足IMF分量条件，记h1(t)为第一个IMF分量，否则将h1(t)作为原始序列重复上述操作，即：

h11(t)=h1(t)-m11(t)

(2)

3) 重复上述步骤，进行k次筛选，直到h1k(t)满足IMF条件为止。令h1k(t)=c1(t)，则c1(t)为含有原始序列最佳范围或最短周期成分的第1阶IMF分量。

4) 将c1(t)从原始时变序列x(t)中分离出去得：

r1(t)=x(t)-c1(t)

(3)

式中:r1(t)表示残余量。将r1(t)作为新的原始序列并重复以上步骤，得到x(t)的第2阶IMF分量，如此进行n次循环，得到原始序列x(t)的n个IMF分量，其表达式为：

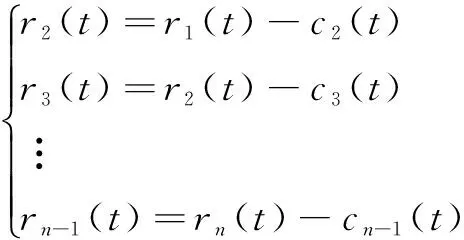
(4)

5) 当rn(t)循环过程中无法再分解出满足IMF条件的分量时，循环结束，最终得到原始序列x(t)的表达式为：

(5)

1.2　ELM基本原理

极限学习机(ELM)是一种新型的前馈神经网络的学习算法，模型结构简单、学习效率和泛化能力高，具有极强的非线性逼近能力[10-11]。

假设对于任意M个不同样本(xi,ti)，其中xi=(xi1,…,xin)∈Rm，ti=(ti1,…,tin)∈Rm，假设隐含层神经元个数为p，则其标准形式如下：

αi=(αi1,…,αin)T(6)

基于零误差逼近原则[12]，在该馈神经网络中存在参数ai，bi，βi使得：

(7)

上式可简化为：Hβ=Y，H为隐含层的输出矩阵。

若在学习机中随机给定输出阀值和权值，则矩阵H就确定下来，ELM的训练可以转化成求解输出权值矩阵的最小二乘解的问题。输出权值矩阵β可以根据β′=H+Y′解得。其中H+表示隐含层输出矩阵H的Moore Penrose广义逆。

1.3　MFOA-ELM耦合算法

果蝇优化算法(fruit fly optimization algorithm, FOA)是根据果蝇觅食动态行为提出的一种全局优化的新算法[13]。通过仿真果蝇利用味道浓度来寻找食物，将目标寻优过程与味道浓度迭代更新过程有机耦合，求取目标的最优解[14-15]。

利用三维寻优模型MFOA优化ELM网络中随机产生的w和b，以期获取最优的w和b，从而提高预测模型的优越性。具体优化步骤如下：

1) 初始化果蝇群体基础参数，假设果蝇群体个数为M，极限迭代次数为N，随机赋值果蝇初始位置(X1,Y1,Z1)，并且每个果蝇个体都携带待优化参数w和b。

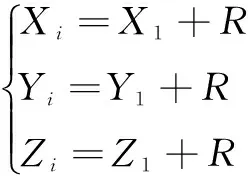
(8)

其中：R为随机参数，i=1,2,…,M。

2) 由于无法获得食物源的具体位置，对果蝇与原点的距离L进行估计，进而计算味道浓度判定值S。

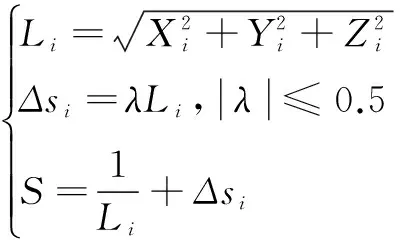
(9)

3)q(xij)为交叉回归预测值，yij为样本真实值，采用3折交叉对训练样本进行验证，计算果蝇个体的味道浓度Ft(适应度值)：

(10)

4) 在果蝇群体中寻找味道浓度最优的个体。

[fbest,findex]=min(Ft(i))

(11)

(5) 保留味道浓度最优值和果蝇相应位置坐标(Xb,Yb,Zb)，其他果蝇通过视觉感应飞往该方向。

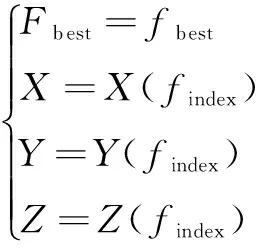
(12)

6) 重复步骤(2)～(5)进行迭代寻优，同时判定味道浓度Ftj+1是否优于Ftj，如果是进行步骤(5)，否则继续迭代，直至达到最大迭代次数。

2　瓦斯涌出量的EMD-MFOA-ELM预测方法

将EMD算法和MFOA-ELM模型进行耦合，构建瓦斯涌出量的EMD-MFOA-ELM时变预测模型。

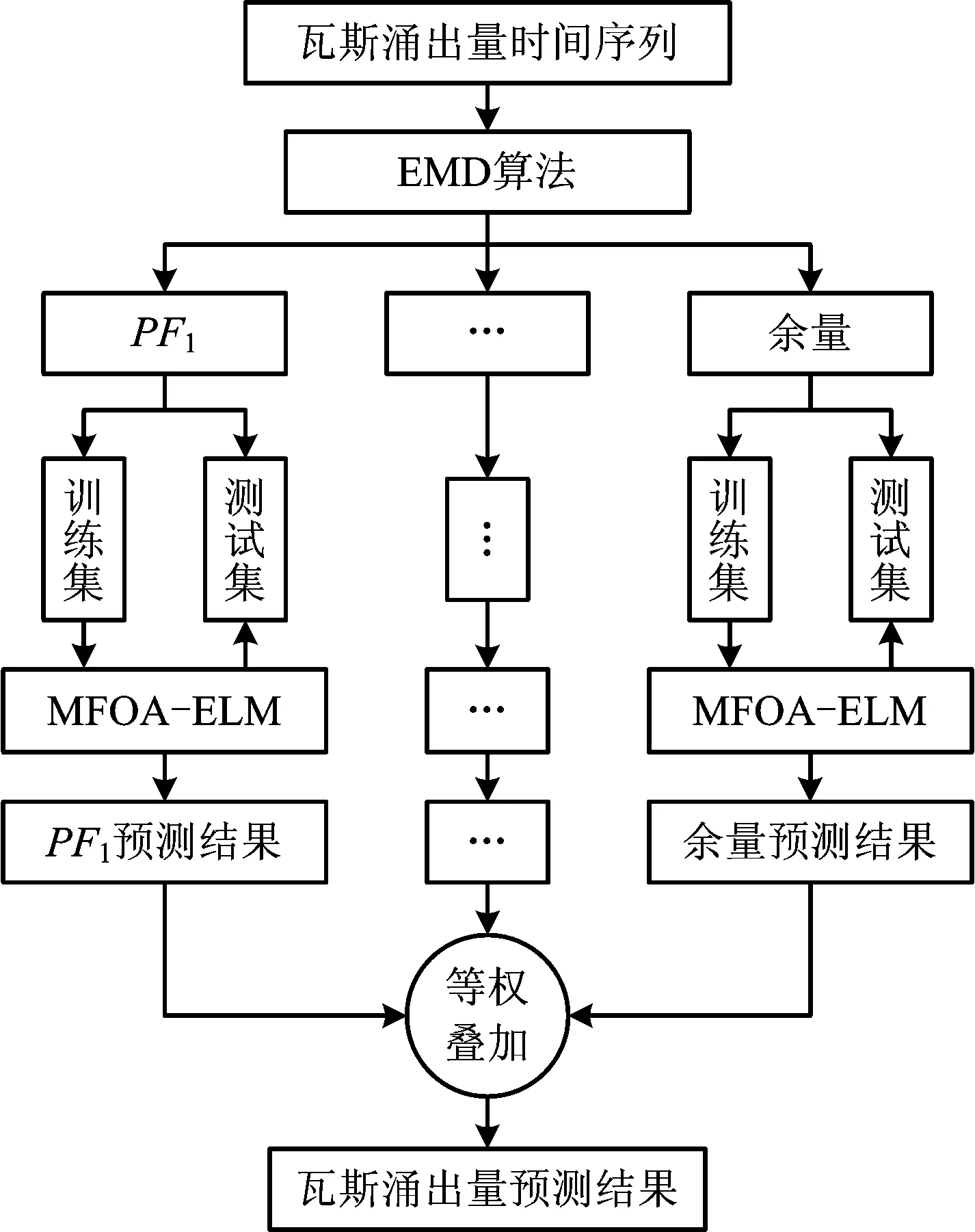
图1　基于EMD-MFOA-ELM耦合模型预测流程Fig.1　Prediction process based on EMD-MFOA-ELM coupling model

一般将煤矿瓦斯涌出量时变序列记作为x(t),(t=1,2,…,m)，具体预测过程如下：

1) 采用EMD算法对原始瓦斯涌出量时变样本进行预处理，将时变序列x(t)进行分解获得n个IMF分量ci(t)(i=1,2,…,n)和一个余量rn。

2) 初始化MFOA-ELM模型的基础参数，将各分量和余量划分成训练集和测试集，采用相空间重构方法将各分量和余量的训练集进行空间重构，利用MFOA-ELM网络模型对重构后的训练集进行学习，寻求最佳模型参数。应用最优的MFOA-ELM模型对各分量的测试集进行预测。

3) 根据等权求和的原则，将各分离信号的预测结果进行叠加，得到瓦斯涌出量时变序列的最终预测结果。

3　应用与分析

以晋煤集团某高瓦斯矿井工作面2016年6月份的瓦斯涌出量观测数据为原始时变序列进行预测实验，样本序列如图2所示，其中绝对瓦斯涌出量为3.80～7.70 m3/min，平均涌出量为5.51 m3/min。经后EMD算法对原始涌出量时变序列进行预处理，处理结果如图3所示。

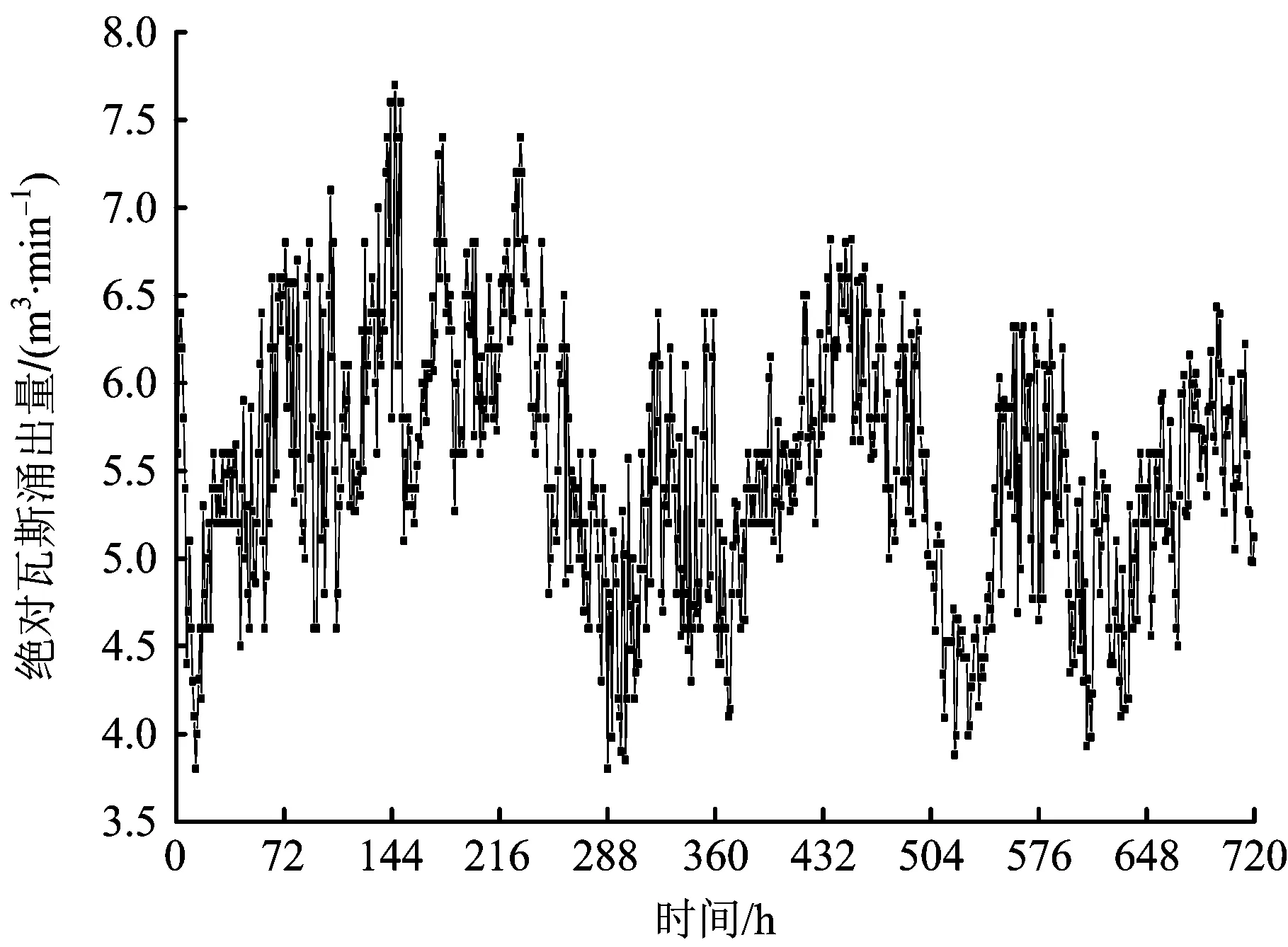
图2　原始绝对瓦斯涌出量时间序列Fig.2　Time series of original absolute gas emission quantity

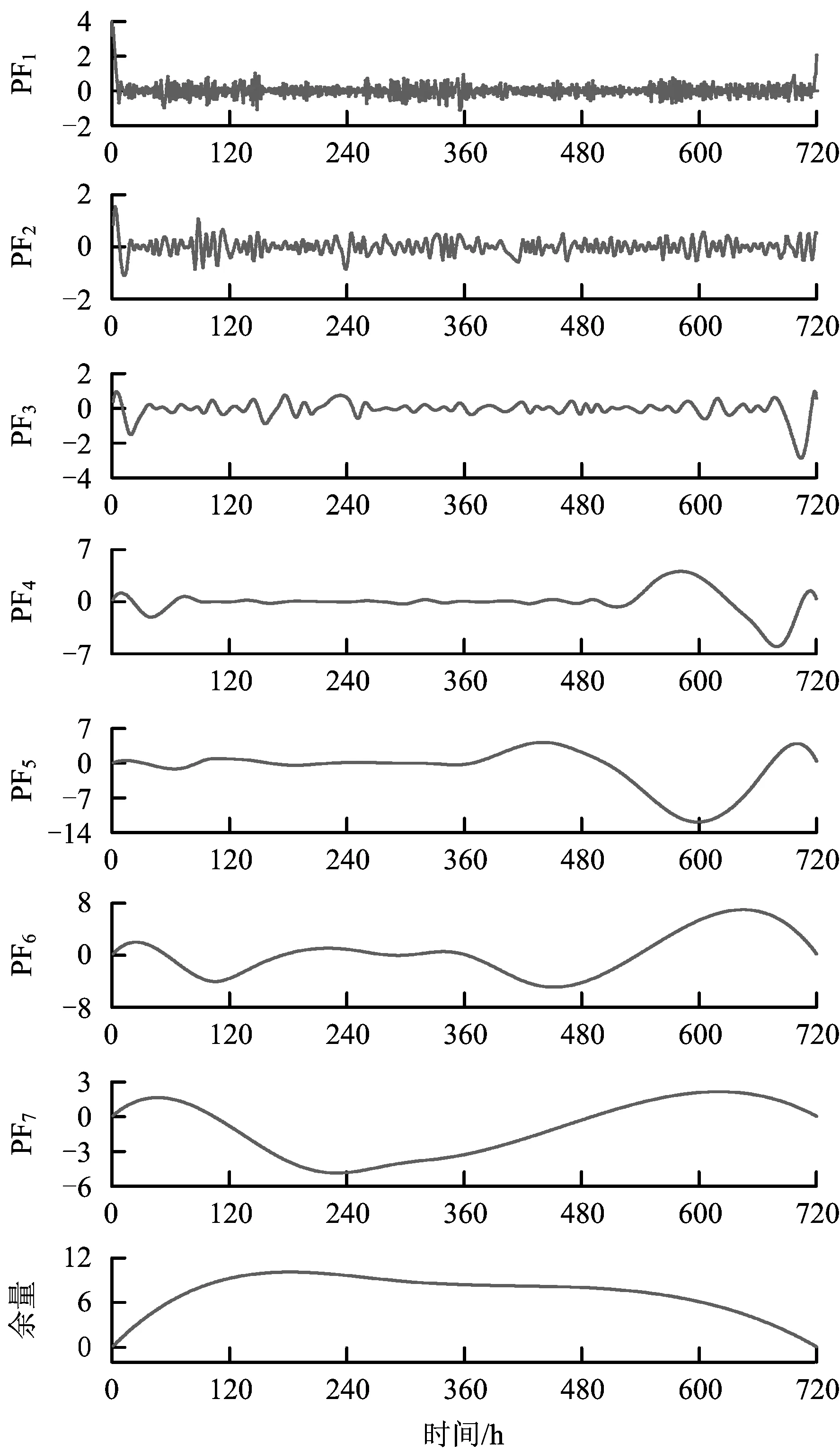
图3　瓦斯涌出量EMD分解Fig.3　EMD decomposition of gas emission quantity

由图3可知，原始瓦斯涌出量时变序列经过EMD分解后得到7个IMF分量和1个余量，原始序列在分解过程中，分量的振动周期逐渐加长，其震荡剧烈程度逐渐平缓。余量的振动周期超出样本空间，振幅平均值与瓦平均斯涌出量一致均为5.51 m3/min。经EMD后，瓦斯涌出的非平稳本质特征由IMF分量与余量共同刻画。工作面瓦斯涌出量由于受到煤层原始瓦斯含量、煤层埋深、厚度等内在因素影响，表现出一定的趋势性，即瓦斯涌出的相对均衡性；同时由于外在因素影响，如：采煤工艺、通风方式、监测数据误差或噪声等，使得瓦斯涌出量表现出不同振动频率。

利用伪近邻法和最小互信息法确定相空间的嵌入维数m和相空间时延τ，对各分量和余量进行空间重构，各相空间参数如表1所示，然后利用重构后的时变序列进行训练和预测，将各预测值进行等权求和，获得最终预测结果。

现取监测样本序列前673 h瓦斯涌出量对MFOA-ELM网络模型进行训练，利用训练后的模型对后48 h瓦斯涌出量进行预测，模型最终预测结果如图4所示。为验证EMD算法处理非平稳时变序列的优越性，利用MFOA-ELM模型对相空间重构后的原始时变序列进行预测，预测结果如图5所示，并将预测结果与EMD-MFOA-ELM模型的最终预测结果进行对比分析。

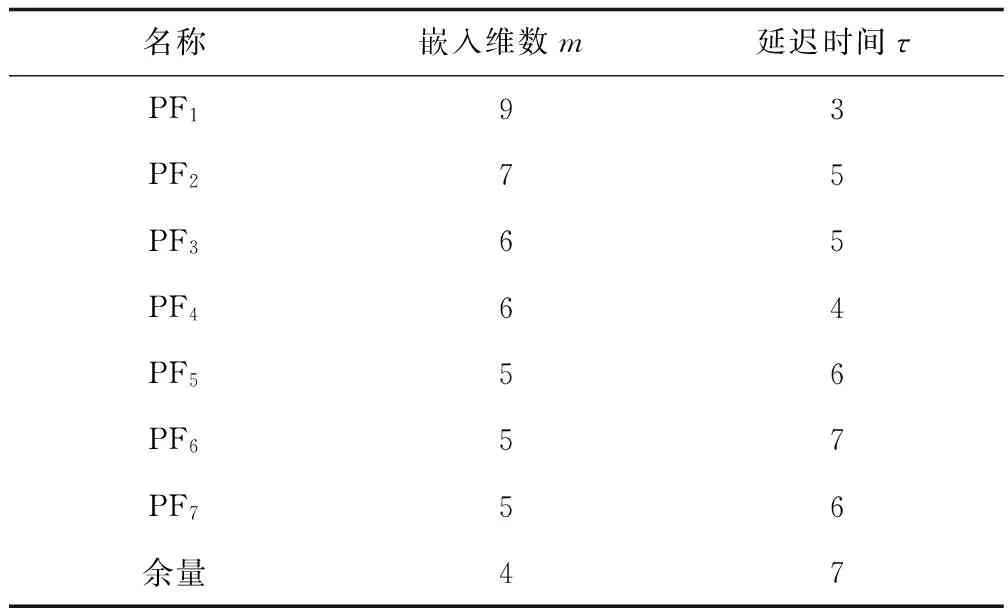
表1　相空间重构参数Table 1　Reconstruction parameters of phase space

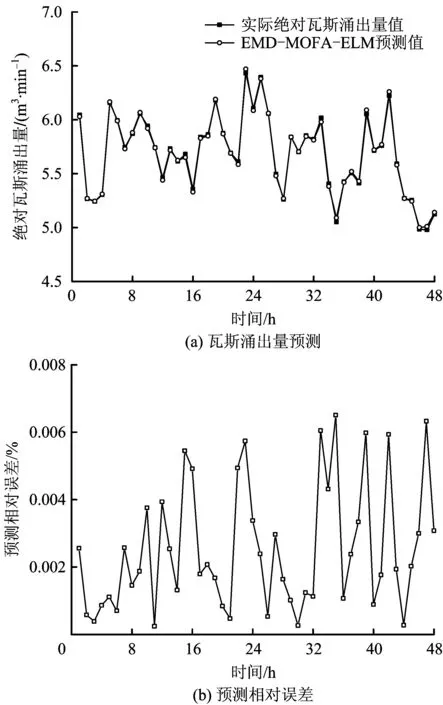
图4　基于EMD-MFOA-ELM模型的瓦斯涌出量预测Fig.4　Prediction of gas emission based on EMD-MFOA-ELM model

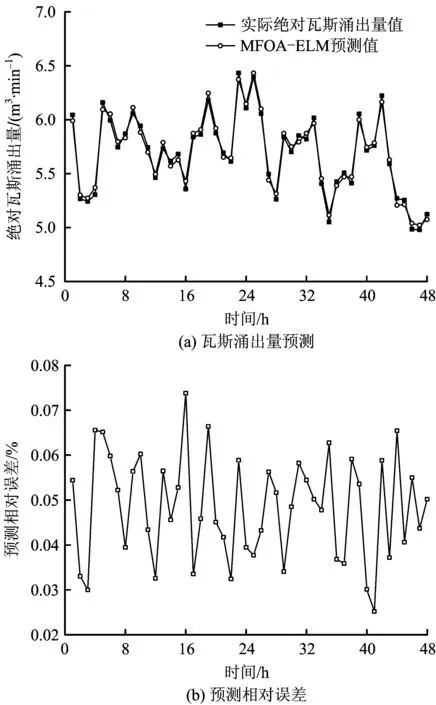
图5　基于MFOA-ELM模型的瓦斯涌出量预测Fig.5　Prediction of gas emission based on EMD-MFOA model

由图4和图5可知，MFOA-ELM模型在随机变化的非平稳信号预测方面误差较大；利用EMD将工作面绝对瓦斯涌出量分解为8个平稳序列，然后再运用MFOA-ELM模型对分量预测，预测精度相对于未经EMD分解模型提高了近10倍，预测结果与实际涌出量值表现出一致性，EMD-MFOA-ELM模型对非平稳时变序列工作面绝对瓦斯涌出量列预测具有很好地适用性。

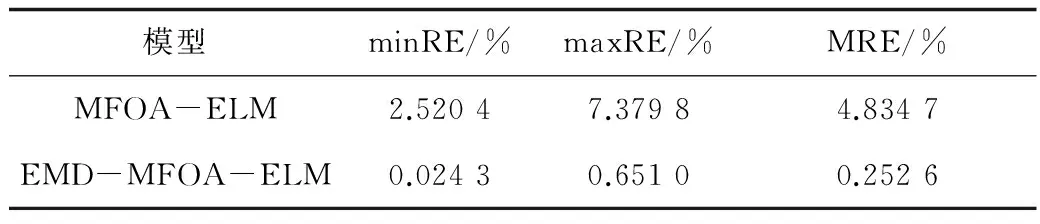
表2　2种模型误差分析Table 2　Error analysis of the two models

为进一步验证模型的优越性，将预测相对误差作为评价指标对预测模型进行分析。由表2可知，未进行EMD分解的MFOA-ELM模型预测相对误差为2.520 4%～7.379 8%，平均相对误差为4.834 7%，在实际工程应用中基本能满足精度要求，但EMD-MFOA-ELM模型预测的相对误差为0.024 3%～0.651 0%，而平均相对误差仅为0.252 6%。由此可知，EMD从时序样本自身挖据数据隐含规律，通过将时变序列分解成IMF分量和余量来刻画数据的本质结构，实现非平稳序列的平稳化，使得模型预测精度得到进一步提高，对非平稳时变序列有很好地适用性。

4　结论

1) 监测数据自身携带诱使瓦斯涌出量变化的大量信息，EMD分解能有效反映出监测数据间的本质结构，各IMF和余量能进一步刻画瓦斯涌出量的非平稳本质结构，能有针对性地建立更准确的预测模型。

2) 利用EMD方法将原始瓦斯涌出量时变序列分解成7个IMF分量和1个余量，对每个分量和余量分别进行相空间重构，然后建立MFOA-ELM预测模型进行预测，根据等权重求和原则，将各预测值进行叠加得到最终预测结果，采用相对误差为模型评价指标，对模型的预测结果进行检验。基于EMD-MFOA-ELM模型的预测结果与实际值基本吻合具有很好一致性，平均相对误差仅为0.2526%，明显小于未经EMD分解模型。

3) 基于EMD-MFOA-ELM的时变预测模能够深层次地诠释瓦斯涌出量的非平稳性，更加全面地挖掘出瓦斯涌出量变化规律，降低非平稳性对预测结果的影响，实现了瓦斯涌出精准和稳定地动态预测，为分析矿井瓦斯涌出非平稳特性提供了理论依据，具有重要研究价值。

[1]吕伏, 梁冰, 孙维吉,等. 基于主成分回归分析法的回采工作面瓦斯涌出量预测[J]. 煤炭学报, 2012, 37(1):113-116.

LYU Fu, LIANG Bing, SUN Weiji, et al. Gas emission quantity prediction of working face based on principal component regression analysis method[J]. Journal of China Coal Society, 2012, 37(1):113-116.

[2]皮子坤, 贾宝山, 贾廷贵，等. 煤与瓦斯突出预测综合指标F临界值研究[J]. 中国安全生产科学技术, 2015, 11(9):38-44.

PIi Zikun, JIA Baoshan, JIA Tinggui，et al. Study on critical value of comprehensive index F for coal and gas outburst prediction[J]. Journal of Safety Science and Technology, 2015, 11(9):38-44.

[3]付华, 谢森, 徐耀松,等. 基于MPSO-WLS-SVM的矿井瓦斯涌出量预测模型研究[J]. 中国安全科学学报, 2013, 23(5):56-61.

FU Hua, XIE Sen, XU Yaosong, et al. Study on MPSO-WLS-SVM-based mine gas emission prediction model [J]. China Safety Science Journal, 2013, 23(5):56-61.

[4]单亚锋, 侯福营, 付华,等. 基于改进极端学习机的混沌时间序列瓦斯涌出量预测[J]. 中国安全科学学报, 2012, 22(12):58-63.

SHAN Yafeng, HOU Fuying, FU Hua, et al. Prediction of chaotic time series of gas emission based on improved extreme learning machine[J]. China Safety Science Journal, 2012, 22(12):58-63.

[5]樊保龙, 白春华, 李建平. 基于LMD-SVM的采煤工作面瓦斯涌出量预测[J]. 采矿与安全工程学报, 2013, 30(6):946-952.

FAN Baolong, BAI Chunhua, LI Jianping. Forecasting model of coalface gas emission based on LMD-SVM method[J]. Journal of Mining & Safety Engineering, 2013, 30(6):946-952.

[6]李胜, 韩永亮, 李军文. 回采工作面瓦斯涌出量耦合预测模型研究[J]. 计算机工程与应用, 2015, 51(16):1-5.

LI Sheng, HAN Yongliang, LI Junwen. Research on coupling prediction model for gas emission quantity of working face[J]. Computer Engineering and Applications, 2015, 51(16):1-5.

[7]刘俊娥, 安凤平, 林大超,等. 采煤工作面瓦斯涌出量的固有模态SVM建模预测[J]. 系统工程理论与实践, 2013, 33(2):505-511.

LIU June, AN Fengping, LIN Dachao, et al. Prediction of gas emission from coalface by intrinsic model SVM modeling [J]. Systems Engineering-Theory&Practice, 2013, 33(2):505-511.

[8]时培明, 丁雪娟, 李庚,等. 一种EMD改进方法及其在旋转机械故障诊断中的应用[J]. 振动与冲击, 2013, 32(4):185-190.

SHI Peiming, DING Xuejun, LIGeng, et al. An improved method of EMD and its applications in rotating machinery fault diagnosis[J]. Journal of Vibration and Shock, 2013, 32(4):185-190.

[9]张淑清, 翟欣沛, 董璇,等. EMD及Duffing振子在小电流系统故障选线方法中的应用[J]. 中国电机工程学报, 2013, 33(10):161-167.

ZHANG Shuqing, ZHAI Xinpei, DONG Xuan, et al. Application of EMD and duffing oscillator to fault line detection in Un-effectively grounded system[J]. Proceedings of the CSEE, 2013, 33(10):161-167.

[10]付华, 李海霞, 卢万杰,等. 一种改进的极限学习机煤与瓦斯突出预测模型[J]. 传感技术学报, 2016, 29(1):69-74.

FU Hua, LI Haixia, LU Wanjie, et al. A prediction model of coal and gas outburst based on improved extreme learning machine. Chinese Journal of Sensors and Actuators, 2016, 29(1):69-74.

[11]朱志洁,张宏伟. 基于GA-ELM的冲击地压危险性预测研究[J]. 中国安全生产科学技术,2014,10(8):46-51.

ZHU Zhijie, ZHANG Hongwei. Study on hazard prediction of rock burst based on GA-ELM[J]. Journal of Safety Science and Technology, 2014, 10(8):46-51.

[12]李彬, 李贻斌. 基于ELM学习算法的混沌时间序列预测[J]. 天津大学学报, 2011,44(8):701-704.

LI Bin, LI Yibin. Chaotic time series prediction based on ELM learning algorithm[J]. Journal of Tianjin University, 2011,44(8):701-704.

[13]皮子坤, 贾宝山, 贾廷贵,等. 煤矿瓦斯涌出量动态预测的PCA-MFOA-GRNN模型及应用[J]. 传感技术学报, 2015, 28(11):1676-1681.

PI Zikun, JIA Baoshan, JIANG Yangui, et al. Coal mine gas emission dynamic prediction of PCA-MFOA-GRNN model and its application[J]. Chinese Journal of Sensors and Actuators, 2015, 28(11):1676-1681.

[14]张宏伟, 朱志洁, 霍丙杰,等. 基于改进的FOA-SVM导水裂隙带高度预测研究[J]. 中国安全科学学报, 2013, 23(10):9-14.

ZHANG Hongwei, ZHU Zhijie, HUO Bingjie, et al. Water Flowing Fractured Zone Height Prediction Based on Improved FOA-SVM[J]. China Safety Science Journal, 2013, 23(10):9-14.

[15]李胜, 韩永亮. 基于MFOA-SVR露天矿边坡变形量预测研究[J]. 中国安全生产科学技术, 2015, 11(1):11-16.

LI Sheng, HAN Yongliang. Research on forecasting of slope deformation in open-pit mine based on MFOA-SVR[J]. Journal of Safety Science and Technology, 2015, 11(1):11-16.