非马尔科夫环境下两体及多体纠缠研究

汪 明，张建松

（华东交通大学理学院，江西 南昌 330013）

非马尔科夫环境下两体及多体纠缠研究

汪 明，张建松

（华东交通大学理学院，江西 南昌 330013）

利用hierarchy方程研究了非旋波非马尔科夫近似下三量子比特系统在同一热库下两体及多体纠缠的演化。研究表明，可以通过改变系统与环境相互作用强度以及热库的非马尔科夫性质调整两体及多体纠缠，对实现非马尔科夫环境下基于多体系统的量子信息过程有较大帮助。

非旋波近似；非马尔科夫近似；量子纠缠；量子比特；hierarchy方程

量子纠缠是存在于复合量子体系中的一种量子现象，它是将态的叠加原理作用于复合量子体系，从而得到一个自然的结果。 对复合量子体系中一个子体系进行测量，它的状态将会发生塌缩，同时，另外的一个或几个子体系状态也会发生相应的变化，这种现象称为量子纠缠。近些年来，量子信息作为一门新型交叉学科得到了快速发展，而量子纠缠也逐渐成为量子信息学科中最重要的物理资源之一。量子纠缠在量子隐形传态、量子纠错、量子存储、量子编码、量子计算等方面得到了很大运用[1]。所以，量子纠缠将是越来越重要的研究课题。

实际的量子系统多少都会受到环境的影响，所以事实上所有的量子系统都是开放的。环境对开放的量子系统动力学演化过程具有很大的影响，根据对量子系统的不同影响过程，可以把这种影响过程分为两种情况，分别是马尔科夫和非马尔科夫过程。 在马尔科夫过程中，环境可以看作一个单向流动的通道，当量子系统中的信息与能量流入到环境中时，信息和能量将很快被耗散，它们不再反馈到量子系统中去；因此将马尔科夫过程称为没有记忆功能的并且是单向流通的过程。而在非马尔科夫过程中，当量子系统中的能量和信息流入到环境中后，随着时间的推移，环境将会反馈部分能量和信息到量子系统中，也就是说这个时候环境有了一定的记忆功能。

在量子纠缠动力学演化的过程中，系统和热库是混合的，并且需要一个微扰，这样能够通过求迹得出热库自由部分的程度，这个微扰被称为波恩近似。此外，如果热库的时间尺度远小于系统时间尺度，这即是马尔科夫近似。为避免上述两种近似的一种高效方法由Tanimura等提出[2-4]，建立了一系列的hierarchical方程[5]，该方程包含系统和热库相互作用的所有阶次。 在系统和环境的耦合强度太强而不能使用波恩近似，或者热库的时间规格等同于系统时间规格而不能采用马尔科夫近似时，必须采用hierarchy方程。 本文使用hierarchy方程研究3个量子比特和同一热库的相互作用模型，这种方法被广泛应用到研究退相干自由子空间[5]和双向纠缠动力学[6]中。一个显著特点是基于旋波近似下的稳定纠缠度，它仅仅取决于初始态和退相干自由态的重叠部分，与系统和热库的耦合度无关[6]。但是当考虑非旋波近似项时，对于某些系统和热库耦合度，双激发过程将发生，稳定的纠缠将消失。

1 Hierarchy方程

考虑两量子比特，体系的哈密顿量可以表示为

式中：HS是系统的哈密顿量；HB是热库的哈密顿量；Hint为相互作用哈密顿量，并且有

式中：w1a，w2a为系数；V为系统算符 （不妨令V=a1σ1x＋a2σ2x）；a1，a2为系数；wk为频率；gk为量子比特和热库中第k个模式的耦合系数。

在相互作用绘景下，系统的密度算符可以表示为

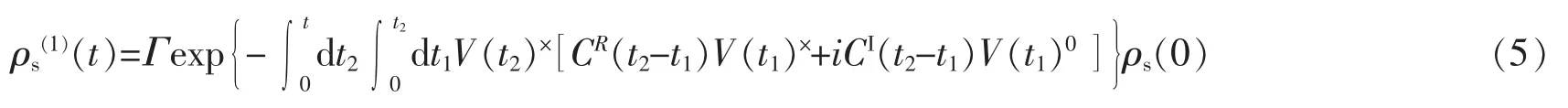
式中：Γ为时阶序列算符。热库时间相关函数可以表示为

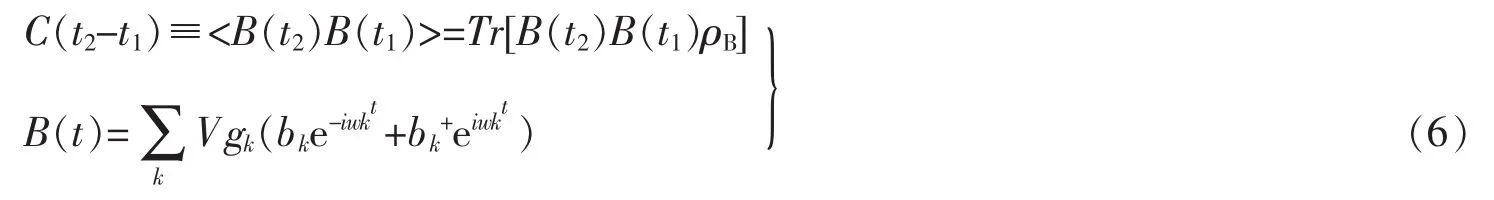
其实部和虚部分别为：CR（t2-t1），CI（t2-t1）。

并且定义以下关系式：

体系的初始态可以表示为

式中：ZB为配分函数。现在考虑量子比特与单模腔相互作用，频率为w0。由于腔存在缺陷，单模展开并且量子腔耦合光谱变成洛伦兹类型，可以表示为

其中：λ反映了系统和热库的耦合强度；γ是腔模扩展的宽度。在T＝0时，腔的初始态为一真空态⊗k┃0k〉，时间相关函数变为

纵观当前林政资源管理中生态建设的现状来看，虽然较以往取得一定的成效，但是其中仍旧存在的一定不足之处，所呈现的效果并不十分如人意。具体来说，林政资源管理中生态建设存在的问题具体表现在以下几个方面：

那么实部和虚部可以表示为

初始条件有：Fk（0）=0，再引入以下表达式：

那么式（14））可以重新表达为

式（21）即为hierarchy方程。

2.1 有相互作用的三量子比特中任意两量子比特的纠缠行为[7]

设系统的初始波函数为 |ψS（0）≥|0>1⊗|0>2⊗|0>3，系统的哈密顿量写为

量子比特算符为

其中：η为三量子比特的相互作用系数，w1a=w2a=w3a=w0=1，a1=a2=a3=1，λ=0.1w0。由于这3个量子比特的性质是完全相同的，所以研究两量子比特的纠缠行为可以用任意两量子比特的纠缠行为来表示。

改变相互作用系数η，得到任意两量子比特随时间的纠缠行为，如图1，从η=0.6，η=1两幅图可以看出，当η较小时，两量子比特之间的纠缠振荡受到抑制，并且系统处于纠缠死亡的时间消失。而从η=2图可以看出，当η较大时，纠缠振荡又逐渐加强。当增大γ时，纠缠振荡会受到抑制，纠缠度也减小。在非旋波近似下，系统和热库的耦合强度对量子比特的纠缠行为有决定性的影响。

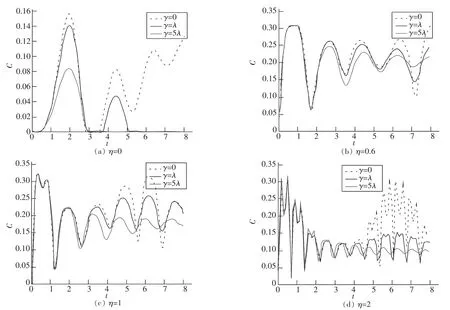
图1 任意两量子比特随时间的纠缠度Fig.1 Time-dependentent entanglement of any two qubits

2.2 有相互作用的三量子比特间真实多体纠缠特性[8]

若系统算符可以写成ρ=p1ρA|BC+p2ρB|AC+p3ρC|AB的形式，则称系统为可分离态。 若不能写成上述形式，则称系统为真实多体纠缠态。A，B，C为3个子系统。纠缠度

系统的初始波函数为 |ψS（0）>=|0>1⊗ |0>2⊗ |0>3，这时的初始条件与2.1节一样，哈密顿量也一样。 这3个量子比特的性质是完全相同的，但这时要计算的是总的真实纠缠度。同样的，改变相互作用系数η，得到总的量子比特随时间变化的纠缠行为，如图2所示。 从图中可以看出，随着相互作用系数η的增大，总的纠缠度在提高，纠缠振荡在加强。当增大γ时，纠缠振荡会受到抑制，三量子稳定后的总纠缠度也会减小，并且当γ超过某一极限值时，将不会出现这个稳定值，非马尔科夫过程也将消失。也就是说可以通过调节γ的值，实现非马尔科夫过程与马尔科夫过程之间的转换。

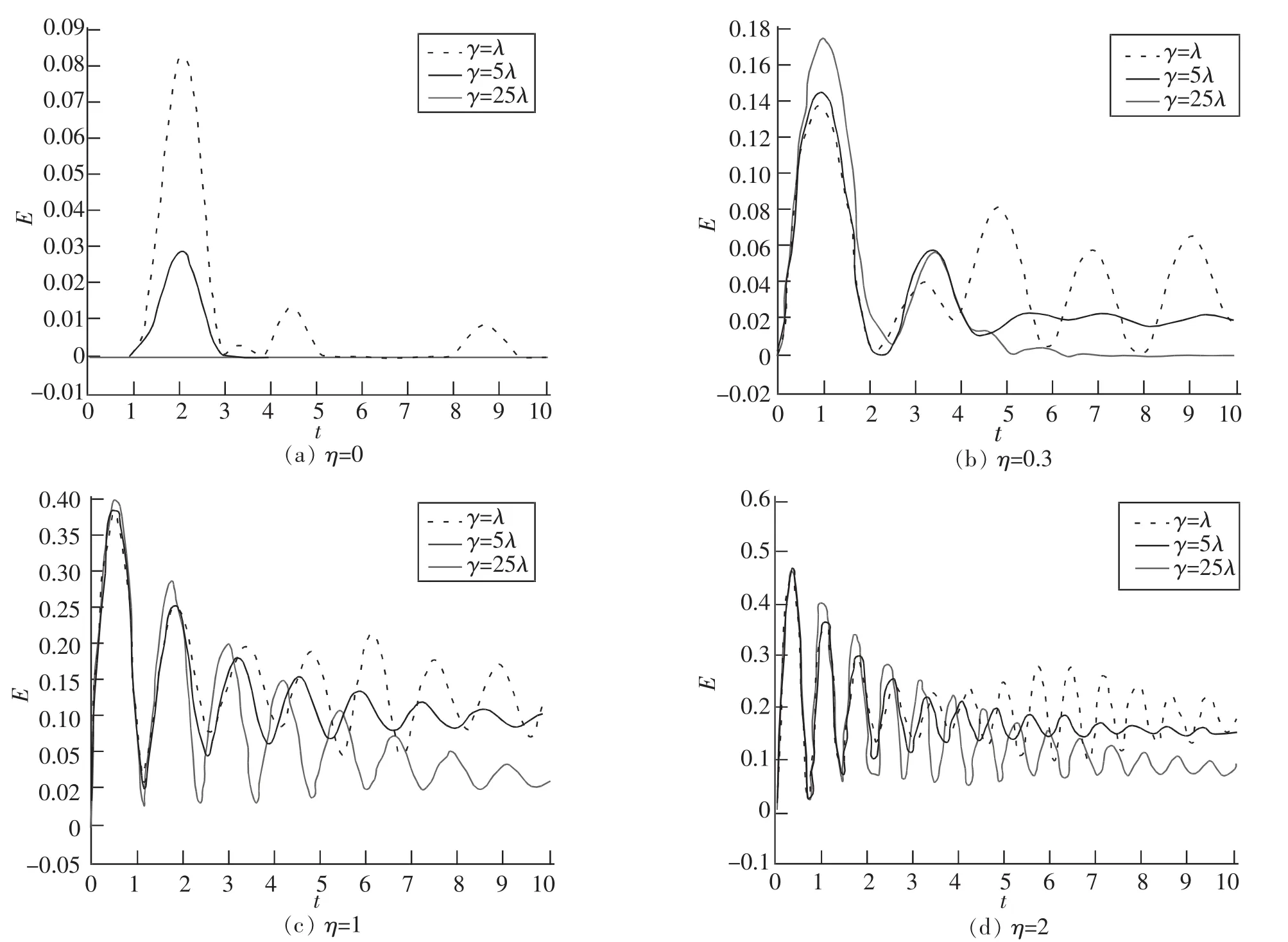
图2 三量子比特的总纠缠度Fig.2 Total entanglement of three qubits

3 结论

利用hierarchy方程研究了非马尔科夫环境下量子系统的功力学演化，通过求解一系列常微分方程组得到系统任意时刻的密度矩阵，以此为基础研究了热库对两体及多体纠缠的影响。研究表明，在马尔科夫环境下由于量子特性一旦扩散到环境中就不可逆转的丢失，因此量子纠缠会快速消亡，此时无法进行量子计算过程。然而如果将量子系统放置于非马尔科夫环境中，两体量子纠缠的振荡随着非马尔科夫性质的增强得到增强，两体量子纠缠的突然死亡现象也将消失。接着，基于部分转置的概念研究真实的量子三体纠缠，随着非马尔科夫特性的增强，三体真实纠缠也会产生振荡。

以上性质可以从物理角度进行解释，量子系统与环境相互作用必然伴随着量子特性从量子系统到环境的扩散，对于马尔科夫环境，由于量子特性一旦丢失无法恢复，此时量子纠缠会消失殆尽。应当指出，对于非马尔科夫环境，情况会截然不同，由于丢失的部分量子特性可以通过非马尔科夫环境返回到量子系统，因此量子纠缠将会得到部分恢复，此时依旧可以实现量子计算。本文利用hierarchy方程定量揭示了非马尔科夫环境对量子计算过程的积极意义，对在实验室中实现量子计算有一定的借鉴意义。

[1]MA NIELSEN，ISAAC L CHUANG.Quantum computation and quantum information[M].北京：清华大学出版社，2005：72-128.

[2]WERLANG T，DODONOV A V，DUZZIONI E I，et al.Rabi model beyond the rotating wave approximation：generation of photons from vacuum through decoherence[J].Phys Rev A，2008，78：753-805.

[3]TANIMURA Y，KUBO R.Time evolution of a quantum system in contact with a nearly Gaussian-Markoffian noise bath[J].Journal of the Physical Society of Japan，1989，58（1）：101-114.

[4]ISHIZAKI A，TANIMURA Y.Quantum dynamics of system strongly coupled to low-temperature colored noise bath：reduced hierarchy equations approach[J].Journal of the Physical Society of Japan，2005，74（12）：3131-3134.

[5]TANIMURA Y.Stochastic Liouville，Langevin，Fokker－Planck，and master equation approaches to quantum dissipative systems[J]. Journal of the Physical Society of Japan，2006，75（8）：82-84.

[6]ZANARDI P，RASETTI M.Noiseless quantum codes[J].Physical Review Letters，1997，79（17）：33－36.

[7]ZHANG J S，HUANG Z Y，CHEN A X.Bipartite and multipartite correlations of coupled qubits in a non-markovian environment：hierarchy equation method[J].International Journal of Quantum Information，2013，11（6）：135－135.

[8]唐智慧.基于纠缠态的量子对话设计研究[D].南昌：华东交通大学，2015：12－15.

Study of Bipartite and Multipartite Entanglement Without Rotatingwave and Markovian Approximations

Wang Ming，Zhang Jiansong
（School of Science，East China Jiaotong University，Nanchang 330013，China）

Hierarchy equation was adopted to study the evolution of bipartite and multipartite entanglement of three qubits system without rotating-wave and Markovian approximations.The study shows that the entanglement of bipartite and multipartite can be controlled by the interaction of the system and the environment or the non-Markovian property of bath,which is very useful to realize quantum information process under the non-Markovian environment based on the multipartite system.

non-rotating wave approximation；non-Markovian approximation；quantum entanglement；qubit；hierarchy equation

O431.2

A

1005-0523（2017）02-0112-06

（责任编辑 刘棉玲）

2016－09－27

国家自然科学基金项目（11565013）；江西省科学研究基金项目（20151BAB202020）

汪明（1988—），男，硕士研究生，研究方向为量子信息。

张建松（1981—），男，副教授，博士，研究方向为量子光学和量子信息。