地铁运营对沿线不同基础型式建筑物的振动影响

于凯文，金 浩

（同济大学道路与交通工程教育部重点实验室，上海 201804）

地铁运营对沿线不同基础型式建筑物的振动影响

于凯文，金 浩

（同济大学道路与交通工程教育部重点实验室，上海 201804）

为研究地铁运营时，不同基础型式建筑物的振动响应规律，对独立基础、条形基础和桩基的五层框架结构，进行了1～80 Hz频段的竖向（水平向）振动位移、速度以及加速度分析，得出：① 三种基础型式，建筑物一层地面中心的竖向振动位移、速度和加速度普遍大于水平向振动位移、速度和加速度。②独立基础和条形基础，随着楼层的增大，水平向振动加速度增大。桩基水平向振动加速度从第1层到第4层，无明显规律。第5层的水平向振动加速度普遍大于前4层的振动加速度。竖向振动加速度随楼层的增大，都没有明显规律。

地铁；建筑振动；基础；数值模拟

地铁极大地缓解了城市的交通拥堵，但同时也引发了一系列环境振动问题。国内外已有不少媒体，就地铁振动造成的环境问题进行报道，譬如：地铁振动会导致沿线居民情绪异常烦躁，精密仪器不能正常使用[1]，建筑结构产生振动及裂缝。列车、钢轨相互作用产生的振动波，经过轨道→隧道→地层，最终传播到沿线建筑结构。因此，有必要研究地铁运营对沿线建筑结构的振动影响规律。

目前，对地铁运营引起建筑结构振动的分析，主要采用数值模拟和现场实测的方法。比如：洪俊青等[2]建立了土层-建筑物二维有限元模型，采用Newmark隐式积分法，以时域最大竖向振动加速度为评价指标，得出：建筑物各楼层振动响应水平基本相同，上部楼层的振动仅比下部楼层振动有小幅上升。陈士海等[3]利用ANSYS/LS-DYNA建立了20层框架结构受地铁振动影响的模型，以振动加速度峰值作为评价指标，得出：3个方向的振动加速度峰值的最大值都出现在第一层，但没有表现出随着楼层增大而增大的现象。闫维明等[4，5]对地铁平台上多层住宅楼的竖向振动进行了现场实测，以振动加速度振级作为分析参数，得出：多层建筑物竖向振动基本表现为整体振动，以频率低于70 Hz的振动为主，楼层间信号的放大主要集中在10～30 Hz频段。第5层以下振动逐层增强，第5层以上振动基本无变化。毕伟[6]等对地铁沿线某一砌体建筑物振动响应进行现场实测，以竖向振动加速度幅值为评价指标，得出：竖向加速度幅值在低频激励下随楼层增高而增加，在高频激励下随楼层增高而衰减。凌育洪等[7，8]以Z向振级作为评价指标，同样得出了Z向振级逐层增大的结论。

鉴于分析指标不同，部分文献之间的结论存在偏差。另外，建筑类型多样（结构，层数，平面布局，基础，等等），也导致现有分析结果的不完善。目前，尚没有针对建筑结构基础型式的文献。基于此，以北京地区地质条件为例，拟对采用独立基础、条形基础和桩基的建筑结构进行振动分析。

1 基础型式

以北京地铁某盾构隧道区间地质条件为背景，假定分析的建筑物为五层框架结构。层高3 m，楼板厚0.2 m，楼高16.2 m。建筑物垂直隧道中心线方向的长度为8 m。共有2个开间，每个开间3.7 m，墙厚0.2 m。由于建立的隧道-地层-建筑物模型为平面应变模型，因此不考虑建筑物沿隧道中心线方向的长度。建筑物具体尺寸如图1所示。

图1 建筑物详细尺寸（单位：m）Fig.1 Specific size of the building(m)

在平面模型中无法区别条形基础和筏形基础，因此不考虑筏形基础的影响。通过设计，独立基础埋深1.6 m，宽2 m，下部柱宽为 0.4 m。独立基础布置方式如图2所示，具体尺寸如图3所示。

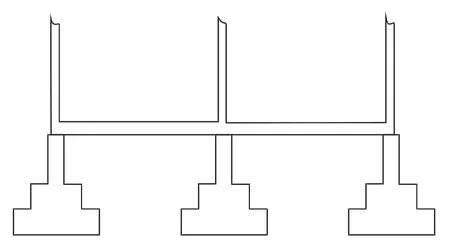
图2 采用独立基础的建筑物Fig.2 Building with independent foundation

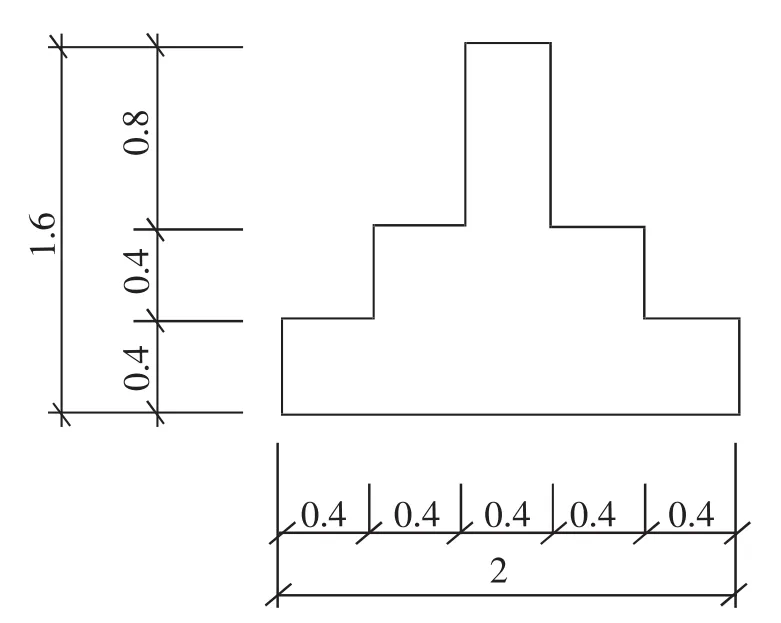
图3 独立基础详细尺寸（单位：m）Fig.3 Specific size of independent foundation（m）

设计的条形基础：埋深1.6 m，整体宽9.8 m，下部柱宽0.4 m，具体尺寸如图4所示。

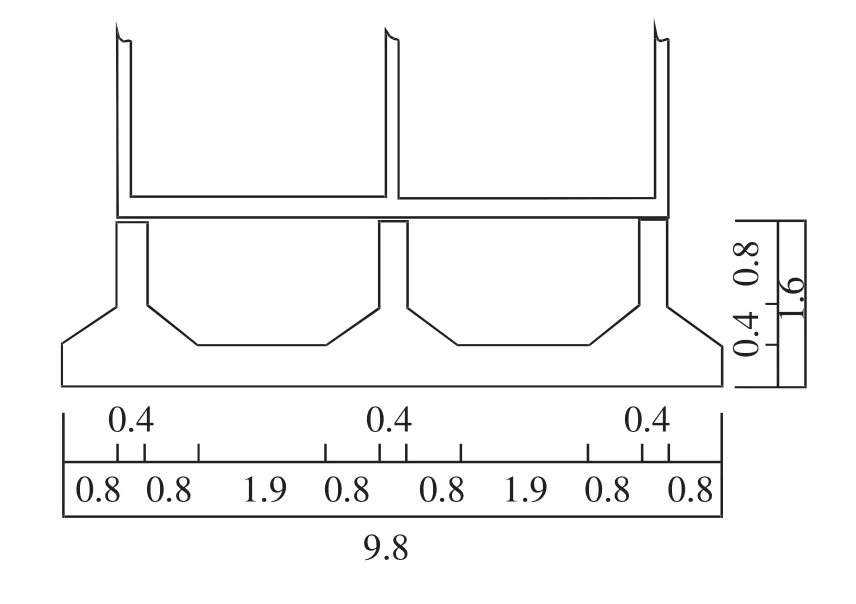
图4 条形基础详细尺寸（单位：m）Fig.4 Specific size of strip foundation（m）

设计的桩基：桩长20.33 m，承台厚0.4 m，承台宽0.8 m，详细尺寸如图5所示。

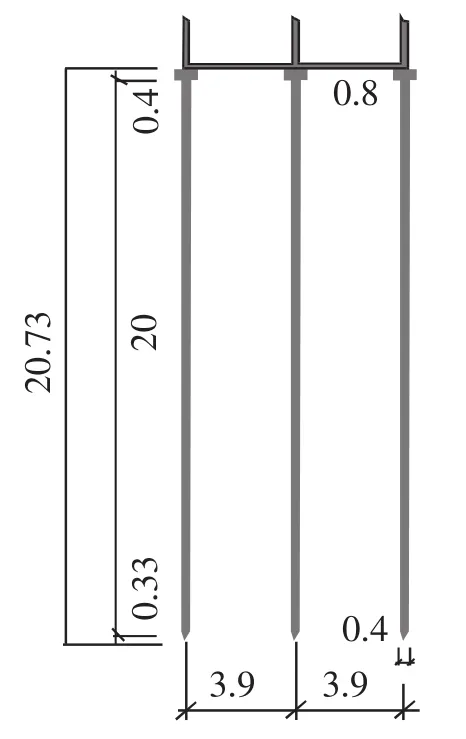
图5 桩基详细尺寸（单位：m）Fig.5 Specific size of pile foundation（m）

2 有限元模型

紧邻建筑物的隧道为圆形盾构隧道，隧道外半径3 m，内半径2.7 m，壁厚0.3 m。隧道埋深15 m，左右线相距10 m。右线隧道距离建筑物约10 m，如图6所示。

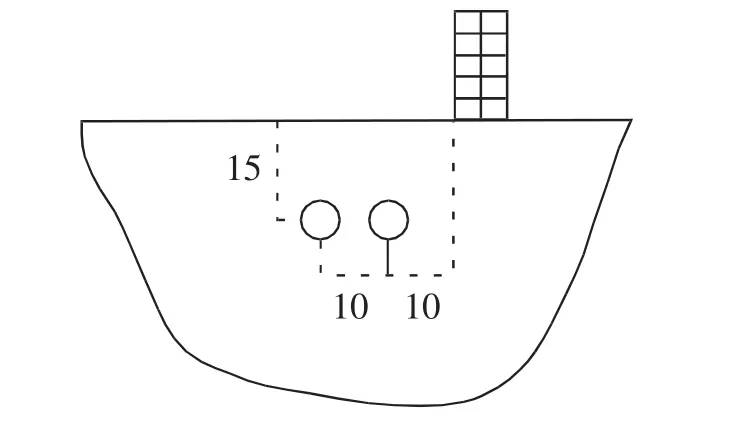
图6 隧道和建筑结构的相对位置（单位：m）Fig.6 Relative position of tunnel and building（m）

根据地质勘查资料，对不同类型的土层进行了合并。假定土层分为3层，如图6所示。计算参数如表 1所示。

表1 土层材料参数Tab.1 Soil parameter

采用有限元软件ABAQUS进行建模分析，根据有限元建模的一些文献结论[9]，模型的截断边界距振源不应小于介质的最大半波长，即

式中：CS为剪切波速，可以从表1查阅各土层的剪切波速。本次研究的最小频率采用1 Hz，即fmin=1。经公式计算得λ为147 m，则取模型的计算尺寸：为竖向165 m，水平向310 m。模型的四边采用固定约束，不考虑波反射的问题。

在振动的拾取点附近，为了准确捕捉振动效应，单元尺度不应大于相应土层中最小波长的1/6，即

本次分析频率的上界为200 Hz，即fmax=200 Hz。因此，各土层网格的最大尺寸要求为：土层1不大于0.15 m，土层2不大于0.2 m，土层3不大于0.245 m。

建筑物混凝土的质量密度2 350 kg/m3，弹性模量30 GPa，泊松比0.2。基础（独立基础、条形基础以及桩基）的质量密度2 350 kg/m3，弹性模量32.5 GPa，泊松比0.2。盾构隧道的质量密度2 350 kg/m3，弹性模量36 Gpa，泊松比0.2。

3 计算方法

模型采用中心差分法进行动力计算。以单自由度为例，对中心差分法进行简述：

假定：整个动力计算过程，时间不长不变，记为△ti=△t。则，速度和加速度的中心差分近似为

体系的运动方程为

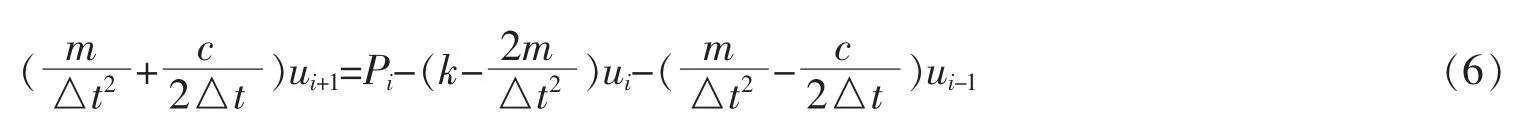
据此，就可以根据ti及以前时刻的运动，得到ti+1时刻的运动。

4 列车荷载

列车荷载可以通过经验公式、实测、车轨模型、数定列车荷载等多种方法实现。本文采用数定列车荷载[10]，如下：

首先，将现场实测的轨道振动加速度波形分解为一系列不同频率的谐波，公式如下：

对钢轨竖向振动加速度波形进行离散取样：

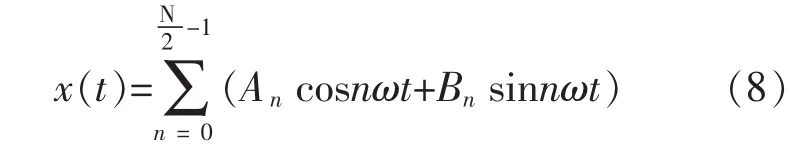
其次，将地铁列车简化为二系弹簧-质量系统模型，如图7所示。其中，m3为1/8车体质量，m2为1/4转向架质量，m1为1/2轮对质量，z0为钢轨竖向位移，z1为轮对竖向位移，z2为转向架竖向位移，z3为车体竖向位移，k1为轮对弹簧系数，c1为轮对阻尼系数，k2为转向架弹簧系数，c2为转向架阻尼系数。

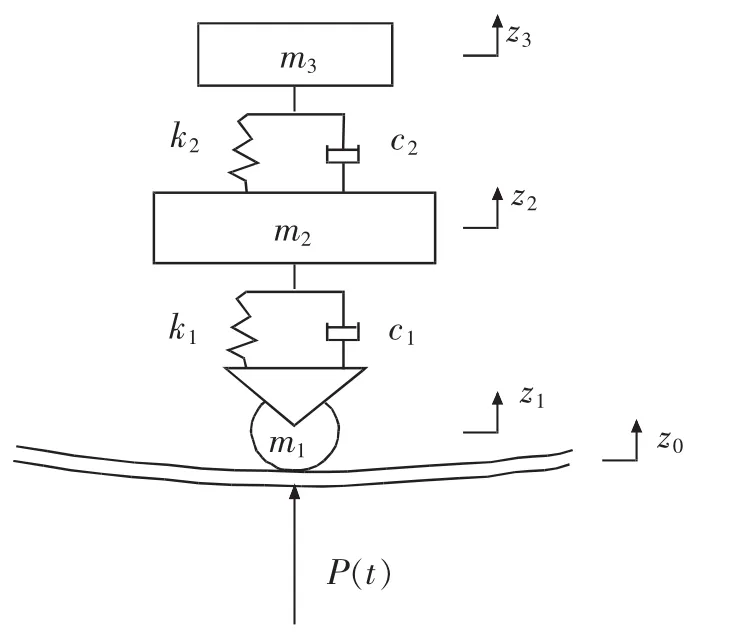
图7 地铁列车竖向振动简化模型Fig.7 Simplified model of metro vertical vibration

对m2和m3进行动力分析，建立如下方程：

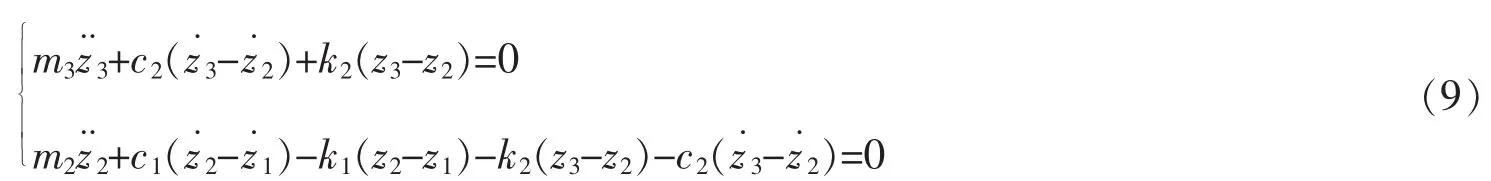
可得轮轨间相互作用力为

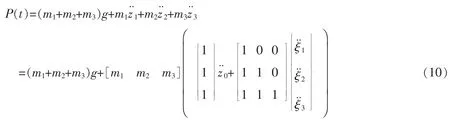
式中：ξ1＝z1－z0，ξ2＝z2－z1，ξ3＝z3－z2

进一步，沿纵向均匀分布的列车线荷载可按下式计算：

式中：K为修正系数；n为每节车厢的转向架数；M为列车车厢数，L为列车长度。

根据表2提供的物理参数以及n=2，M=6。通过实测北京某地铁线的钢轨振动加速度时程，得到模拟列车振动荷载的时程曲线，如图8所示。

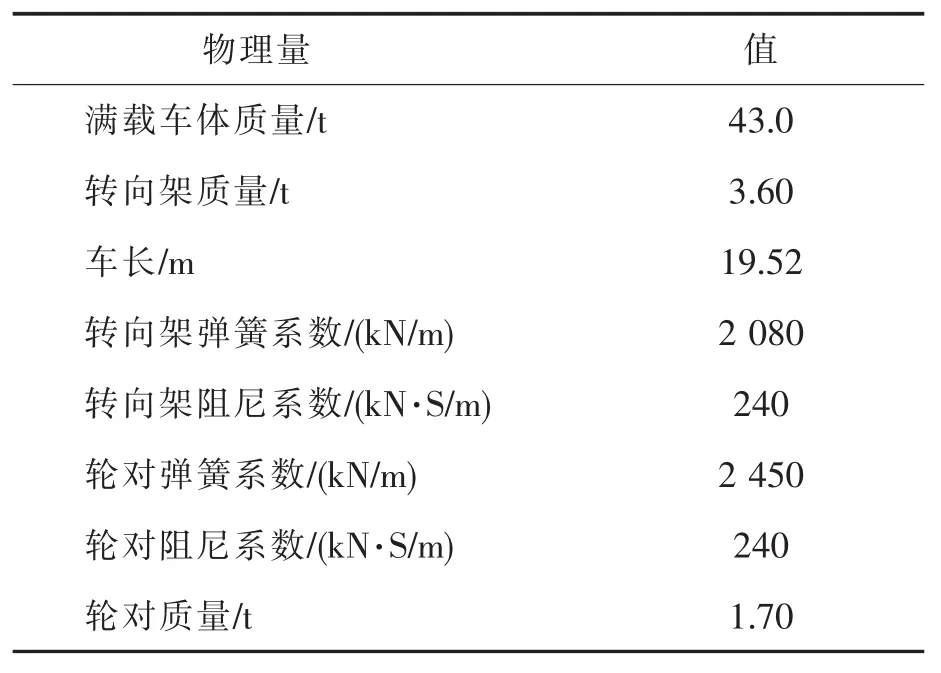
表2 北京某地铁线运营车辆参数Tab.2 Train parameters of a metro line in Beijing

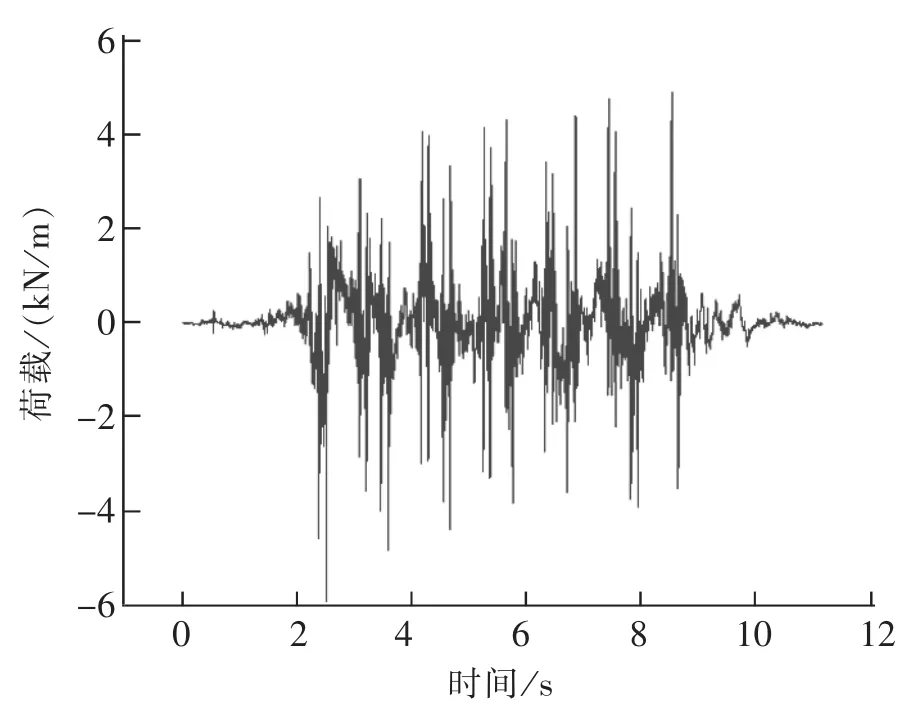
图8 列车荷载Fig.8 Train load

5 基础型式的影响

将建筑物一层地面中心定为拾振点，采样频率设置为312.5 Hz。得到采用不同基础型式时，建筑物1层地面中心的竖向（水平向）位移、竖向（水平向）速度和竖向（水平向）加速度时程。本文以1～80 Hz[11]为分析频段，利用Matlab软件对计算得到的时程进行快速傅里叶变换等处理，得到建筑物1层地面中心竖向（水平向）位移频谱、竖向（水平向）速度频谱以及竖向（水平向）加速度频谱。进一步，利用得到的频谱数据，通过频域处理方法，得到对应的1/3倍频程，如图9～图11所示。

从图9可以得出：① 竖向振动位移级随着频率的增大而降低。水平向振动位移级没有这一规律；② 在1～40 Hz的低频区，3种基础型式的水平向振动位移级接近，没有多大区别。在频率大于40 Hz的频段，采用桩基的建筑物水平向振动位移级迅速增大。相比之下，独立基础和条形基础二者变化不大；③ 对比图9（a）和图9（b），很明显，竖向振动位移级普遍大于水平向振动位移级。

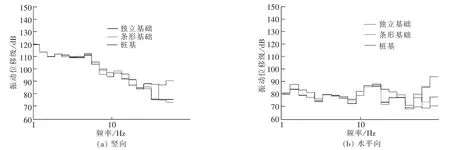
图9 振动位移级Fig.9 Vibration displacement level

从图10可以得出：①在1～80 Hz频段，竖向振动速度级普遍大于水平向振动速度级；②水平向振动速度级随着频率的增大而增大。竖向振动速度级没有表现出这种规律；③在40 Hz以上频段，采用桩基的建筑物水平向振动速度级增加明显。

从图11可以得出：① 采用桩基的建筑物，竖向振动加速度级略大于水平向振动加速度级；② 整体来说，桩基对应的竖向和水平向振动加速度比独立基础和条形基础对应的振动加速度大；③ 独立基础和条形基础，在1～10 Hz的低频区，水平向振动加速度级很小。说明低频区水平向振动加速度的隔离，建筑物宜采用独立基础和条形基础。

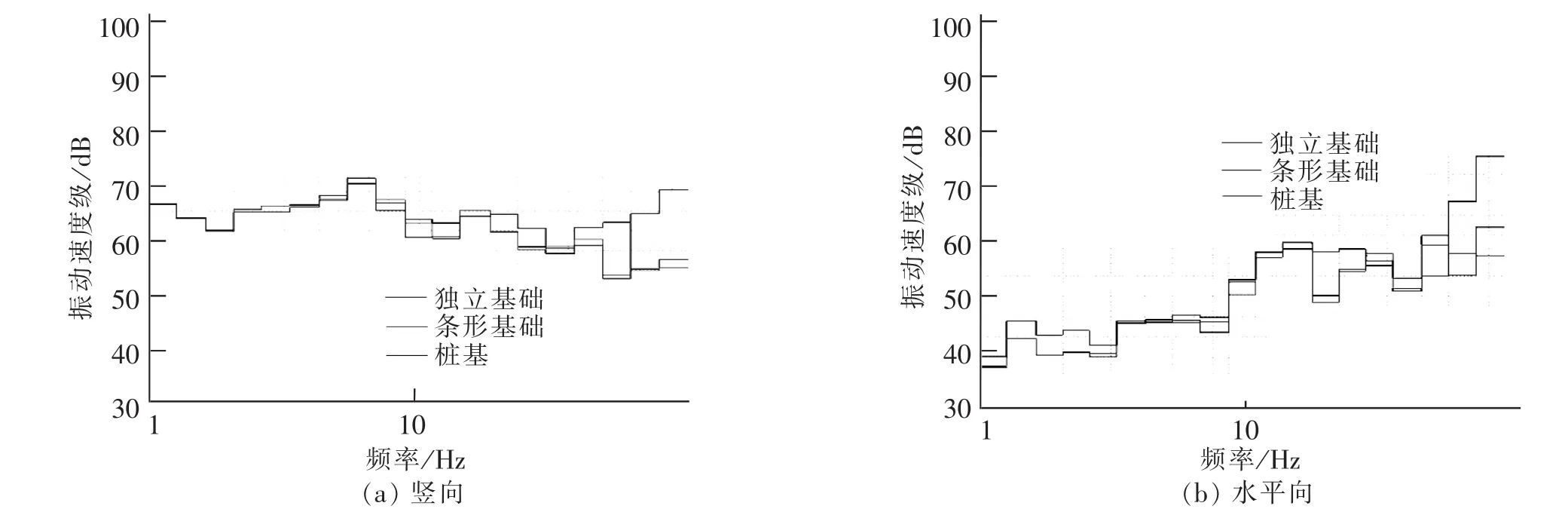
图10 振动速度级Fig.10 Vibration velocity level

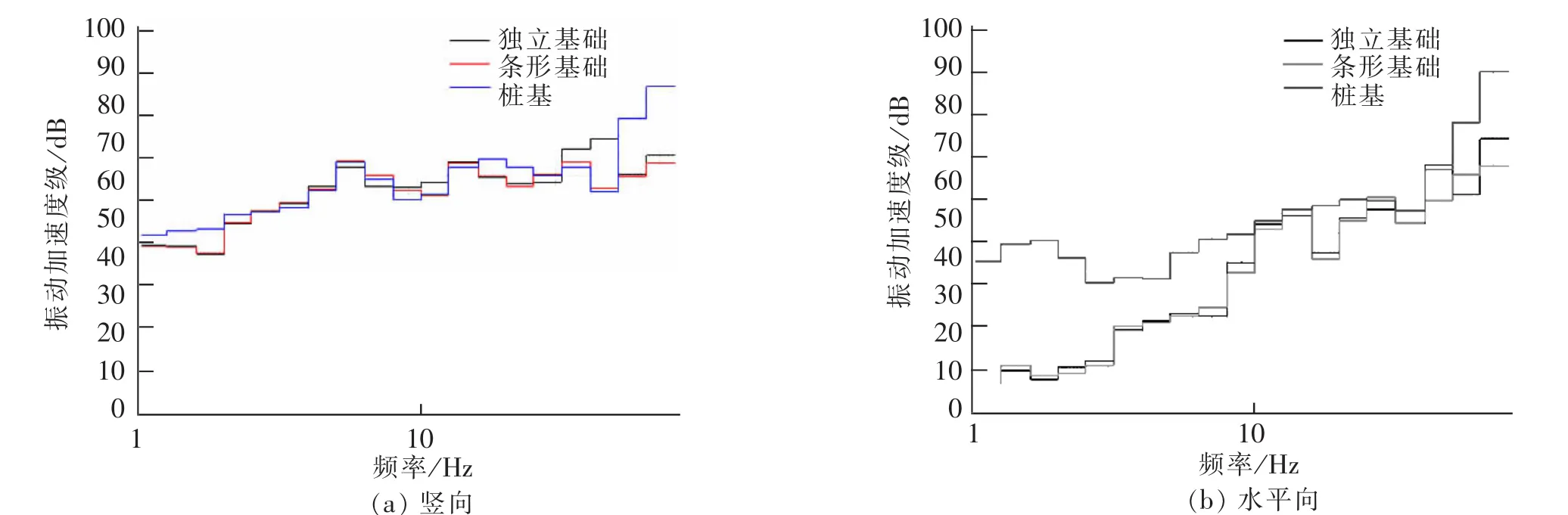
图11 振动加速度级Fig.11 Vibration acceleration level

6 楼层振动分布规律

目前，国内标准多采用振动加速度作为分析量。因此，本文重点分析了竖向和水平向振动加速度随楼层的分布规律。

采用独立基础的建筑物，振动加速度随楼层变化规律，如图12所示。得出：①不管是竖向还是水平向，振动加速度都随着频率的增大而增大；② 随着楼层的增加，水平向振动加速度表现出明显的增大趋势。竖向振动加速度随楼层增加，无明显规律。

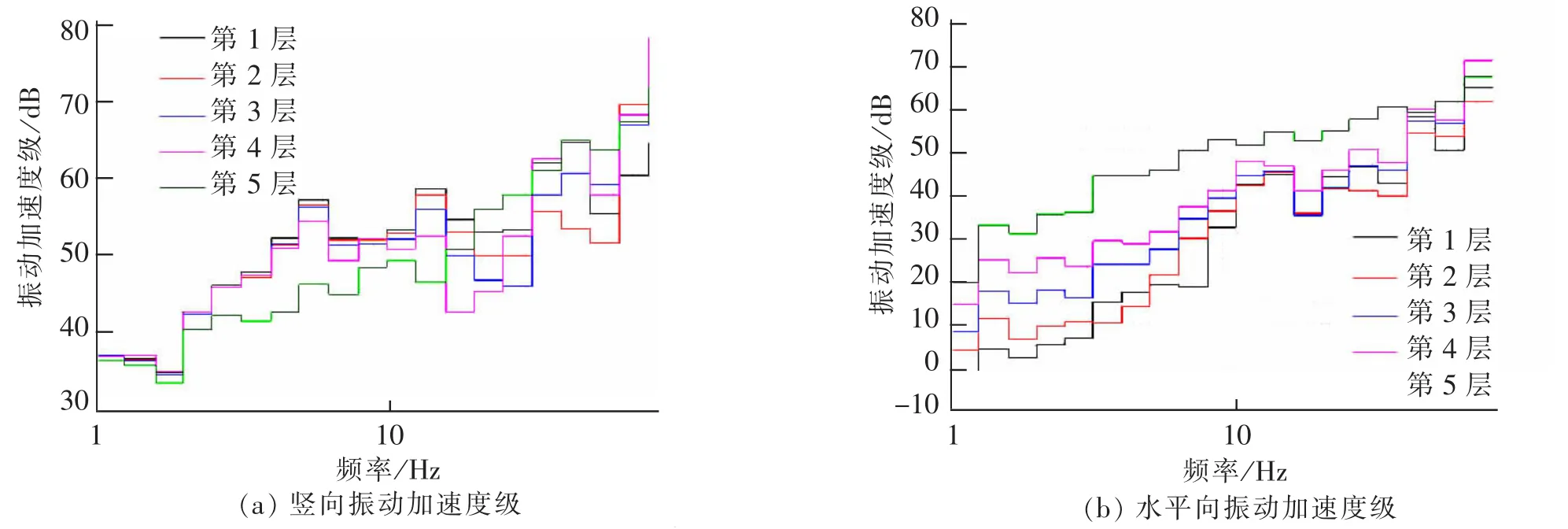
图12 独立基础Fig.12 Independent foundation

采用条形基础的建筑物，振动加速度随楼层变化规律，如图13所示。得出：条形基础和独立基础具有类似的规律。水平向振动加速度随着楼层的增加而增大，规律明显。竖向振动加速度无明显趋势。

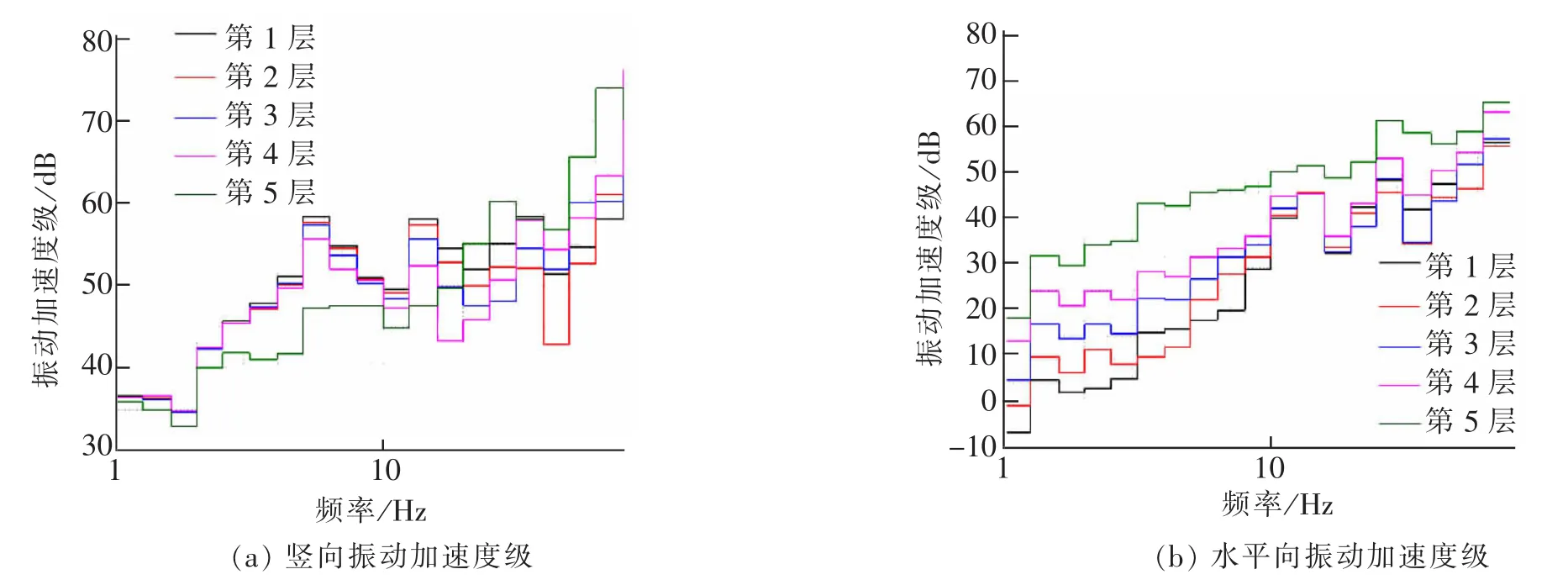
图13 条形基础Fig.13 Strip foundation

采用桩基的建筑物，振动加速度随楼层变化规律如图14所示。得出：①水平向振动加速度从第1层到第4层，无明显规律。第5层的水平向振动加速度普遍大于前4层的振动加速度。② 同样，竖向振动加速度随着楼层的增加，并未表现出特定的规律。

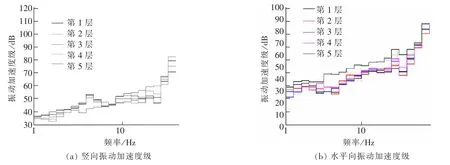
图14 桩基Fig.14 Pile foundation

7 结论

本文分析了地铁运营下，某建筑物在采用不同基础型式（独立基础、条形基础和桩基）时，竖向和水平向振动位移、速度以及加速度的规律。得出：

1）不管是独立基础，还是条形基础或桩基，建筑物1层地面中心的竖向振动位移、速度和加速度普遍大于水平向振动位移、速度和加速度。

2）3种基础型式的建筑物，竖向振动加速度随楼层的增大，都没有明显规律。

3）独立基础和条形基础，随着楼层的增大，水平向振动加速度增大。尤其是低频区，规律明显。桩基水平向振动加速度从第1层到第4层，无明显规律。第5层的水平向振动加速度普遍大于前4层的振动加速度。

4）从建筑物隔振角度来看，独立基础和条形基础的隔振效果接近，且都比桩基好。

参考文献：

[1]马蒙，刘维宁，丁德云，等.地铁列车振动对精密仪器影响的预测研究[J].振动与冲击，2011，30（3）：185-190.

[2]洪俊青，刘伟庆.地铁对周边建筑物振动影响分析[J].振动与冲击，2006，25（4）：142-145.

[3]陈士海，戚桂峰，张子华.轨道交通荷载下高层框架结构的动力响应[J].武汉理工大学学报，2012，34（9）：84-87.

[4]闫维明，张向东，任珉，等.地铁平台上建筑物竖向振动测试与分析[J].北京工业大学学报，2008，34（8）：836-841.

[5]闫维明，张祎，任珉，等.地铁运营诱发振动实测及传播规律[J].北京工业大学学报，2006，32（2）：149-154.

[6]毕伟.地铁列车所致临近建筑物振动预测方法研究[D].北京交通大学，2015：63-66.

[7]凌育洪，吴景壮，马宏伟.地铁引起的振动对框架结构的影响及隔振研究－以某教学楼为例[J].振动与冲击，2015（4）：184-189.

[8]王田友，丁洁民，楼梦麟，等.地铁运行所致建筑物振动的传播规律分析[J].土木工程学报，2009（5）：33-39.

[9]马蒙.基于敏感度的地铁列车振动环境影响预测及动态评价体系研究[D].北京交通大学，2012：103-104.

[10]王祥秋，杨林德，高文华.铁路隧道提速列车振动测试与荷载模拟[J].振动与冲击，2005，24（3）：99-102，107.

[11]中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.机械振动与冲击人体暴露于全身振动的评价第1部分：一般要求[S].2007.

Influence of Metro Operation on Vibration of Buildings with Different Foundations along the Metro Line

Yu Kaiwen，Jin Hao
（Key Laboratory of Road and Traffic Engineering of the Ministry of Education,Tongji University,Shanghai 201804,China）

In order to study building vibration with different foundations induced by subway operation,a fivestory building with the independent foundation or the strip foundation or the pile foundation was modeled.The displacement,the velocity and the acceleration of the floor in the vertical and the horizontal direction ranging from 1～80Hz were analyzed.The results showed that:(1)The displacement,the velocity and the acceleration of the first floor in the vertical direction are larger than those in the horizontal direction for all foundations;(2)The value of the acceleration in the horizontal direction is increased from the first floor to the top floor for the independent foundation and the strip foundation.The horizontal acceleration is almost the same from the first floor to the fourth floor for the pile foundation.However,the horizontal acceleration of the fifth is bigger than other floors.The vertical acceleration of different floors has no relationship for all foundations.

metro;building vibration;foundation;numerical simulation

U231

A

1005-0523（2017）02-0037-08

（责任编辑 王建华）

2016－09－20

于凯文（1993—），男，硕士研究生，研究方向为轨道交通系统动力学。

金浩（1986—），男，助理教授，博士，研究方向为轨道振动控制。