基于正交法X形密封圈力学性能研究*

王国荣，伍　伟，李　明，胡　刚

(西南石油大学 机电工程学院，四川 成都 610500)

0　引言

密封性能的优劣是评价机械性能的关键因素。密封失效主要由密封圈的失效造成，容易导致工作介质发生泄漏，可能引发火灾爆炸、人身伤亡等重大事故[1-2]。橡胶密封圈由于其良好的密封性能和低成本被广泛应用于机械、石油、航天等领域。O形和X形密封圈是常用的2种橡胶密封圈，均可用于静密封、动密封及旋转密封，相比于O形密封圈，X形密封圈由于具有在动密封中不易翻滚、所需径向压缩率小、有润滑容腔、摩擦阻力小等优点，逐渐在替代O形密封圈。

目前，许多学者研究了几何参数、材料参数、工作介质、温度等单因素对O形密封圈、Y形密封圈性能的影响，如：Zhi Chen等[3]研究了O形密封圈对机械密封动环端面变形的影响；Zhiguo Zeng等[4]建立了O形密封圈泄露与材料属性之间关系的有限元模型；Meng Zhang等[5]采用有限元方法研究了不同间隙和密封沟槽圆角半径对密封性能的影响；Dian Xin Li等[6]分析了不同油压下O形密封圈带有支撑环前后的密封性能；纪军等[7]利用黏弹性力学和摩擦热分析机理，对FESCO气缸O形密封圈进行了温度场分析；Jing Wen[8]对活塞与油缸之间Y形密封圈往复运动进行热—结构耦合分析了材料硬度和温度对密封接触压力和泄露的影响；田阔等[9]基于热弹性力学以及热应力分析理论分析了压力和温度同时变化时Y形密封圈静密封变形与应力分布；刘占军等[10]对优化的X形变截面密封圈进行了基本的有限元分析；韩传军等[11-12]采用单因素法研究了对X形密封圈静密封和动密封性能的影响。目前，尚未见包含温度在内的各因素组合对X形密封圈密封特性的影响及显著性水平的相关研究。

基于此，采用有限元方法建立了X形密封圈的数值仿真模型，采用多因素正交试验方法研究了预压缩量、介质压力、硬度、温度对星形密封圈静密封及摩擦系数、速度对其往复动密封力学性能的影响。

1　 材料模型

X形密封圈采用的丁腈橡胶(NBR)是1种超弹性材料，也称为Green材料。橡胶具有材料非线性、几何非线性和接触非线性。国内外学者提出了多种用于描述胶类非线性材料的模型[11]，如Neo-Hookean模型、Gent模型、Arruda-Boyce模型、Mooney-Rivilin模型、Ogden模型、Yeoh模型等[13]，其中，Mooney-Rivlin模型是1个比较经典且应用广泛的模型，其应变能函数可表示为：

W=C10(I1-3)+C01(I2-3)

(1)

式中：W为应变能密度；C10，C01为橡胶材料Mooney-Rivlin模型系数；I1，I2分别为第一、第二应变张量不变量。

根据GB/T 528-2009硫化橡胶或热塑性橡胶拉伸应力—应变性能的测定[14]标准，采用长度25 mm，宽度6 mm，厚度为2 mm的Ⅰ型哑铃片状试样，试验严格按照GB/T 528-2009标准执行。3组试样使用如图1所示的微机控制电子万能试验机进行安装试验，计算出3组试验数据的平均值。

图1　微机控制电子万能试验机Fig.1　Microcomputer control electron universal testing machine

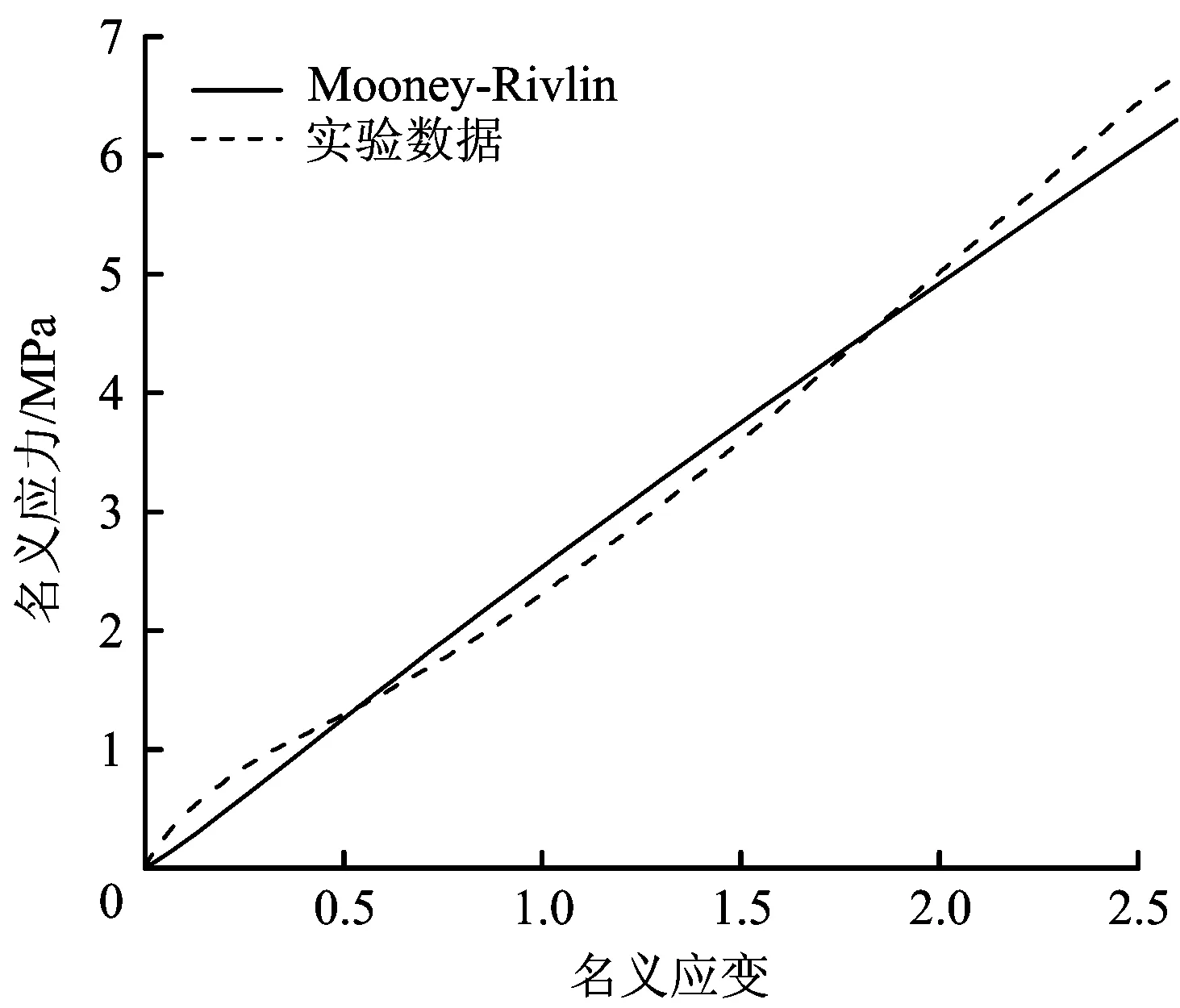
图2　实验数据与Mooney-Rivlin模型拟合Fig. 2　Fitting of experimental data and Mooney-Rivlin model

将橡胶材料应力—应变数据导入ABAQUS软件进行拟合，在拟合过程中选用Mooney-Rivlin模型，拟合曲线如图2所示，最终得到材料的Mooney-Rivlin模型材料参数C10=1.107，C01= -0.764。

2　 有限元模型

2.1　基本假设

由于X形密封圈的力学模型表现出复杂的非线性特征，在进行数值模拟前做如下假设：

1)橡胶材料各向同性。

2)橡胶材料不可压缩。

3)忽略流体介质对密封圈的腐蚀。

4)不考虑橡胶材料黏弹性。

5)密封圈的硬度不随压缩量变化。

2.2　几何模型

结合密封系统的实际结构，建立X形密封圈、沟槽和活塞杆组成的二维轴对称几何模型如图3所示。根据规格标准，选择横截面长度为5.33 mm，内径为43.82 mm，密度ρ1=1 200 kg/m3的X形密封圈，凹槽及活塞杆材料为中碳调制钢，密度ρ2=7 800 kg/m3，弹性模量E=206 GPa，泊松比υ=0.3。

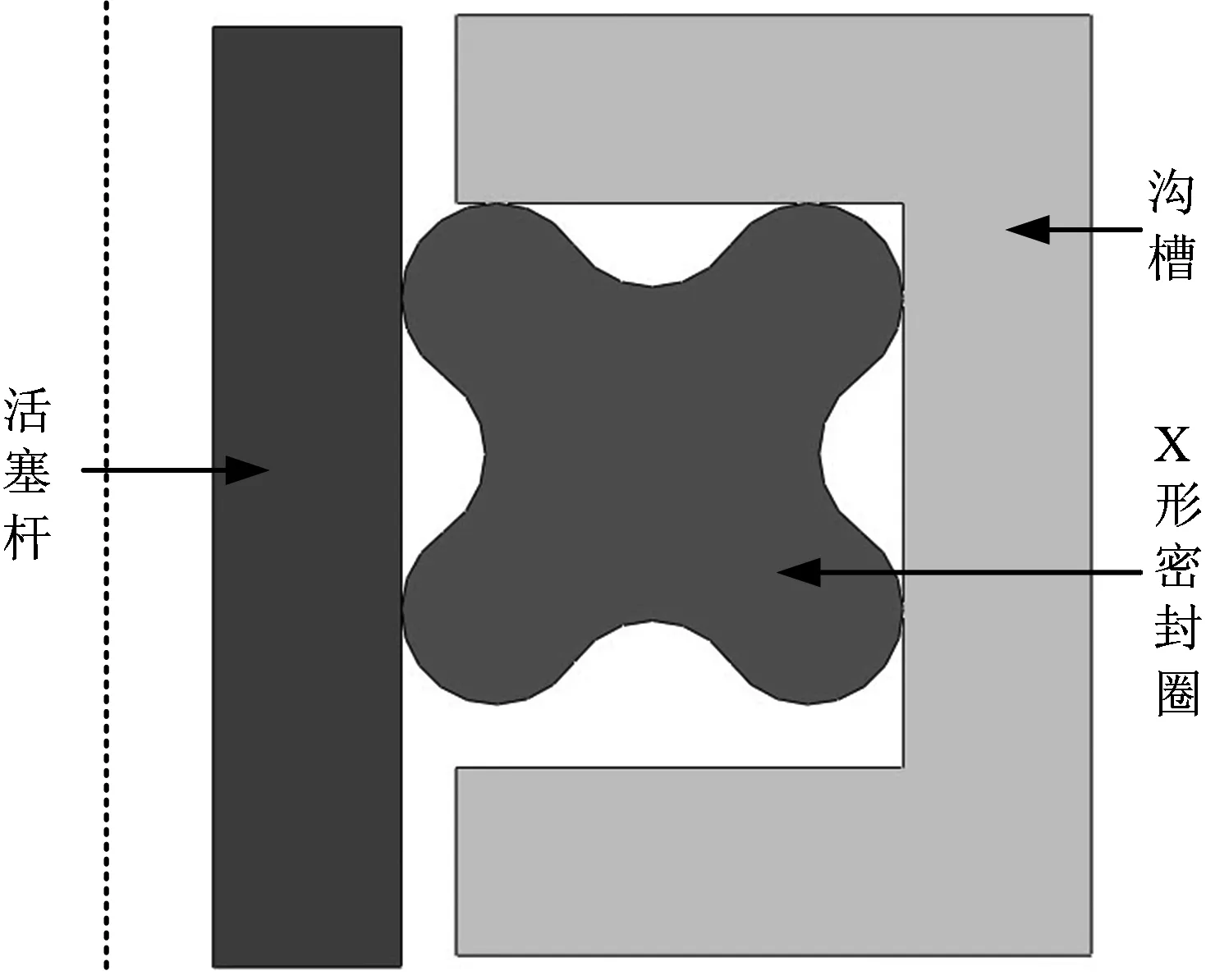
图3　星形密封圈Fig.3　Schematic diagram of X-sealing ring

2.3　仿真模型

以下使用罚单元法，即采用Penalty模型来描述X形密封圈与活塞杆之间的接触问题。建立橡胶密封圈与沟槽、密封圈与活塞杆之间的接触对，其摩擦系数设定为0.3。采用轴对称四边形单元对模型进行网格划分，划分网格之后的有限元模型如图4所示。活塞杆的往复运动是1个双向过程，将其分为外行程(与受油压方向一致)和内行程(与受油压方向相反)过程，加载分为3步：

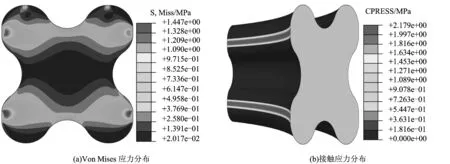
图5 无压力下密封圈应力分布Fig.5　Stress distribution of sealing ring under no-pressure condition

1)预压缩。对凹槽施加径向位移0.2 mm。

2)静密封。对密封圈与流体接触一侧施加2 MPa介质压力，实现静密封。

3)动密封。对活塞杆施加轴向速度，实现动密封。

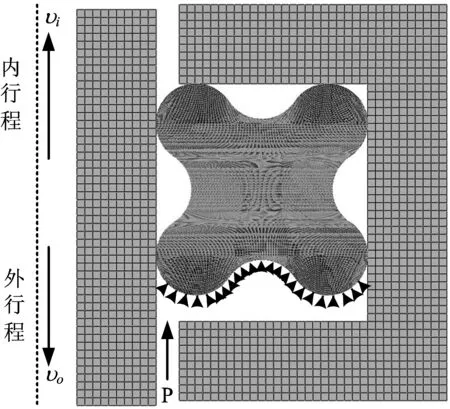
图4　有限元模型Fig.4　Finite element model

2.4　失效准则

为了分析在各种工况下X形密封圈的受力情况，考察密封圈VonMises应力及主密封面上的接触应力分布情况，对X形密封圈进行仿真分析。

VonMises应力是基于剪切应变能的1种等效应力，其值反映了各主应力差值的大小，用来对橡胶密封圈的破损失效和疲劳失效进行评价[15]。Von Mises应力越大，密封圈发生破坏的几率越大。

(2)

式中：σ1，σ2，σ3分别为3个方向上的主应力。

接触应力是指密封圈与其他物体的接触面上的应力大小。接触应力是最能体现密封圈密封性能的指标，当接触应力大于介质压力时，可保证安全，反之，则易发生事故。

3　静密封特性分析

密封圈以0.2 mm的预压缩量安装后，无介质压力和2 MPa介质压力作用下的应力分布云图分别如图5、图6。在无介质压力作用下，X形密封圈的Von Mises应力按截面中心线呈对称分布，最大Von Mises应力为1.447 MPa，且最大应力位置是在密封圈内部，距离接触位置一定距离，与Hertz经典接触力学理论[16]相符，最大接触应力为2.179 MPa。在介质压力为2 MPa的作用下，密封圈再1次被压缩，此时密封圈应力分布更不均匀，其最大Von Mises应力为4.134 MPa，是无压力下的2.86倍。由于活塞杆与密封圈之间形成的接触面为主密封面，所以，文中研究主密封面上的接触应力。该工况下的主密封面上最大接触应力为4.679 MPa，高于2 MPa的介质压力，因而该工况密封是安全的。

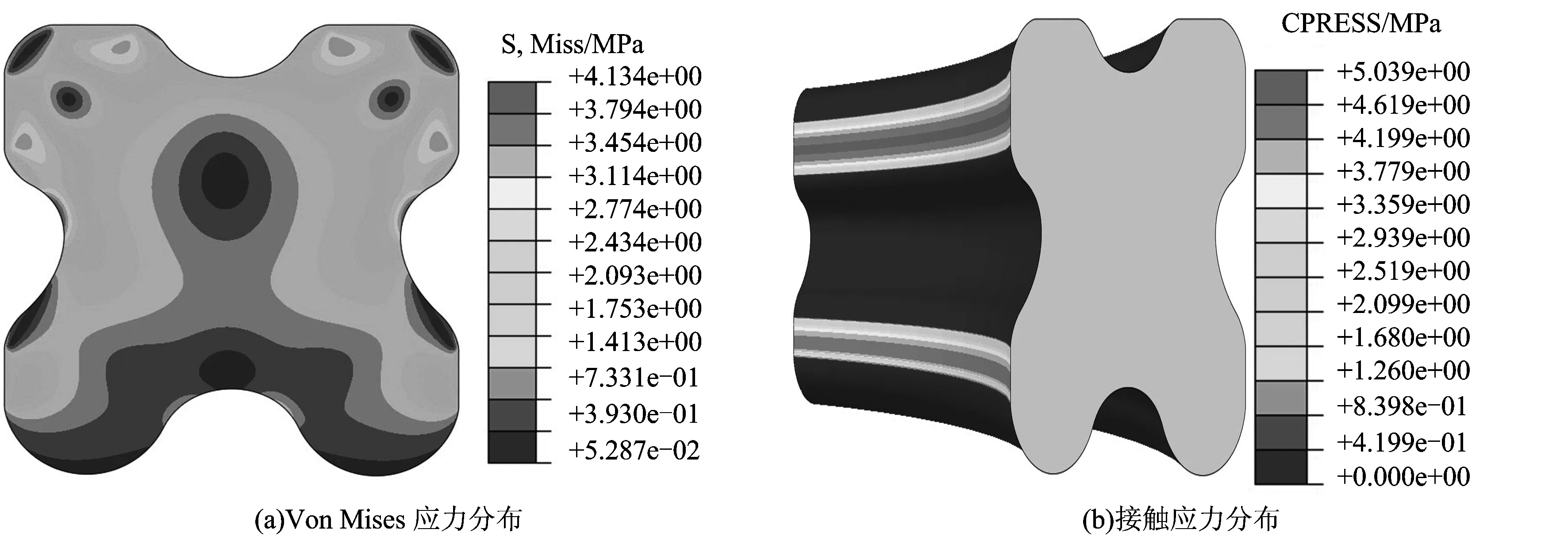
图6　2 MPa压力下密封圈应力分布Fig.6　Stress distribution of sealing ring when P=2 MPa

3.1　正交试验方案设计

以预压缩量、介质压力、硬度、温度为优化因子，各设4个水平，得到4因素4水平正交试验影响因素与水平，如表1所示。

表1　试验设计的因素和水平

正交试验得到的X形密封圈最大Von Mises应力和主密封面上最大接触应力结果如表2所示。

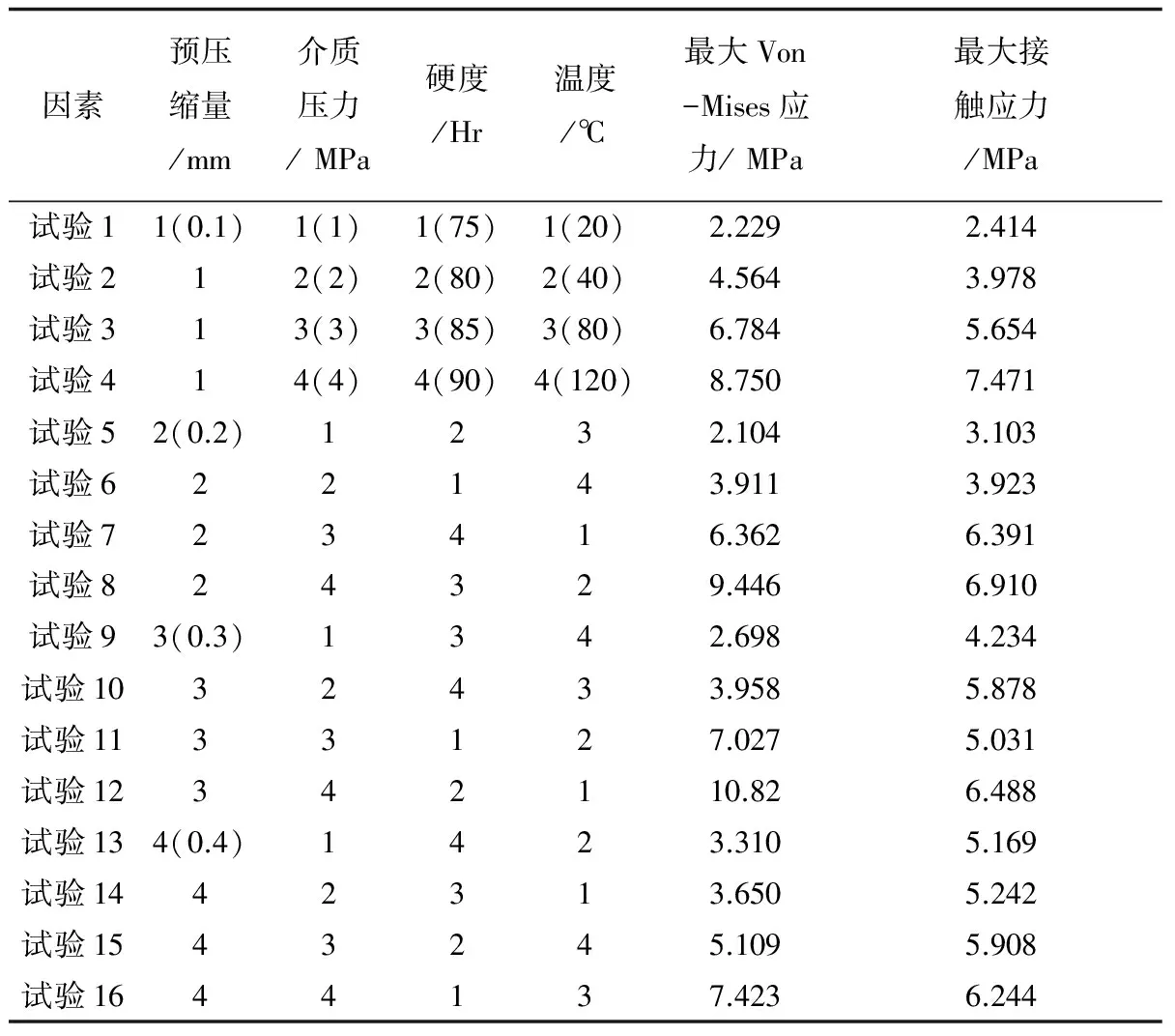
表2　试验设计安排和结果

3.2　参数显著性分析

通过极差分析计算得到不同因素水平的密封圈2种应力的均值与极差值分别如表3、表4所示。表中K1，K2，K3，K4分别表示水平1、水平2、水平3、水平4的水平试验结果总和；k1，k2，k3，k4分别表示水平1、水平2、水平3、水平4的水平试验结果平均值。

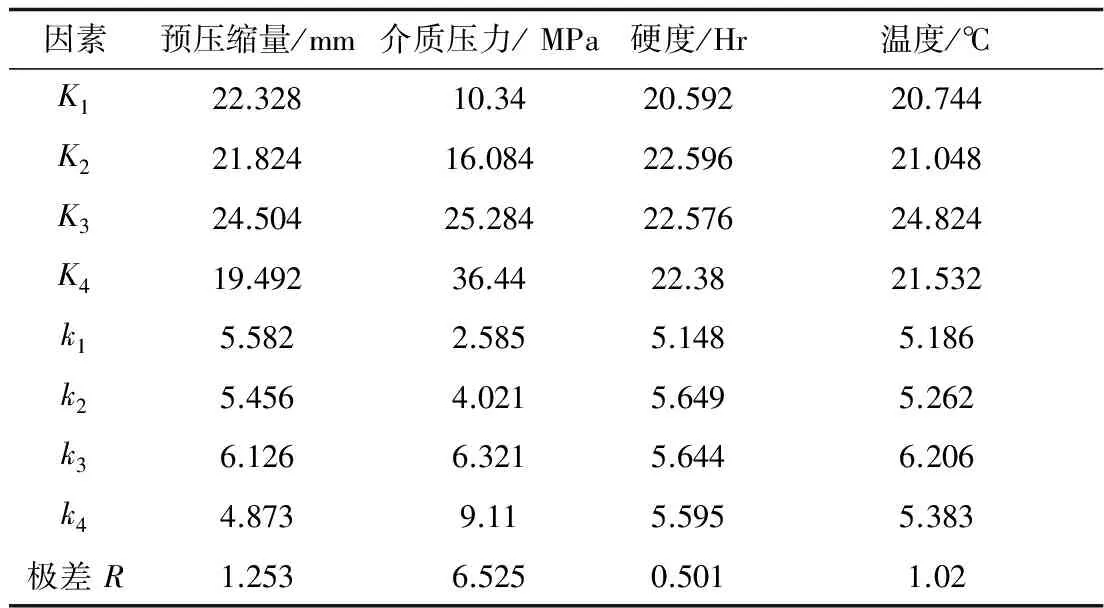
表3　最大Von Mises应力极差分析

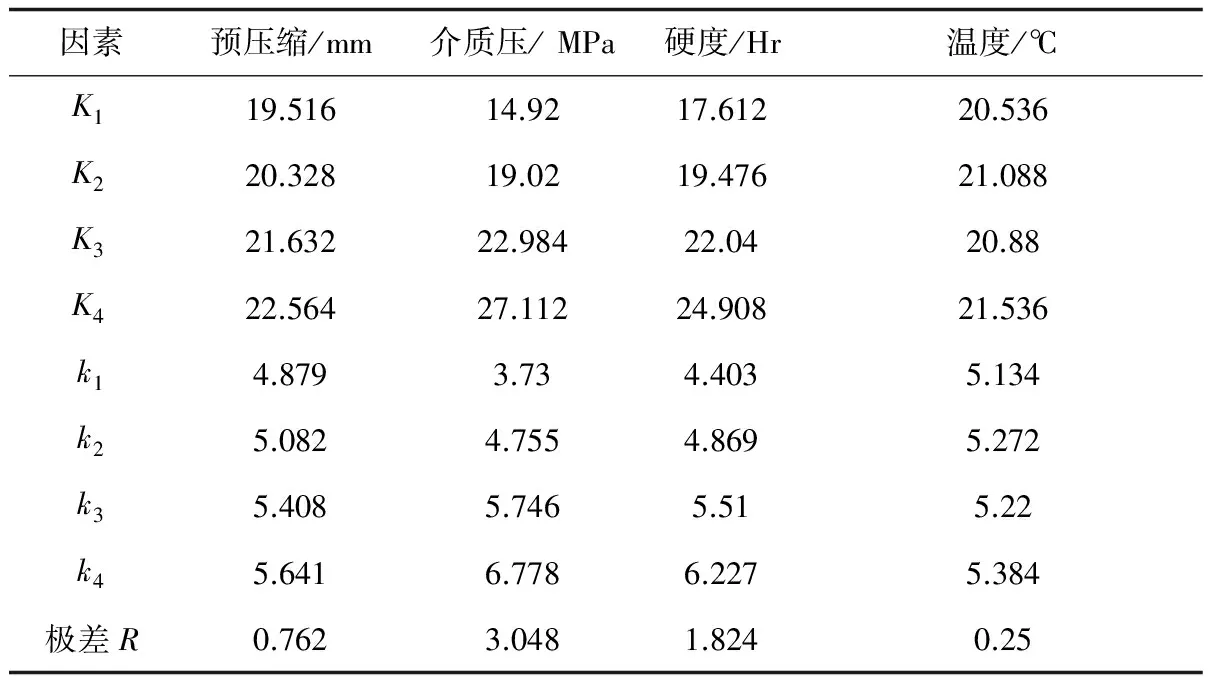
表4　最大接触应力极差分析

根据表3、表4可以得出以下结论：

1)上述4种因素对密封圈最大Von Mises应力影响的主次顺序为:介质压力>预压缩量>温度>硬度；对密封圈最大接触应力影响的主次顺序为:介质压力>硬度>预压缩量>温度。

2)当预压缩量从0.1 mm增大到0.4 mm时，密封圈的最大Von Mises应力无明显规律，主要是因为随着预压缩量增大，橡胶材料的密封圈变形不均匀引起Von Mises应力有轻微波动。密封圈介质压力过大或温度较高时，会增大密封圈的Von Mises应力，使密封圈容易发生破损，从而导致失效。硬度对密封圈的Von Mises应力的影响较小。

3)随着预压缩量、介质压力、硬度的增大，密封圈的最大接触应力也增大，温度变化对接触应力的影响效果不明显。

4　动密封特性分析

4.1　速度影响

往复运动速度是影响动密封的重要因素之一，图7、图8分别给出了动密封过程活塞杆速度v=0.1～0.5 m/s时X形密封圈的最大Von Mises应力变化曲线及主密封面最大接触应力变化曲线。

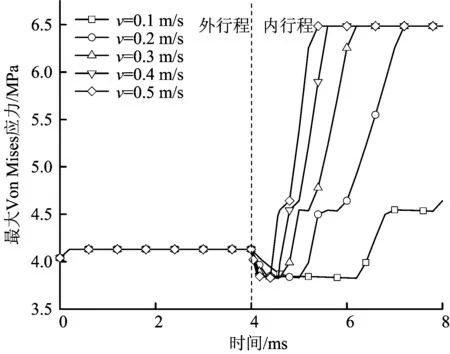
图7　不同速度下X密封圈最大Von Mises应力Fig.7　Maximum Von Mises of X-sealing ring at different speeds

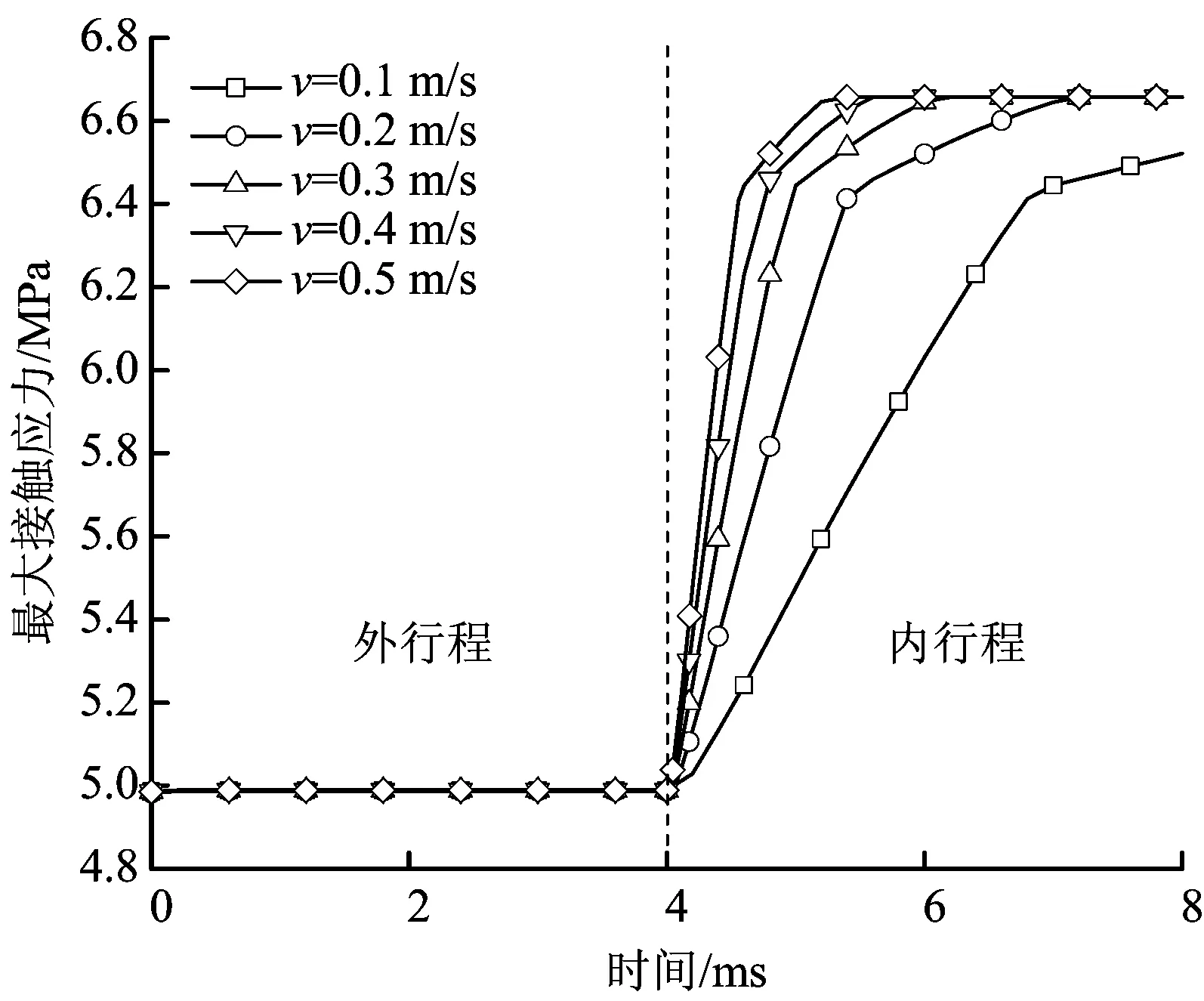
图8　不同速度下密封圈最大接触应力Fig.8　Maximum contact stress of X-sealing ring at different speeds

根据图7、图8得出以下结论：

1)在外行程过程中，不同运动速度下密封圈的最大Von Mises应力、主密封面上最大接触应力基本不变。可见，外行程过程中，速度对密封圈应力影响较小。

2)在内行程过程中，密封圈的最大Von Mises应力先减小，一段时间后逐渐增大，最后趋于稳定值；密封圈的最大接触应力先快速增大，再缓慢增大，最后趋于稳定，且达到稳定的时间随着速度的增加而变短。

3)在内行程开始时，密封圈的最大Von Mises应力、最大接触应力随速度的增大而增大；内行程结束时，在速度为0.1 m/s时具有更小的Von Mises应力。此时最大接触应力为6.52 MPa，当速度大于0.1 m/s时，密封圈最大接触应力均为6.66 MPa，说明速度较大时，密封圈更易发生破坏导致密封失效，但对接触应力影响较小。

4.2　摩擦系数影响

星形密封圈橡胶属高分子材料，分子量一般在20万以上。橡胶产品通常采用压制成型方法生产，在成型过程中极易导致橡胶材料大分子链沿某方向形成局部取向；此外，在密封圈压制成型过程中，由于模具和成型收缩率的差异[17]，密封圈的表面粗糙程度也会产生差异。因此采用橡胶制成密封圈与活塞杆、沟槽之间会具有不同的摩擦因素。图9、图10分别为动密封过程摩擦系数f=0.1～0.5时X形密封圈最大Von Mises应力变化曲线、主密封面上最大接触应力变化曲线。

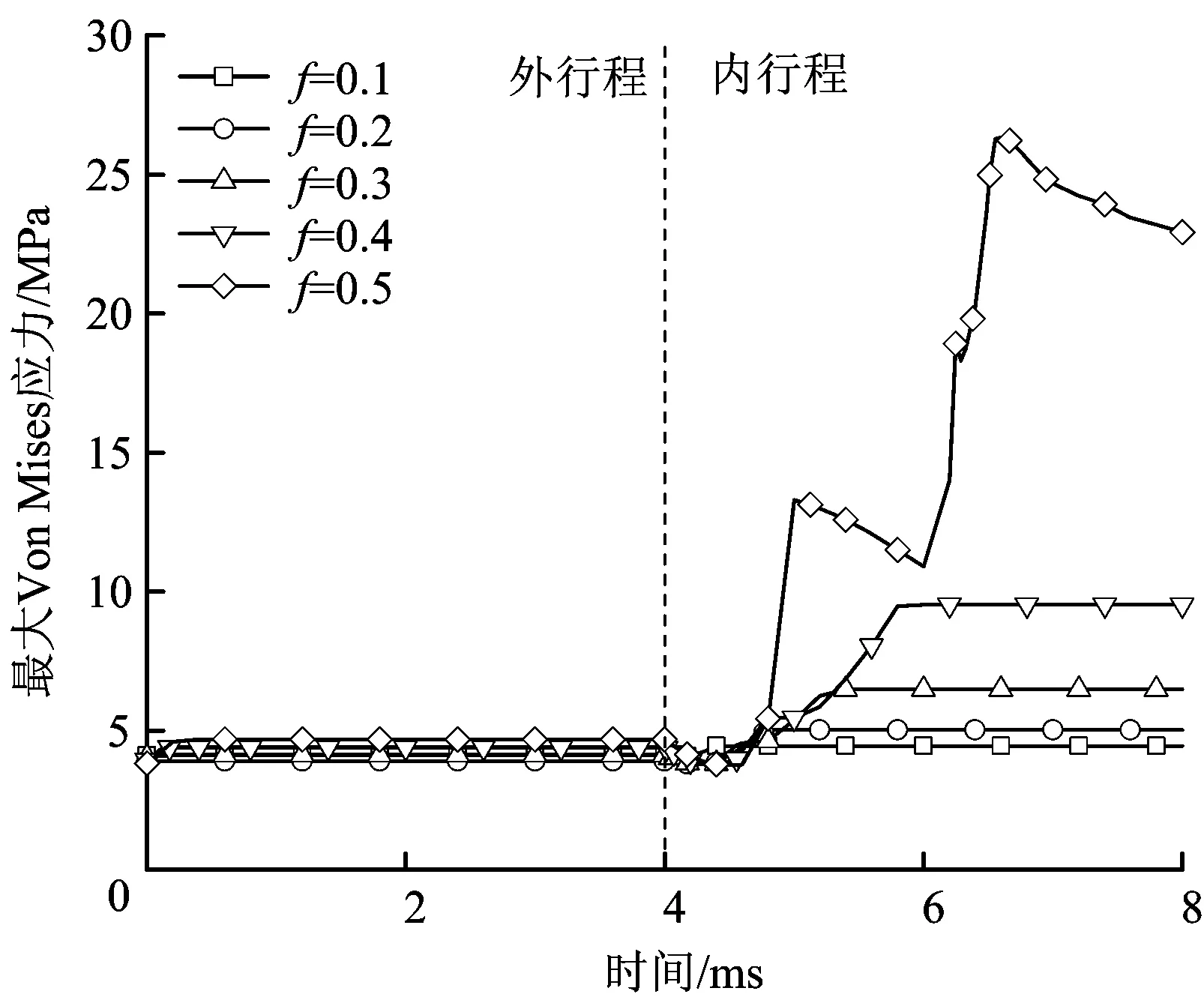
图9　不同摩擦系数下密封圈最大Von Mises应力Fig.9　Maximum Von Mises of X-sealing ring under different friction coefficient

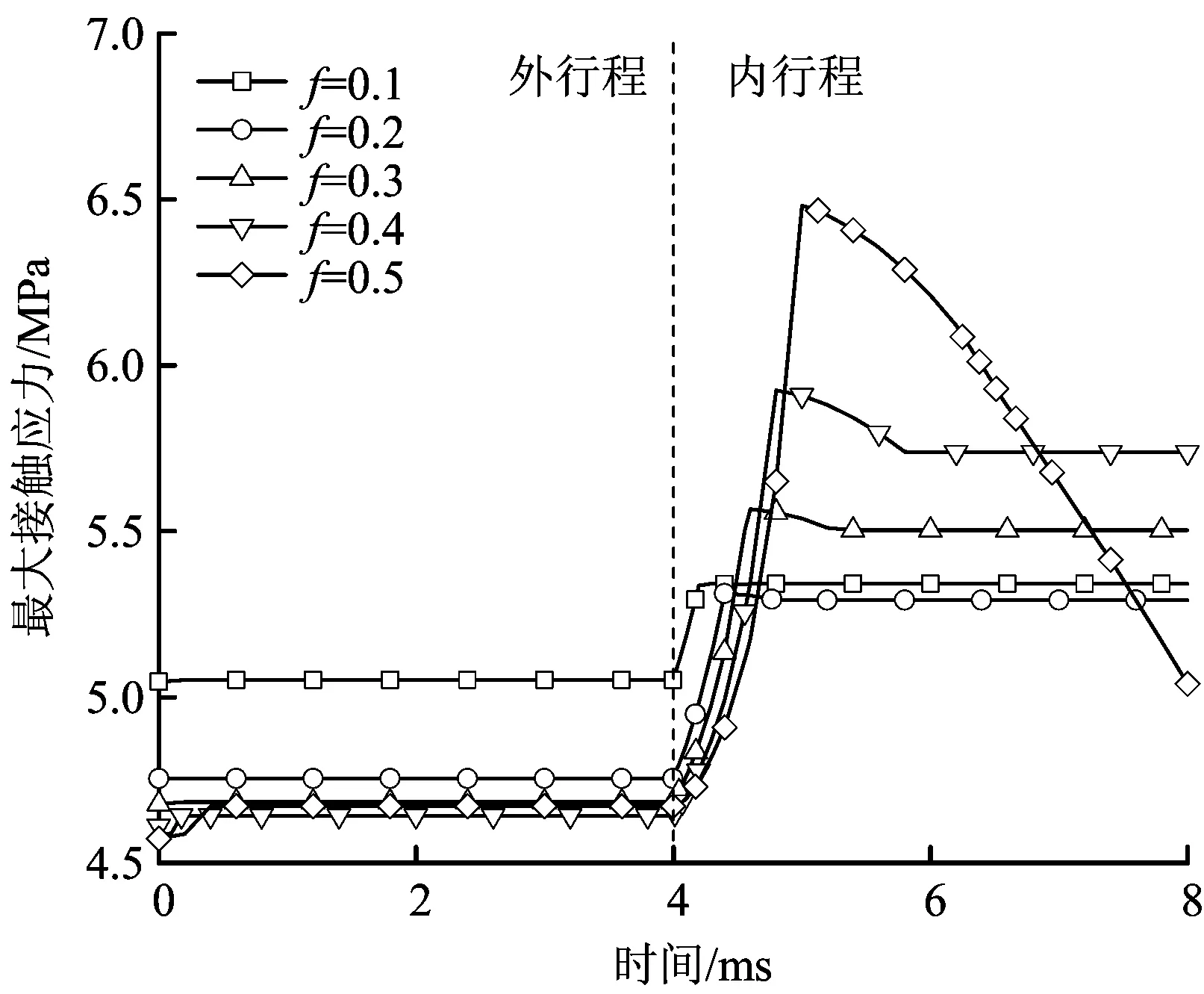
图10　不同摩擦系数下密封圈最大接触应力Fig.10　Maximum contact stress of X-sealing ring under different friction coefficient

根据图9、图10可以得出以下结论：

1)在外行程开始时，密封圈Von Mises应力有轻微增大，之后密封圈Von Mises应力快速趋于稳定，并随着摩擦系数的增大而增大。当0.1≤f≤0.4时，密封圈最大接触应力随着摩擦系数增大而减小；当摩擦系数更大时，密封圈接触应力近似相同。

2)在内行程过程中，当0.1≤f≤0.4，密封圈的最大Von Mises应力和最大接触应力逐渐增大，最后趋于稳定，且达到稳定的时间随着摩擦系数的增加而变长；当f=0.5时，密封圈的最大Von Mises应力呈“锯齿”状上升，接触应力先增大再持续减小，这是由于摩擦系数较大时，密封圈出现“爬行”现象，应力发生不均匀的波动，此时密封圈易摩擦生热导致密封失效。

5　结论

1)密封圈预压缩后在有介质压力比无介质压力作用应力分布更不均匀，活塞杆长期往复运动会导致密封圈发生疲劳破坏几率更大，但主密封面上最大接触应力大于介质压力，密封是安全的。

2)采用正交试验方法研究得到了在静密封过程中密封圈最大Von Mises应力的主次影响关系:介质压力>预压缩量>温度>硬度，主密封面上最大接触应力的主次影响关系:介质压力>硬度>预压缩量>温度。

3)在动密封外行程中，速度、摩擦系数对密封圈Von Mises影响较小，接触应力随着摩擦系数增大而减小；在内行程中，速度、摩擦系数对密封圈应力影响更加显著。

[1]邹兵，丁德武，朱胜杰，等. 石化企业设备密封点泄漏检测技术研究[J]. 中国安全生产科学技术，2011，7(12): 192-196.

ZOU Bing, DING Dewu，ZHU Shengjie, et al. Research on leakage detection for sealed points of petrochemical equipment[J].Journal of Safety Science and Technology, 2011，7(12): 192-196.

[2]文建军，丁波. 浮顶油罐密封圈油气分布数值模拟[J]. 中国安全生产科学技术，2016，12(2): 57-61.

WEN Jianjun，DING Bo. Numerical simulation on oil vapor distribution in seal ring of floating roof tank[J].Journal of Safety Science and Technology, 2016,12(2): 57-61.

[3]Zhi Chen, Tinchao Liu, Jianming Li. The effect of the O-ring on the end face deformation of mechanical seals based on numerical simulation[J]. Tribology International，2016，97: 278-287.

[4]ZhiGuo Zeng, YunXia Chen, Rui Kang. The effects of material degradation on sealing performances of O-Rings[J]. Applied Mechanics and Materials，2013，328: 1004-1008.

[5]Meng Zhang, Ai Guo Yao, Yuan ZhengLuo,et,al. The rubber O-Ring seal structure simulation research of electromagnetic measurement while drilling instrument[J]. Applied Mechanics and Materials，2012，271-272: 1717-1721.

[6]Dian Xin Li, Hong Lin Zhao, Shi Min Zhang,et,al. Finite element analysis on the influence of Back-Up ring on the sealing effect of rubber O-Ring[J]. Advanced Materials Research，2011，199-200: 1595-1599.

[7]纪军，阎宏伟.气缸O型圈动密封及温度场有限元分析[J]. 机械设计与制造，2016(2): 8-11.

JI Jun，YAN Hongwei. Finite element analysis on dynamic sealing characteristicsand temperature field of O-Ring[J].Machinery Design & Manufacture,2016(2): 8-11.

[8]Jing Wen, Xi Lu, Xiang Fu. Reliability Analysis of Y-Ring Rod Seal on the Servo Turret[J]. Applied Mechanics and Materials，2014，685: 212-216.

[9]田阔，姚山，杨通. 变压变温条件下Y形密封圈静密封特性分析[J]. 润滑与密封，2014，39(10): 82-87.

TIAN Kuo, YAO Shan, YANG Tong. Analysis on static sealing characteristics of Y-ring at variable temperature and pressure condition[J].Lubrication Engineering, 2014,39(10): 82-87

[10]刘占军，邓忠林. X形变截面橡胶密封圈应力有限元分析[J]. 润滑与密封，2007，186(2): 127-129.

LIU Zhanjun, DENG Zhonglin. Finite element analysis of stress on the rubber sealing X-ring change section[J].Lubrication Engineering, 2007,186(2): 127-129.

[11]韩传军，张瀚，张杰. 星形橡胶密封圈的密封特性分析及截面改进[J]. 机械设计与研究，2015，158(4): 90-94.

HANChuanjun, ZHANG Han, ZHANGJie. Sealing performance analysis and cross section melioration of X-Ring[J].Machine Design & Research, 2015，158(4): 90-94.

[12]Chuanjun Han, Han Zhang, Jie Zhang. Structural design and sealing performance analysis of biomimetic sealing ring[J]. Applied Bionics and Biomechanics，2015: 1-11.

[13]朱艳峰，刘锋，黄小清，等. 橡胶材料的本构模型[J]. 橡胶工业，2006，53(2): 119-125.

ZHU Yanfeng, LIU Feng, HUANG Xiaoqing，et al. Constitutive model of rubber materials[J]. China Rubber Industry, 2006, 53(2): 119-125.

[14]中国石油和化学工业协会. 硫化橡胶或热塑性橡胶拉伸应力应变性能的测定：GB/T 528-2009 [S].北京：中国标准出版社，2009.

[15]王国荣，胡刚，何霞，等. 往复密封轴用Y形密封圈密封性能分析[J]. 机械设计与研究，2014，30(6): 37-42.

WANG Guorong, HU Gang, HE Xia, et al. Chen baokang sealing performance analysis of Y-ring used on reciprocating seal shaft[J]. Machine Design & Research，2014, 30(6): 37-42.

[16]徐芝纶.弹性力学 [M]. 北京: 高等教育出版社，2006.

[17]曲宝龙，徐华静，马卫国. 基于摩擦因数的封隔器胶筒优化设计[J]. 石油机械，2015，43(2): 83-87.

QU Baolong, XU Huajing, MA Weiguo. Optimal design of packer rubber based on friction coefficient[J]. China Petroleum Machinery, 2015,43(2):83-87.