自适应滑模控制器的EPS侧风反向控制研究*
2017-04-14敖德根米根锁
敖德根, 米根锁
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
0 引言
汽车电动助力转向系统(Electric Power Steering, 简称EPS)是目前汽车主要研究的应用系统之一,具有轻巧、易调节、污染小等显著优点[1]。汽车EPS系统一般采用正向助力控制策略对驾驶员操控进行辅助,但传统正向助力控制策略易受到侧风的影响,很难符合汽车EPS系统稳定性和安全性要求。
文献[2]针对直线行驶的汽车,模拟并分析了侧风速和车速对汽车的影响;文献[3]提出了PID控制策略改善汽车EPS系统的轻便性和安全性,但PID算法鲁棒性较弱,不符合汽车EPS对实时性的要求;文献[4]提出一种H∞混合灵敏度的方法来对EPS进行控制,降低了系统稳定的时间,但系统响应的峰值较大;文献[5]采用了反向助力控制,但在1Nm的驾驶员转矩内,直接采取降低电流的措施,影响驾驶员路感;文献[6]提出了一种自抗扰技术,改善了受侧风影响的汽车纵向位移,但仿真车速较高,不符合城市汽车行驶速度。故有必要针对汽车受到侧风干扰时,EPS系统控制策略进行改进。
本文采用反向助力控制策略获取侧风干扰时的目标电流,并通过自适应滑模算法设计电机控制器对目标电流进行跟踪。当汽车受到侧风影响时,反向助力控制策略根据驾驶员输入转矩及汽车车速,电机输出相应的反向电流和反向转矩,可以适当地减小驾驶员转动方向盘的角度,防止汽车发生侧翻。在电机电流跟踪方面,自适应滑模控制器控制实际电流对目标电流的跟踪,利用滑模算法较强的鲁棒性,自适应算法参数自校正的能力,使实际电流的跟踪性能更加可靠,两者的结合有效地改善汽车EPS系统侧风干扰时的助力特性。
2 汽车EPS系统
图1为汽车EPS系统的简化模型图,转矩传感器、车速传感器及电机都与电子控制单元(Electric Control Unit,简称ECU)相连接,转矩传感器和车速传感器分别为ECU提供驾驶员转矩和汽车车速,ECU根据自身内部的助力特性曲线给电机提供目标电流及电压[7]。电机提供的助力转矩通过减速机构减速增扭后向齿轮齿条输出转矩,从而带动齿条发生位移,实现助力转向。

图1 EPS系统简化模型Fig.1 Simplified model of EPS system
1 汽车EPS系统数学模型
2.1 EPS系统动力学方程
汽车EPS系统是一个通过助力电机增加或减少助力转矩的电气传动控制系统[8]。根据牛顿定理,转向系统动力学方程为:
转向柱及转矩传感器:
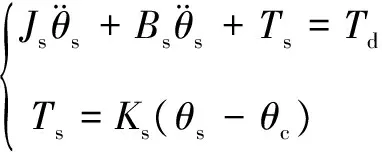
(1)
电机轴:
(2)
电机电压平衡方程:
(3)
齿条:
(4)
式中:Js为转向轴转动惯量;Bs为转向轴阻尼系数;θs为上端转向轴转角;Td为驾驶员转矩;Ts为传感器转矩;Ks为转向柱刚度;θc为下端转向轴转角;Mr为当量齿条质量;Br为当量齿条阻尼系数;Kr为齿条等效弹簧刚度;rp为小齿轮半径;xr为齿条位移;G为减速器传动比;Jm为电机转动惯量;Bm为电机的阻尼系数;Tm为电机电磁转矩;Ta为电机助力转矩;θm为电机转角;Kb为电机反电动势系数;U为电机控制电压;I为电机实际电流;R为电机电枢电阻;L为电机电感。
2.2 侧风干扰下的汽车二自由度模型
汽车受到侧风干扰时,可以在车体表面安装压力传感器进行检测,仿真时将不同的风向简化等效为垂直侧面车体的风向。为了检测在侧风干扰下汽车行驶转向的稳定性,建立侧风影响下的汽车二自由度模型[9-10],如图2所示,其动力学方程及侧风力如式(5)所示。假设侧向风方向与汽车行驶方向互相垂直,侧风力用Fy表示,一般以流入角τ的方向作用在风压中心Ac上,不与质心Mc重合[7],其大小由风速与车速合成的速度vs所决定,质心与风压中心之间的距离为力臂l,由侧风力引起的横摆力矩为Mz。工作原理为:通过将电机助力转矩和驾驶员转矩共同施加到转向输出轴,转向输出轴转角经传动比折算得到前轮转向角,并输入到侧风干扰下的汽车二自由度模型中,完成侧风模型助力。
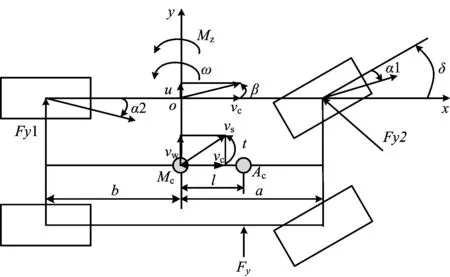
(Fy1,Fy2分别为前、后轮的侧偏力; α1,α2分别为前、后轮侧偏角)图2 侧风干扰下的汽车二自由度模型Fig.2 The two degrees of freedom vehicle model under the crosswind influence

(5)

3 反向助力控制策略设计
3.1 反向助力电流设计
在侧风干扰时,为了保证汽车安全行驶,汽车EPS并不采用常规的正向助力控制策略(随着驾驶员转矩增大,助力目标电流相应增大,且助力电机转向与方向盘转向相同的一种转向助力模式),而是采用反向助力控制策略,当汽车传感器检测到侧风压力时,执行如图3所示的反向助力控制策略框图。

图3 反向助力控制策略框图Fig.3 Block diagram of reverse power control
反向助力控制策略通过转矩传感器和车速传感器输出的信号,按照设计好的控制算法,如式(6)所示,输出相应的电机反向电流,并提供反向助力转矩以防止车轮转动过大,由于汽车在低速行驶时,不易受到侧风影响,所以将车速范围选择为40~80 km/h。为了保证驾驶员路感,反向目标助力电流在1Nm的驾驶员转矩内,保持为零,如图4所示。
Im=
(6)
式中:Im为电机的目标电流;Imax为电机的最大电流;Ts为传感器检测的驾驶员转矩;Ts0为传感器检测的驾驶员最小转矩(1 Nm);Tsmax为传感器检测的驾驶员最大转矩;K(vc)为车速感应系数,该系数随车速增加而增大。
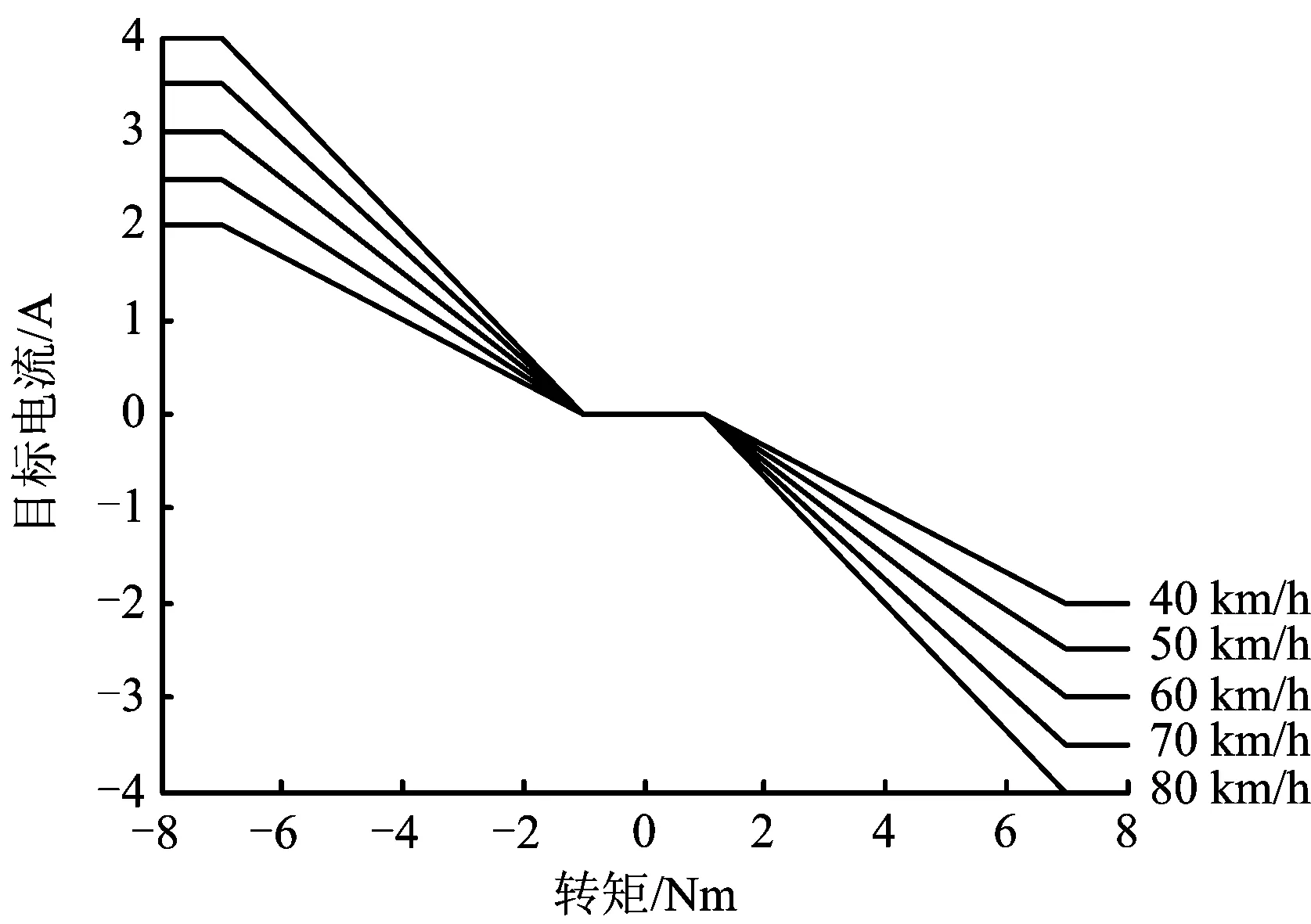
图4 反向目标助力电流Fig.4 The reverse target boost current
3.2 自适应滑模控制器设计
滑模控制是一种迫使系统状态沿期望轨迹向稳定点运动且具有强鲁棒性的控制方法。将Im设为电机目标电流,I为电机实际电流,e为跟踪误差,滑模面为:
s=e=Im-I
(7)
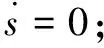
U=Ueq+Us
(8)
根据式(3)和(7),可得:
(9)
由式(9),可得等效控制项Ueq为:
(10)
选取指数趋近律为:
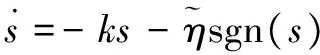
(11)

(12)
式中:λ为调节参数。
由式(11),可得切换控制项Us为:
(13)
所以结合式(10)和(13),可得控制率U为:
(14)
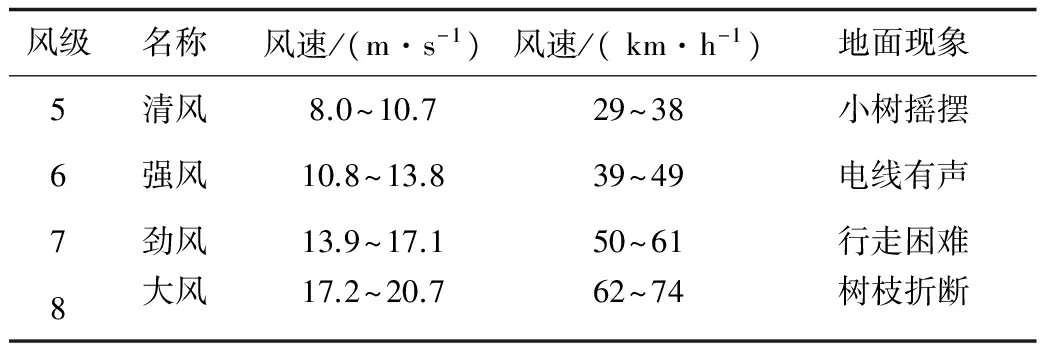
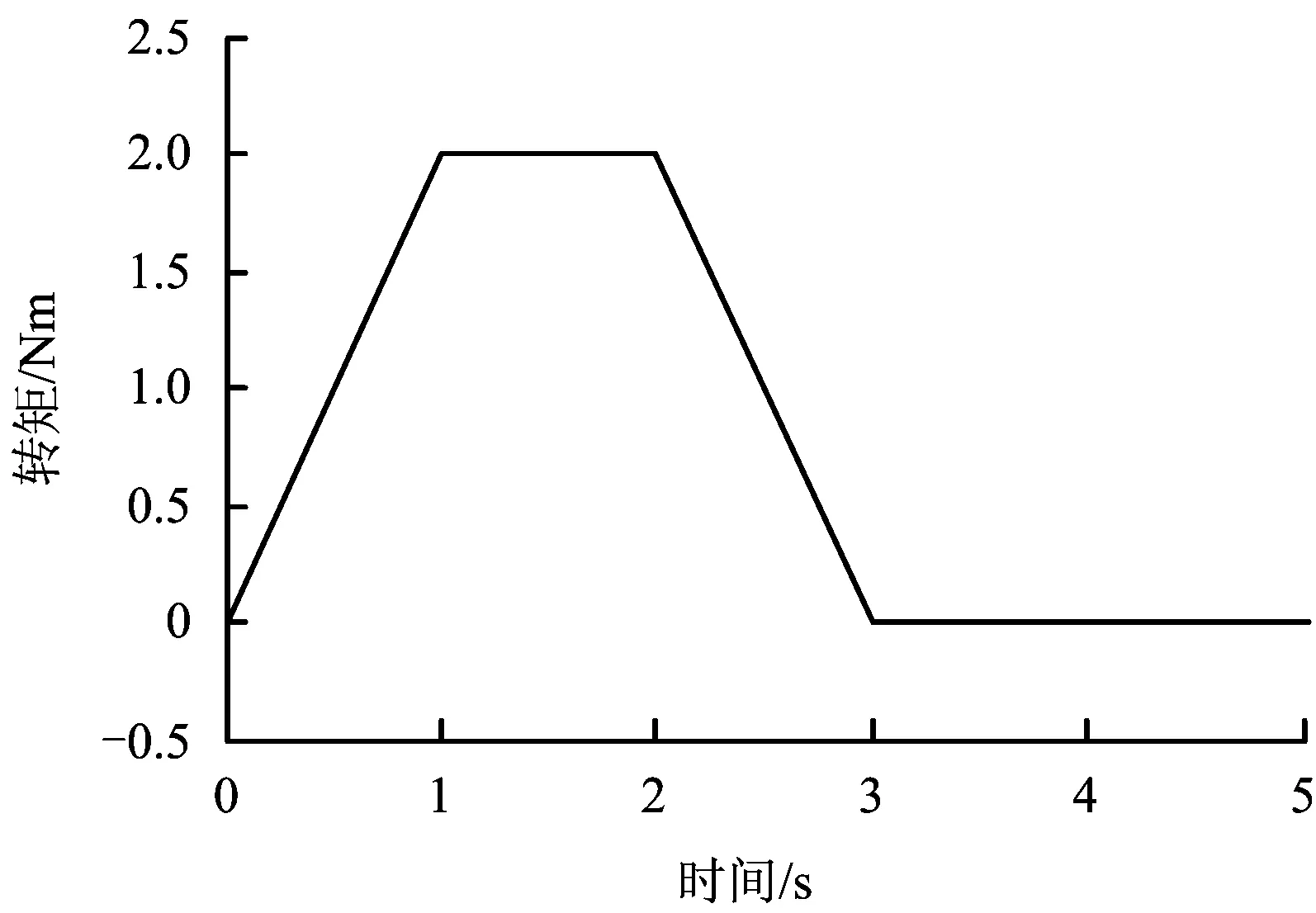
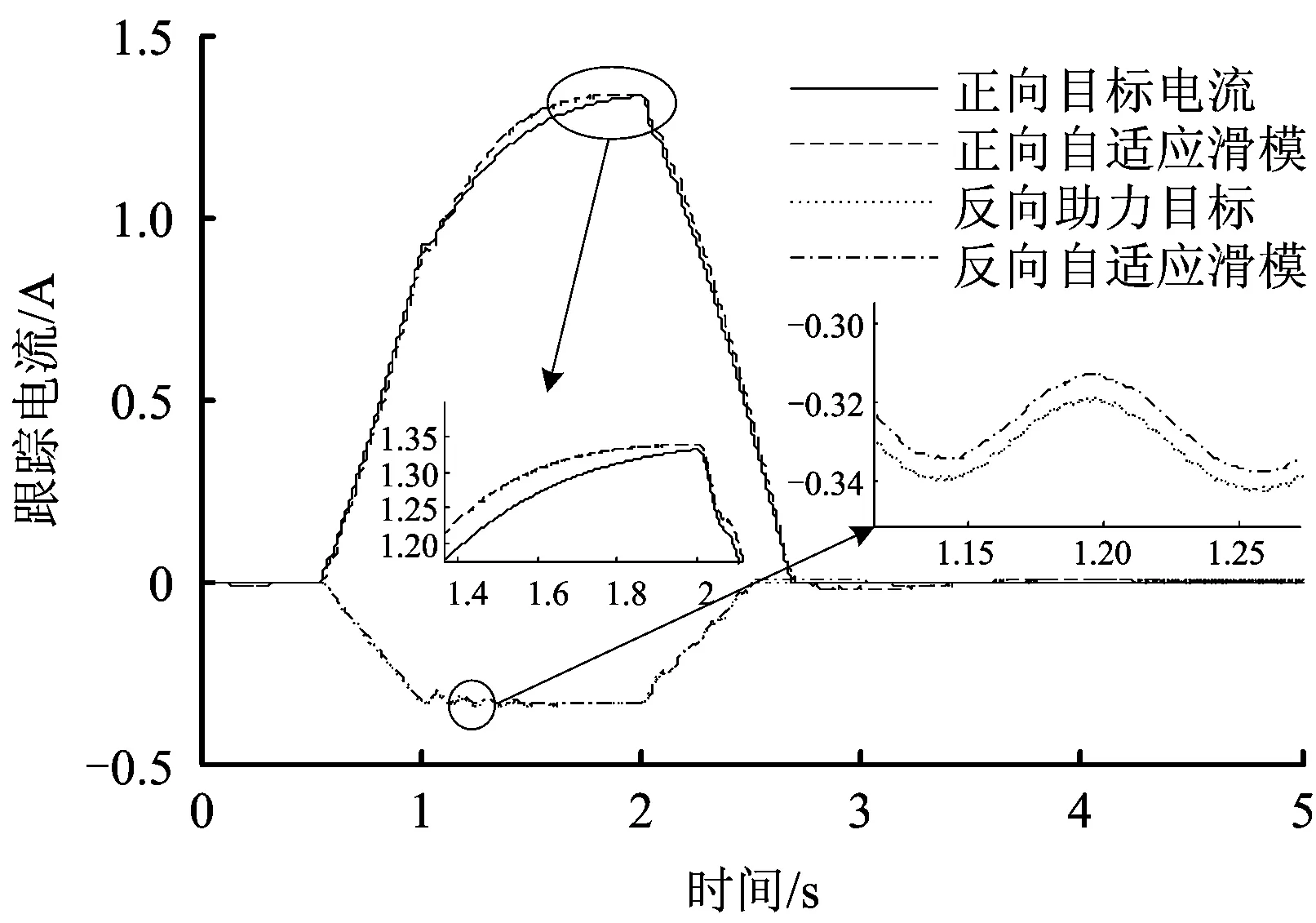
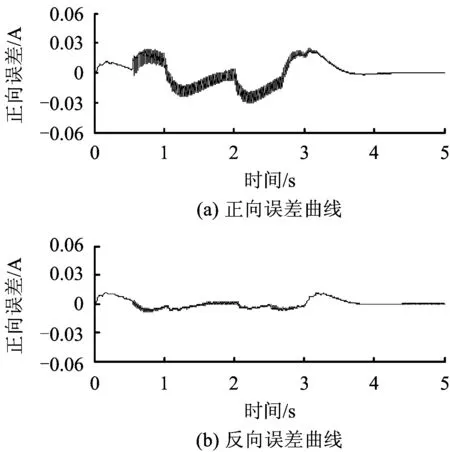
利用Lyapunov函数证明系统稳定性,设d为系统存在不确定项和外界干扰等因素,且|d| (15) 存在正常数η*=dmax,选择Lyapunov函数V为 (16) (17) 由于|d| (18) 故系统满足Lyapunov稳定性条件,汽车EPS电机系统是全局渐进稳定的。同时,为了减小切换控制引起的系统抖振,选用饱和函数替换符号函数,如式(19)所示。 (19) 式中:δ是大于零且小于1的常数。所以可得最终控制律U为: (20) 汽车在受到侧风干扰时,无论转向方向与风向相同还是相反,都需要减小方向盘的转动,以防与侧风力相顺或相斥,导致侧翻。实验在simulink平台下,并选择转向方向与风向相同的情况进行仿真。表1为风速等级表[13-14],针对正常行车时可能遇到的侧风速等级干扰,分别选择40 km/h,55 km/h的侧风速,以及40 km/h,55 km/h的车速,Cy(τ=45°)=0.9(侧风向与车身垂直,合成速度与汽车车速夹角为45°时的系数时进行仿真。 表1 风速等级 由于驾驶员转矩不可能瞬间变化到某值,所以本文选择峰值为2 Nm的梯形输入转矩来表示驾驶员转矩的实际情况,如图5所示。图6和图7分别为车速为40 km/h,侧风速为55 km/h时,在正、反向助力控制策略下,自适应滑模控制器对电机电流的跟踪曲线及电流跟踪误差曲线,可以看出,在侧风干扰下,相比正向助力,反向助力的跟踪误差及其抖振都较小,所以电流追踪效果更好。证实自适应滑模算法适应于侧风影响下的汽车EPS系统,且具有较强的鲁棒性。 图5 方向盘角度Fig.5 Steering wheel angle 图6 正、反向电流跟踪曲线 Fig.6 Positive and reverse current tracking curves 图7 正、反向电流跟踪误差曲线Fig.7 Positive and negative current tracking error curves 分别选择车速为40 km/h、侧风速为40 km/h,车速为40 km/h、侧风速为55 km/h和车速为55 km/h、侧风速为55 km/h的3种行车情况,并在正向助力、无助力及反向助力情况下进行仿真,其相应的方向盘角度,齿条位移,横摆角速度分别如图8(a)-(c)、图9(a)-(c)、图10(a)-(c)所示。 图8 车速为40 km/h,侧风速为40 km/h时的仿真结果Fig.8 Simulation result when vehicle speed and crosswind speed booth are 40 km/h 图9 车速为40 km/h,侧风速为55 km/h时的仿真结果Fig.9 Simulation result when vehicle speed is40 km/h and crosswind speed is 55 km/h 图10 车速为55 km/h,侧风速为55 km/h时的仿真结果Fig.10 Simulation result when vehicle speed is 55 km/h and crosswind speed is 55 km/h 从图8-10中可以看出,在不同的车速、侧风速下,使用正向助力会增加汽车转向时的响应指标,而使用反向助力会减小汽车转向时的响应指标。表2为图8、图9、图10的具体仿真结果数值。差值百分比为反向助力分别与正向助力和无助力在方向盘角度、齿条位移及横摆角速度方面所减小的差值百分比。从表2中可以看出,在输入转矩为3Nm的梯形转矩,车速为40 km/h,侧风速为40 km/h时,采用反向助力控制策略,相比正向助力控制策略,方向盘角度减小了64.75%,齿条位移减小了65%,横摆角速度减小了55.95%;相比无助力控制策略,方向盘角度减小了27.86%,齿条位移减小了27.59%,横摆角速度减小了21.28%。在车速为40 km/h,侧风速为55 km/h和车速为55 km/h,侧风速为55 km/h时,汽车响应的相应参数都会在反向控制策略下减小。在车速为40 km/h,侧风速为40 km/h和车速为40 km/h,侧风速为55 km/h时,由于车速不变,驾驶员输入转矩不变,从而方向盘角度和齿条位移不变,但侧风速的增加,导致汽车横摆角速度增大。在侧风速为55 km/h不变的情况下,随着车速从40 km/h增加到55 km/h,方向盘角度、齿条位移都相应减小、横摆角速度基本呈增大趋势。 表2 不同车速、侧风速下的正向助力、无助力、反向助力的汽车响应峰值 从表2中的数据结果可知,在不同的车速、风速条件下,反向助力都大大减小了汽车的响应值,这说明在侧风的环境中,反向助力更适应于汽车行驶。 1)从改善汽车受侧风干扰时的安全性角度出发,提出一种反向助力策略。通过驾驶员输入转矩和汽车车速得到反向助力目标电流,并采用自适应滑模控制器对目标电流进行跟踪。分析了不同车速和风速下对汽车系统响应的影响。 2)通过采用反向助力控制策略,减弱了侧风干扰下汽车行驶的偏移程度,使方向盘角度、齿条位移及横摆角速度有所减小,提高了汽车行驶转向的安全性和稳定性,具有实际应用价值。 [1] 任夏楠. 汽车电动助力转向系统助力特性研究及控制系统开发[D].重庆: 重庆大学, 2013. [2] 李杰, 张喆, 张英朝. 侧风对直线行驶卡车操纵稳定性的影响[J]. 吉林大学(工学版), 2009,39(S2): 255-259. LI Jie, ZHANG Zhe, ZHANG Yingchao. Effects of crosswind on handling and stability of truck driving in a straight-line[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(S2): 255-259. [3] 王其东, 秦炜华,陈无畏.基于多刚体动力学和规则协调的汽车EPS与ASS建模与控制[J]. 中国机械工程学报, 2010,21(14):1709-1713. WANG Qidong,QIN Weihua, CHEN Wuwei. Modeling and control of vehicle electric power steering and active suspension system based on multibody dynamics and rule-based coordination[J]. Journal of Mechanical Engineering, 2010,21(14):1709-1713. [4] 藏怀泉,耿佳,赵保军.基于H∞混合灵敏度控制的EPS操纵稳定性研究[J]. 北京理工大学学报, 2012,32(12): 1252-1257. ZHANG Huaiquan, GENG Jia, ZHAO Baojun. Study on handling stability of vehicle with electric power steering system based on H∞mixed sensitivity control [J]. Transactions of Beijing Institute of Technology, 2012, 32(12):1252-1257. [5] 赵景波, 周冰, 贝绍轶. 侧风干扰工况电动汽车EPS反向助力控制及试验[J]. 电机与控制学报, 2012, 16(9):103-108. ZHAO Jingbo, ZHOU Bing, BEI Shaotie. Reverse assistance control and tests of electric vehicle EPS system under anti-wind interference condition[J]. Electric Machines and Control, 2012, 16(9):103-108. [6] 白玉, 桑楠. 基于自抗扰技术的汽车侧风稳定性研究[J]. 湖南科技大学学报(自然科学版),2014,29(4): 28-33. BAI Yu, SANG Nan. Study of vehicle crosswind stability based on ADRC technology[J]. Journal of Hunan University of Science & Technology(Natural Science Edition), 2014,29(4): 28-33. [7] 文艺. 汽车电动助力转向系统的控制方法与仿真分析[D]. 广州: 华南理工大学, 2010. [8] 张辉. 基于主动四轮转向系统的高速汽车侧风稳定性控制研究[D].杭州: 浙江大学,2014. [9]张甫仁, 张金龙, 屈贤, 等. 侧风作用下汽车外流场气动特性分析[J]. 科技导报,2015, 33(15):76-81. ZHANG Furen, ZHANG Jinlong, QU Xian, et al. Numerical study on the stability of different front window angle cars in crosswind[J]. Science & Technology Review, 2015, 33(15): 76-81. [10]喻凡, 林逸. 汽车系统动力学[M]. 北京: 机械工业出版社, 2015. [11]鹿鹏程. 汽车EPS控制算法研究与实现[D]. 重庆:重庆大学, 2012. [12]GAO Qing, LIU Lu, FENG Gang, et al. Universal fuzzy integral sliding mode controllers for stochastic nonlinear systems[J]. IEEE Transactions on Cybernetics, 2014, 44(12):2658-2669. [13]张琨.侧风对公路行车安全影响的仿真分析与对策研究[D]. 西安:长安大学,2015. [14]秦小飞. 考虑风压中心位置影响下的汽车侧风稳定性及其控制研究[D]. 长沙:湖南大学, 2014.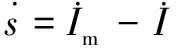
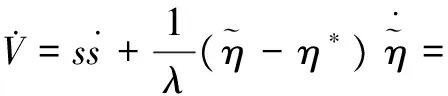
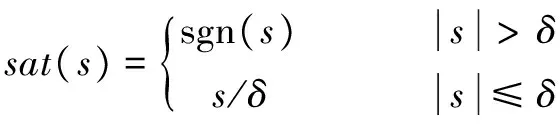
4 仿真验证及结果分析

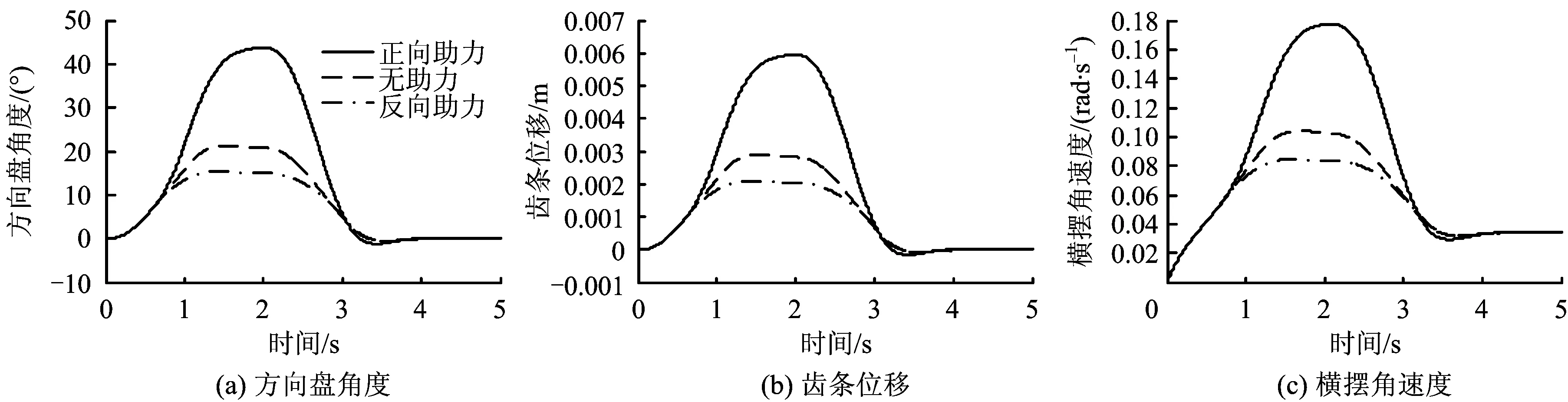
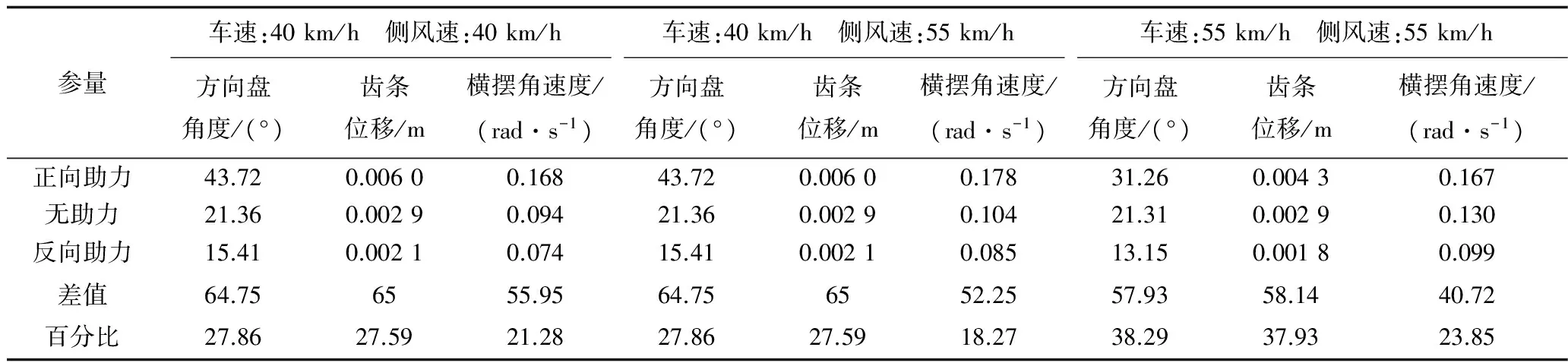
5 结论
