基于泊松过程的校车优化调度问题研究

郑秋群，王 琪，王楚菡，桂预风

(武汉理工大学 理学院，湖北 武汉 430070)

基于泊松过程的校车优化调度问题研究

郑秋群，王 琪，王楚菡，桂预风

(武汉理工大学 理学院，湖北 武汉 430070)

针对传统校车调度方案中管理不灵活的缺点，提出一种基于动态调度原理和分段齐次泊松过程的双目标优化模型。首先利用泊松分布对发车时间间隔进行非等时优化，得到发车间隔序列，再据此计算出一天内的发车时刻，最后进行泊松随机数编程模拟不同时刻的乘车人数，得到调度方案。以武汉理工大学为例进行模型检验，所得结果表明该方案易于管理、灵活方便。

校车问题；双目标规划；车辆调度；分段齐次泊松过程

0 引言

车辆调度问题[1](VRP)是组合优化领域研究的热点和难题，科学有效的调度能够让车辆正确运转，提高物流工作效率，保障企业机构运营效益。VRP问题一般可分为静态VRP问题(SVRP)和动态VRP问题(DVRP)，在实际应用过程中，由于交通拥堵情况、天气状况、安全事故等诸多因素的影响，传统SVRP问题的理论和方法已经不再适用，这使得对DVRP问题的研究更为迫切。目前，国内外对VRP问题的大部分研究还是建立在SVRP问题上，而DVRP问题更接近实际生活，解决DVRP问题的主要方法有启发式算法等，以及与其研究思想相近的方法，现已成为解决实际生活中车辆调度问题的发展热点。

随着社会经济的发展和交通的日益发达，许多高校为了满足自身需求购置校车，校车成为高校大学生在不同校区之间便捷通行的主要交通工具，高效的车辆管理和科学的安排调度不仅可以满足学生日常的交通出行，而且降低了校车运营成本，提高了校车服务质量。武汉理工大学自建校以来，由于学校合并，各校区分布较为分散，对大部分在校学生而言，课程安排和行车路线及时刻表等的变化，使得学生们一般选择乘坐校车往返于不同校区，如何对校车进行合理的调度成为长期困扰高校学生的最主要问题。本文以武汉理工大学为例，对校车进行动态VRP调度研究，从而实现校车调度问题的优化。

1 基本假设及符号说明

1.1 基本假设

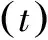
1.2 符号说明

符号说明如表1所示。

表1 符号说明

注：此表中未出现的符号说明均以出处为准

2 模型建立与求解

针对当前武汉理工大学校内校车的服务现状，结合调查结果进行分析，目前主要存在的问题是：①高峰期校车数量与规格与学生需求不均衡；②非高峰期校车发车时间安排不合理，导致等待时间过长。这两个问题严重影响到校内师生的出行质量，为了更好地解决存在的问题，本文拟从动态调度的角度出发，以学生满意度最大和校车公司的利益最大为目标，建立双目标规划模型[5]。

2.1 原始数据处理分析

由假设(2)可知，马房山校区共有5个主要校车站点，但需乘坐校车的人数较多，流动性较高的只有南湖、升升和东院3个站点。原始数据是以这3个站点为主按1min为一个基本时间单位进行搜集，分析原始数据时出现时间密度太大，数据过于离散和间断，为方便分析数据的规律性，并统计出高峰时段，将数据进行处理，把7:00-18:00统计的数据以10min为一个基本时间单位进行合并处理，合成66个时间段。由于各站点所在校区的功能属性不同，高峰期时段也有所差异，比如南湖校区主要为教学区，通常乘坐校车的人数分布会在下课时段呈峰态，升升公寓为住宿区，乘坐校车的人数分布一般在临近上课时段呈峰态。为了更直观地分析乘车人数的变化规律，用MATLAB软件画出乘车人数随时间段的变化折线图。

2.1.1 南湖校区

南湖校区乘坐校车人数统计如图1所示。

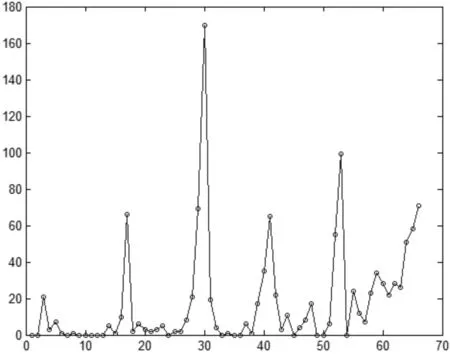
图1 南湖校区乘坐校车人数统计

由图1可看出，一天之内南湖校区共有5个乘坐校车高峰期，所在时段序号分别为17、30、41、53、66，对应的时间段为9:40-9:50、11:50-12:00、13:40-13:50、15:40-15:50、17:50-18:00，这些时段均为上下课时段，与南湖校区作为主要教学区的性质相符。

2.1.2 升升公寓

升升公寓乘坐校车人数统计折线如图2所示。

图2 升升公寓乘坐校车人数统计折线

由图2可看出，一天之内升升公寓共有3个乘坐校车高峰期，所在时段序号分别为2～4、18、41，对应的时间段为7:20-7:40、9:50-10:00、13:40-13:50。升升公寓是学生的居住区，每天需要乘坐校车的学生比例最大，高峰时段均为上课前20分钟。

2.1.3 东院校区

东院校区乘坐校车人数统计折线如图3所示。

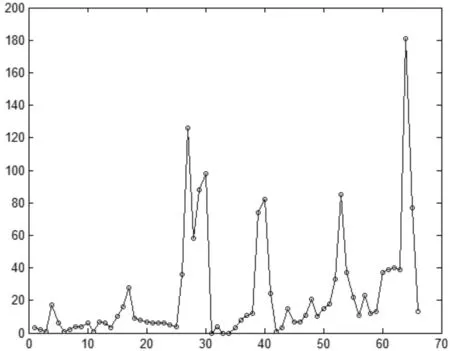
图3 东院校区乘坐校车人数统计折线

由图3可看出，一天之内东院共有4个乘坐校车高峰期，所在时段序号分别为27～30、40、53、64，对应的时间段为11:30-12:00、13:30-13:40、15:50-16:00、5:30-5:40。高峰期分布无明显规律。

2.2 车辆调度模型建立

由于校车的服务对象是学生，而学生的出行规律受一定的校内课时安排限制，故学生到达站点的强度是随时间变化的，是一个非齐次泊松过程[2]。非齐次泊松过程建模的研究难度较大，不易实施，本文拟将一天的时间离散化，分成不同的小时间段，在每个小时段内学生到达乘车站点服从齐次泊松过程。为方便统计，以10min为一个基本时间单位，从7:00-18:00共有66个基本时间单位，T=66。结合现实中校车调度问题和泊松随机过程理论[2]，有：

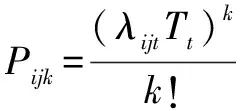
在一个发车时间间隔△Tijt内，有k个学生到达i站点的概率为：

从学生满意度最大化角度考虑，学生的满意度主要受到等车时间的影响，等待时间越长，满意度越低；从校车公司的利益角度分析，满载率越高，即空车率越低，利益就越大[4]。因此最终的解决方法是设置一个合理的校车调度方案，求出使得这两个目标值达到最大的最优解。

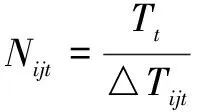
对S(t) 求期望，得到第t个时段从站点i到站点j学生等待时间总和的期望值为：

(1)

同理得到第t个时间段从站点i到站点j的空座率为：

(2)

综合式(1)和式(2)得到以学生满意度和以校车公司利益为目标的目标函数如下：

2.3 模型求解

上文得到一个使学生满意度和校车公司利益最优的非线性双目标规划模型，由于求解此模型比较复杂，故考虑转换思路，即通过选择合理的发车时间间隔△Tij，使得在△Tij时间段内，乘坐校车的人数在[Q,αQ]之间的概率最大。其中，假设超载人数不能超过校车容量的一半，即α∈[1,1.5]。因此可将双目标规划模型转化为单目标规划如下：

(3)

以南湖校区为例，取α=1.5，假设高峰时段均发容量为60的车，非高峰时段均发容量为30的校车，得到南湖校区一天之内的发车时间点如表2所示。

表2 南湖校区发车间隔

2.4 模型检验

为检验所建模型的有效程度，以南湖校区为例，进行泊松随机数编程模拟不同时刻的乘车人数，对其一天的发车情况进行模拟，计算机模拟所需参数值以表2列出的为准。

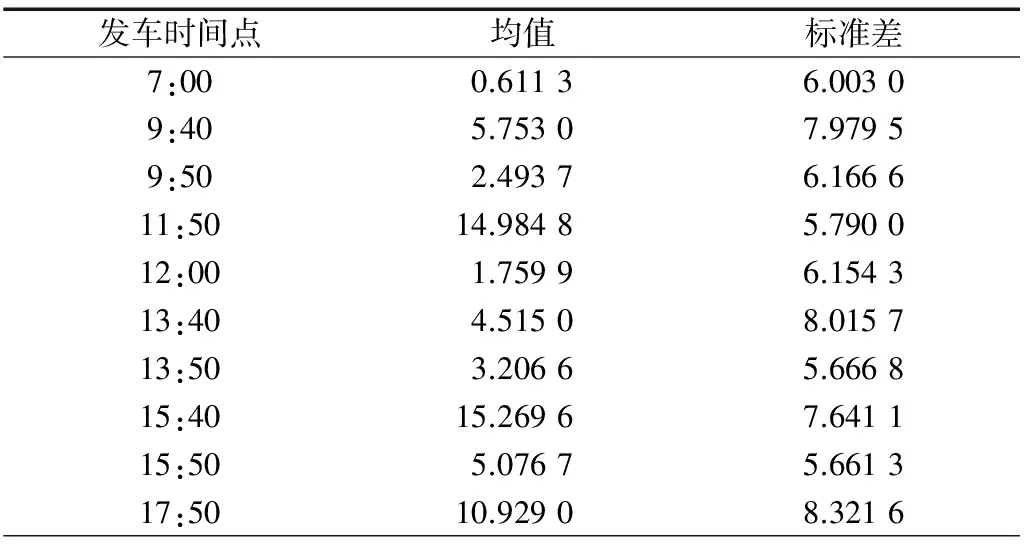
表3 南湖校区发车情况模拟结果

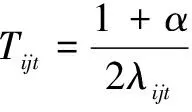
3 结语

如何安排和设置发车时间间隔从而使学生和校车公司的满意度最大是车辆调度的目的。本文以武汉理工大学马房山校区为例，利用搜集的原始数据，以学生的满意度和校车公司的利益最优为双目标，依据泊松分布建立相应的校车优化调度模型，得到不同时间段的发车时间间隔。最后以南湖校区为例，利用泊松随机数编程模拟不同时刻的乘车人数，模拟出1 000天的发车情况，得到剩余等车人数的均值和标准差较小，模型比较合理，能够为武汉理工大学校车调度问题提供较好的解决方案。但本文得到的计算结果是基于假设得到的，简化了实际情况，比如在人流量极为庞大时，会出现校车的服务强度小于乘客到达速率的情况，乘客的等待时间就可能会大于一个发车间隔。如何把多种实际情况考虑到模型中并计算出结果将是下一步研究的重点。

[1] 刘云霞.动态车辆调度问题分析及算法设计[D].成都：西南交通大学，2004.

[2] 陈家清,赵华玲.应用随机过程[M].武汉：武汉理工大学出版社，2014.

[3] 罗良浩,陈亮.论天津市公交校车的现状及发展前景——车辆调度和网络优化[C].中国城市交通规划2009年年会暨第23次学术研讨会论文集,2009.

[4] 赵莎莎,熊伟,余万玉,等.高校校车最优调度与配置方案——以三峡大学为例[J].科技创新与应用,2015(32):7-9.

[5] 杨梅,赵克全.基于多目标规划模型的校车最优配置与调度方案[J].西南师范大学学报：自然科学版,2014(6):50-54.

(责任编辑：孙 娟)

武汉理工大学自主创新研究基金项目(166814007)

桂预风(1963-)，男，湖北黄梅人，博士，武汉理工大学理学院教授、硕士生导师，研究方向为统计建模。

10.11907/rjdk.171065

TP319

A

1672-7800(2017)003-0128-03