Matlab编程避免使用循环语句的方法
2017-04-13周德亮邢泽宁
李 冰,周德亮,邢泽宁
(辽宁师范大学 数学学院,辽宁 大连 116000)
Matlab编程避免使用循环语句的方法
李 冰,周德亮,邢泽宁
(辽宁师范大学 数学学院,辽宁 大连 116000)
充分利用Matlab丰富的矩阵运算功能,解决距离矩阵的生成、一次性生成N项和函数在多个节点的函数值、一次性绘制多个节点及多个几何图形的问题。同时进行不同编程方式在生成有限覆盖子域图形时所用时间的对比实验,结果表明,这种矩阵化编程方法语言简洁,且程序运行速度更快。
Matlab;矩阵化编程;矩阵生成;和函数计算;多图形绘制
0 引言
一般编程语言在处理大量数据生成的数组或者矩阵问题时,多数采用循环语句实现[1]。Matlab语言不仅可以使用循环编程,同时可以利用其特殊的函数运算[2-3],将矩阵作为变量的基本单位,充分利用矩阵化运算代替循环编程[4]。本文利用Matlab矩阵运算,结合研究中遇到的几个问题,通过对距离矩阵的生成[5]、N项和函数的计算及有限覆盖子域的绘制几个实例,介绍了几种解决这些实例的矩阵化编程方法。
1 距离矩阵生成
考虑如下形式矩阵的生成方法,在径向基插值和配点法中经常用到距离矩阵,即:
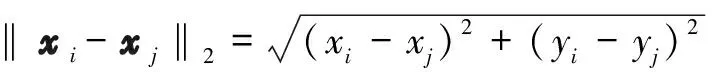
传统方法一般使用双循环语句,而使用Matlab编写程序可以避免循环。为了生成该矩阵,需要先构造如下形式的矩阵:

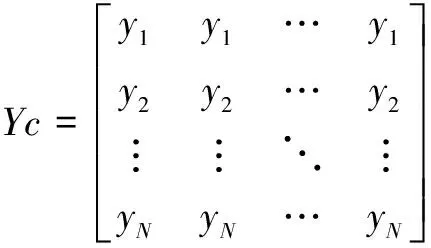
由于Ndgrid函数的功能是生成函数和插值所需的X和Y分量的网格数据,可利用Ndgrid函数生成矩阵Xc、Xr、Yc、Yr,如下:
x=0:0.1:1;y=0:0.1:1; [X,Y]=meshgrid(x,y);P=[X(:),Y(:)];
[Xc,Xr]=ndgrid(P(:,1));[Yc,Yr]=ndgrid(P(:,2));
A=sqrt((Xc-Xr).^2+(Yc-Yr).^2);
在区域[0,1]*[0,1]内布置节点x、y,其中X代表xi构成的向量,Y代表yi构成的向量,P代表将矩阵X和Y的元素按列排序。Ndgrid函数生成Xc、Xr、Yc、Yr矩阵后,利用Matlab对矩阵的“点”运算得到A,即Matlab将矩阵作为变量,对矩阵的每一个元素进行直接运算。
本文以生成2-范数距离矩阵为例。同理,当矩阵A中元素为任意范数形式时,可以求得任意N维空间的距离矩阵。
2 一类和函数计算

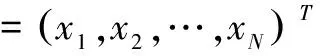
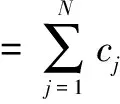
因此可编程如下,其中“%”部分为程序注释。
N=50;rbf=inline('sqrt(1+(e*r).^2)','r','e') ;e= .006; %定义节点数及径向基函数,e为参数。
x=linspace(0,5,N);%布置节点为列向量。
kxi=linspace(0,10,N);rand('state',4);c=rand(N,1); % 布置已知空间节点及系数c。
Pf=rbf(abs(repmat(x',1,N)-repmat(kxi,size(x'),1)),e)*c;

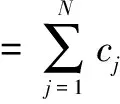
程序为:
N=50;rbf=inline('sqrt(1+(e*r).^2)','r','e');e=0.006;
kxi=linspace(0,10,N);rand('state',4);c=rand(N,1);
A=ones(size(x));E=eye(n); % 生成全1矩阵及单位矩阵。
m=10;n=20;x=fix(10*rand(m,n)); % 在[0,10]内生成m行n列的矩阵。
Pf=rbf(abs(repmat(x,1,N)-kron(kxi,A)),e)*kron(c,E);
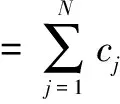
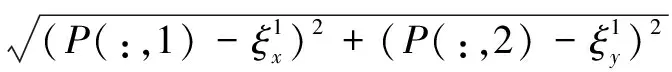
其中,P(:,1)为Matlab编程语言,代表矩阵P的第一列,P(:,2)代表矩阵P的第二列。
其程序可编写为:
rbf=inline('sqrt(1+(e*r).^2)','r','e') ;e= .006;
N=25;rand('state',4);P=fix(10*rand(N,2)); % 生成N行2列的矩阵P。
kxi=linspace(0,10,N);c=rand(N,1);
Pf=rbf(sqrt((kron(ones(1,N),P(:,1))-kron(kxi,ones(size(P(:,1))))).^2+...(kron(ones(1,N),P(:,2))-kron(kxi,ones(size(P(:,2))))).^2),ep)*c;

即Matlab矩阵化编写程序如下:
N=50;rbf=inline('sqrt(1+(e*r).^2)','r','e') ;e= .006;
kxi=linspace(0,10,N);rand('state',4);c=rand(N,1);
x=0:2:10;y=5:5:20; [X,Y]=meshgrid(x,y) % 生成网格节点X,Y。
Pf=rbf(sqrt((repmat(X,1,N)-kron(kxi,ones(size(X)))).^2 ...+(repmat(Y,1,N)-kron(kxi,ones(size(Y)))).^2),ep) *kron(c,eye(length(x)))
Matlab函数在处理数据时采用矩阵运算,避免了对节点个数及空间维数的双重循环编程。在径向基函数配点法的实际应用中,这种网格节点编程方式经常用于散乱数据节点的布置。
3 网格、节点及子域边界绘制
考虑如何不使用循环编程,一次性绘出如图1和图2所示的多个节点及多条直线图形。
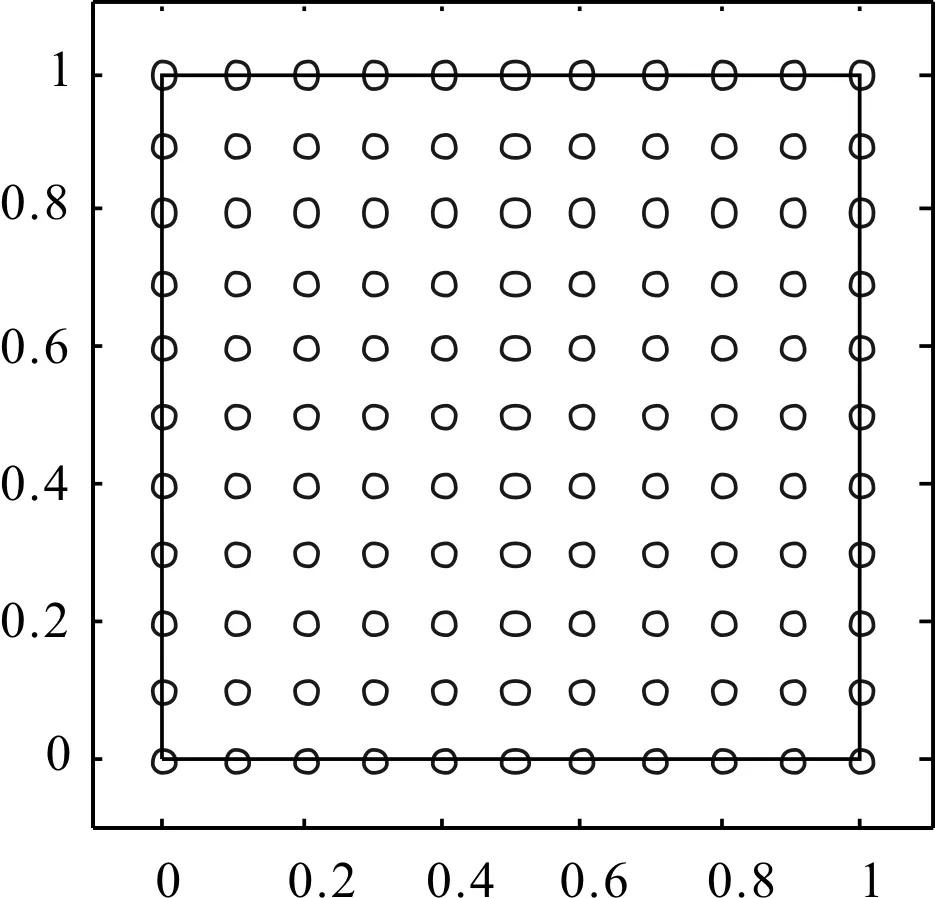
图1 同时绘制多个节点
图2 一次性绘制多条直线
利用Matlab编程可以实现一次性绘制多个几何图形。
x=0:0.1:1; y=0:0.1:1; [X,Y]=meshgrid(x,y);
figure(1); plot(X,Y,'bo','MarkerSize',5); figure(2); plot(X,Y,'k',Y,X,'k');
径向基函数单位分解配点法的应用中,在布置多个节点后,需要选择有限覆盖子域。一般地,选择矩形、圆、椭圆或球作为覆盖图形。
本文以椭圆覆盖图形为例,在[0,1]*[0,1]区域内一次性绘制多个以c为中心点的椭圆(见图3)。
hold on
c=0.1:0.2:0.9; n=length(c); % n为横坐标布置的中心点长度
[Xc,Yc]=meshgrid(c); XYc=[Xc(:),Yc(:)];
m=linspace(0,2*pi,n.^2)'; a=0.185; b=0.14; % m为极坐标下布置角度,a,b为参数
CX=kron(ones(1,n^2),Xc(:))'+kron(ones(1,n^2),a*cos(m)); %生成每个子域的边界横坐标
CY=kron(ones(1,n^2),Yc(:))'+kron(ones(1,n^2),b*sin(m)); %生成每个子域的边界纵坐标
plot(CX,CY,'r',Xc,Yc,'k.');
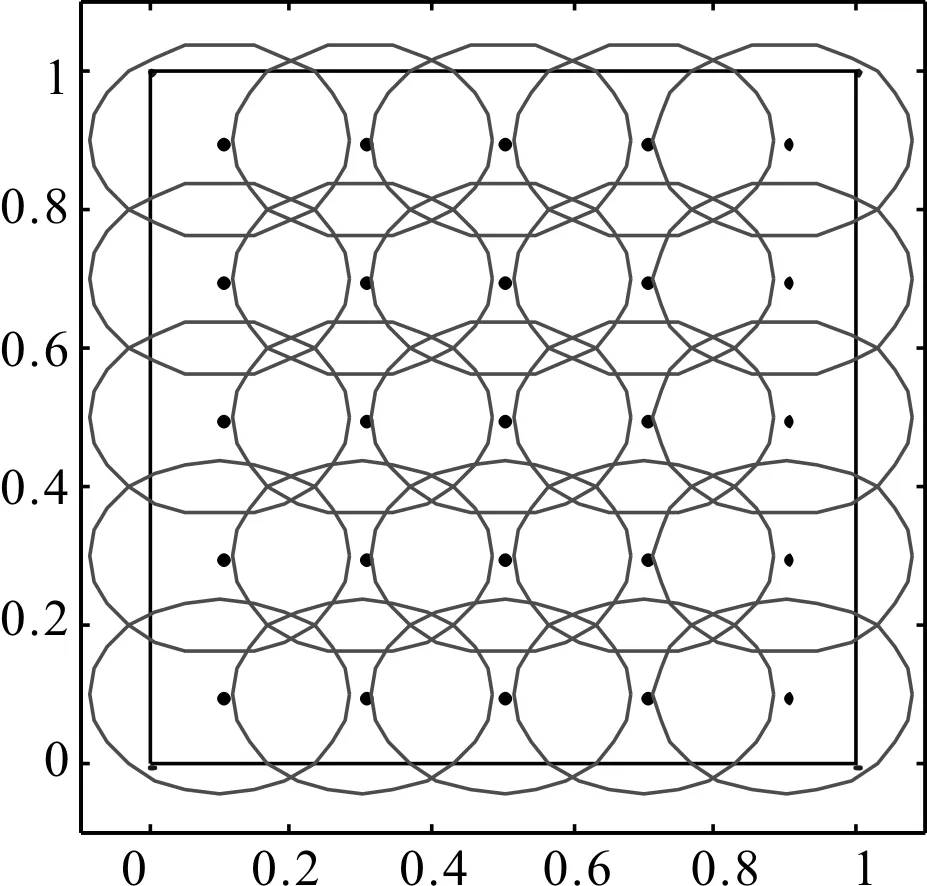
图3 椭圆形覆盖域
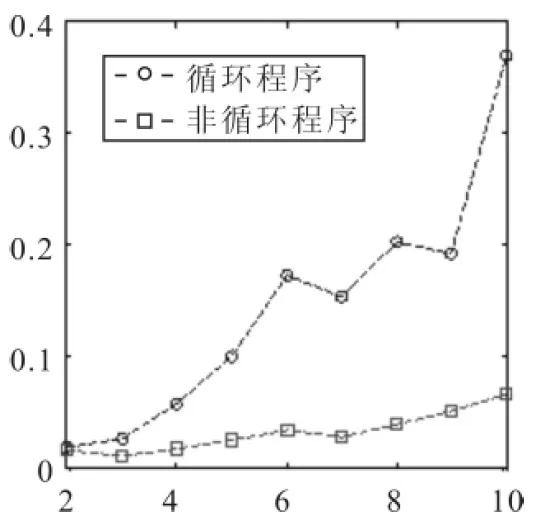
图4 时间对比
在绘制椭圆形覆盖域时,使用Matlab中计时函数tic、toc对程序运行的时间进行检测,同时利用如下循环程序进行对比实验。时间对比如图4所示。
for i=1:Nc
CX=XY(i,1)+a*cos(m); CY=XY(i,2)+b*sin(m);
plot(CX,CY,'r');
end
实验对比表明,当中心点个数c增大,椭圆域个数增加时,Matlab将一组数据进行矩阵向量化编程,同时绘制多个几何图形,提高了程序的运行效率。
4 结语
本文用3个科研中遇到的应用实例问题,利用Matlab在矩阵数据处理上的优势,实现了以矩阵化编程代替循环程序的过程,体现了Matlab矩阵化编程方法在提高程序运行效率上的优势。
[1] 顾丽红,李传秀,吴少刚.矩阵乘法C语言程序设计案例探究[J].计算机教育,2016(1):149-152.
[2] 杨亚辉.用Matlab深入学习和理解矩阵知识[J].现代电子技术,2007(6):175-177.
[3] 鄢喜爱,杨金民,田华.Matlab在数据处理和绘图中的应用[J].科学技术与工程,2006(6):3631-3633.
[4] KANSA E J.Multiquadrics—a scattered data approximation scheme with applications to computational fluid dynamics II. Solutions to parabolic,hyperbolic and elliptic partial differential equations[J].Comput Math Appl,1990,19(8/9):147-161.
[5] 张志涌,杨祖樱.MATLAB教程R2012a[M].北京:北京航空航天大学出版社,2010.
(责任编辑:孙 娟)
李冰(1990-),女,辽宁昌图人,辽宁师范大学数学学院硕士研究生,研究方向为科学计算可视化;周德亮(1960-),男,辽宁沈阳人,博士,辽宁师范大学数学学院副教授、硕士生导师,研究方向为微分方程数值解法及应用;邢泽宁(1992-),女,辽宁昌图人,辽宁师范大学数学学院硕士研究生,研究方向为科学计算可视化。
10.11907/rjdk.162869
TP301
A
1672-7800(2017)003-0015-03
