考虑直流干扰条件下的变电站二次直流系统故障检测新算法

朱德亮 苏建明

（安徽省电力公司铜陵供电公司，安徽 铜陵 244000）

考虑直流干扰条件下的变电站二次直流系统故障检测新算法

朱德亮 苏建明

（安徽省电力公司铜陵供电公司，安徽 铜陵 244000）

线性正弦跟踪器（linear sinusoidal tractor，LST）对于特定频率信号具有良好的幅频和相频特性，注入信号法的直流接地故障检测易受支路分布电容的影响。本文提出了一种基于离散LST算法的改进型变电站二次直流接地故障检测算法，分析了检测系统等效电路数学模型，将LST算法经过旋转变换，直接分离出LST算法检测到的交流电流信号中电阻电流以及对地等效电容电流值，通过对待测信号一阶微分滤除直流分量，调节跟踪器参数，分离出特定频率待测交流信号，根据接地电阻以及等效电容计算公式得到各支路接地电阻及对地电容。仿真结果表明，该算法能够克服分布电容对检测结果的影响，准确检测出接地故障。

线性正弦跟踪器；直流接地；一阶微分；旋转变换

变电站二次直流系统为保护、测控及一次设备提供装置电源及操作电流，直流故障作为危急缺陷严重影响电网安全稳定运行。直流故障表现为正负直流电压不平衡，直流正接地容易造成保护装置误动，负接地会造成保护装置拒动，继而引起电网安全事故。

对于变电站二次直流系统接地故障检测主要分为电桥检测法[1-3]及信号注入法[4-5]。电桥检测法主要分为平衡电桥检测法以及不平衡电桥检测法，不平衡电桥检测法能够避免直流混接时电桥的引入引起的直流母线正负电压偏差问题，对检测支路接地故障具有一定的灵敏度。注入信号法易受到检测支路分布电容的影响，通过引入先进的信号处理方法[6-10]能够消除分布电容影响，为典型代表的基于小波分析的直流接地故障检测算法能够大幅度提高检测精度。文献[11]分析了基于复值小波变换和Morlet小波变换的检测方法，通过仿真分析证明了两种小波变换算法均能够有效消除支路分布电容对检测结果的影响，有效提高了检测精度。文献[4]利用分形维数和凹凸度参数惟一确定的二维平面上点的位置，来检测不同情况的接地故障。文献[12]提出了一种正弦跟踪器算法，通过调节滤波器参数实现任意频点任意带宽的线性滤波器，具有稳定的幅频和相频特性。文献[13]将该算法通过四阶龙格-库塔微分方程式解法将算法引入嵌入式系统，为实用化提供了理论基础。文献[14]利用正弦跟踪算法实现变电站二次直流系统接地检测，证明算法具有良好的检测精度，能够同时检测出支路接地电阻和对地电容值，但未考虑在获取的低频信号中有直流信号干扰，会影响测量精度。

本文提出了一种基于离散化LST算法的改进型直流故障检测实用化特点，通过分析LST算法易受直流信号干扰，改进检测步骤，对待测信号进行一阶微分，将LST算法进行旋转变换直接分离出电阻电流及等效电容电流有效值，通过接地电阻及电容计算公式得出结果，仿真结果表明该算法具有良好的检测精度，能够全面反映变电站二次直流系统故障，实用化前景较好。

1 直流检测系统等效电路

变电站二次直流系统通常由整流模块整流得到正负直流110V电压，由直流屏分成直流Ⅰ、Ⅱ段母线，各间隔直流接至母线排，检测等效电路如图1所示。

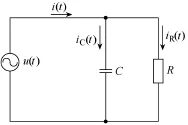
图1 变电站直流系统检测等效电路

令u(t)=Usin(ωt)为注入交流电压，根据图1所示的等效电路图得

式中，iC(t)、iR(t)分别为支路对地电容电流和接地电阻电流，将i(t)=Isin(ωt+ϕ)及u(t)代入式（1），对上式进行变换得

式中，U为注入交流电压幅值有效值，ω为交流信号角频率，I为支路交流电流有效值。由式（2）得出接地电阻及对地电容计算式为

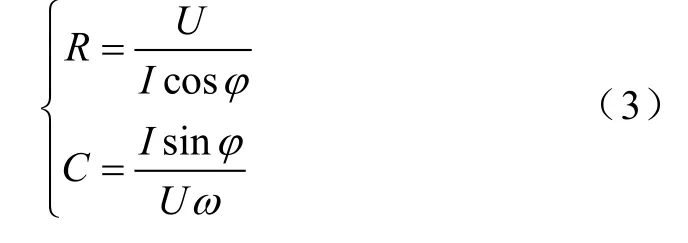
2 考虑直流干扰检测算法原理

2.1 算法检测原理

正弦跟踪器算法是基于最小二乘法对正弦信号的估计，通过旋转变换将幅值和相位解耦，获得对已知频率信号的无幅值偏差、无相位延迟的无限冲激响应滤波器，算法的实现如式（4）所示：

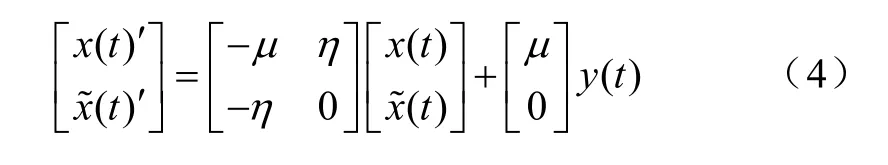
式中，y(t)为检测信号，η=ω为待测信号的角频率，x(t)为i(t)的估计信号，(t)为滞后x(t)角度90°信号，μ为滤波器参数，x(t)′、(t)′分别为x(t)、(t)的一阶微分信号。改变频率参数η可使滤波器延频率轴方向移动，改变滤波器参数μ可决定滤波器收敛速度。

将式（5）代入式（1）可得

如上式所示，通过正弦跟踪器检测出u(t)、i(t)的估计信号，通过旋转变换得出z1及z2，根据已知数据可检测出对地电容值和接地电阻值。

考虑到经典四阶龙格-库塔方法具备四阶精度，只具有四级计算量，属于单步方法，不需要迭代计算，应用最为广泛，故以此为基础来讨论所提算法的计算机实现。针对式（4）的方程，运用四阶龙格-库塔方法将上述算法进行微分求解。

在式（7）中，第m次采样得到数值y(m)，计算得到中间变量G1、G2；在经过采样周期的一半即T/2时刻得到采样数值，根据式（8）得到中间变量H1、H2，以此类推分别可以求出中间变量J1、J2，K1、K2；将上述得到的中间变量带入式（11）就得到了计算x[m]和[m]的递推公式，在通过式（5）的旋转变换以及式（6）的计算公式，可准确求得接地电阻以及对地电容值大小。

2.2 直流信号干扰研究

上述正弦跟踪器算法针对特定频率的交流信号的检测，但在检测直流系统中需考虑到直流信号与所注入交流信号的叠加，造成交流信号幅值偏移，算法精度下降。如图2（a）所示。

图2 考虑直流信号干扰检测图

在无直流干扰条件下，算法检测精度较好，但在加入幅值为1.5的直流信号条件下，算法检测结果产生畸变，故在提取信号源检测时，需要滤除直流分量。

定义检测信号源如式（12）所示：

对式（12）进行两边对时间t进行求导，得到式（13）：

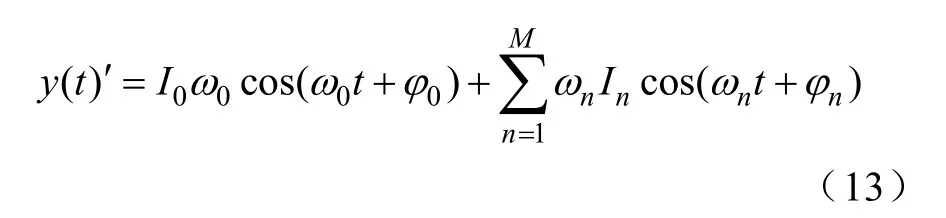
式（13）中已将直流信号滤除，而其余包括待测信号交流量由正弦量变为余弦量，幅值增大为角频率的倍数。

3 仿真应用分析

本文采用Matlab工具对上述算法进行仿真分析，二次直流系统如图3所示，信号发生器电源为u(t)=10sin(30πt)，直流母线电压为正负110V，负载1-4分别为40kΩ、20kΩ、15kΩ、30kΩ。滤波器参数分别为μ=20π，η=30π。

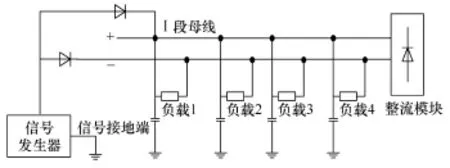
图3 二次直流等效系统

3.1 不考虑直流干扰条件下接地电阻检测

如图4所示，为接地支路3检测电流波形，波形频率复杂，干扰较强，为了更好地体现直流量对信号干扰的影响，在检测信号中加入幅值为0.05A的，由于直流量影响幅值产生偏移，如图5所示为经旋转变换后z1、z2的检测波形，从波形图中可以看出，理想情况为一直流量的信号产生振荡，影响测量结果值。表1的计算结果表明在未考虑直流信号干扰条件下电阻绝对误差为30.3%，偏离实际值较大，电容值测量绝对误差0.04%与实际值相差较小。

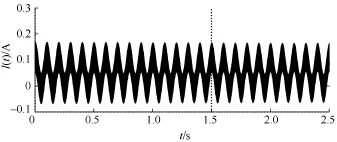
图4 接地支路电流检测波形

图5 经旋转变换后的z1、z1波形

表1 仿真计算结果

3.2 考虑直流干扰条件下接地电阻检测

将采集到的支路电流信号y(t)及电压信号经过u(t)一阶微分处理后，除以注入信号角频率ω再经新的检测算法处理，可有效消除直流分量对检测结果的影响，如图6所示波形为经过一阶微分处理后的电流检测波形，波形以水平轴对称，但增大了其他频率段交流信号幅值。

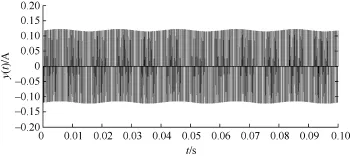
图6 经微分处理后的支路电流波形

图7 所示的为考虑直流干扰条件下经旋转变换后z1、z2的检测波形，z1、z2值分别趋于最终值0.0101A、0.059A，稳定性较好。

图7 考虑直流干扰条件下经旋转变换后的z1、z2波形

表2中数据为考虑直流干扰条件下仿真计算结果，相比表1中数据直流电阻检测误差明显提高，测量绝对误差仅为1.82%，电容值检测与表1中数据相同，表2中仿真计算结果证明直流干扰对信号检测精度影响较大。

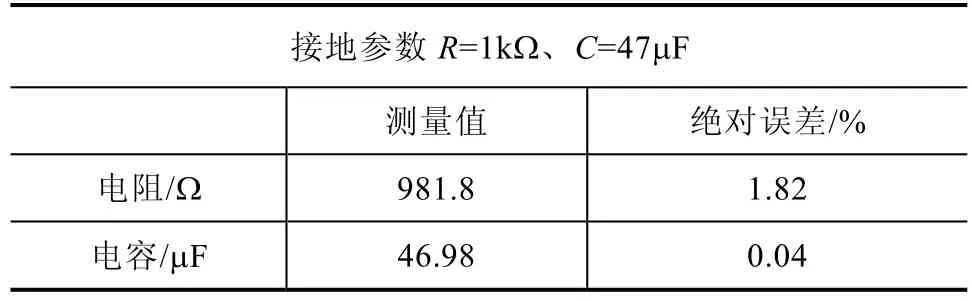
表2 考虑直流干扰条件下仿真计算结果

4 结论

本文提出的基于旋转变换后的二维正弦跟踪器算法的变电站二次直流系统接地故障检测，能够直接提取故障支路接地电阻电流及等效对地电容电流，通过等效电路数学计算，得出的接地电阻值和等效电容值能够全面反映各支路运行状况，为变电站二次直流接地故障检测提供了新思路。该方法抗干扰能力强，检测速度快，在复杂频谱信号条件下准确检测出接地电阻值和等效电容值。仿真结果表明，该方法检测速度快，精度高，有良好的实用价值。

[1] 黄海宏, 陈伟, 王海欣. 多直流支路接地检测方法的研究[J]. 电子测量与仪器学报, 2011, 25(9): 793-798.

[2] 王广柱, 魏殿杰. 直流系统绝缘自动监测仪研制[J].电子测量与仪器学报, 1998, 12(2): 51-54.

[3] 孙鸣, 马娟. 直流系统微机型绝缘监测装置电阻选择[J]. 电力系统保护与控制, 2011, 39(4): 128-131.

[4] 李冬辉, 王金凤, 史临潼. 分形在直流系统故障检测中的应用[J]. 电力系统自动化, 2005, 29(21): 53-56, 84.

[5] 李冬辉, 王波, 马跃贤. 基于小波熵神经网络的直流系统环网接地故障检测[J]. 电力自动化设备, 2008, 28(3): 51-54.

[6] 薛蕙, 杨仁刚. 基于FFT的高精度谐波检测算法[J].中国电机工程学报, 2002, 22(12): 106-110.

[7] 张大波, 刘志刚, 张亚军. 复小波研究现状及其在电力系统中的应用进展[J]. 电力系统自动化, 2006, 30(17): 97-104.

[8] Karimi-Ghartemani M, Ziarani A K. A nonlinear time-frequencyanalysis method[J]. IEEE Transactions on Signal Processing: a Publication of the IEEE Signal Processing Society, 2004, 52(6): 1585-1595.

[9] Karimi-Ghartemanim K, Ziarani A K. Performance characterization ofa nonlinear system as both an adaptive notch filter and a phase-locked loop[J]. International Journal of Adaptive Control Signal Process, 2004, 18(1): 23-53.

[10] 潘学萍, 扈卫卫, 尚霏. 多信号模态参数识别的小波方法[J]. 电力自动化设备, 2013, 33(5): 31-36.

[11] 李冬辉, 史临潼. 基于小波变换的直流系统接地故障检测中小波基的选择与比较[J]. 电力系统及其自动化学报, 2004, 16(6): 48-51, 87.

[12] 储昭碧, 张崇巍, 冯小英. 一种可调带宽的线性电力信号实时分析新算法[J]. 中国电机工程学报, 2009, 29(1): 99.

[13] 储昭碧. 基于自适应陷波滤波器的电力信号时频分析[D]. 合肥: 合肥工业大学, 2009.

[14] 王洪涛, 李天云, 刘辉军. 基于二维线性跟踪器的二次系统直流接地故障检测新方法[J]. 电网技术, 2012, 36(5): 204-208.

The New Method of Detecting DC Circuit Grounding Fault in Power Station Considering DC Interference

Zhu Deliang Su Jianming
(Tongling Power Supply Company，Anhui Electric Power Corporation, Tongling, Anhui 244000)

Linear sinusoidal tractor for specific frequency signals with good amplitude and phase frequency characteristics can be used in detecting DC circuit grounding fault. The method of injecting signal for DC circuit grounding fault affected by branch distributed capacitance. A new method based on improved discrete LST for DC circuit grounding fault in station was presented in this paper. Mathematical model for the equivalent circuit of detection system was given. By rotation transformation of the algorithm for LST, the resistance current and equivalent capacitive current value of alternating current signal can be directly obtained. For a first-order differential treatment, the DC component can be filtered out, adjusting the tractor parameters, specific frequency AC signal under testing separated, according to the grounding resistance and the equivalent capacitance is calculated to give each branch grounding resistance and capacitance, The simulation results show that the algorithm can overcome the effects of stray capacitance and accurately detects grounding fault.

linear sinusoidal tractor; DC circuit grounding fault; first-order differential; rotation transformation

朱德亮（1982-），男，本科，工程师，研究方向为电力系统自动化。