基于分段等效电路法的Litz线绕组损耗求解

徐祥旺 陈 为

（福州大学电气工程与自动化学院，福州 350108）

基于分段等效电路法的Litz线绕组损耗求解

徐祥旺 陈 为

（福州大学电气工程与自动化学院，福州 350108）

为了减小磁性元件的绕组损耗，Litz线备受设计者们的关注，但其庞大的单线股数和复杂的绞制方式使得Litz线的绕组损耗难以计算和仿真。本文从Litz线的绞制方式出发，分析不同绞制方式下Litz线的电流分配特性，并针对业界更普遍使用的同心绞Litz线进行细致分析，提出分段并绕平行线可近似替代同心绞Litz线的想法，并以此为依据使用分段等效电路法求解同心绞Litz线的单线电流，然后将求得的单线电流值重新赋值到2D并绕平行线的仿真模型中进行仿真，即可求解同心绞Litz线的绕组损耗，并在最后验证了分段等效电路法求解同心绞Litz线绕组损耗的有效性和准确性。

绕组损耗；Litz线；电磁场仿真；分段等效电路法

电力电子技术作为高效的功率变换技术，已然成为了绝大多数用电设备不可或缺的电源设计依据。而作为其关键器件的磁性元件，在功率变换电路中担任着能量存储、传递和过滤等职能。随着电力电子技术不断地高频化和高功率密度化的发展，磁性元件的损耗特性成为制约其更新换代的重要因素之一，其中磁性元件的绕组损耗占据着磁件总损耗很大的一部分。

磁性元件的绕组损耗基本上都是由于涡流效应引起的。普通的实心圆导线因为要承载足够高的电流所以其线径必须要足够大，但由于高频交流电流涡流效应的作用将产生远大于直流损耗的涡流损耗，因此为了减小涡流效应带来的损耗，设计者们采用多股较细的单线并绕代替实心圆导线，同时为了避免多股并绕单线之间的内邻近效应所额外带来的涡流损耗，将多股单线进行绞制处理，这就是Litz线的来源。

Litz线有效地降低了涡流效应引起的损耗，但其庞大的单线股数和复杂的绞制方式也使得Litz线的研究出现层层瓶颈，故而Litz线的绕组损耗变得难以计算和仿真，这严重阻碍了Litz线的使用和发展。现今国内外对Litz的研究多不胜举，但大多数都比较片面且包含很多局限性，如文献[1]从Litz线焊点出发，解释其与多股并绕平行线具有相似电流分布的原因，但焊点的影响实际上很小可忽略不计；文献[2]使用等效复数磁导率的方案计算Litz线损耗，但仅限用于复合绞Litz线，而不适用于同心绞Litz线。还有很多纯粹从理论计算出发总结Litz线绕组损耗算法的想法[3-4]，但都有诸多的局限性。

这些算法和思想并没有从根源上解决Litz线绕组损耗的问题。本文将从Litz线的绞制方式出发，分析不同绞制方式Litz线的电流分配特性，并着重针对同心绞Litz线进行研究，然后通过分析分段等效电路法的原理以阐述其对于解决Litz线绕组损耗的可能性，并在最后通过对比三维Litz线仿真和分段等效电路法求Litz线绕组损耗的方案验证了分段等效电路法的准确性和有效性。

1 Litz线的绞制类型与其电流分配特性

根据绞制方式的不同，Litz线大体可分为复合绞Litz线和同心绞Litz线[5]。复合绞Litz线是最理想的Litz线，它先将每根Litz线的所有单线分成多个小组，每组包含少数的单线，然后先将每个小组的单线绞绕，再将这些绞好的导线再重新分组绞绕，经过不断地分组绞绕，最后绞为一个整体即为一根Litz线，如图1所示。由于每组内所有单线已进行绞绕，所以每组内的单线之间是等价的，它们之间几乎不存在内邻近效应，也就是说其阻抗特性一致，而绞好的导线再次分组绞绕，保证了每股单线在同一根Litz线内都是等价的，它们的阻抗特性都保持一致，这使得同一根Litz线内所有单线都被分配相同的电流，最大限度地减小了Litz线的绕组损耗。

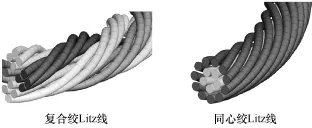
图1 复合绞Litz线和同心绞Litz线

复合绞Litz线对绕组损耗的优化效果毋庸置疑，但其复杂的绞制过程和导线消耗使其成本增高到了一般设计者无法承受的地步，因此宁愿牺牲绕组损耗以换取低成本，所以业界中使用得更普遍的是成本低得多的同心绞Litz线。与复合绞Litz线不同，同心绞Litz线只要经过一次整体的绞制即可，这也使得同心绞Litz线呈现同心圆的分层现象，如图1所示。这种绞制方式最终导致的结果是，处在同一层的单线互相绞绕，而不同层的单线则没有绞绕，所以同心绞Litz线只有同层的单线之间保持阻抗一致，使其电流分配一致，而不同层间阻抗随频率、外磁场等因素变化，电流分配不一致。相较于多股并绕平行线和实心圆导线，同心绞Litz线在很大程度上减小了绕组损耗，但并没有复合绞Litz线的优化程度高，但由于其较低的成本，综合考虑下仍然成为设计者们的首选。

为了验证以上关于不同绞制方式Litz线电流分配特性的分析，取股数为16的复合绞Litz线、同心绞Litz线和多股并绕平行线，使用电磁场仿真软件Ansoft建立相应的绕组模型，将它们置于中柱磁心的气隙附近进行仿真，对每股单线编号并记录其电流值。图2给出了不同导线的3D仿真模型，图3给出了不同导线的单线编号和500kHz频率下的相应电流值，由图3易知，复合绞Litz线的单线电流几乎一致，同心绞Litz线的同层单线电流也几乎一致，而不同层的电流不同，符合以上分析。

图2 不同导线带磁心和气隙的3D仿真模型

图3 不同导线的单线编号和相应电流值

2 分段等效电路法求电流分配的原理分析

无论是复合绞Litz线还是同心绞Litz线，都有较为复杂的绞制方式和场分布特性，因此很难从理论算法的角度出发归纳其理论计算模型。所以相对来说使用电磁场仿真更加准确可靠，但其庞大的单线股数和复杂的绞制方式使得3D仿真模型难以建立和剖分，更别说进行仿真了。然而若想借用2D仿真又不得不考虑如何解决绞制这一2D模型无法实现的过程。对于2D模型，如果导线是多股并绕平行线，由于未进行绞制，所以直接设置并联电流条件即可。而对于复合绞Litz线，因为其每股单线的阻抗特性相等，所以只要设置均分电流条件即可，即每股单线的电流都为Iall/N，Iall为每根Litz线的总电流，N为总股数。当然，因为Litz线经过绞制，长度会比并绕平行线更长，所以2D仿真所得的绕组损耗仿真结果还要乘上一个长度系数。然而，对于同心绞Litz线，以上的电流条件均不适用，也就是说无法单纯地使用电流条件来描述绞制过程，必须先通过其他方案求得每股单线的电流才能进行仿真。

若要求并绕平行线每股单线的电流值，可以使用等效电路法，即从电路的角度出发，将每股单线等效为一个电感，并且单线之间的相互耦合用互感描述，如图4所示。通过这些单线的阻抗参数和电流值即可求得每股单线的总电压，如式（1）所示，而这些单线实际上是呈并联关系的所以总电压相等，可得式（2）所示的方程组，其中Iall为并绕平行线的总电流，由式（1）和式（2）即可求得每股单线的电流值。

图4 并绕平行线的等效电路模型

同心绞Litz线的绞制过程实际上是每一同心层内单线呈圆筒状的绞绕过程，其任意位置的横截面图并未发生很大变化，只有同层的单线间在不断地互换位置，所以每股单线可以简化为由多段同层但不同位置的并绕平行线相互连接而成，而且其分段数即为该层单线的个数。因此，可以用分段并绕平行线来近似替代同心绞Litz线，每股单线的阻抗即为该单线所在同心层的所有并绕平行线阻抗的平均值，相应的每股单线的总电压即为同心层内所有并绕平行线总电压的平均值。显然，同层单线的阻抗相等，故其分配的电流值也相等，而不同层的阻抗随频率和外磁场等因素变化，电流值也不同，完全符合同心绞Litz线的电流分配特性。

将式（1）中并绕平行线的阻抗矩阵简化为式（3），则可得图5所示的同心绞Litz线的等效电路模型，ΣU含义如式（4）所示，对比并绕平行线和同心绞Litz的等效电路模型，Ui表示第i位置的并绕平行线的总电压，Ui′表示第i位置的同心绞Litz线的总电压，同样的Ii表示第i位置的并绕平行线电流，Ii′表示第i位置的同心绞Litz线电流，Nk为第k层的单线股数，N为总股数，C为其层数。

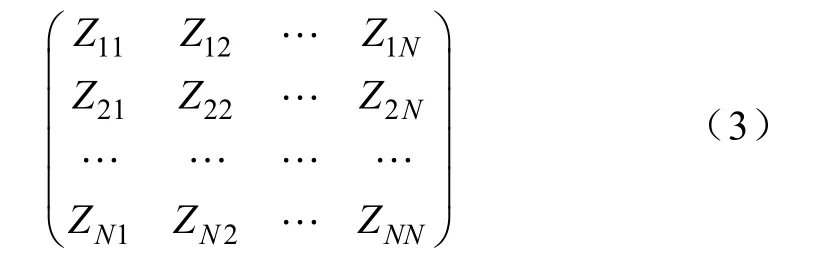
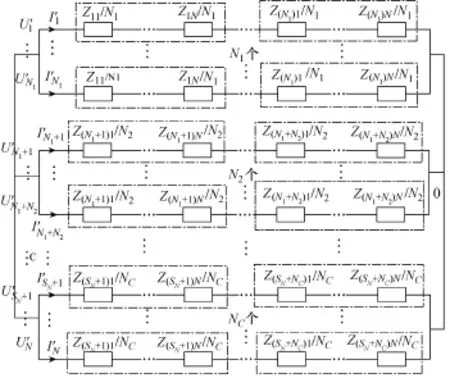
图5 同心绞Litz线的等效电路模型

因为同层单线的总电压和电流都相等，所以可用ULi表示第i层同心绞Litz线的单线总电压，同样用ILi表示第i层同心绞Litz线的单线电流，即如式（5）和式（6），则同心绞Litz线的阻抗矩阵如式（7），因为同层单线的阻抗、电流和电压都相等，所以式（7）可以简化为式（8），即将N*N的矩阵简化为C*C。同样的，同心绞Litz线的所有单线实际上是呈并联关系的所以单线总电压也相等，可得式（9），由式（9）、式（8）和式（3），即可求得同心绞Litz线所有单线的电流分配值。该方法可以简称为分段等效电路法。

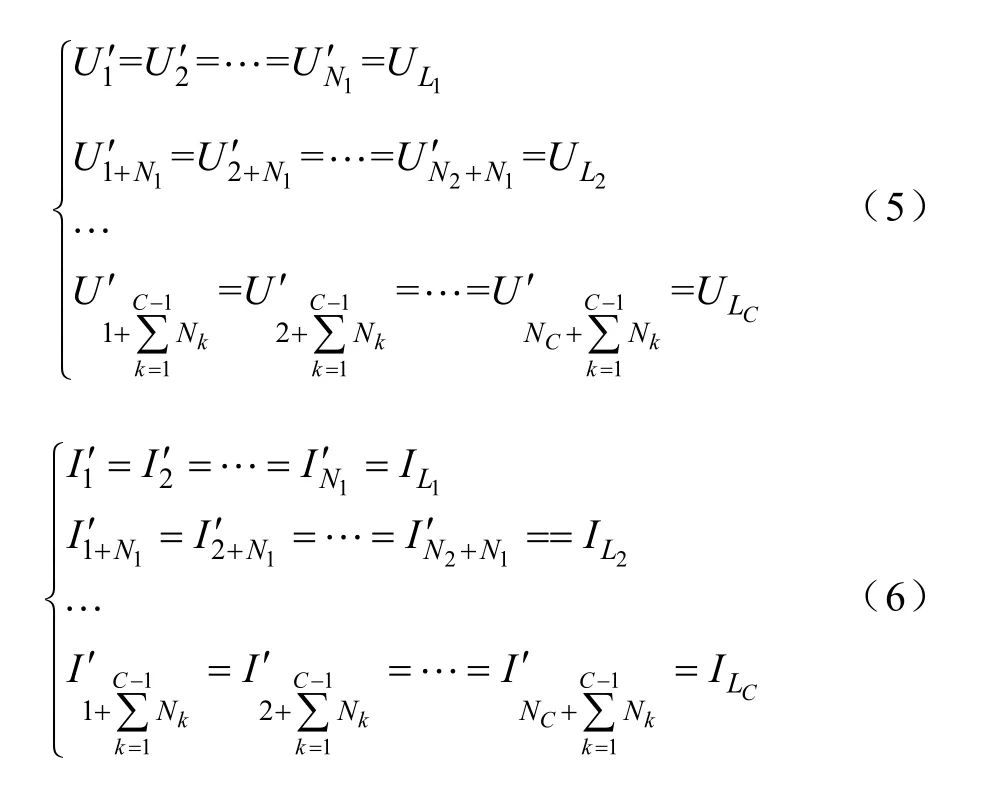
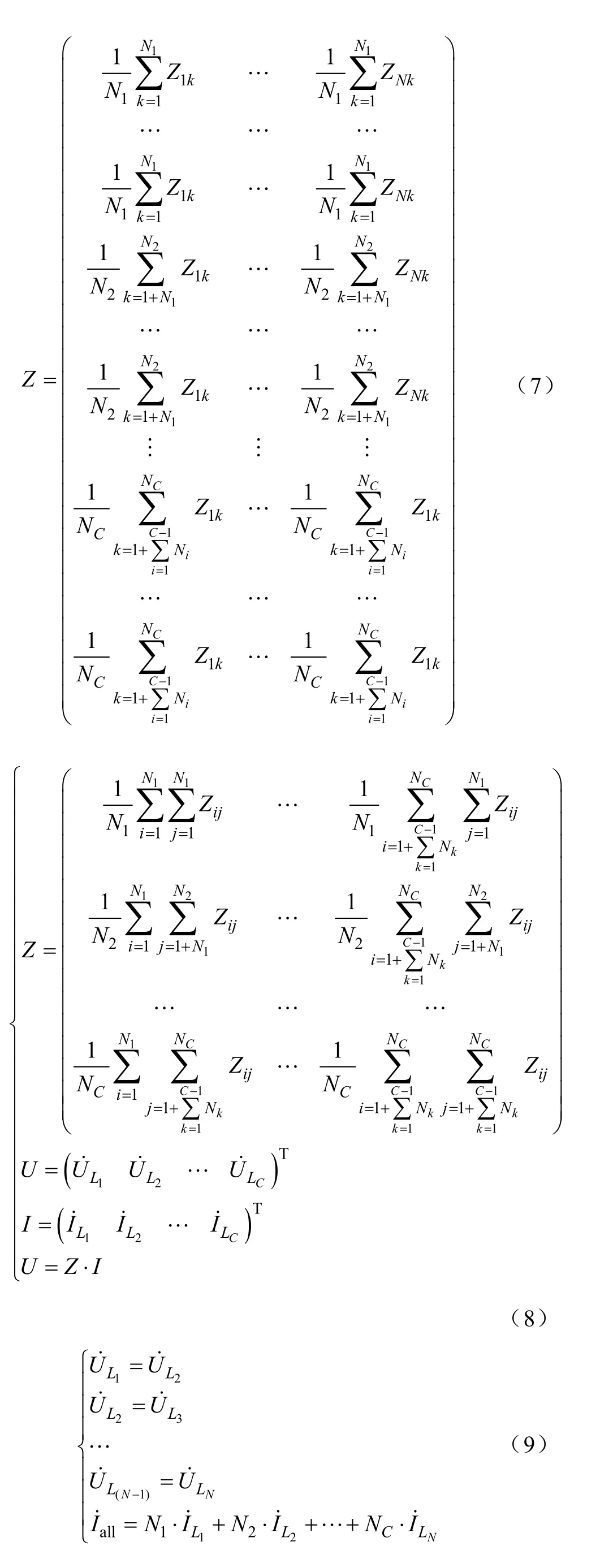
由2D并绕平行线模型仿真出单线间的耦合阻抗Z阵即式（3），然后将其代入到式（8）和式（9）中求得同心绞Litz线每层单线的电流值，再将电流值重新赋值到2D并绕平行线模型中进行绕组损耗仿真，其结果即为同心绞Litz线的绕组损耗。以上讨论的皆为单匝Litz线的单线电流计算公式，同样可以很容易地扩展到多匝Litz线的电流计算公式中，但受篇幅限制，这里不再赘述。

3 仿真验证

为了验证分段等效电路法的准确性，本文以3D同心绞Litz模型的绕组损耗仿真为基准，分别对2D并绕平行线模型设置均分电流、并联电流和由分段等效电路法求得的电流，并进行绕组损耗仿真，Litz线的股数为16，分两层，里外层单线数分别为5和11。图6给出了同心绞Litz线的3D模型和并绕平行线的2D模型。图7给出了500kHz下3D同心绞Litz线模型的各单线电流仿真结果和用分段电流法所求得的结果，横坐标为单线序号，其中分段电流法所需要的Z阵即由并绕平行线2D模型仿真得到。图8给出了各模型的绕组损耗和以3D模型绕组损耗仿真结果为基准的相对误差图，横坐标为频率，总激励电流幅值为1A。

图6 3D同心绞Litz线模型和2D并绕平行线模型

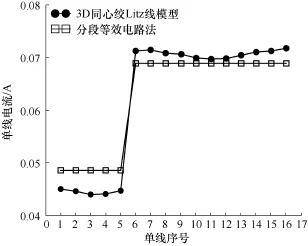
图7 各模型的单线电流值

图8 各模型绕组损耗和相对误差图

由图7易知，由分段等效电路法求得的单线电流值与3D同心绞Litz线模型的仿真结果几乎相等。而由图8易得，使用均分电流和并联电流的2D并绕平行线仿真作为Litz线的仿真结果都会带来很大的误差，而使用分段等效电路法所求得电流的绕组损耗仿真的误差都在5%以内，足以满足工程的需求，由此可证明分段等效电路法的准确性和有效性。

4 结论

本文通过对不同绞制方式下Litz线的电流分配特性进行研究，提出并细致分析了分段等效电路法的原理和其对于同心绞Litz线绕组损耗计算的有效性，并在最后进行验证，得出结论如下：

1）复合绞Litz线每股单线的阻抗特性几乎一致，所以每股单线的电流值基本相同，可直接通过对并绕平行线设置均分电流条件进行2D模型仿真。

2）同心绞Litz线呈同心圆的分层现象，同层单线阻抗特性几乎一致，不同层则不同，同层单线电流基本相同而不同层受频率和外磁场等因素影响，因此无法通过简单的电流条件设置以进行仿真。

3）对于同心绞Litz线可以先通过分段等效电路法求得单线电流，然后赋值给并绕平行线，即可进行2D模型仿真解决同心绞Litz线绕组损耗无法求解的问题，该方案已通过仿真实验验证，与3D同心绞Litz线绕组损耗仿真相比误差在5%以内，具有足够高的精度。

[1] A Roßkopf EB, Joffe C. Influence of inner skin-and proximity effects on conduction in Litz wires[J]. in IEEE Transactions on Power Electronics. Oct, 2014, 29(10): 5454-5461.

[2] Sullivan R. An equivalent complex permeability model for Litz-wire windings[C]//Industry Applications Conference, 3, 2005: 2229-2235.

[3] Eit M Al, Bouillault F, Marchand C, et al. 2-D Reduced Model for Eddy Currents Calculation in Litz Wire and Its Application for Switched Reluctance Machine[J]. in IEEE Transactions on Magnetics, 2016, 52(3): 1-4.

[4] Bartoli M, Noferi N. Modeling litz-wire winding losses in high-frequency power inductors[J]. IEEE PESC'96, 1996, 27(2): 1690-1696.

[5] 周自云. 偏转线圈用利兹(Litz)线的工艺研究[C]//中国电器工业协会电线电缆分会2005年绕组行业“十一•五”发展研讨会, 2005: 100-106.

Solution of Litz Wire Winding Loss based on Segmented Equivalent Circuit Method

Xu Xiangwang Chen Wei
(College of Electrical Engineering and Automatic, Fuzhou University, Fuzhou 350108)

In order to reduce the winding losses of magnetic components, Litz wires brought designers into sharp focus. But its large strands and complex twisting mode makes the winding loss of Litz wires difficult to calculate and simulate. This paper from twisting mode to analysis the current assignment characteristics of different twisting mode of Litz wires, and particularly analysis the concentric twisted Litz wires which is more widespread used in the industry. The thought is proposed that concentric twisted Litz wires can be approximately replaced by segmented stranded parallel wires, and the single wire current of concentric twisted Litz wires can be solved by using the segmented equivalent circuit method based on this thought. Reassignment the single wire current value to 2D stranded parallel wires model for simulation, and then the winding loss of concentric twisted Litz wires can be solved. Finally, it is proved that the segmented equivalent circuit method is effective and accurate for solving the concentric twisted Litz wire winding losses.

winding loss; Litz wires; simulation of electromagnetic field; segmented equivalent circuit method

徐祥旺（1991-），男，福建南平人，硕士研究生，研究方向：电力电子高频磁技术。