双晶压电悬臂梁俘能器的建模与仿真*

王新掌， 郝少帅， 许孝卓， 李红磊

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

双晶压电悬臂梁俘能器的建模与仿真*

王新掌， 郝少帅， 许孝卓， 李红磊

(河南理工大学 电气工程与自动化学院，河南 焦作 454000)

针对双晶片悬臂梁式压电俘能器的优化问题，考虑悬臂梁末端位移与质量块质心位移的差异，对Roundy数学模型进行了修正。通过ANSYS有限元软件对俘能器建模并进行模态分析和谐响应分析，当质量块长度逐渐变大时，修正后数学模型对俘能器一阶固有频率和输出电压有更好的预测精度。研究了质量块形状和负载对俘能器输出特性的影响规律，发现在质量块质量不变时，提高质量块的质心高度能提高俘能器的发电能力，对俘能器的结构优化具有借鉴意义。

悬臂梁； 压电俘能器； ANSYS； 谐响应分析

0 引 言

压电振动俘能器是利用压电陶瓷的正压电效应来实现机械能向电能转换，与其它形式如电磁式、静电式[1]振动俘能器相比，具有结构简单、体积小、成本低及能量密度大等优点，在军事、医疗和建筑等领域已开展了相关的研究[2～4]。

为了对振动式压电发电机进行优化设计，国内外Roundy S[5],Erturk A[6],Kim M[7],贺学锋等人[8]对悬臂梁式微型压电振动能采集器的理论模型已经开展了一些研究。另外，朱波[9]、龚俊杰[10]和姜德龙等人[11]通过仿真和实验分析了压电层和金属层厚度、长度以及质量块质量大小对俘能器输出特性的影响规律，而在保持质量块质量不变前提下，只改变质量块形状对俘能器输出特性的影响却很少有分析。

针对双晶压电悬臂梁式俘能器的集总参数模型，由于Roundy S等人[5]忽略了悬臂梁末端位移与质量块质心位移的差异，导致在质量块与梁长度相当时，模型有较大的误差。本文在Roundy模型的基础上，考虑了质量块质心位移与悬臂梁末端位移的差异，建立了修正后的数学模型，并利用ANSYS有限元分析软件建模对Roundy模型和修正后的模型的结果进行对比，同时,研究了质量块长度以及当质量块质量不变时质心高度对俘能器一阶固有频率、电压及功率输出的影响规律，为悬臂梁压电俘能器的优化设计提供一定的指导。

1 悬臂梁压电俘能器理论模型

典型的压电双晶悬臂梁结构如图1 所示，金属层的上下面表面都贴有压电陶瓷，固定端固定于基座中，梁的自由端附有质量块。

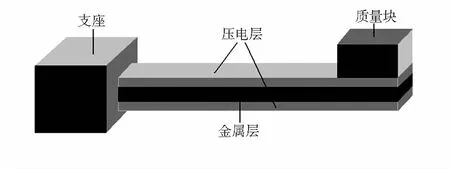
图1 压电双晶悬臂梁结构

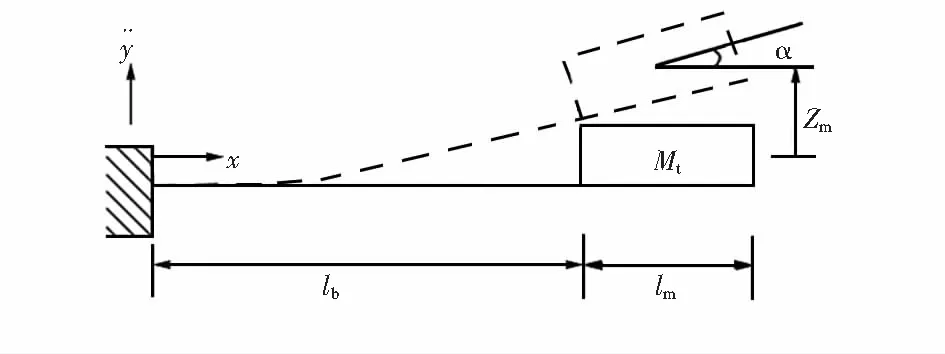
图2 数学模型

将俘能器简化为一个弹簧—质量块单自由度系统。

根据材料力学，梁的等效惯性矩为

(1)

式中b=(tc+tsh)/2，ηs=csh/cp；csh与cp分别为金属层和压电层的弹性系数。

距固定端距离为x处的悬臂梁弯矩为

(2)

根据欧拉—伯努利梁方程，梁挠度方程为

(3)

取x=lb，积分求得悬臂梁末端挠度

(4)

考虑悬臂梁末端位移与质量块质心位移的差异，这里忽略质量块变形，将其简化为一个理想刚性体，因此,质量块转角与悬臂梁自由端转角相同,则质量块质心挠度为

(5)

由压电层内的平均应力

(6)

压电片应力与应变关系

σ=cpS

(7)

解得

(8)

zm=k2S

(9)

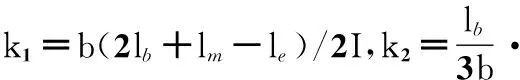
那么，悬臂梁的等效刚度为

(10)

系统的固有频率为

(11)

俘能器的等效电容为

(12)

式中ε为压电材料的介电常数；当双晶压电片串联时a=1，并联时a=2。

系统在幅值为Ain、频率为ω的加速度外加激励下，在压电片两级加电阻负载R，最大输出电压为

(13)

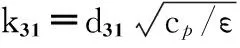
当激励频率与系统固有频率相等，即ω=ωn时，输出电压为

(14)

电阻负载下的等效输出功率为

(15)

上式对R求导，得最优电阻负载为

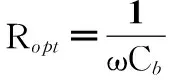
(16)

从式(14)可看出，压电俘能器的电压输出受到外激励大小以及其结构尺寸、压电转换系数和压电耦合系数的影响。

从式(5)中可以看出:当lm≪lb，即质量块长度相对于金属基板长度很小时，可以近似用悬臂梁末端位移代替质量块质心位移；质量块长度与金属基板长度相当或者差别不大时，悬臂梁末端位移代替质量块质心位移会产生很大误差。

2 数值计算与ANSYS仿真分析

为了使悬臂梁承受更大的形变，选用韧性较大的磷青铜为基板，质量块采用磷青铜，压电陶瓷采用PZT—5H。

根据表1的材料参数和结构参数运用有限元分析软件ANSYS对双晶压电悬臂梁进行耦合场分析。压电片端为固定端，质量块端为自由端，对系统进行模态分析，得到系统的固有频率。然后，在悬臂梁固定端施加加速度幅值为0.2 gn(1 gn=9.8m/s2)，激励频率为系统的固有频率的正弦激励，通过谐响应分析得到系统的电压—频率响应曲线。

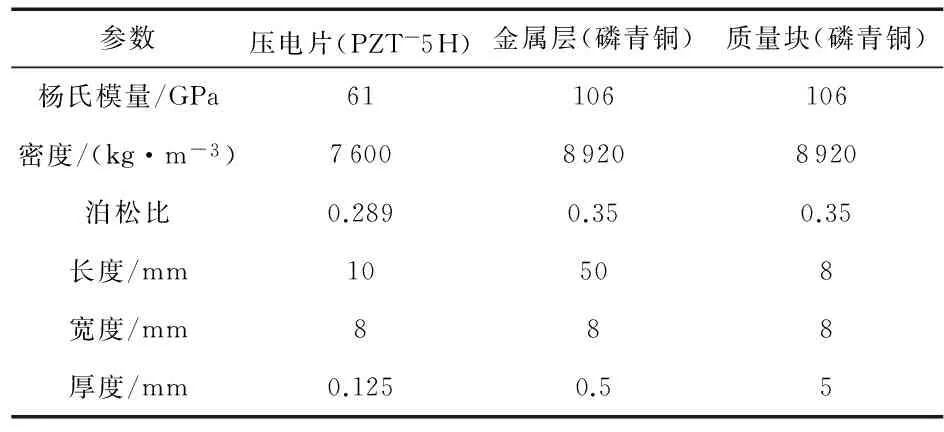
表1 压电悬臂梁参数表

2.1 质量块长度对频率和电压影响

固定金属基板和压电片的尺寸不变，仅改变质量块的长度，通过数值计算，得到系统开路情况下的固有频率、输出电压与质量块长度的关系。

由图3可看出，双晶串联和并联的固有频率相等，并且随着质量块长度的增加而变小；图4则表明双晶串联时的输出电压是并联时的2倍，并随着质量块长度的增加而变大。由于质量块的厚度和宽度不变，随着长度的增加，质量块的质量也跟着线性增加，所以也可以得出结论：增加质量块的质量可以有效降低系统的固有频率，同时也提高了系统的输出电压。

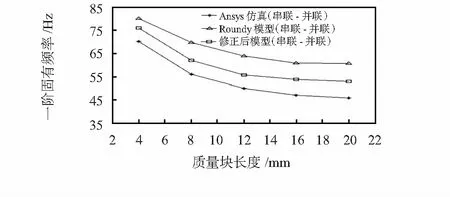
图3 频率与质量块长度关系

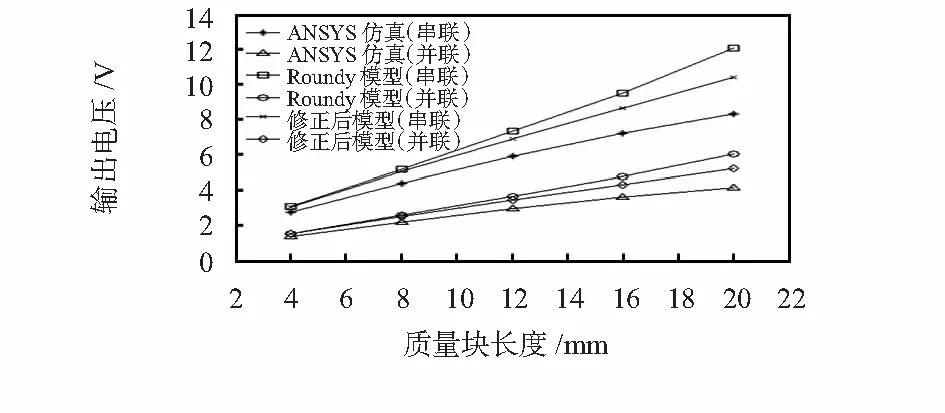
图4 输出电压与质量块长度关系

表2为两种数学模型的计算结果与ANSYS仿真结果的对比，其中,η1,η2分别为Roundy模型和修正后模型的频率相对于ANSYS仿真的误差，μ1,μ2分别为Roundy模型和修正后模型的输出电压相对于ANSYS仿真的误差。从表2中可以看出，随着质量块长度的增加，Roundy模型对仿真结果的误差越来越大，而修正后模型相对于仿真结果的误差要小许多，说明修正后的数学模型提高了对俘能器性能的预测精度，能更好地对俘能器性能进行预测。

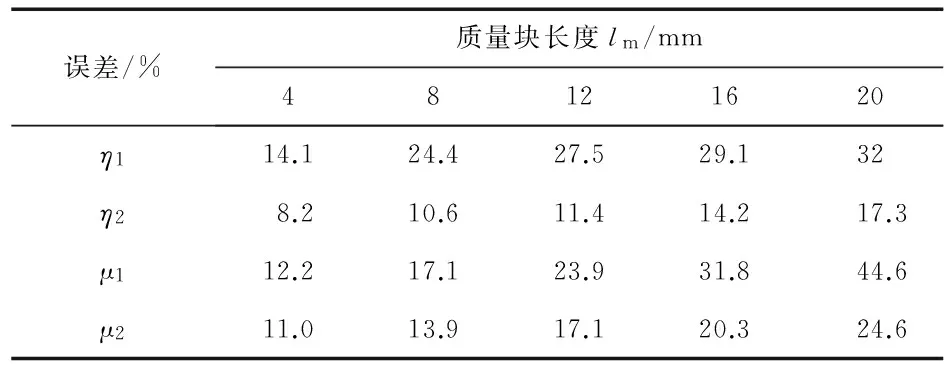
表2 两种模型结果相对于ANSYS仿真的误差

2.2 质量块质心高度对频率和电压的影响

在保持质量块质量和宽度不变的情况下，分析质量块质心高度与俘能器频率和输出电压的关系。图5为质量块宽度为8 mm，长(mm)×厚(mm)分别为20×2,16×2.5,12×3.3,8×5和4×10，也即质量块质心高度Hc分别为1,1.25,1.65,2.5,5 mm下双晶片串联条件下的频率—电压曲线。其中，质心高度由1 mm升高到5 mm时，一阶固有频率由68.167 Hz变为52.065 Hz，降低了23.6 %；输出电压由3.94 V变为4.54 V，升高了15.2 %。因此，在对系统整体质量有限制的情况下，可优先考虑选用质心高的质量块来降低固有频率的同时提高俘能器的电压输出。

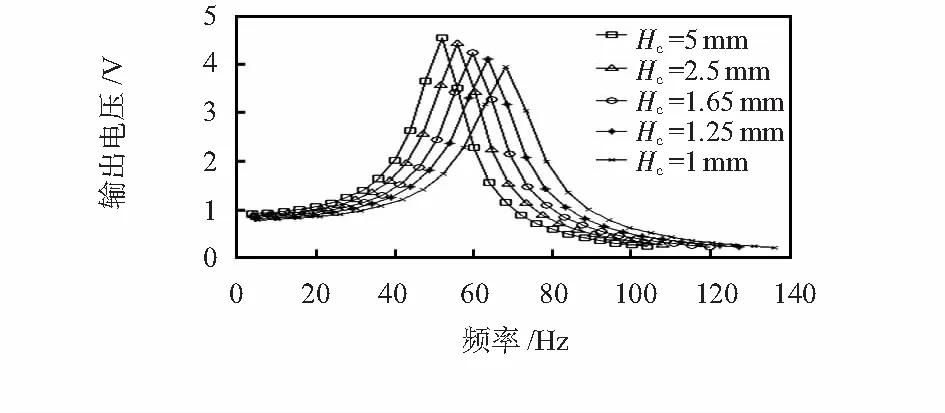
图5 质量块质心高度对频率—电压曲线的影响

2.3 负载对俘能器输出的影响

在双晶片串联前提下，分析了不同电阻负载对俘能器电压、功率的影响。图6为电阻从0.25 MΩ到2 MΩ不同取值下对应的电阻两端电压和功率曲线，俘能器结构尺寸如表1所示。从图6中可以看出，随着外加电阻不断增大，俘能器输出电压不断升高，而功率则是先增大后减小，在0.75 MΩ时功率最大，与式(16)理论计算得出的0.95 MΩ误差为26.7 %，验证了数学模型的正确性。

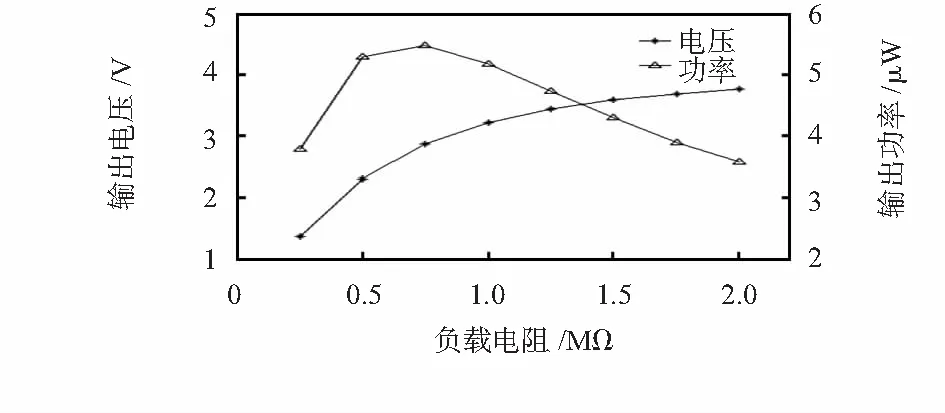
图6 负载电阻与电压、功率曲线

3 结 论

1)在考虑质量块中心挠度与悬臂梁末端挠度的差异下，修正后的数学模型对俘能器性能有更准确的预测，对压电悬臂梁式俘能器的结构优化具有指导意义。

2)增加悬臂梁末端质量块的质量，能有效提高俘能器的发电能力，同时也可有效地降低俘能器的固有频率。另外，在质量块质量一定的前提下，提高质量块质心高度更有助于俘能器发电性能提高。

3)通过数学分析和仿真分析得出，在俘能器装置确定的情况下，负载对俘能器的发电性能也有影响，要使输出功率最大，需要匹配最优负载。

[1] Sidek O,Khalid M A,Ishak M Z,et al.Design and simulation of SOI-MEMS electrostatic vibration energy harvester for micro power generator[C]∥Proceedings of the 1st International Conference on Electrical,Control and Computer Engineering,2011:207-212.

[2] Lefeuvre E,Badel A,Richard C,et al.A comparison between several vibration-powered piezoelectric generators for standalone systems[J].Sensors and Actuators A:Physical,2006,126(2):405-416.

[3] 陈丽娟,许晓慧,吴在军,等.无线传感器网络的节点能量自供给方法[J].振动、测试与诊断,2012,32(6):994-998.

[4] Park J C,Lee D H,Park J Y,et al.High performance piezoelectric MEMS energy harvester based on D33 mode of PZT thin film on buffer-layer with PBTIO3inter-layer[C]∥2009 Solid-State Sensors,Actuators and Microsystems Conference,2009 International Transducers Conf on Transducers，IEEE,2009:517-520.

[5] Roundy S,Wright P K.A piezoelectric vibration-based generator for wireless electronics[J].Smart Materials & Structures,2004,13(5):1131-1142.

[6] Erturk A,Inman D J.An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations[J].Smart Materials & Structures,2009,18(2):1282-1294.

[7] Kim M,Hoegen M,Dugundji J,et al.Modeling and experimental verification of proof mass effects on vibration energy harvester performance[J]. Smart Materials & Structures,2010,19(4):45023-45043.

[8] 贺学锋,杜志刚,赵兴强,等.悬臂梁式压电振动能采集器的建模及实验验证[J].光学精密工程,2011,19(8):1771-1778.

[9] 朱 波,刘文波.双晶悬臂梁式压电换能器建模与结构参数分析[J].传感器与微系统,2013,32(5):38-40.

[10] 龚俊杰,许颖颖,阮志林,等.双晶悬臂梁压电发电装置发电能力的仿真[J].振动：测试与诊断,2014,34(4):658-663.

[11] 姜德龙,程光明,曾 平,等.悬臂梁双压电晶片振子发电性能研究[J].机械设计与制造,2011(1):121-123.

Modeling and simulation of bimorph cantilever piezoelectric energy harvester*

WANG Xin-zhang, HAO Shao-shuai, XU Xiao-zhuo, LI Hong-lei

(School of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo 454000,China)

To solve the optimization problem of bimorph cantilever piezoelectric energy harvester,the Roundy mathematical model is modified,where difference between the deflection at the center of the proof mass and that at the end of the cantilever is considered.By using the finite element software of ANSYS，modal analysis and harmonic response analysis of energy harvester model are carried out.The results show that modified model is more accurate than Roundy model in predicting the first order natural frequency and output voltage of the harvester when the length of mass block grows.Influence law of mass block shape and load on energy harvester output characteristics is studied,it is found that when the weight of mass block is constant,mass block with a higher center of mass will make the energy harvester have a better generating capacity,and the result has reference significance for structural optimization of the piezoelectric energy harvester.

cantilever beam; piezoelectric energy harvester; ANSYS; harmonic response analysis

10.13873/J.1000—9787(2017)04—0015—04

2016—03—28

国家自然科学基金资助项目(U1504506,61074095)

TM 282

A

1000—9787(2017)04—0015—04

王新掌(1969-)，男，博士，副教授，主要从事电磁场理论及其应用等方面的研究工作。