保险产品设计方案的数学模型

张金战

(陇南师范高等专科学校，甘肃 成县 742500)

保险产品设计方案的数学模型

张金战

(陇南师范高等专科学校，甘肃 成县 742500)

在保证保险公司不盈不亏的前提下，利用等比数列的求和公式，建立了月保险费a，交纳年限n，固定工资b，死亡年限m及银行利率c之间的指数模型。利用已知数据和MathType公式编辑器、Excel等工具软件给出了在a，n，m，c已知的情况下，b的计算公式及b的值。确定了n和m的关系式，用Excel工具对m，n的值进行了计算，并用Excel作图工具做出了m与n的关系图。

指数模型；对数模型；等比数列;复利

1 问题的提出

某保险公司拟设计一个新的保险产品。设计方案的总体思路是：投保人从一出生开始，每月交纳固定费用a元，交满n年(n是正整数)停止缴费，并从下一月开始按月领取固定额度的工资b元,直至投保人死亡。已知银行月利率为c，一直不变。保险公司只将投保人的缴费及时存入银行，不进行其它投资。

问题1:假设投保人恰好满m岁死亡(m为正整数)，保险公司不盈不亏，试建立常数a，b，c，m，n的关系式，并尽量简化。

问题2:在问题1中，假设a=1000元，n=20年，m=80岁，c=0.25%，求b的值。并写出所用计算工具及操作步骤。

问题3:在问题1中，假设a=1000元，b=2000元，c=0.25%，求m,n的关系式，并用图表或表格形象描述m,n的关系。

问题4：要完成本产品的最终设计，需要哪些数据？并探讨获取和加工数据的有效方案。

2 模型的假设及符号说明

为了简化模型，便于讨论和计算，现对模型中的变量和符号进行说明，并做一些合理的的假设，如下所示：

(1)模型的假设

1)投保人交满n年保险金，并在第m年(m>n，m、n为正整数)死亡，投保人除了按月领取b元固定工资外，保险公司不另行其他赔偿；

2)月份按自然月计算，不分大月和小月，也不考虑闰年；

3)保险公司每月将投保人的保险金及时存入银行；

4)银行的存款利息按复利计算，即银行在每月月底结息，并自动滚入下一月，作为下一月的本金；

5)投保人交满n年保险金后，从n+1年起每月领取固定工资b元。

(2)符号说明

a表示投保人每月交纳的保险金(单位：元)；

b表示投保人在交费期满后每月领取的固定工资(单位：元)；

n表示投保人交纳保险金的年限(单位：年)；

m表示投保人死亡的年限(单位：年)；

c表示银行利率。

3 模型的建立与求解

(1)问题1的解答

1)投保人n年共交纳的保险金本利和的计算

我们可以对投保人n年所交费用与银行所产生的利息的总金额进行分析，具体分析如下：

投保人每月交纳固定费用a元，所交总月份为12n，银行的月利率为c，设到第p个月时，投保人所交保险金的本利和为Ap,(p=1,2，…,12n),则

A1=a

A2=a(1+c)+a

A3=[a(1+c)+a](1+c)+a=a(1+c)2+a(1+c)+a

…

2)投保人交满n年保险金后，从第n+1年起每个月领取固定工资b元直至投保人第m年死亡，设从投保人缴费期满领取工资后的第t个月剩余金额为Bt(t=1，2，3，…，12(m-n)),则有

B1=A12n(1+c)-B

B2=[A12n(1+c)-b](1+c)-b=A12n(1+c)2-b(1+c)-b

…

Bt=A12n(1+c)t-b(1+c)t-1+…-b=A12n(1+c)t-b[(1+c)t-1+(1+c)t-2+…+(1+c)+1]

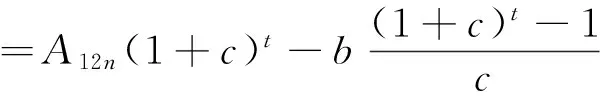
从而有：

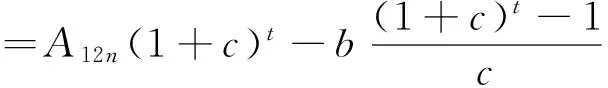
所以

要使保险公司不盈不亏，则有投保人满m岁死亡时剩余金额为0元，即投保人领完第12(m-n)月的工资b元后剩余金额为0元，具体列式如下:

B12(m-n)=0。

即

从而有：

a[(1+c)12n-1](1+c)12(m-n)=b[(1+c)12(m-n)-1]，a(1+c)12n(1+c)12(m-n)-a(1+c)12(m-n)=b(1+c)12(m-n)-b。

即有：

a[(1+c)12m-(1+c)12(m-n)]-b[(1+c)12(m-n)-1]=0

(1)

即假设投保人恰好满m岁死亡(m>n,m，n均为整数)，保险公司不赢不亏，可建立关于a、b、c、m、n的关系式为:

a[(1+c)12m-(1+c)12(m-n)]-b[(1+c)12(m-n)-1]=0。

(2)问题2的解答

在问题1中，假设a=1000元，n=20年，m=80岁，c=0.25%，欲求b的值。

由问题1中得到的关于a、b、c、m、n的关系式(1)式

a[(1+c)12m-(1+c)12(m-n)]-b[(1+c)12(m-n)-1]=0

可得，

(2)

在Excel中，将c,m,n,a的值分别输入到单元格A2，B2，C2，D2中，并在E2单元格中将关系式(2)式用公式输入，其中(1+c)12m和(1+c)12(m-n)利用POWER函数(乘幂函数)，这时在公式栏显示的公式为：

=((POWER(1+A2,12*B2)-POWER(1+A2,12*(B2-C2)))/(POWER(1+A2,12*(B2-C2))-1))*D2。

表1 利用Excel计算b值

按回车键即在单元格E2显示出计算出的b值，即

b=983.7302(元)。

(3)问题3的解答

在问题1中，假设a=1000元，b=2000元，c=0.25%，求m,n的关系式。

对问题1中得到的关系式(1)进行化简，有

a[(1+c)12m-(1+c)12(m-n)]=b[(1+c)12(m-n)-1]，

a(1+c)12m-a(1+c)12(m-n)=b(1+c)12(m-n)-b，

(a+b)(1+c)12(m-n)=a(1+c)12m+b。

对两边分别取对数，有：

lg(a+b)(1+c)12(m-n)=lg[a(1+c)12m+b]，

lg(a+b)+12(m-n)lg(1+c)=lg[a(1+c)12m+b]，

12(m-n)lg(1+c)=lg[a(1+c)12m+b]-lg(a+b)，

于是得m与n的关系式：

(3)

在Excel中，将m(单位：年)的取值输入到单元格Ai(i=2,3,…,80,…)中，并将上面得到的关系式(3)式用公式输入到单元格B2中，其中a=1000,b=2000,c=0.25%。这时在公式栏显示的公式为：

=A2-(LOG10(1000*(1.0025)^(12*A2)+2000)-LOG10(3000))/(12*LOG10(1.0025))。

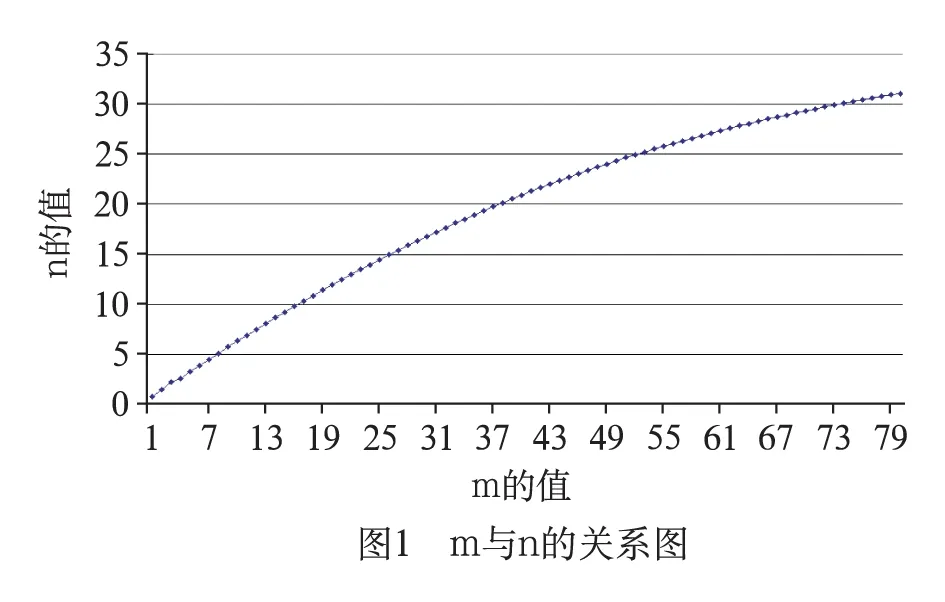
利用Excel计算工具计算出与m所对应的n值，再用Excel的作图功能作出m与n的关系图，如图1所示。

(4)问题4的解答

要完成该保险产品的最终设计，需要确定出投保人月交纳费用a，交纳年限n,交费期满后保险公司按约定应付给投保人的保险工资b，银行利率c是相对确定的，投保人领取保险工资的年限m在进行产品设计时也是应当考虑的重要因素。

a,b,n,m的值是相互制约的，从投保人的角度来看，a值和n值越小越好，但a值小就意味着将来的保险工资b值低，投保人不划算；a值和n值过高，虽然保险工资b值会相应提高，但投保人在经济上难以承受。从保险公司的角度看，当然希望a,n的值高一些，b值低一些，但这又是投保人所不能接受的。因此，确定a,b,n,m的值需要综合考虑。

①a值的确定

a值就是投保人每月向保险公司应交纳的费用。要确定合理的a值，需要考虑一定范围内投保人的收入情况、投保人的参保意识、投保人的保险收益以及保险公司的收益等多种因素，其中收入情况是需要参考的重要因素。另外还需考虑保险费用a占收入的百分比。

②n值的确定

n值就是投保人向保险公司交纳费用的年限。由问题3中得到的n,m之间的关系式，n的值一般依赖于a,b,m,c的取值，在确定了a,b的条件下可以设置合理的n值。

③b值的确定

b值就是保险公司向投保人每月应返还的保险工资。b值同样依赖于a，n,m的值。在a，n一定的条件下，m越大，b值应越小。

④m值的确定

m实际上就是投保人的寿命。确定m值最简单的方法就是考虑人们的平均寿命，把它作为m的一个参考值。

在具体进行保险产品设计时，一般应先确定一个合理的a值，再确定一个预期的m值，然后可以根据问题1中得到的a,b,n,m,c的关系式，利用Excel工具或Mathcad软件进行计算，由此确定b和n的值。

4 对模型的分析

保险产品的设计是一个比较复杂的系统工程，与经济发展水平、人们的消费观念、保险意识、投保人的预期以及保险公司的利益相联系，需要综合考虑。本模型仅是在不考虑其它例外情况的条件下，只保证保险公司不盈不亏时得到的a,b,n,m,c的关系式，并利用Excel工具得到了m与n之间的关系图(见图1)。该模型对保险公司设计保险产品具有一定的参考作用。但其缺陷是所考虑的情形比较简单，因素较单一，因而不能完全地反映社会对保险业的需求，需要可根据一定的限制条件对模型进行相应地改进。

[1] 杨启帆,康旭升,赵雅囡.数学模型[M].北京:高等教育出版社,2005.

[2] 杨启帆,李浙宁,等.数学建模案例集[M].北京:高等教育出版社,2006.

[3] 赵静,但琦.数学建模与数学实验[M].北京:高等教育出版社,2003.

[4] 宋金珂,孙壮,许小重,等.计算机应用基础[M].北京:中国铁道出版社,2005.

[5] 刘玉琏,傅沛仁,等.数学分析[M].北京:高等教育出版社,2003.

The Mathematical Model of Insurance Product Design

ZHANGJin-zhan

(LongnanTeachersCollege,Chengxian742500,China)

Under the premise that the insurance company does not break, using the summation formula of geometric progression, the exponential model is established between monthly premium(a), payment term(n), fixed salary(b), age of death(m) and bank rate(c). Using known data and MathType formula editor, Excel, etc, under the condition that a, n, m and c are informed and b's calculation formula and value, try to determine the relationship between N and M, and the value of M and N is calculated by using the Excel tool.

index model; logarithm model; geometric sequence; compound interest

2016-10-28

张金战(1965-)，男，教育硕士，陇南师范高等专科学校副教授，研究方向：基础数学教学。

O143

A

1674-3229(2017)01-0089-03