一道概率统计试题的分析与教学思考

吕书龙 刘文丽 梁飞豹 陈凤德

（福州大学数学与计算机科学学院，福建 福州 350116）

一道概率统计试题的分析与教学思考

吕书龙 刘文丽 梁飞豹 陈凤德

（福州大学数学与计算机科学学院，福建 福州 350116）

文章通过分析数理统计中一道综合题的多种解法，探讨学生掌握基本概念和应用知识的学习能力层次。并把学习能力层次分成理解偏差型、基本型、理解应用型和融会贯通型四种渐进层级，同时指出分层教学的必要性，并结合作业反馈机制给出合理的教学建议以便为教与学的顺利开展提供一种思路。

数理统计；认知能力；分层教学；作业反馈

1 引言

数学是一门“思而知之”的学科，数学学习的核心在于培养学生解决数学问题的能力，而且数学在对学生的思维训练方面具有其他任何学科无法替代的功能。文献［1］从一类问题的解法角度分析了学生学习和创新能力的培养。文献［2，3］结合分层教学阐述了学生能力培养的重要性。文献［4，5］提到基于问题驱动、任务驱动、反例教学法和情景教学法等来培养学生分析和解决问题的能力。文献［6］阐述了数学思维训练与各种能力培养的关系。大部分文献缺少对能力层次进行细分，也较少涉及对能力层次动态变化的跟踪。众所周知，学生各项能力的差异对教学将产生直接的影响。当下，基础课教学课时常被压缩，在教学过程中及时把握学生学习能力层次变化,适时地调整教学模式已成为因材施教和分层教学的关键。

“概率论与数理统计”作为一门本科阶段全校性的公共基础课,已多年实行教考分离，统考统改。在教学改革上也做了很多工作。但在划分学生学习能力层次以及如何评价学生掌握知识和综合应用水平方面，工作还比较欠缺，有待完善。本文通过“概率论与数理统计”中一道综合题的多种解法尝试将学生的学习能力层次划分为：理解偏差型、基本型、理解应用型和融会贯通型四种类型，并对其进行合理分析，旨在为分层教学［2，3］的推进提供一种测度参考，也为课程的多层次综合考核与评价提供一种思路。

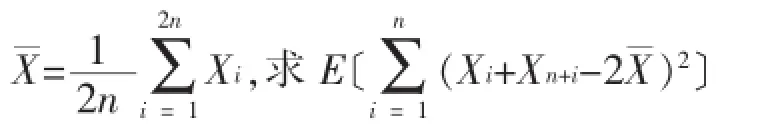
这是一道综合了数学期望、独立同分布样本和正态抽样等知识点的例题，曾作为某年全国的考研题。该题设计巧妙，能够从不同的角度，且只需应用初级的方法就能得出不同的解题思路和解法。

2 基础知识

授课知识点：设X1，X2，……Xn；Y1，Y2，……Yn独立同分布，则

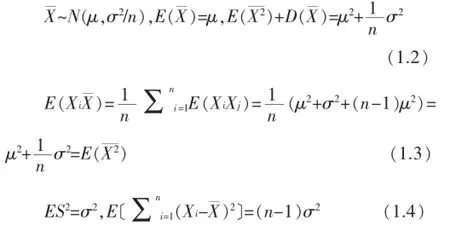
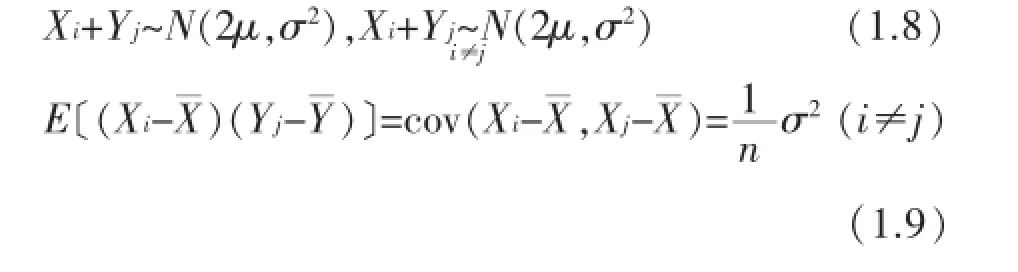
3 常见错误及能力层次分析

3.1 独立性错误

学生在理解统计量与样本关系的时候存在一定的误区，误认为 X1，X2，i=1，2，…，2n，之间是相互独立。比如出现如下的计算过程：

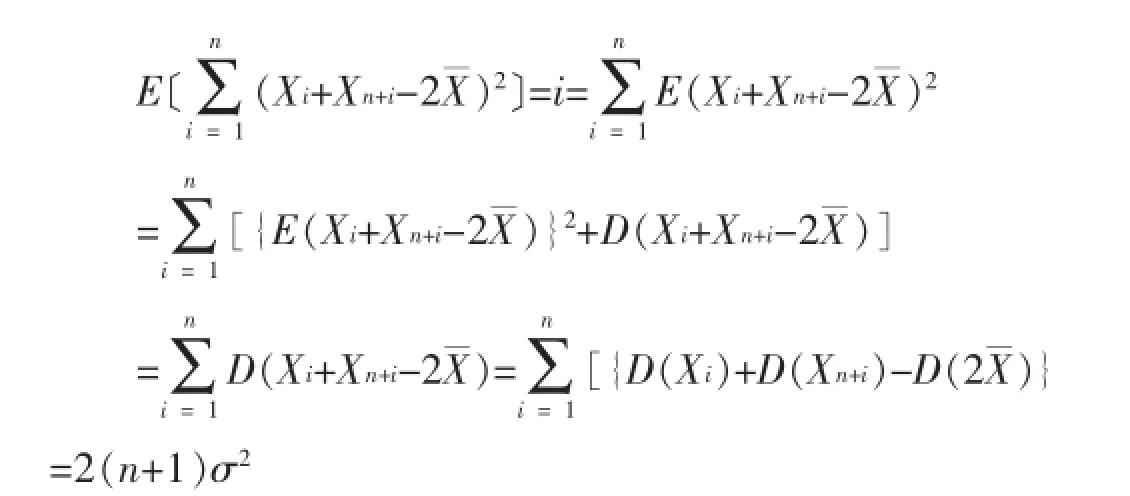
3.2 等价错误

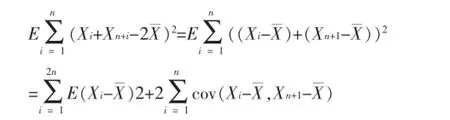
不妨将产生上述错误的学生的能力层次定位为理解偏差型。在教学中，应对该类型的学生加以概念强化，解决其认识上的误区，使其尽快跟上整体教学进度。

4 正确解法评析及能力层次分析

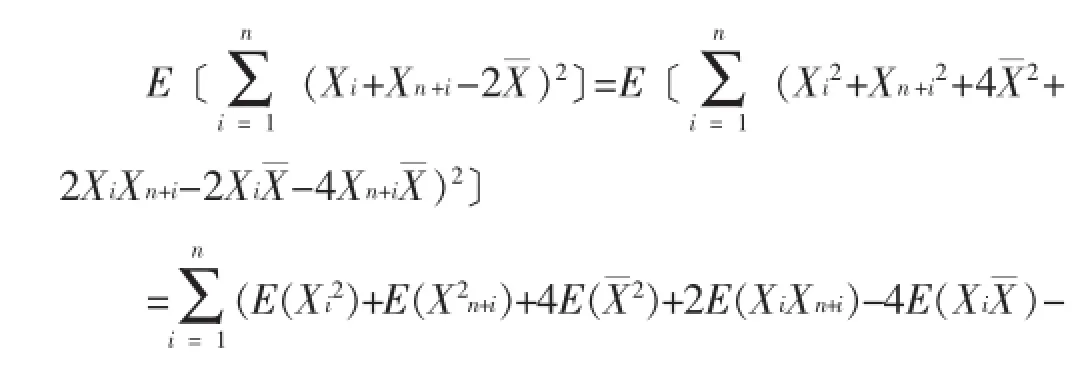
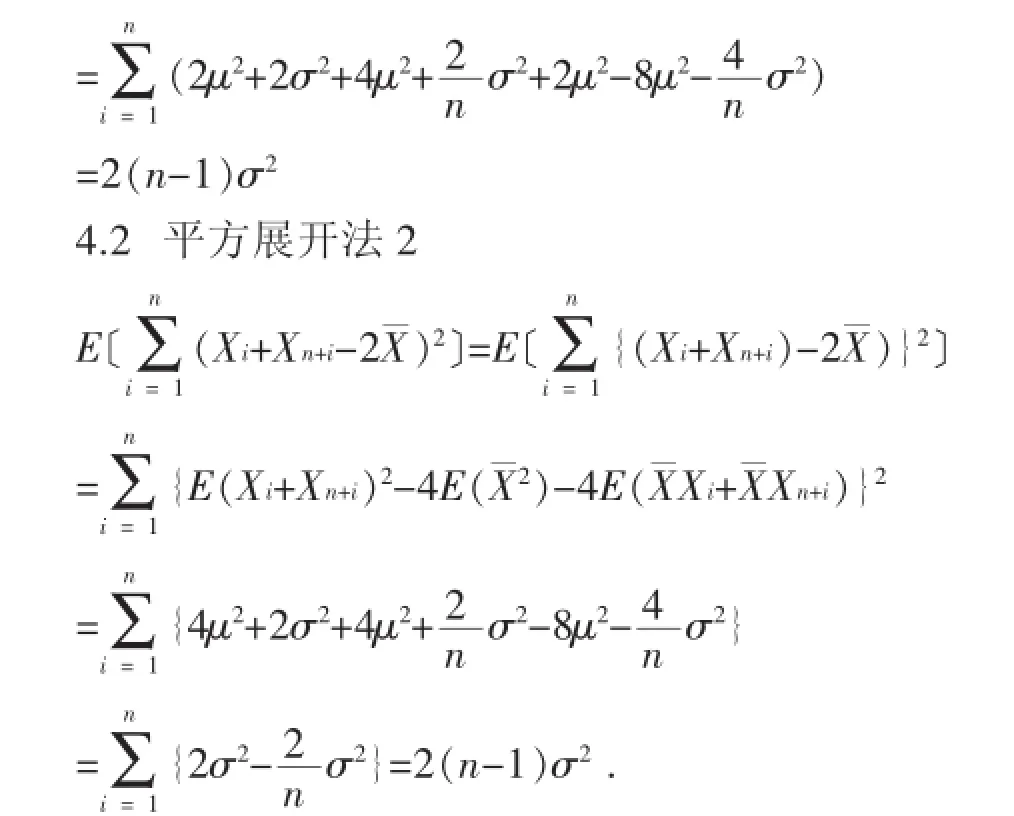
此法是数学学习中最基本的一种方法。因此从知识掌握和能力层次来说，使用该方法的学生，懂得样本、独立同分布的基本概念和基本性质，能熟练使用（1.1）到（1.3）式，具有一定的计算和推导能力。但总体上还处于套用公式的初级阶段，其融会贯通和综合应用能力还有待大力提升，属于基本型I。

4.3 均值分配法

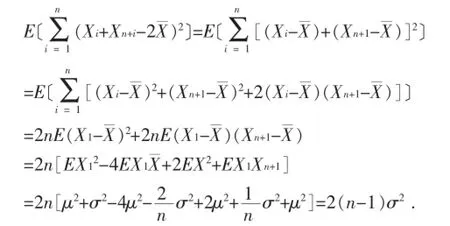
均值分配法实际上是方法3.1的变形，想从2X处入手寻找一种求解的捷径。利用了独立同分布特性，得到以及，在一定程度上简化了求解过程。因此使用该方法的学生对独立同分布的理解基本到位，有一定的应用能力，但还有待提升，属于基本型II。

4.4 公式套用法

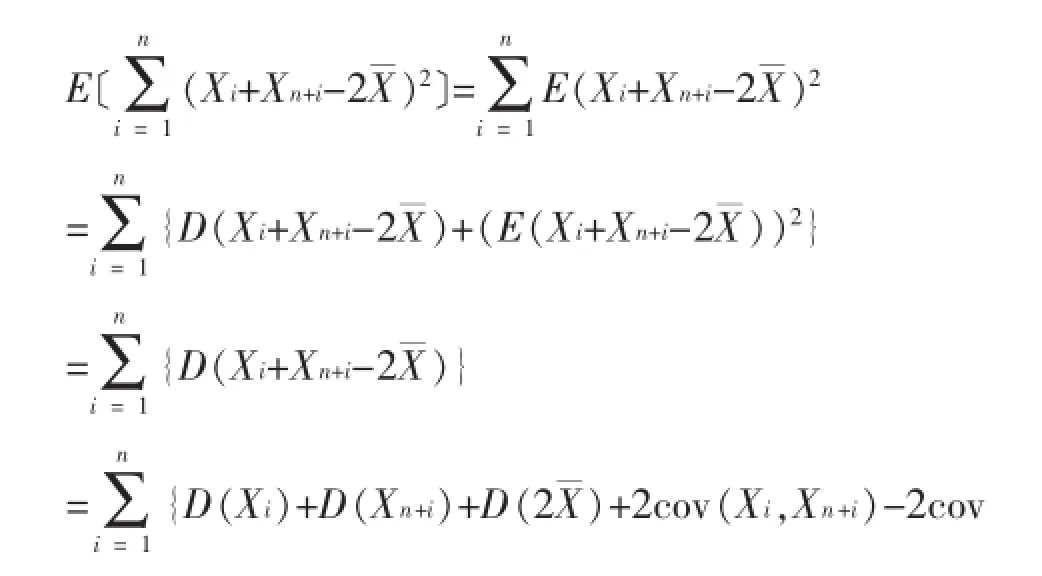
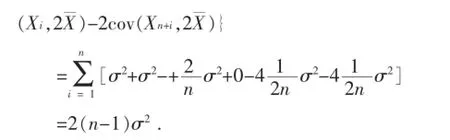
此法实际上应用了（1.1）式和协方差的计算，在一定程度上简化了求解过程。因此使用该方法的学生对独立同分布的理解到位，熟悉方差计算公式，且有一定的应用能力，但还有待提升，属于基本型II。

4.5 均值分配转化

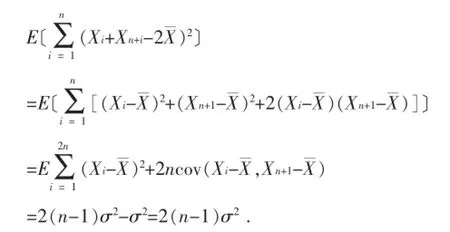
该方法先利用均值分配展开，再转化成样本方差和协方差形式，利用（1.4）和（1.9）式快速得出结果。说明使用该方法的学生对样本方差的期望及协方差的性质及计算非常熟练，基本功扎实，综合应用的能力也很强，这类学生可跨入理解应用型，但还有提高的空间。

4.6 均值分解法

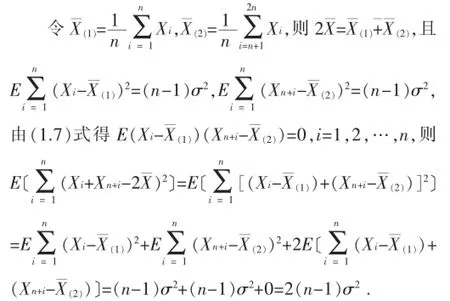
4.7 分布法

此法利用了独立正态随机变量序列的可加性，求得每个子项所服从的正态分布，然后利用期望线性可加的特性求得结果。能够作出这样的推导说明学生对于正态独立可加性以及期望和方差的计算公式领会比较到位，数学逻辑推导能力较强，这类学生可归入理解应用型。

4.8 巧用正态性质法

生态敏感度指生态系统对区域内自然和人类活动干扰的敏感程度，反映区域生态系统遭到干扰时发生生态环境问题的难易程度和可能性，并用以表征外界干扰可能造成的后果。研究区域可大致分为三种类型地形地貌：北部临城区域、西侧临秋浦河区域和东侧接白洋河（清溪河）区域，地势较为平坦；中南部近陀弥山与茱萸山区域地势较高，形成丘陵、山地相间格局；天生湖和谷谭圩区域为山间盆地，湖光山色掩映，风景优美。选取地形地貌、水文、土地类型等作为生态敏感因子进行评分和加权叠加，根据定量评价结果划分低敏感区、较低敏感区、中敏感区、较高敏感区、高敏感区，得到研究区域生态敏感度空间分布（图3、表1）。

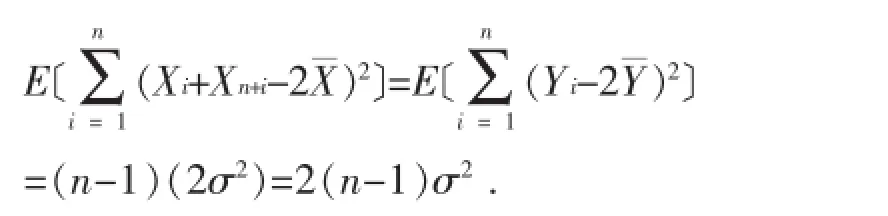
当然，由上述假设，结合正态抽样定理及卡方分布的期望等于自由度的性质，易得

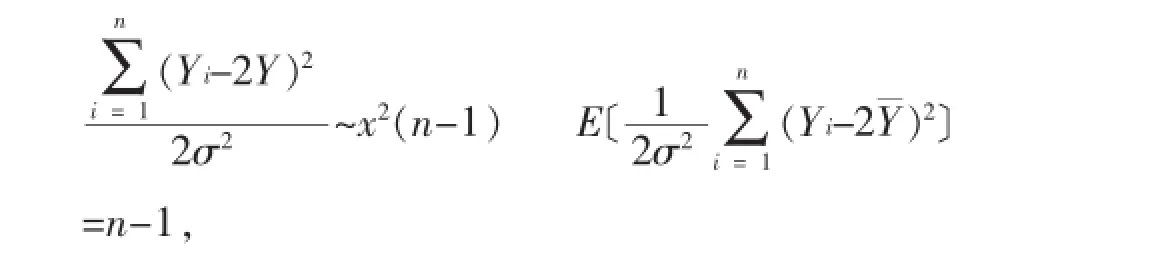
上述这两个解法本质上是一致，均利用了样本方差是总体方差的无偏估计。相对于法3.6而言，法3.7的两种形式就更为简洁巧妙了。能够想到该方法的学生足以说明其充分掌握了正态总体抽样的各种性质和及其抽样定理，并能非常熟练地加以变形、构造和应用。这类学生学习能力很强，数学推证技巧娴熟,且透着一股追求完美的数学情怀，应属于融会贯通型。

5 总结与建议

学生在学习中会存在比较明显的能力和效率差异，这就要求教学模式也要适应这种差异，以学生为核心进行合理的分层教学和因材施教是现代教育发展的必然趋势。文献［2，3］详细探讨了分层教学的诸多问题，我们认为实施分层教学的关键在于适时地监测并掌握学生的能力层次分布。多年的教学实践表明通过作业反馈的方式来获取学生学习效果的第一手信息，是非常有价值的，但不一定是高效的，原因在于作业反馈相对于教学而言是滞后的。但是基于长期的作业跟踪和信息反馈，还是能够比较准确地把握学生掌握课程内容的情况，为及时调整教学模式提供数据依据，以便实施动态的分层教学。

除了及时跟进作业的反馈外，对于作业难易度、综合性等，也是需要刻意把握的，我们认为比较有效的形式包括：

（1）在学习某章内容时，所布置的作业应尽量综合考查到该章的大部分知识点，并有意识地加入能反映能力层次的部分，做好学生作业情况的反馈登记；

（2）在学习了多章内容后，尽量布置综合多章内容的作业，意在训练学生融会贯通的能力和综合应用水平，同样要做好学生作业情况的反馈登记；

（3）通过设计和构建网络测试平台，建设课程的标准题库并植入手机App，将每章的知识点设计成标准题，并将其作为作业的一部分，直接在网上限时完成。这样做的目的是教师可通过测试结果，建立统计分析模型，动态地把握学生整体和个体的学习程度，以便及时作出教学上应对策略。

（4）构建基于App的网络答疑平台，以最便捷的模式建立起教师和学生之间的沟通桥梁，突破时间和空间的限制，实现答疑解惑的高效性。

上述（1）（2）项工作是教学的常规动作，主要依靠任课教师完成；（3）（4）两项工作已列入2015年的校级教学改革项目，目前处在内部测试阶段。

通过作业和测试平台的反馈信息实施动态调整是教学的一种尝试，需要整个基础课教学团队的协同合作，也是一个系统工程。作业和测试平台的反馈还有很多附加作用，其价值包括但不限于以下三个方面：首先解决平时成绩的合理评价问题；其次便于课程负责人客观地掌握全校学生的学习情况和能力层次分布，以便在期末统考命题出卷中做到客观，避免出现严重的偏态现象；便于来年制定更加合理的授课计划和授课进度，为教学的顺利开展提供重要的数据分析支撑。

［1］刘德金.从“求圆截线平面问题”的研究谈学生能力的培养［J］.大学数学，2011（6）.

［2］刘龙，李明，于滨，等.关于高等数学课分层次教学的思考［J］.教育探索，2008（11）.

［3］张香云，王家军，贺志民.高等数学课程分层次教学理念的思考和举措［J］.大学数学，2014（1）.

［4］陈思源.利用对称性巧解概率与数学期望问题［J］.高等数学研究，2007（4）.

［5］尹长明，韦程东.公共基础课“概率论与数理统计”教学的一点体会［J］.广西大学学报（自然科学版），2008（S1）.

［6］焦万堂，李俊海，曹建莉.科学思维、科学方法在概率论与数理统计教学中的应用研究［J］.大学数学，2013（1）.

G642，O212

：A

：1673-9884（2017）01-0083-04

2016-09-20

福建省本科高校教育教学改革研究项目（JAS151395）；福州大学研究生课程建设项目（52004634，52004612）

吕书龙，男，福州大学副教授，硕士。