智能分析方法及其在岩土工程中的应用
2017-04-11钱劲斗柯晓峰何章津
郭 健,殷 俊,李 婷,钱劲斗,柯晓峰,何章津
(武汉轻工大学 土木工程与建筑学院,湖北 武汉 430023)
智能分析方法及其在岩土工程中的应用
郭 健,殷 俊,李 婷,钱劲斗,柯晓峰,何章津
(武汉轻工大学 土木工程与建筑学院,湖北 武汉 430023)
随着计算机技术的迅速发展,以复杂问题为研究对象的智能学科出现,为解决复杂系统提供了一种全新的研究途径。系统地评述了智能算法研究现状,回顾了智能分析方法在岩土工程中的应用。面对复杂施工条件和外部环境,岩土工程极具随机性、不确定性、模糊性特点,制约着地下工程破坏机理的准确分析和安全风险的精确预测,如何提高岩土工程施工安全可靠性、防控施工风险、减少工程事故的发生,已成为亟待解决的问题。展望岩土工程智能研究及应用前景,运用数据融合技术,研发具有智能分析特点的岩土工程集成专家系统,用以实现施工信息化,满足岩土工程风险实时预测及控制的要求,将是未来岩土工程智能研究发展的方向。
智能分析;复杂系统;岩土工程;施工信息化;预测控制
1 引言
近十年以来,随着我国经济的快速发展和国家中心城市战略的实施,大体量、超大体量的建(构)筑物层出不穷,与岩土工程相关的大型工程项目正以前所未有的速度进行,大量城市交通设施如地铁隧道建设,在建的城市地下空间、深大基坑工程等,其建设规模与难度越来越大[1-3],如何实现岩土工程施工的安全可靠要求,对工程科研、设计及施工提出了严峻的挑战。
岩土工程是以岩土材料的物理力学性质、岩土力学的基本理论及岩土工程设计施工的理论与方法为研究对象,通过分析岩土体工程力学性质并将其应用于工程的学科。由于天然岩土体所赋存的地质环境特殊,受多场(应力场、温度场、渗流场)、多相(气相、液相、固相)等复杂因素的影响,表现出高度非线性、非均质、非连续性及多相性的复杂耦合特点[2]。面对高维、强耦合、时变性和随机性的岩土工程,复杂条件下的岩体变形破坏机制难以准确地理解,致使经典的岩土力学分析很难给出精确的模型和参数问题[3]。因此,如何准确地确定其力学参数和本构模型,一直是岩土工程界亟待解决的主要问题[4]。
2 岩土工程数值分析方法的研究
国内外众多学者经过几十年的不断研究探索与工程实践,岩土工程数值分析方法由经验、半经验向计算复杂、高精度的方向发展。
经典的岩土工程问题分析求解方法根据固体力学原理,基于假定确定性,通过数值分析求解的经典力学问题,即根据岩土体物理参数、本构模型及边界条件,按照弹塑性力学计算岩土体中的应力、应变及位移等[5]。由于岩土工程的处理对象为性质极其复杂的天然岩土体,其自身介质材料性质具有模糊性、不确定性、随机性,其物性参数及本构模型不易得到, 其计算边界条件难以确定,难以进行确定性的正分析,为此非确定性的反分析方法应运而生[6-7]。
反分析方法是将反演分析获取的参数,作为同一模型下正分析的输入参数,用以提高结构分析的可靠性。其研究涉及:模型与参数辨识、参数灵敏度分析、求解稳定性和局部极值点,其中,参数和模型的正确抉择是岩土工程研究中的两大难题[8]。
在20世纪70年代,两位学者Karanagh和Clough首先提出反演弹性固体的弹性模量有限元分析方法[9],用于指导岩土工程设计和施工,这是岩土工程领域出现的一种新的计算方法——反分析方法(Back Analysis)的出现。
岩土工程的反分析方法是基于岩土工程问题的一些先验信息,以现场量测的、反映系统力学行为的物理信息(如位移、应变、应力或荷载等)和围岩介质的特性与参数,采用处理非确定性问题的相应方法,通过反演模型(系统的物理性质模型及数学描述)推算得到该系统的各项或某些初始参数(如初始应力、本构模型参数、支护荷载、边界荷载等)[10-12],获取岩土工程系统的分析模型,为数值分析提供“计算参数”,使之用于工程监控、预测和安全评价。它是逆向思维的一次成功应用,即以量测监控技术和现代控制技术为基础,发展现场监控量测信息的反分析方法[13-14],开辟了岩土参数和初始地应力研究的新途径,因而对岩石力学与工程学科理论发展具有划时代的意义。
岩土工程“逆问题”是相对“正问题”而言的,是根据现场实测值反求岩土体物理力学性质参数或其本构模型的一种手段,它不单纯是一种力学的求解过程,包含了系统控制及优化技术方法。
岩土工程反分析方法经过多年的发展,已由线性发展到非线性,目标未知数由单纯的计算参数发展到岩土体的本构模型,材料由均质发展到非均质,在确定性反分析的基础上又发展了非确定性反分析,使得岩土工程反分析的计算理论日趋成熟。由于反分析法在解决复杂岩土工程问题上的准确性和可靠性,而备受岩土工程界的重视,并被用于预测分析领域,取得了令人瞩目的研究成果。
国内外众多学者,Gioda[15]、Sakurai[16]、樱井春浦[17]等,在解决岩土工程中材料的非均质性、非线性和不连续性造成的本构模型及力学参数等问题,取得显著的科研成效;孙钧院士[18]、冯夏庭[4-5]、杨志法[19]、杨林德[19]、王芝银[20]、吕爱钟[21]和傅鹤林[22]等人,通过研究解的唯一性、稳定性和参数敏感性等,提出了多种反分析方法,形成了一套完整的“现场监测—反演分析—工程检验—分析预测”分析系统,成功地应用于岩土工程领域,获取了力学参数,并对岩土工程进行了合理评价与有效预测。
3 智能岩土分析方法研究
3.1 智能算法研究
智能的思想源于复杂适应系统理论以及人工生命的研究[23-24]。自然界的自适应优化现象不断给计算机科学家们以灵感,使他们通过模仿自然世界的内在机制获取解决复杂计算问题的新方法。
自20世纪90年代以来,一些学者受到自然界生物群体“鸟类聚集飞行行为、蚂蚁觅食行为、鱼群行为”等所表现出的自组织行为和群体智能现象的启发,诞生了以粒子群算法和蚁群算法等为代表的模拟生物群体行为的“群体智能”算法[25],极大地丰富了智能优化技术,并被公认为是继人工智能之后,2l世纪计算技术中最有影响的关键技术。美国学者Kennedy和Eberhart博士于2001年出版的《Swarm Intelligence》[26]成为群体智能研究与发展中的一个重要历程碑。
智能技术经过多年的发展逐步形成了三个层次[27-28]:第一层生物智能,主要研究智能的产生、形成和工作机理;第二层人工智能,主要研究应用符号逻辑方法模拟人思考问题,具有求解、推理、学习等方面的能力,偏重于逻辑推理;第三层计算智能又称为智能算法,主要是通过模拟人、自然及生物种群的结构特点、进化规律、行为方式及思维结构而发展起来的,基于数值计算和结构演化的智能方法偏重于数值计算,主要用来实现智能的研究与应用。
近年来不同类型智能算法开始走向融合,形成具有复合协同的可模拟生物行为的智能混合算法,这类智能混合技术在求解一些用传统方法难以得到满意解的复杂困难问题时具有明显的优势,为摆脱传统人工智能所面临的困境提供的一种新的方向。
3.2 智能仿生算法在岩土工程中的应用研究
随着智能技术和计算机学科的迅猛发展,计算分析能力的提高,大规模并行处理技术的产生,以不确定性、非线性、时间不可逆性为内涵,以复杂问题为对象的新兴边缘交叉学科的出现[29-31],新的理论(优化理论、灰色理论、突变理论、分形几何理论、混沌理论、可靠度理论、随机过程理论等)具有随机搜索性能的人工智能分析方法逐渐发展起来,都为具有时变特点的岩土工程问题解决提供了一种全新研究途径。
岩土工程界深入研究并运用模糊计算、神经网络、蚁群算法、粒子群算法、遗传算法等智能算法,在隧道、岩坡、坝基和基坑等工程领域取得了十分显著科研成果。
在国外,Brown等[32]将前馈神经网络应用于复合材料本构模型的识别。Theocaris[33]将神经网络应用于塑性硬化本构模型识别。Tomonari[34]将粘弹塑性本构方程表达为一阶微分方程,提出了一种神经网络本构模型。Ghaboussi等[35]利用自学习与自适应算法直接从工程实测位移中提取所需的学习样本。Daoheng[36]将神经网络应用于弹塑性本构模型的识别。
在国内,20世纪90年代,孙道恒等[37]提出了力学反问题的神经网络分析方法。李立新等[38]利用BP网络模型,以岩体的粘弹性位移反分析为基础,反演得到岩体粘弹性力学参数。张清[39]将人工神经网络引入岩石力学中。李端有等[40]提出了基于人工神经网络的边坡位移反分析方法,取得了三峡永久船闸开挖边坡多介质岩体的宏观等效弹性模量,并利用各层等效模量进行了有限元正分析计算,预测三峡永久船闸开挖边坡下一开挖阶段的应力及变形发展趋势。樊琨等[41]基于人工神经网络,建立了非线性力学反分析模型,求得了岩土工程计算中邓肯参数。杨成祥[42]用神经网络进行模型识别的关键是获取学习样本。冯夏庭等[43-44]提出了进化神经网络反分析思想,按正交设计方法获得样本进行学习,用遗传算法搜索最佳网络结构,用最佳推广预测学习算法训练网络,建立了岩土体力学参数与位移的非线性关系,并进行岩体力学参数最优辩识。
进入21世纪,2000年葛增杰等[45]提出了深基坑开挖工程多层土体物性参数识别的BP算法,求得了各层土体的弹性模量。高玮等[46]采用快速遗传算法进行岩土工程反分析,求得了包括弹性模量、粘塑性参数在内的7个物性参数。
2001年,谭云亮等[47]利用径向基函数神经网络快速提取岩石的本构模型,根据实测位移,采用位移反分析方法获得学习样本。周瑞忠等[48]以模拟深基坑开挖的有限元程序为正演工具,以BP网络为反演工具,将正演过程与反演过程结合起来,根据反演结果指导下一步施工,形成一个良性循环。李晓红等[49]运用BP网络模型对岩体力学参数、工程结构参数及位移量测资料的学习,得到了隧道围岩稳定性分析所需要的三个重要参数(等效弹性模量E、初始地应力侧压力系数入和铅垂地应力σ)。高玮等[50]提出了岩土力学反分析的集成智能思想,综合运用专家系统的推理、决策能力,数值计算的定量分析能力及人工神经网络的直觉思维能力,进行位移反分析。
2002年,蒋中明等[51]结合有限变形理论和人工神经网络理论,反分析初始地应力场。
2004年,赵洪波等[52]运用遗传算法来搜索支持向量机的参数和核函数,描述变形时间序列之间的映射关系,解决了位移反分析的计算问题。姜谙男等[53]综合应用遗传算法和神经网络,建立了进化神经网络演化有限元差分方法,该方法解决了大规模的锚固参数定量优化问题。
2005年,张福波等[54]采用神经网络理论对基坑坑壁位移进行了模拟预测,为深基坑工程施工风险控制提供了新的思路。
2006年,吴余生等[55]将自适应有限元法与改进的遗传算法与模拟退火算法相结合,能以较快的速度搜索到边坡临界滑动面。高玮[56]将粒子群优化算法与有限元数值分析技术进行融合,用于隧道位移反分析,提高了反分析的计算性能。许传华等[57]利用模拟退火算法对地下洞室岩体的力学参数进行位移反分析,提高了反演的效率精度。
2007年,冯夏庭[4]等运用岩石力学模型和参数综合智能反分析方法,解决了待反演参数的敏感性、反演的参数个数以及模型参数反演结果的适应性评价等问题。余志雄等[58]提出了一种基于改进支持向量机和改进遗传算法的随机反分析方法,用于初始地应力场位移分析,具有较高的拟合精度和预测效果。姜谙男[59]利用粒子群优化支持向量机参数,建立变形时间序列模型,用于清江水电站地下厂房围岩变形预测,获得令人满意的预测精度。
2008年,郭健[60]、梁桂兰[61]等提出了粒子群优化径向基函数神经网络的随机优化算法,用于岩土工程应力、位移非线性时间序列的预测预报,具有较高的收敛速度和预测精度。
2011年,黄戡等[62]基于正交试验设计和FLAC建立的测试样本,用遗传算法-神经网络,建立待反演参数与围岩位移之间潜在的映射关系实现位移反分析,成功将反演结果应用于隧道的信息化施工。
2014年,李珉等[63]采用遗传进化算法与数值分析方法,建立岩石参数的智能等效模型,反演煤矿井下岩土参数,分析结果与实测结果高度吻合。
2016年,马春景[64]等运用差异进化算法,成功地对渗流稳定后围岩流量变化渗透系数进行了反演。
4 岩土工程智能预测控制系统研究
4.1 基于非线性系统智能辨识与预测
非线性系统辨识过程中,将时变对象看做一个“黑箱”,采用智能算法建模,利用非线性网络的映射能力,通过内部隐含在输入输出数据特性完成时变系统的辨识。该方法可成功地避开传统意义的、确定数学关系的模型,具有概念简单、实用方便的特点。
岩土工程反分析目的不仅是为了确定工程范围内岩体初始地应力的计算参数、辨识力学特性参数,更重要的是将现场监控技术与工程稳定性分析相结合,对不同工况条件下评价工程的可靠性并做出符合实际的预测,根据动态模型对系统未来行为进行预测和优化的控制策略,用于解决具有不确定性的时变系统问题,对施工进行有效风险控制。
针对岩土工程中日益突出的非线性问题,基于线性SISO与非线性MIMO系统,存在着难以对时变系统进行有效地辨识的问题,已无法满足岩土工程风险预测及控制要求。而智能算法在非线性MIMO系统的数学建模与控制方面,具有经验类比、回归分析等传统方分析法无法比拟的优势,并已逐步成为实现非线性预测控制的关键技术。非线性系统的辨识与预测智能化已成为当前岩土工程界的研究热点之一。
国内外的众多学者一直致力于非线性MIMO控制系统智能化的研究,并已在预测控制智能化方面取得众多的研究成果。1992年Su等将递归神经网络用于化工工程多步预测[65];Buescher等提出一种非线性预测控制时间二尺度方案,利用神经网络建立了预测模型[66];Najim等采用多输入多输出的前馈神经网络控制网络,利用递归神经网络进行了多步预测[67];刘晓华等提出了对模型误差具有动态补偿能力的预测控制算法[68];丁烈云院士[1]、郭健[2]与周诚[3]构建具有智能分析处理技术的隧道工程安全预警系统,成功地用于武汉长江隧道盾构施工风险分析。
4.2 岩土工程反分析系统
从系统角度来看,岩土工程研究对象为复杂的巨系统,其岩土体的初始应力、力学参数可看成系统输入,量测信息(位移、变形破坏等)均可看成系统对输入的反应的输出。由于施工中的位移、应力、应变等均可观测得到,求解的结果为系统模型、状态参数等,即反分析过程实质上是一个系统辨识问题[50]。而岩土工程反分析系统可由一个灰色系统的输出到输入的映射过程进行描述(如图1所示),则可根据现场的实测位移、应力、应变等,可为岩土工程提供与实际相吻合的岩土体力学参数、地层初始地应力以及边界荷载等。
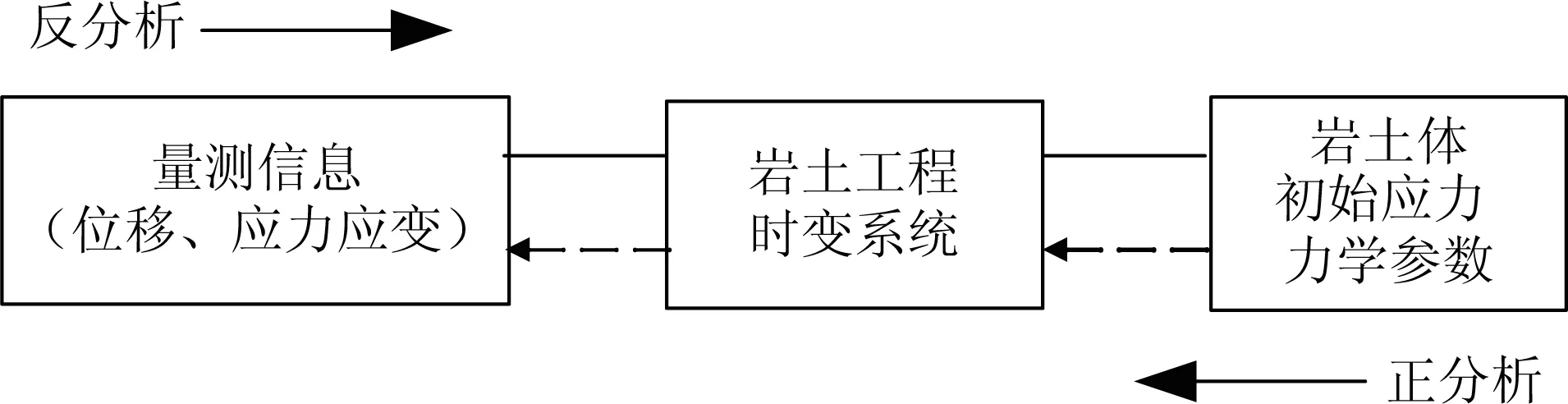
图1 岩土工程的反分析系统
由于岩土体所处的力学状态不同,采用本构关系不同,反分析得到的力学特性参数也是不同[69]。工程现场采集的岩土体量测参数,含有丰富的参量信息,是岩土体力学性质及各种因素的综合反映,其参量可描述为:
u=f(σ,τ,μ,E,c,φ,η,t).
(1)
式中 :σ、τ为地应力分量,μ、E分别为岩体的泊松比、弹性模量,c、φ分别岩体的内聚力、内摩擦角,η、t分别岩体的粘滞系数、时间。
由于位移反分析法是以位移量测信息为基础,需对岩土体的力学模型及相应的边界条件选择,建立合适的目标函数,故可采用智能技术来反推待求的参数,其目标函数可描述为:
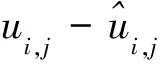
(2)
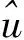
根据反分析原理,岩土反分析过程实际上是一个目标函数的优化过程,即根据现场量测信息,结合数值分析方法,将初始应力和岩体参数作为待求未知量,建立目标函数关系式,通过不断优化寻找目标函数最小值进行求解,则该问题可描述为:

(3)
如果用F表示可行解区域,那么F中的任何一个元素为优化问题可行解,则有:
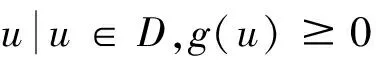
(4)
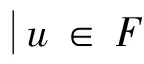
4.3 岩土工程预测控制系统
智能预测控制是借鉴智能仿生原理,利用智能算法(IA)建立的系统辨识模型,实现非线性系统预测控制。其系统结构是基于两个模型,一个是预测模型,主要通过动态建模,以获取预测信号;另一个是控制模型,主要根据预测目标函数得到的相应驱动信号,以获得预测控制律函数,其描述为:
y(k)=f[Yk,Uk,Dk]T.
(5)
式中,f(·)为非线性函数;Yk和Uk分别为网络在k时刻的输出和输入向量;Dk为随机噪声向量。
岩土工程时变系统的预测,是通过性能指标J(k)的优化来实现对未来行为进行控制,其性能指标可描述为:
minJ(k)=min∑Nk=1(y(k)-yp(k))2.
(6)
式中,N为观测样本数。
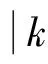
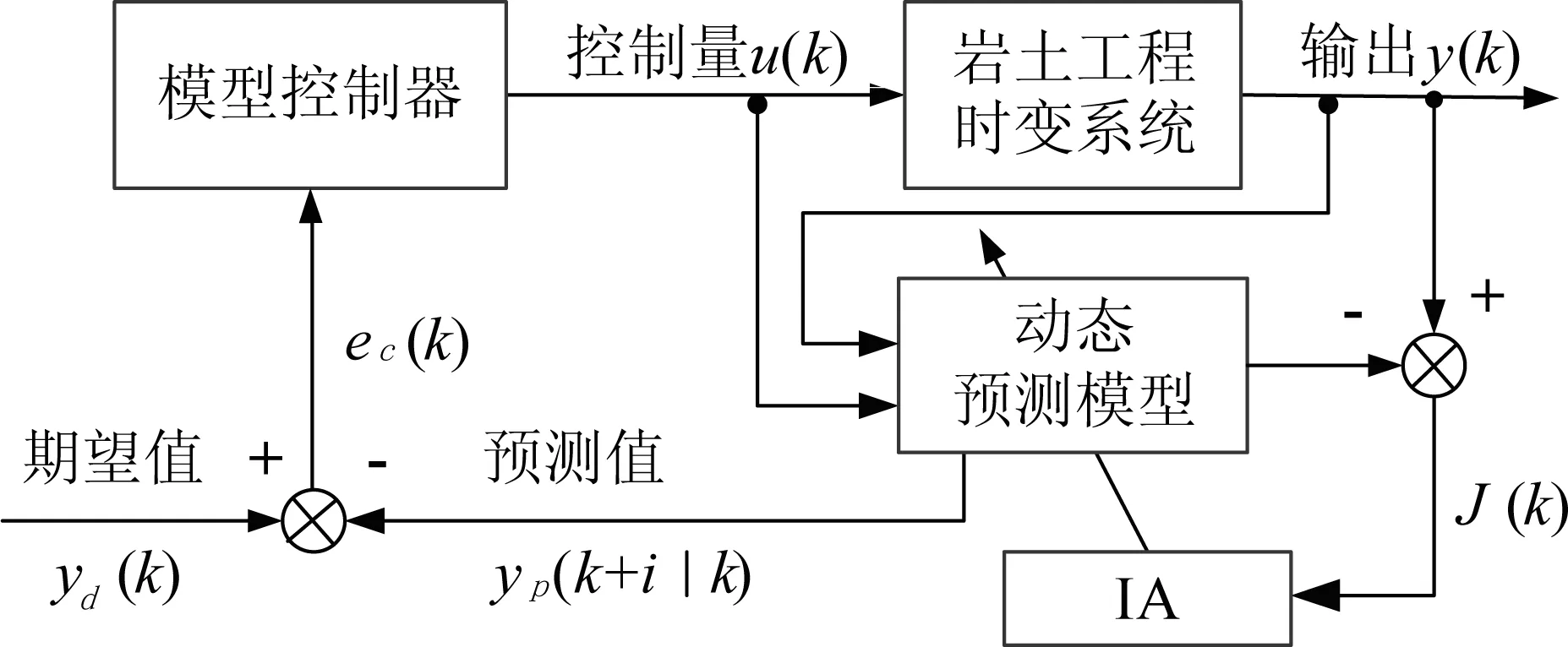
图2 岩土工程时变系统智能预测控制原理图
岩土工程的预测控制系统,可描述为[70]:
x(k+1)=f(x(k),u(k),k).
y(k)=g(x(k),k).
(7)
式中,k=0,1,2……表示当前时刻,x(k)∈Rn为系统k时刻的状态向量,u(k)∈Rr为控制输入向量,y(k)∈Rm输出向量。
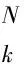
x(k+i|k)=f(x(k+i-1|k),u(k+i-1)).
yp(k+i|k)=g(x(k+i-1|k)).
(8)
式中,i=0,1,……,np,np为控制时域。则有,
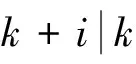
(9)
由此可实现岩土工程系统预测的目的。
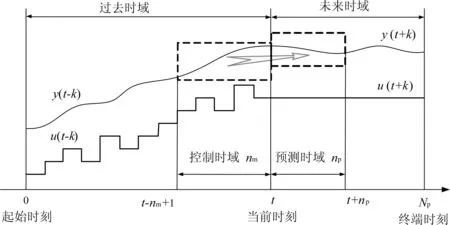
图3 岩土工程时变系统滚动预测控制过程
5 结论
随着计算机智能技术的迅速发展,大规模并行处理技术的产生和理论的成熟,以不确定性、非线性、时间不可逆性为内涵,以复杂问题为对象的新兴智能交叉学科的出现,为解决大规模、复杂系统工程,提供一种全新的研究思路。
笔者以复杂系统为对象,总结和回顾了智能分析方法的研究与现状,以及研究岩土工程超复杂系统智能化的意义。
面对复杂施工环境和外部环境的影响,大型岩土工程通过引入现代智能分析方法,将智能分析与虚拟技术进行融合,研发具有大数据信息融合技术的智能分析及风险预测控制系统,解决岩土工程中大量的非线性、时变问题,满足快速分析、实时预测控制要求,实现“设计-施工”信息化,具有很高的工程应用前景。
[1]DingLY,WangF,LuoHB,etal.Feed-forwardanalysisforshield-groundsystem[J].ASCEJournalofComputinginCivilEngineering. 2013, 27(3):231-242.
[2]JianGuo,LieyunDing,HanbinLuo,etal.WaveletPredictionMethodforGroundDeformationInducedbyTunneling[J]..TunnelingandUndergroundSpaceTechnology, 2014, 41 (3): 137-151.
[3]ZhouC,DingLY,HeR.PSO-basedElmanneuralnetworkmodelforpredictivecontrolofairchamberpressureinslurryshieldtunnelingunderYangtzeRiver[J].AutomationinConstruction. 2013, 36: 208-217.
[4] 冯夏庭,周辉,李邵军,等.岩石力学与工程综合集成智能反馈分析方法及应用[J].岩石力学与工程学报.2007, 26(9):1737-1744.
[5] 冯夏庭. 智能岩石力学导论[M]. 北京: 科学出版社, 2000.
[6] 孙钧, 蒋树屏, 袁勇,等. 岩土力学反演问题的随机理论与方法[M]. 汕头: 汕头大学出版社, 1996.
[7] 高玮,郑颖人. 岩土工程非确定性反分析研究动态[J]. 地下空间.2000, 20(2):81-85.
[8] 孙钧. 岩土力学与地下工程结构分析计算的若干进展.力学季刊[J].2005, 26(3):329-338.
[9]KavanaghKT,CloughRW.Finiteelementapplicationinthecharacterizationofelasticsolids[J].InternationalJournalofSolidsStructures, 1971, 7(1): 11-13.
[10]AraiK,OhtaH,YasuiT.Simpleoptimizationtechniqueforevaluationdeformationmodulifromfieldobservations[J].SoilandFoundations, 1983, 23(1): 107-113.
[11]YangL,SterlingRL.Backanalysisofrocktunnelusingboundaryelementmethod.JournalofGeotechnicsEngineering[J], 1989,115(8): 1163-1169.
[12]HonjoY,LiuWT,SakajoS.ApplicationofAkaikeinformationcriterionstatisticstogeotechnicalinverseanalysis:theBayesianmethod[J].StructuralSafety, 1994, 14(11): 5-29.
[13]KavanaghKT,CloughRW.Finiteelementapplicationinthecharacterizationofelasticsolids[J].InternationalJournalofSolidsStructures, 1971, 7(1): 11-13.
[14]GiodaG,MaierG.Directsearchsolutionofaninverseprobleminelastic-plastic:identificationofcohesion,frictionangleandin-situstressbypressuretunneltests[J].InternationalJournalforNumericalMethodsinEngineering, 1980, 15(11): 1823-1848.
[15]GiodaG,PandolfiA,CividiniA.Acomparativeevaluationofsomebackanalysisalgorithmsandtheirapplicationtoin-situloadtests[J].Proceedingsof2ndInternationalSymposiumonFieldMeasurementinGeom.Kobe, 1987, 1131-1144.
[16]SakuraiS,TakeuchiK.Backanalysisofmeasureddisplacementoftunnel[J].RockMechanicsandRockEngineering, 1983, 16(3): 173-180.
[17] 樱井春辅. 地下洞室设计和监控的一种途径[J]. 隧道译丛, 1986, 4: 13-25杨林德. 岩土工程问题的反演理论与工程实践. 北京: 科学出版社, 1996.
[18] 杨志法, 王思敬, 冯紫良,等. 岩土工程反分析原理及应用[M]. 北京: 地震出版社, 2002.
[19] 杨林德, 黄伟, 王聿. 初始地应力位移反分析计算的有限单元法. 同济大学学报, 1985, 13(4): 370-373.
[20] 王芝银, 杨志法, 王思敬. 岩石力学位移反演分析回顾及进展[J]. 力学进展, 1998, 28(4): 488-498.
[21] 吕爱钟, 蒋斌松. 岩石力学反问题[M]. 北京: 煤炭工业出版社, 1998.
[22] 傅鹤林, 彭思甜, 韩汝才等. 岩土工程数值分析新方法[M]. 长沙: 中南大学出版社, 2005.
[23] 米歇尔·沃尔德罗. 复杂-诞生于秩序与混沌边缘的科学[M]. 北京: 三联书店, 1997.
[24] 许国志, 顾基发, 车宏安. 系统科学.上海: 上海科技教育出版社, 2000.
[25]KennedyJ,EberhartRC.Particleswarmoptimization[C].In:Proc.IEEEInternationalConferenceonNeuralNetworks.Piscataway,NJ:IEEEServiceCenter, 1995, 1942-1948.
[26]KennedyJ,EberhartRC.SwarmIntelligence[M].SanFrancisco:MorganKaufmannPublishers, 2001.
[27]LangtonCG.ArtificialLife.VolumeVIofSFIStudiesofComplexity[M].AddisonWesley, 1989.
[28]Fhat-Torbraghan,Madjid.HildebrandLars.ComplexSystemAnalysisUsingCl-mehtods[C].ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering, 1999, 300-341.
[29] 戴汝为. 科学的前沿与未来[M]. 北京: 科学出版社, 1998.
[30]WaldropMM.Complexity:TheEmergingScienceattheEdgeofOrderandChaos[M].NewYork:TouchstoneBooks, 1993.
[31] 宋学锋. 复杂性、复杂系统与复杂性科学[M]. 中国科学基金, 2003, 17(5): 262-269.
[32]BrownDA.MurthyPLN.Computationalsimulationofcompositeplaymicromechanicsusingartificialneuralnetworks[J].MicrocomputersinCivilEngineering.1991, 6(2): 87-97.
[33]TheoearisPS,PanagiotopoulosPD.Generalizedhardeningplasticityapproximatedviaanisotropicelasticity:aneuralnetworkapproach[J].ComputerMethodsinAppliedMechanicsandEngineering, 1995, 125(2): 123-139.
[34]TomonariDA.Implicitconstitutivemodellingforvisco-plasticityusingneuralnetworks[J].InternationalJournalforNumericalMethodsEngineering, 1998, 43(3): 195-219.
[35]GhaoboussiJ,SidartaDE.Newnestedadaptiveneuralnetworks(NANN)forconstitutivemodeling[J].ComputersandGeotechnics, 1998, 22(1): 29-51.
[36]DaohengS,QiaoH,HaoX.Aneuro-computingmodelfortheelastic-plasticity[J].ComputerMethodsinAppliedMechanicsandEngineering, 2000, 18(2): 177-186.
[37] 孙道恒, 胡俏, 徐灏. 力学反问题的神经网络分析法[J]. 计算结构力学及其应用, 1996, 13(3): 308-312.
[38] 李立新, 王建党, 李造鼎. 神经网络模型在非线性位移反分析中的应用[J]. 岩土力学, 1997, 18(2): 62-64.
[39]ZhangQ,YangY.TheapplicationofneuralnetworktoRockEngineeringSystems(RES) [J].InternationalJournalofRockMechanicsandMiningSciences, 1998, 35(6): 727-745.
[40] 李端有, 李迪, 马水山. 三峡永久船闸开挖边坡岩体力学参数反分析[J]. 长江科学院报, 1998, 15(2): 10-13.
[41] 樊琨, 刘宇敏, 张艳华. 基于人工神经网络的岩土工程参数反分析 [J]. 河海大学学报, 1998, 26(4): 98-102.
[42] 杨成祥. 材料本构模型自适应识别的初步研究[D]. 沈阳: 东北大学, 1998.
[43] 冯夏庭, 习心宏. 智能岩石力学 (1)-导论[J].. 岩石力学与工程学报, 1999, 18(2): 222-226.
[44] 冯夏庭, 杨成祥. 智能岩石力学(2)-参数与模型的智能辨识[J].. 岩石力学与工程学报, 1999, 18(3): 350-353.
[45] 葛增杰, 李锡菱. 深基坑开挖工程多层土体物性参数识别的BP法 [J]. 大连理工大学学报, 2000, 40(3): 271-275.
[46] 高玮, 郑颖人. 采用快速遗传算法进行岩土工程反分析[J]. 岩土工程学报, 2001, 23(1): 120-122.
[47] 谭云亮, 王春秋.岩石本构关系的径向基函数神经网络快速逼近模型[J].岩土工程学报, 2001, 23(1): 14-17.
[48] 周瑞忠, 邱高翔. 基于BP网络的深基坑支护位移反分析[J]. 土木工程学报, 2001, 34(6): 60-62.
[49] 李晓红, 靳小光, 亢会明. 隧道位移智能化反分析及其应用[J]. 地下空间, 2001, 21(4): 299-304.
[50] 高玮, 郑颖人. 岩土力学反分析及其集成智能研究[J]. 岩土力学, 2001, 22(1): 114-116.
[51] 蒋中明, 徐卫亚, 邵建富. 基于人工神经网络的初始场应力三维反分析[J]. 河海大学学报, 2002, 30(3): 52-56.
[52] 赵洪波, 冯夏庭. 非线性位移时间序列预测的进化-支持向量机方法及应用[J]. 岩土工程学报, 2003, 25(4): 468-471.
[53] 姜谙男, 冯夏庭, 刘健,等. 基于三维数值模拟的地下大型洞室锚固参数智能优化[J]. 岩石力学与工程学报, 2004, 23(10): 1700-1705.
[54] 张福波, 陈有亮. 基于BP神经网络与模糊控制的深基坑开挖侧向变形分析[J].. 岩土力学, 2005, 26(7): 1148-1152.
[55] 吴余生, 陈胜宏. 并行组合模拟退火算法在边坡稳定分析中的应用[J]. 岩土力学, 2006, 27(9): 1554-1558.
[56] 高玮. 基于粒子群优化的岩土工程反分析研究[J]. 岩土工程学报, 2006, 27(5): 795-798.
[57] 许传华, 任青文, 郑治,等.索风营水电站地下洞室岩体力学参数的位移反分析[J]. 岩土工程学报, 2006, 28(11): 1981-1985.
[58] 余志雄, 周创兵, 陈益峰,等. 基于V-SVR和GA的初始地应力场位移反分析方法研究[J]. 岩土力学, 2007, 28(1): 151-156.
[59] 姜谙男. 基于PSO-SVM非线性时序模型的隧洞围岩变形预报[J]. 岩土力学, 2007, 28(6): 1176-1180.
[60] 郭健, 王元汉, 苗雨,等. 桩筏(箱)基础沉降多步预测控制的IPSO-Elman算法[J]. 华中科技大学学报(自然科学版). 2008, 36(6): 96-99.
[61] 梁桂兰, 徐卫亚, 何育智,等,PSO-RBFNN模型及其在岩土工程非线性时间序列预测中的应用[J]. 岩土力学, 2008, 29(14): 995-1000.
[62] 黄戡,刘宝琛,彭建国,等.基于遗传算法和神经网络的隧道围岩位移智能反分析 [J]. 中南大学学报(自然科学版).2011,42(11): 213-219.
[63] 李珉, 张敏, 孟杰. 基于数学优化算法的煤矿井下岩体参数识别技术研究[J]. 煤炭技术.2014, 33(02):168-170.
[64] 马春景, 姜谙男, 王军祥,等. 基于差异进化算法的隧道渗流反分析与工程应用[J]. 铁道科学与工程学报. 2016.13(5):898-905.
[65] Su H T,McAvoy T J, Werbos P J. Long-Term Predictive Chemical Processes Using Recurrent Neural Networks [J]. Industrial Application of Chemical Engineering Research, 1992, 31(8): 1338-1352
[66] Buescher K L, Baum C C.A Two-Timescale Approach to Nonlinear Model Predictive Control [J]. Proceedings of American Control Conference. Seatle, 1995: 2250-2256
[67] Najim K, Rusnak A, Meszaros A. Constrained Long-Range Predictive Control Based on Artificial Neural Networks [J]. System Science, 1997, 28(2): 1211-1226.
[68] 刘晓华, 杨振光. 基于动态BP网络误差修正的广义预测控制[J]. 数学的实践与认识, 2002, 32(3): 445-449.
[69] 蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社. 2002
[70] 钱积新, 赵均, 徐祖华. 预测控制[M]. 北京: 化学工业出版社, 2007.
Intelligent Analysis Method and Its Applications in Geotechnical Engineering
GUOJian,YINJun,LITing,QIANJin-dou,KEXiao-Feng,HEZang-Jing
(School of Civil Engineering and Architecture,Wuhan Polytechnic University, Wuhan 430079, China)
With computer technology drastically developing, the intellectual discipline emerged for studying complex problems in order to provide a new approach solving complex system. The research statuses of intelligence algorithm and its applications in geotechnical engineering have been systematically reviewed in this paper. The geotechnical engineering has randomicity, uncertainly and fuzziness due to complex construction condition and external environment. It is almost impossible to accurately analyze failure mechanism and predict security risk in underground engineering. There is an urgent problem to be solved of how to improve the safe reliability, prevent the construction risk and decrease the accident-happening rate in geotechnical engineering. Looking into the future direction of intelligent development and the application prospect in geotechnical engineering, the data fusion technology will be used to develop integrated expert system based on intelligent analysis. It is the inevitable requirement for construction information to predict and control real-time risk.
intelligent analysis; complex system; geotechnical engineering; construction information; prediction control
2017-02-12.
郭健(1968-), 男, 教授, 工学博士, E-mail:guojianxh@163.com.
住建部科学技术项目计划(2015-K3-04).
2095-7386(2017)01-0001-08
10.3969/j.issn.2095-7386.2017.01.001
TU
A
