基于尺寸效应的微径铣刀磨损预测模型的建立与实验研究

孟 杰， 陈小安， 吕中亮， 李 翔

(1.重庆科技学院 机械与动力工程学院，重庆 401331；2.重庆大学 机械传动国家重点实验室，重庆 400044)

基于尺寸效应的微径铣刀磨损预测模型的建立与实验研究

孟 杰1， 陈小安2， 吕中亮1， 李 翔1

(1.重庆科技学院 机械与动力工程学院，重庆 401331；2.重庆大学 机械传动国家重点实验室，重庆 400044)

刀具磨损是影响微细铣削加工的重要因素之一，将材料的本构模型与Usui刀具磨损模型相结合，并考虑到微细加工中存在的尺寸效应，提出一种新的刀具磨损预测模型，采用有限元仿真和物理实验的方法确定硬质合金刀具铣削碳钢时刀具磨损预测模型中的相关参数，并进行了实验验证。为了更直观的观察、预测刀具磨损情况，将该模型应用于微细铣削仿真过程中，可求得任意时刻刀具的磨损及几何轮廓。为微细铣削中刀具磨损的研究提供了新的方法。

微细铣削；微径铣刀；刀具磨损；尺寸效应；刀具磨损预测模型

近年来，随着微小型产品在工业、农业、医疗、军事等众多领域的广泛应用，微细加工技术逐渐成为现代科学研究的前沿和热点。目前，世界各国都已在微细铣削领域展开了广泛的研究。微径刀具是微细加工的重要执行元件，是实现微细铣削的关键技术之一[1-5]。加工过程中刀具的磨损必然会导致其几何尺寸的变化，从而引起铣削力和表面质量的改变，这对微细加工的影响要远大于传统过程，已成为制约微细铣削技术发展的重要因素，因此，微细铣削对刀具性能提出了更高的要求。要实现微细铣削技术的应用和推广，必须对刀具磨损进行研究，分析其对微细铣削过程的影响机制，这也是微细加工研究的关键问题。

目前，国内外许多学者采用各种方法对常规尺度铣削刀具进行了大量的在线监测和刀具寿命的研究。但受加工尺度的影响，微径铣刀的磨损与常规尺度铣削刀具不同，因此已有的关于常规尺度铣削刀具的磨损机理及规律不能直接应用于微径铣刀。而目前对于微径铣刀磨损的研究还比较少：李晓舟等[4]通过高速微细铣削实验，分析了不同主轴转速对刀具磨损的影响;BAO等[6]通过实验拟合的方法建立了考虑刀具磨损的铣削力模型；RAHMAN等[7-8]基于物理实验，采用响应曲面法建立了微细铣削纯铜过程中刀具寿命模型，分析了切削用量对刀具寿命的影响；XIN等[9]通过测量微细刀具前刀面磨损来研究刀具的磨损；赵岩等[10]研究了涂层及非涂层微径铣刀铣削铝时的磨损形式，并分析了切削用量对铣削力的影响；杨凯等[11]研究了涂层铣刀铣削HPb63-3时的磨损状况；ZHU等[12]采用HMM建立了微径铣刀磨损监测模型；陈浩峰等[13]研究了半径为1 mm的金刚石刀具切削CaF2时的磨损情况；张翔等[14]针对单齿切削及两齿交替切削分别建立了隐Markov模型，实现了微径铣刀磨损状态的识别。

上述研究，主要以实验方法为主，研究了微细加工中刀具的磨损及寿命。本文基于微细铣削的尺寸效应，结合有限元法和物理实验，建立适用于微细铣削的刀具磨损预测模型。

1 微径铣刀磨损预测模型的建立

刀具是保证加工质量的重要环节，为了提高微细铣削的加工质量，必须对微径铣刀的磨损进行研究。刀具磨损实验通常需要花费大量的人力和时间、消耗大量的材料，同时加工条件的复杂性也使刀具的磨损比较复杂。采用有限元仿真的方法来模拟金属切削过程，能够达到所需的精度，具有很高的可靠性，并且仿真结果形象、直观，已成为研究微细加工过程的有效工具。

1.1 刀具磨损率模型的修改

USUI等[15]假设刀具前刀面月牙洼磨损主要由粘结磨损造成，将能量法、实验法与有限差分法结合，建立了硬质合金刀具切削碳钢时的磨损模型，并通过切削实验确定了模型中的常数。继而，采用该模型对前刀面的月牙洼磨损进行了预测，与实验结果基本相符。该模型揭示了特定加工条件下，磨损增长率与相对滑动速度、接触正压力、切削温度等切削变量之间的关系。后来，KITAGAWA等[16]的研究表明，Usui模型也适用于由磨粒磨损造成的后刀面磨损。

Usui刀具磨损率模型为：

(1)

微细铣削与传统铣削尽管在运动学上是相同的，但由于加工尺度的缩小会产生尺寸效应。尺寸效应使微细加工的切削力比常规加工大的多，加工过程更加困难。从力学角度研究尺寸效应，涉及切削力、刀具磨损、切屑形成等方面。从微径铣刀角度来看，不但刀具的几何尺寸变化较大，而且刀具的加工性能、磨损速度、失效形式都要受到影响。因此，考虑到微细铣削过程中存在的尺寸效应，对式(1)进行修改，引入尺寸效应系数，建立适用于微径铣刀的磨损预测模型：

(2)

式中，CSE为应力的尺寸效应系数，与加工条件有关。

1.2 微细铣削有限元仿真

采用ABAQUS/CAE建立直径为100μm的硬质合金两刃螺旋立铣刀微细铣削碳钢AISI4340的二维仿真模型。根据铣刀切削刃的对称性和加工过程的特点，将模型简化为一个铣削刃对工件的微细铣削，其中刀具刃口的钝圆半径(0.5μm)、刀具径向前角和后角(12°和30°)、螺旋角(35°)均按实际尺寸建模。工件材料AISI4340是一种中碳低合金钢，强度高、淬透性好。在微细铣削过程中，由于应变梯度塑性理论能够很好的解释在微观尺寸下材料强度随尺寸减小而增大的现象，因此采用应变梯度塑性理论描述工件材料AISI4340的本构关系，相关参数如表2所示。选用位移-温度双线性、带沙漏控制的四边形四节点单元对模型进行网格划分，并结合分析步中的任意拉格朗日-欧拉(ALE)网格自适应技术，对微细铣削过程进行热机耦合分析，如图1所示。

当微细铣削参数分别取表3所列三组数据时，采用上述有限元模型进行仿真，图2为第一组数据仿真到24.5μs时形成的切屑和应力云图。然后，使用Python语言对仿真结果进行处理，从中提取刀具磨损模型中所需参数vs,σf和θ，列于表4。从表4中可以看出，微细铣削过程中的切削温度低于1 000K，因此，取C=7.8×10-9m2/MN、λ=5.302×103K，则：

(3)

图1 有限元模型Fig.1 FE model

材料参数A/MPa材料参数B/MPa材料参数n材料参数C材料参数m熔化温度Tm/℃剪切模量G/GPaBurgers向量b/nm经验系数α位错密度参数μ7925100.260.01401.031520800.2480.50.38

表3 微细铣削仿真和实验参数Tab.3 Micro milling simulation and experiment parameters

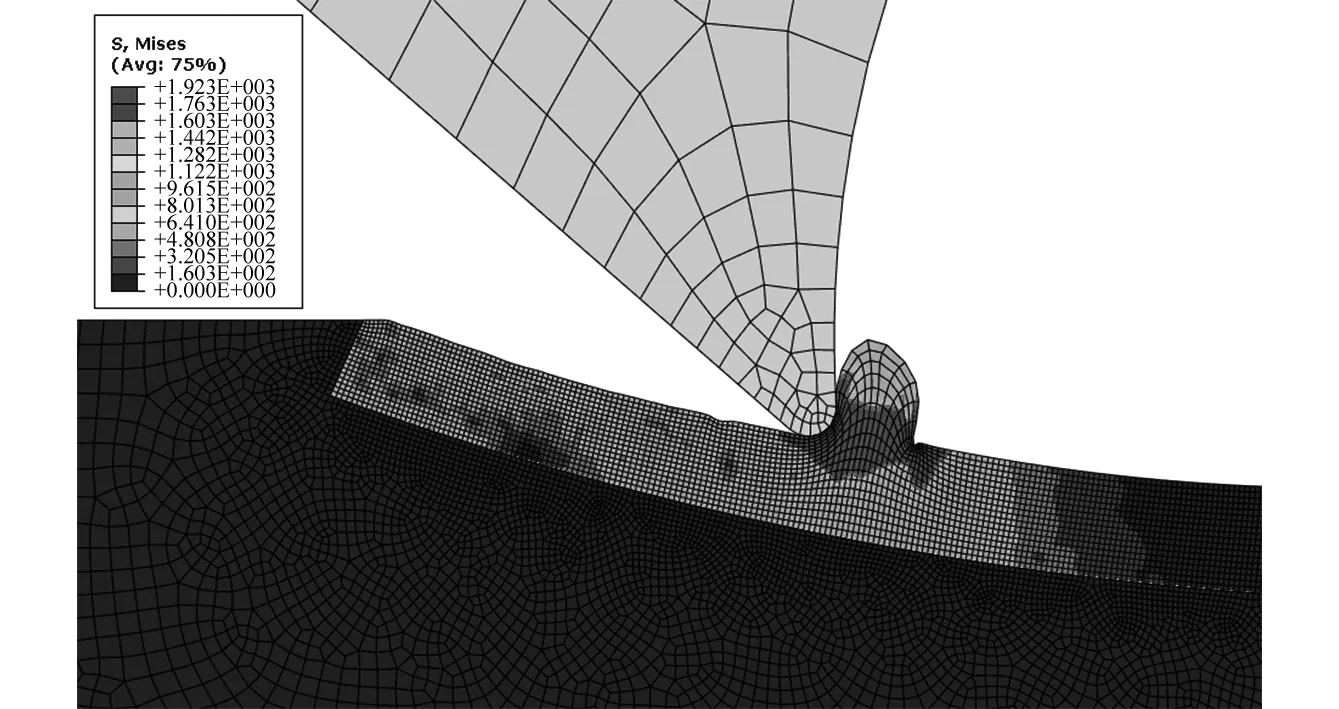
图2 t=24.5 μs微细铣削仿真Fig.2 Chip formation simulation at t=24.5 μs

1.3 微细铣削实验及模型验证

微细铣削实验在三轴数控铣床上进行，主轴最高转速为90 000 r/min，工作台移动分辨率为1 μm，机床夹具上装有工作频率范围为100～1 000 kHz的声发射传感器，并配有相应的前置放大器、数据采集卡，可用于检测铣削过程中刀具与工件的接触情况。按照表3所示参数，采用三把新刀具(均为TS-2-0040-S微径两刃螺旋立铣刀)，分别完成三组微细铣削AISI 4340的加工实验，最后使用扫描电子显微镜(SEM)来观测刀具的磨损，如图3所示，测量结果列于表5。

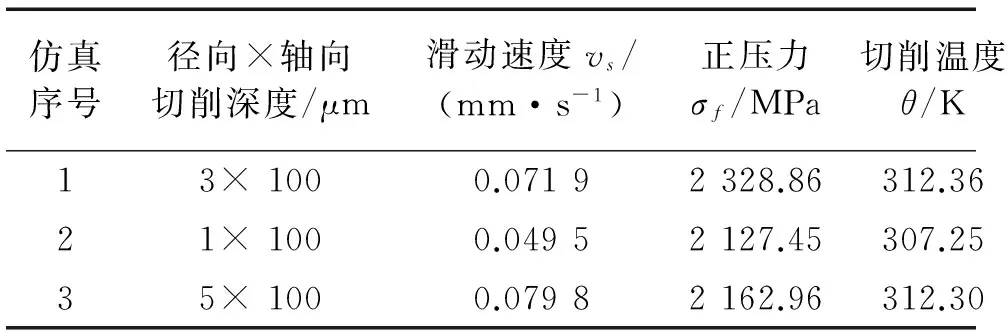
表4 微细铣削仿真结果Tab.4 Parameters from micro milling simulation result

表5 微径铣刀磨损量Tab.5 Wear rate of micro milling tool

将仿真1及其相应实验1所得数据代入式(3)计算，求得CSE。

CSE= 3.41×109

图3 刀具磨损SEM图Fig.3 Tool wear from SEM

因此，采用硬质合金刀具加工AISI 4340时，刀具磨损预测模型为：

(4)

分别将仿真2、3得到的数据代入式(4)计算刀具的磨损率，并与其相应实验2、3所得结果进行比较。

仿真2：

8.97×10-5mm/s

实验2：

误差：

仿真3：

1.94×10-4mm/s

实验3：

误差：

从以上结果可以看出，仿真3所得结果与实验3结果之间的误差较小，在可接受范围内；而仿真2的误差较大，这是因为在实验2中，由于切深太小(1 μm)，微细铣削过程中出现了犁切现象，刀具磨损也比较小，使得实验结果和微细铣削仿真结果差异较大。因此，刀具磨损预测模型式(4)适用于微径刀具的正常铣削过程。

2 微径铣刀磨损预测模型的应用及验证

将所建立的刀具磨损预测模型与有限元模型结合，可获得仿真过程中刀具在任意时刻的磨损量及几何轮廓。

2.1 微径铣刀磨损的预测

首先，采用1.2节所建立的有限元模型进行仿真，如图4(a)所示，其中，切削用量取值为：主轴转速60 000 r/min，进给量100 mm/min，背吃刀量4 μm，径向切削深度100 μm。取刀具铣削刃上参与加工的部分为分析对象，并对该部分节点进行编号如图4(b)所示，预测经1.5 min铣削后刀具的磨损量。

然后，从仿真结果中提取刀具铣削至1.5 min时各节点的相对滑移速度vs、正应力σf和切削温度θ，代入式(4)，计算各节点的磨损率，从而得到节点位移；再结合节点的位移方向(前刀面上节点位移方向为垂直于刀具与工件的相对滑移速度方向，后刀面上节点位移方向为相对滑移速度方向)，得到各个节点的位移矢量。

最后，根据节点位移矢量重构刀具轮廓，图4(c)、(d)为刀具磨损前后几何轮廓的对比图。在有限元软件中测得此时微径铣刀磨损量约为7.921 μm。由于仿真过程中忽略了外部因素的变化和影响，因此可认为微径铣刀两切削刃磨损量相等，仿真所得铣削刃上各节点的位移矢量为两切削刃上相应位置位移矢量的平均值，所以刀具总磨损量为15.842 μm。

(a)

(b)

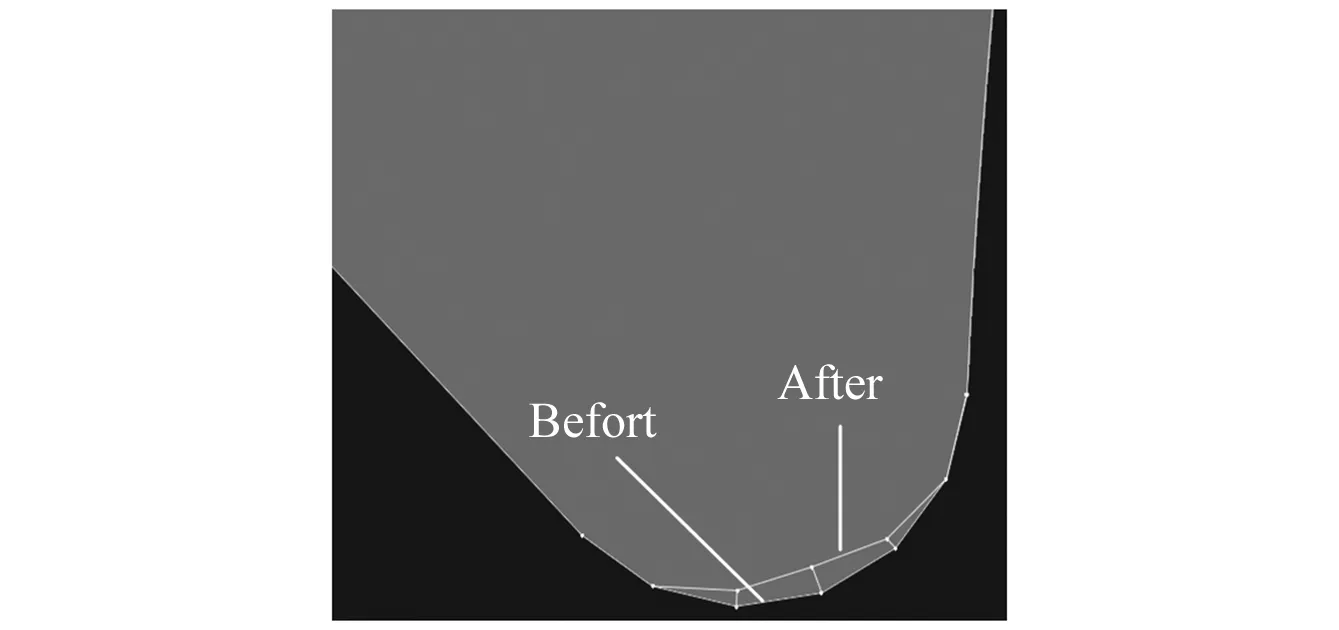
(c)

(d)

2.2 微径铣刀磨损预测的实验验证

采用1.3节的实验设备及2.1节仿真参数进行微细铣削实验，加工至1.5 min时将刀具取下，在SEM下进行观察。图5为SEM所拍摄的刀具磨损图，其中5(a)为刀具切削部分放大1 000倍后的整体截面图，5(b)和(c)分别为两切削刃放大3 500倍后的局部视图。从图中可以看出：

(1)加工后刀具两切削刃上不同程度的粘结了部分切屑，但仍然可以观察到刀具两切削刃磨损程度不同。在图5(b)和(c)中可分别测出铣削刃1的磨损量为11.053 μm，铣削刃2的磨损量为4.056 μm，这可能是由于以下原因造成的：①刀具制造过程中，尺寸误差和加工误差使两切削刃的形状并非完全相同；②刀具安装时其轴线与铣床主轴轴线没有完全重合，存在少量偏差；③微细铣削过程中的颤振现象。

(2)与传统铣削过程中刀具磨损不同，微径铣刀两个切削刃的刀尖部分磨损严重，主要是因为微细铣削时刀具刃口的钝圆半径与切削厚度在同一数量级，切削时刀具前角为负前角，剪切运动主要发生在刀尖附近。

(3)通过测量得到的刀具总磨损量为15.109 μm，因此，磨损预测模型的误差为：

可见，所建立的刀具磨损预测模型能够成功的应用于有限元仿真过程中，并通过仿真可以较准确的预测给定铣削条件下刀具在任意时刻的磨损量及平均几何轮廓。

图5 刀具磨损SEM图Fig.5 Tool wear from SEM

3 结 论

(1)微细加工由于切削尺寸的缩小，使传统的切削理论无法直接用于微细铣削过程，本文基于尺寸效应，结合微细铣削的特点，建立微径铣刀磨损的预测模型。

(2)微径铣刀磨损预测模型中系数的取值受刀具和被加工材料的影响，本文通过物理实验和有限元仿真的方法确定了硬质合金微径刀具铣削AISI 4340时，微径铣刀磨损预测模型中的常数，并进行了实验验证。

(3)将微径铣刀的磨损预测模型用于微细铣削有限元仿真过程，完成了对仿真过程中刀具磨损的预测，并重构刀具轮廓，与实验结果基本吻合，具有一定的指导意义。

[ 1 ] 李红涛, 来新民, 李成锋,等. 介观尺度微型铣床开发及性能试验[J]. 机械工程学报，2006,42(11):162-167. LI Hongtao, LAI Xinmin, Li Chengfeng, et al. Development of meso-scale milling machine tool and its performance analysis[J]. Journal of Mechanical Engineering,2006,42(11): 162-167.

[ 2 ] DE CRISTOFARO S, FUNARO N, FERITI G C, et al. High-speed micro-milling: novel coatings for tool wear reduction[J]. International Journal of Machine Tools & Manufacture, 2012, 63(4):16-20.

[ 3 ] SAEDON J B, SOO S L, ASPINWALL D K, et al. Prediction and optimization of tool life in micromilling AISI D2(～62HRC) hardened steel[J]. Procedia Engineering, 2012, 41(41):1674-1683.

[ 4 ] 李晓舟，马秋瀚. 微细铣削刀具的磨损机理实验[J]. 机械科学与技术, 2013,32(8):1235-1238. LI Xiaozhou，MA Qiuhan. Experimental study on wear mechanism of micro milling tool[J]. Mechanical Science and Technology for Aerospace Engineering, 2013,32(8):1235-1238.

[ 5 ] 弯艳玲, 张学蕊, 于化东,等. 高速微铣削铝合金表面粗糙度的多指标正交试验研究[J]. 中国机械工程, 2013,24(24):3278 -3282. WAN Yanling, ZHANG Xuerui, YU huadong, et al. An multi-index orthogonal test study of aluminum alloy surface roughness using high speed micro-milling process[J]. China Mechanical Engineering, 2013,24(24):3278-3282.

[ 6 ] BAO W Y, TANSEL I N. Modeling micro-end-milling operations. partⅢ: influence of tool wear[J].International Journal of Machine Tools & Manufacture, 2000, 40(5):2193-2211.

[ 7 ] RAHMAN M, KUMAR A S, PRAKASH J R S. Micro milling of pure copper[J]. Journal of Materials Processing Technology, 2001, 116: 39-43.

[ 8 ] RAHMAN M A , RAHMAN M, KUMAR A S, et al. CNC microturning: an application to miniaturization[J]. International Journal of Machine Tools & Manufacture, 2005, 45(6):631-639.

[ 9 ] LIN X , ZHAO X P, CHEN J, Tool wear prediction in micro-end-milling with hard material[J]. Journal of Shanghai Jiaotong University, 2007,12(3):359-363.

[10] 赵岩, 梁迎春, 白清顺,等. 微细加工中的微型铣床、微刀具磨损及切削力的实验研究[J]. 光学精密工程, 2007,15(6): 894- 902. ZHAO Yan, LIANG Yingchun, BAI Qingshun, et al. Micro-milling machine tool, micro-tool wear and cutting forces in micro- machining[J]. Optics and Precision Engineering, 2007, 15(6):894-902.

[11] 杨凯, 白清顺, 梁迎春,等. 微细铣削铅黄铜时微径铣刀的损伤研究[J]. 摩擦学学报, 2008, 28(5) : 448-452. YANG Kai, BAI Qingshun, LIANG Yingchun, et al. Damage of micro-diameter cutter while micro-milling hpb63-3 lead brass[J]. Tribology, 2008, 28(5) : 448-452.

[12] ZHU K P, WONG Y S, HONG G S. Multi-category micro-milling tool wear monitoring with continuous hidden Markov models[J]. Mechanical Systems and Signal Processing, 2009, 23(2):547-560.

[13] 陈浩峰, 王建敏, 戴一帆,等. 超精密切削氟化钙单晶金刚石刀具磨损研究[J]. 中国机械工程, 2011, 22(13):1519-1522. CHEN Haofeng, WANG Jianmin, DAI Yifan, et al. Research on diamond tool wear in ultra-precision cutting of caf2 crystals[J]. China Mechanical Engineering, 2011, 22(13):1519-1522.

[14] 张翔, 富宏亚, 孙雅洲,等. 基于隐Markov模型的微径铣刀磨损监测[J]. 计算机集成制造系统, 2012,18(1):141-148. ZHANG Xiang, FU Hongya, SUN Yazhou, et al. Hidden Markov model based micro-milling tool wear monitoring[J]. Computer Integrated Manufacturing Systems, 2012,18(1): 141-148.

[15] USUI E, SHIRAKASHI T, KITAGAWA T. Analytical prediction of three dimensional cutting process, part 3: cutting temperature and crater wear of carbide tool[J]. Trans ASME J Eng Mater Technol, 1978, 100:236-243.

[16] KITAGAWA T, MAEKAWA K, SHIRAKASHI T, et al. Analytical prediction of flank wear of carbide tools in turning plain carbide steels, part 1: characteristic equation of flank wear[J]. Bull Japan Soc of Prec Eng, 1988, 22(4): 236-269.

Establishment and experimental study of a wear prediction model of micro milling toolin consideration of the size effect

MENG Jie1, CHEN Xiao’an2, LÜ Zhongliang1, LI Xiang1

(1.College of Mechanical and Power Engineering, Chongqing University of Science and Technology, Chongqing 401331, China;2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)

Tool wear is one of the important factors that affect the micro milling process. Combining the constitutive model and Usui tool wear model, and considering the size effect during micro machining, a new tool wear prediction model was proposed. The relevant parameters of the prediction model for the micro milling of carbon steel workpieces by tungsten carbide tools were determined by the finite element simulation and physical experiment, which were then verified by further experiments. In order to observe and predict the tool wear more apparently, the prediction model was applied yet to a micro milling process simulation, so as to obtain the tool wear and its geometrical shape at any time in the proccss. The study provides a new method for studying the tool wear during micro milling.

micro milling; micro milling tool; tool wear; size effect; tool wear prediction model

国家自然科学基金(51505049);重庆市基础与前沿研究计划项目(CSTC2013JCYJA70004);重庆市教委科学技术研究项目(KJ1501314)

2016-06-13 修改稿收到日期：2016-07-26

孟杰 女，博士，副教授，1981年生 E-mail：mj8101@163.com

TG501

A

10.13465/j.cnki.jvs.2017.06.036