高速公路护栏立柱导波相位特性分析与试验研究

柳伟续， 唐志峰， 吕福在， 乔印虎, 张春雨

(1.安徽科技学院 机械工程学院 安徽 滁州 233100；2. 浙江大学 数字技术与仪器研究所 杭州 310027；3. 浙江大学 现代制造工程研究所 杭州 310027)

高速公路护栏立柱导波相位特性分析与试验研究

柳伟续1， 唐志峰2， 吕福在3， 乔印虎1, 张春雨1

(1.安徽科技学院 机械工程学院 安徽 滁州 233100；2. 浙江大学 数字技术与仪器研究所 杭州 310027；3. 浙江大学 现代制造工程研究所 杭州 310027)

为了实现对高速公路立柱端面导波信号的自动识别，进而实现立柱的埋深检测，对立柱端面处导波信号的相位特性进行了分析研究。通过推导计算反射系数得出端面回波信号与激励脉冲信号反相的相位特性。采用基于Gabor字典的匹配追踪算法分别对ABAQUS有限元仿真信号和实测导波信号进行了稀疏分解,通过所得匹配原子的相位参数验证了回波信号的相位特性，其中实测信号为分别用64 kHz和128 kHz的T(0,1)模态导波对埋地立柱和自由立柱进行检测所得。仿真与实测信号的试验结果与理论分析相吻合，回波信号的相位特性为导波检测中的信号处理技术提供了新的途径和方法。

超声导波技术；相位特性；匹配追踪；护栏立柱；信号提取

发生交通事故时，高速公路护栏在减缓车速、防止车辆冲出路面或驶向对向车道从而避免造成二次交通事故方面具有重要意义。由于施工单位的不规范操作(偷工减料等)、立柱的腐蚀等导致的立柱埋深不够成为了道路交通安全的重大隐患。因此，很有必要对护栏立柱的埋置深度进行检测。目前高速公路立柱埋深无损检测技术已取得一定研究基础，何存富等[1]对高速公路立柱埋深检测的导波模态进行了研究，贾志绚等[2]实现了基于弹性波法的高速公路立柱埋深检测系统，龚廉溟等[3]对高速公路立柱埋深检测专用传感器进行了研究。实际检测时，由于信号的多次反射、叠加和引入的噪声等导致检测信号中端面信号难以判断，为此文章对高速公路立柱端面处导波信号的相位特性进行了研究，为利用相位特性实现立柱端面信号的自动识别和提取做好准备。

超声导波检测技术作为一种长距离、大范围的有效检测方法，以其无损、快速和可靠的特点正被广泛应用于石油、化工等领域[4-6]。导波检测信号中含有检测构件丰富的特征信息，如构件的端面、焊缝、法兰等几何特征信息，考虑到导波信号传播过程中的衰减、频散、多模态及引入的噪声等因素，导致检测信号复杂，如何实现对特征信息的自动识别和提取一直都是导波信号处理的难点。在导波的实际检测中，根据检测信号的波形特点发现了不同声阻抗结构回波信号的相位差异[7]，但目前对这种导波相位差异的理论分析、试验研究以及实际应用的文章和例子都还很少[8-9]，本文拟对高速公路立柱的相位特性进行分析和试验研究。

文章通过推导计算反射系数分析了立柱端面处导波信号的相位特点，得到端面回波信号与激励信号的相位关系，为了从检测信号中得到端面回波信号的相位信息，介绍了匹配追踪算法(Matching Pursuit，MP)[10]，实现对检测信号的稀疏分解和特征信息的提取。最后对有限元仿真信号和实测信号进行了端面回波信号的相位提取和验证研究，并对实验结果进行了分析总结和应用展望。

1 公路立柱端面处导波信号相位特性分析

首先，分析入射信号与反射信号的关系。如图1所示，设由激励信号在立柱中产生的脉冲导波信号(入射信号)为si(t)，传播过程中遇到声阻抗发生变化时，比如立柱端面，导波信号就会反射，其回波(反射)信号的时域波形可表示为：

(1)

式中，Si(ω)为si(t)的傅里叶变化，R(ω)为反射系数，其表达式可以表示为：

(2)

图1 立柱中导波传播示意图Fig.1 Propagation illustration of guided wave in guardrail post

其次，得到立柱的反射系数。设入射信号和反射信号的幅值分别为Ai和Ar，则根据反射系数定义有：R=Ai/Ar。在立柱中，将导波看作在声阻抗为Z1=ρ1v1A1的波导中传播的平面波，其中ρ1为立柱密度，v1为波速，A1为管壁横断面积，则导波在声阻抗发生改变处，其反射系数可进一步表示为[11]：

(3)

式中,Z2为发生改变的声阻抗。

最后，推导计算反射系数得出相位关系。假设此立柱上有一凹槽，其所在管壁横断面积为A2，则凹槽处声阻抗为Z2=ρ1v1A2，将其代入式(3)化简可得：

(4)

可见反射系数由横断面积的比值决定，而立柱的端面可以看作凹槽的横断面积A2→0的情况，则端面处反射系数为：

(5)

(6)

式中，θRe,θIn分别为端面处回波信号和入射信号的相位，即端面处回波信号与入射信号相位相反。

综上分析，表征立柱几何特征的端面回波信号与激励信号反相。然而实际测得的导波信号，由于噪声和多次反射等导致无法直接读出端面回波的相位信息，故为验证和应用上述相位特点，需先对导波检测信号进行特征分解得到端面信号的相位信息，下面先介绍匹配追踪稀疏分解算法。

2 相位提取算法分析

匹配追踪算法作为一种贪婪算法，通过迭代实现信号的特征提取和稀疏表示，算法描述如下:

设D={gτ}τ∈Γ为希尔伯特空间H中的过完备字典，gτ是具有单位能量的原子(‖gτ‖=1)。在匹配字典上，经过N次迭代后，原信号可以稀疏表示为：

(7)

式中，xN为当前信号的稀疏表示，RNx为信号余量即残差。具体步骤：

步骤1 初始化残差信号R0x=x，最佳原子集为V0空集，设置迭代次数T(T>0)，迭代计数c=0；

步骤2 计算内积{〈Rkx,gτ〉}τ∈Γ，使下式内积最大(即残差最小)遍历得到最佳原子gτk+1∈D：

(8)

其中最优比例因子α∈(0,1]；

步骤3 更新迭代次数c=c+1和最佳原子集Vk+1=Vk∪{gτk+1}，计算Rkx在gτk+1上投影得到K+1次信号稀疏表示和新的残差信号：

xk+1=xk+〈Rkx,gτk+1〉gτk+1

(9)

Rk+1x=Rkx-〈Rkx,gτk+1〉gτk+1

(10)

步骤4 如果迭代次数满足c≥T，则结束迭代；否则将K+1代入K，重复执行步骤2～4；完成迭代后，将式(10)从k=0到c-1求和得到信号x在V∈D上稀疏表示：

(11)

用于导波检测的激励脉冲信号，我们选用具有良好时频聚焦性的Gabor脉冲信号：

gGr(t)=exp-t2/(2σ2)cos(2πfct+θ)

(12)

式中σ、fc和θ分别为脉冲宽度、中心频率和相位。根据式(1)、(2)已知，回波信号相对于激励信号只是幅值和相位发生了改变，故当激励信号采用Gabor脉冲信号时，得到的回波信号也将是Gabor信号，因此，用于上述匹配追踪算法的匹配原子采用Gabor字典，为了有效匹配回波信号的相位参数φ，这里采用复数形式的Gabor原子：

(13)

式中，g(t)=e-t2/2是Gauss窗函数，参数Γ=(s,u,fc)表示原子的尺度因子、时间中心和频率中心。迭代所得匹配原子的相位参数：

φi=arg(〈Rif,gτi(ui,si,fci)〉)

(14)

此相位也是所匹配回波信号的相位。

迭代结束后，将根据激励信号的相位和式(6)表明的相位关系，从c次迭代所得的原子集中，提取出满足端面回波相位关系的最佳原子，进行相位的验证和端面回波的自动识别。

3 立柱端面信号相位特性验证

3.1 有限元仿真信号验证

在ABAQUS仿真软件中，按表1示A级波形梁护栏立柱参数[12]，建立得到立柱的物理模型。

表1 护栏立柱几何、物理参数Tab.1 Geometrical and physical parameters of Guardrail post

模拟T(0,1)模态导波对立柱进行有限元仿真，激励信号为式(12)的Gabor脉冲信号。根据T(0,1)模态导波的波结构，该模态下质点振动只存在圆周方向(即柱坐标下的θ方向)的位移，且沿壁厚方向位移分布均匀，因此对立柱端面所有节点施加θ方向的位移载荷，可以模拟T(0,1)模态导波。激励参数取φ=0 rad、fc=64 kHz和σ=1.50×10-5，在立柱的同一端施加载荷并接收回波信号，得到的仿真波形如图2所示。

图2 仿真结果Fig.2 Simulation result

进行信号匹配分解时，为了避免初始信号的影响，取出端面回波信号得到图3(a)所示的待匹配信号，通过MATLAB编程实现的基于Gabor字典的匹配追踪算法，对其进行稀疏分解，经过一次迭代之后，得到的匹配原子和重构信号分别如图3(b)和(c)所示。

经过迭代，得到的最佳原子参数如表2所示。

(a) 待匹配信号

(b) 匹配原子

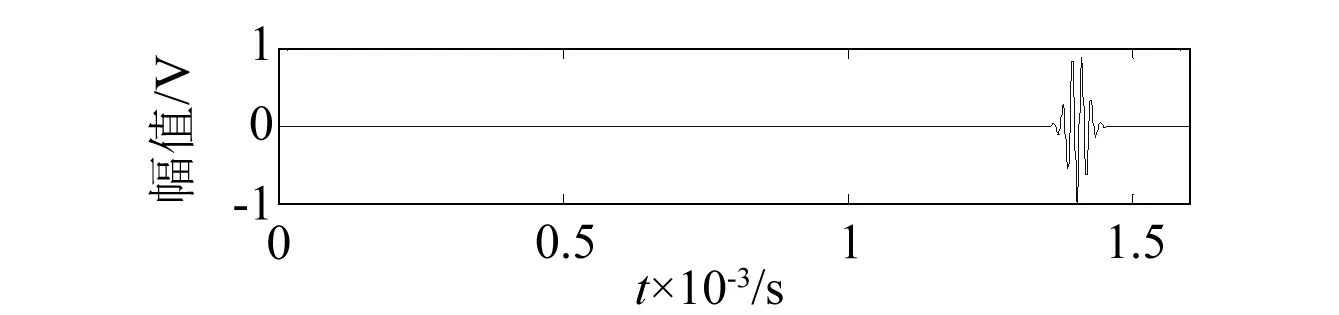
(c) 重构信号

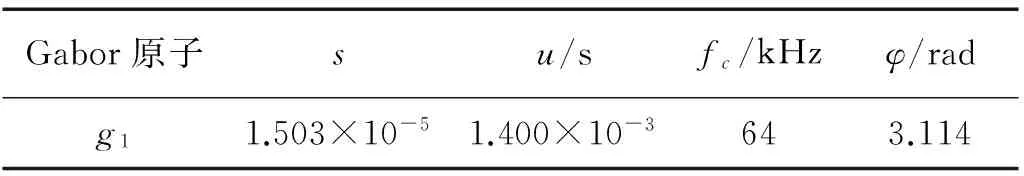
Gabor原子su/sfc/kHzφ/radg11.503×10-51.400×10-3643.114

通过稀疏分解得到了端面回波的最佳匹配原子g1，匹配原子的相位参数φ=3.114 rad即为回波信号的相位，结合激励信号φ=0 rad知与式(6)相位关系的理论值基本吻合。

3.2 公路立柱实测信号相位特性验证

相对于其他模态导波，本文选用具有良好频散和传播特性的T(0,1)扭转模态导波对实验立柱进行导波检测[13]。图4为高速公路立柱导波无损检测示意图。所用A级波形梁实验立柱：全长S=2.150 m，外径140mm，壁厚4.5mm，导波换能器距离立柱顶端距离d=41 cm。利用课题组研发的高速公路立柱超声导波检测仪MLGW300，对其进行无损检测。激励信号为Gabor脉冲信号，相位取φ=0 rad。

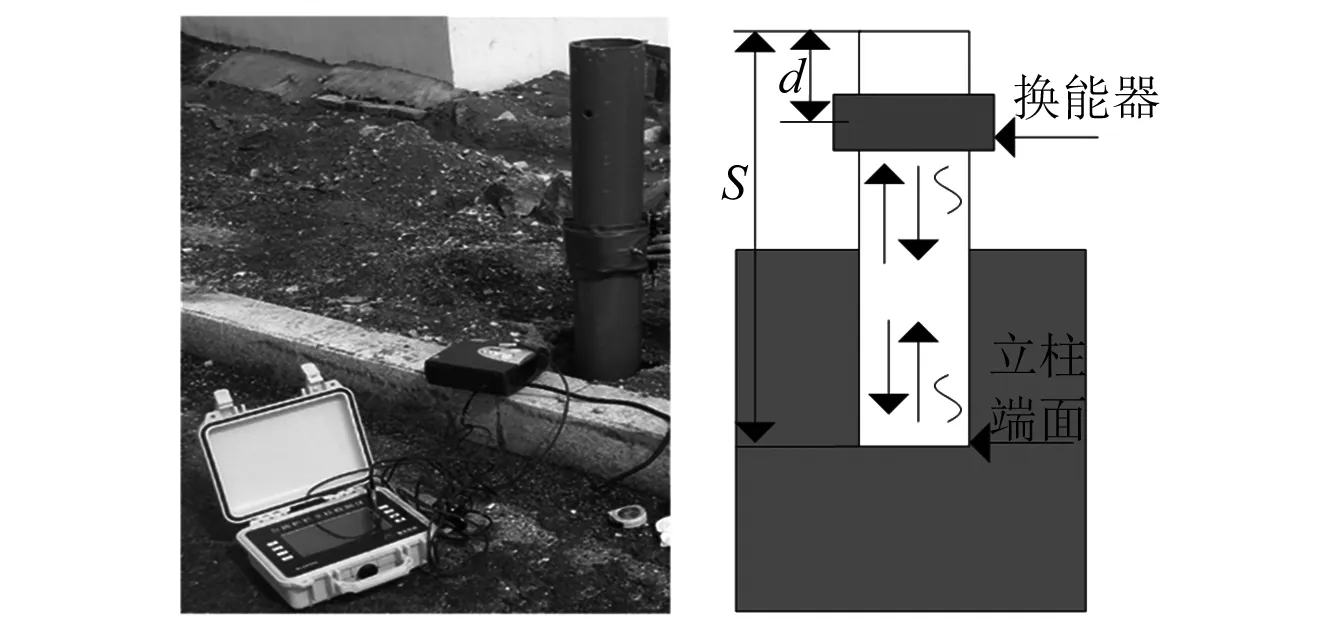
图4 公路立柱检测示意图Fig.4 Inspection illustration of guardrail post

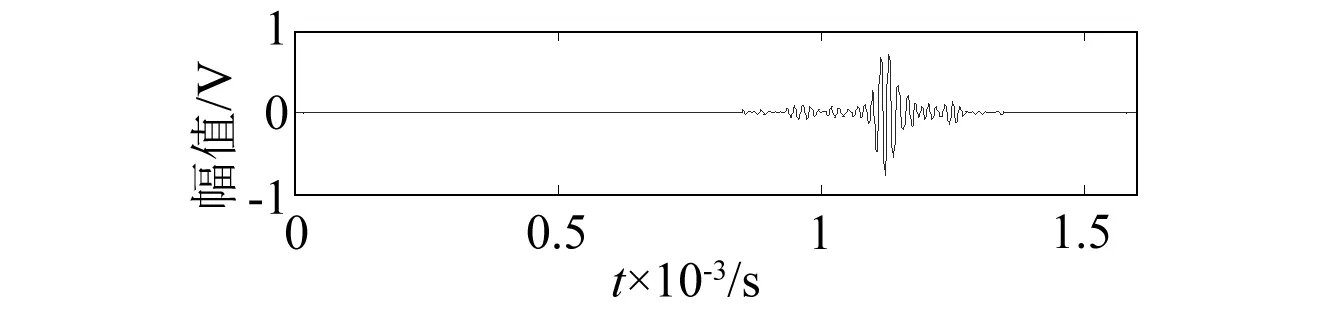
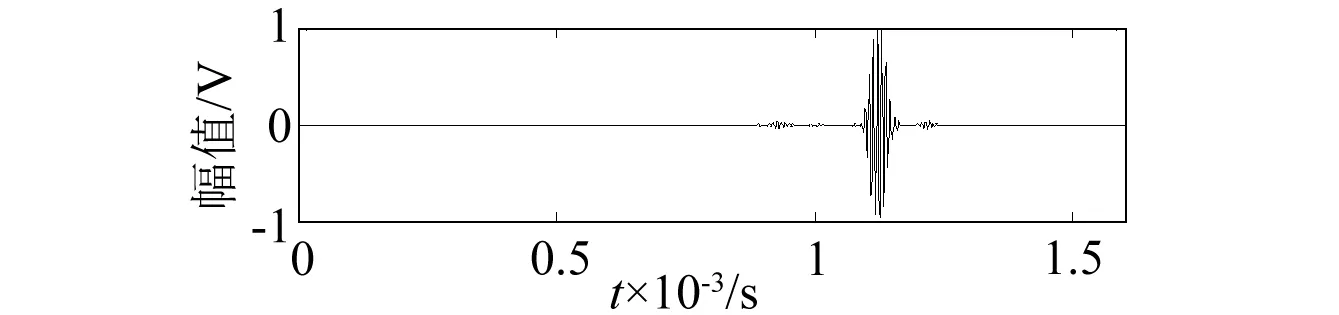
在立柱埋地之前和埋地之后(立柱埋深1.20m)，分别用fc=64 kHz和fc=128 kHz的T(0,1)模态导波对其进行检测，所得检测信号如图5(a)、(b)、(c)和(d)所示。

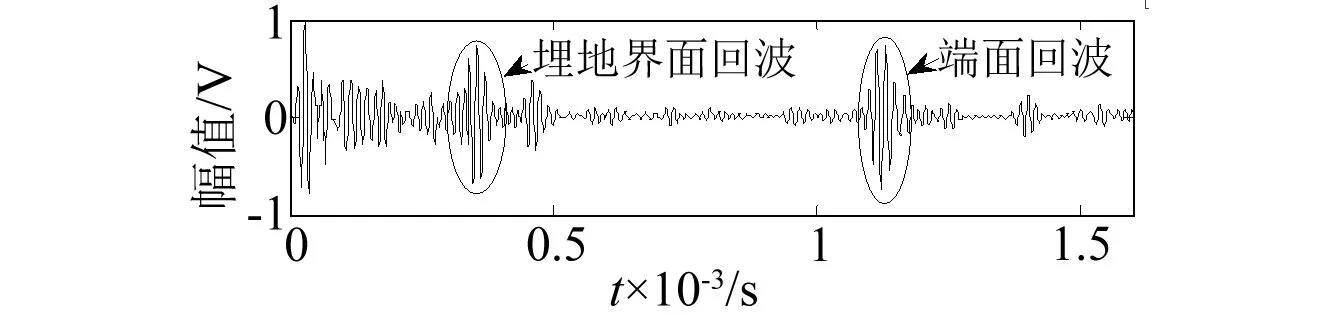
(a)64 kHz埋地

(b)64 kHz拔出

(c)128 kHz埋地

(d)128 kHz拔出

观察图5中各检测信号波形：对于图(b)、(d)自由立柱(埋地之前)检测信号中主要是初始信号、端面处第一次回波信号及其到达立柱上端面后的多次反射信号；而埋地立柱图(a)、(c)检测信号中，除了具有自由立柱检测时的信号波形之外，还有来自埋地界面处的回波信号和立柱上端面的多次反射信号。进行相位算法提取时，为了避免干扰，取出检测信号中的端面信号部分，得到图6所示各待匹配信号，通过MATLAB实现的基于Gabor字典的匹配追踪算法，分别对其进行匹配分解。

(a)64 kHz埋地

(b)64 kHz拔出

(c)128 kHz埋地

(d)128 kHz拔出

各自经过一次迭代后，得到的最佳匹配原子波形分别如图7(a)、(b)、(c)和(d)所示。

表3所示为经过迭代所得图7中各最佳匹配原子的参数。

表3 匹配追踪所得最佳原子参数Tab.3 Parameters of optimum atom by matching pursuit

(a)64 kHz埋地

(b)64 kHz拔出

(c)128 kHz埋地

(d)128 kHz拔出

图8 相位的理论值与实验值Fig.8 The theoretical and experimental value of phase

图9所示为相位提取算法中，根据上述最佳匹配原子按照式(9)所得各自重构信号，即为检测信号中端面回波信号的最佳匹配信号。

(a)64 kHz埋地

(b)64 kHz拔出

(c)128 kHz埋地

(d)128 kHz拔出

4 结 论

文章通过分析反射系数，对立柱中端面处导波信号的相位特性进行了试验研究，并通过有限元仿真信号和实测信号进行了理论分析所得相位结论的验证，所得试验结果与理论分析相吻合，满足工程要求。为接下来，根据导波相位特性自动识别和提取端面信息，实现高速公路立柱埋深检测做好准备。

通过对导波相位特性的有益尝试，实现了对检测信号的识别和特征提取，拓展了导波信号自动识别和提取的方法。端面处回波信号的相位特性可以进一步推广用于各类管材、棒材等导波研究领域特征信号的识别和提取。同时为了进一步提高检测方法的精度，接下来还需从提高检测信号的信噪比和更优的稀疏分解算法两个方面进行深入研究。

[ 1 ] 何存富, 王学浦, 王秀彦,等. 基于导波技术的高速公路护栏立柱埋深检测[J]. 中国公路学报, 2008, 21(6): 37-42. HE Cunfu, WANG Xuepu, WANG Xiuyan, et al. Inspection of expressway guardrail post length partly embedded in soil based on ultrasonic guided wave technology[J]. China Journal of Highway and Transport, 2008, 21(6): 37-42.

[ 2 ] 贾志绚, 张潇, 赵星,等. 基于弹性波法的公路护栏立柱埋深无损检测技术及影响因素研究[J]. 北京工业大学学报, 2012(6):870-874. JIA Zhixuan, ZHANG Xiao, ZHAO Xing, et al. Research on influence factors and ndt technology of expressway barrier post embedded depth in soil based on the elastic wave technique[J].Journal of Beijing University of Technology, 2012(6):870-874.

[ 3 ] 龚廉溟, 胡富翔, 曹德洪, 等. 高速公路护栏立柱超声导波检测专用传感器夹具研制[J]. 公路, 2010 (9): 212-214. GONG Lianming, HU Fuxiang, CAO Dehong, et al. The special ultrasonic guided wave inspection sensor fixture development of highway guardrail post [J].Highway, 2010 (9): 212-214.

[ 4 ] ALLEYNE D N, PAVLAKOVIC B, LOWE M J S, et al. Rapid, long range inspection of chemical plant pipework using guided waves[J]. Key Engineering Materials, 2004, 270: 434-441.

[ 5 ] CAWLEY P, CEGLA F, GALVAGNI A. Guided waves for NDT and permanently-installed monitoring[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2012, 54(11): 594-601.

[ 6 ] ROSE J L, CHO Y, AVIOLI M J. Next generation guided wave health monitoring for long range inspection of pipes[J]. Journal of Loss Prevention in the Process Industries, 2009, 22(6): 1010-1015.

[ 7 ] User’s manual for MsS data analysis and reporting software for piping inspection (Version 2006) [R]. US: Southwest Research Institute, 2006：24-25.

[ 8 ] KWUN H, KIM S Y, CHOI M S. Experimental comparison of analytical modeling of a guided-wave interaction with a notch in a pipe[J]. Journal of the Korean Physical Society, 2004, 45(2): 380-385.

[ 9 ] KIM S Y, KWUN H. Method for automatic differentiation of weld signals from defect signals in long-range guided-wave inspection using phase comparison[P]. US. Patent 7565252, 2009.

[10] MALLAT S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. Signal Processing, IEEE Transactions on, 1993, 41(12): 3397-3415.

[11] CHOI M S, KIM S Y, KWUN H, et al. Transmission line model for simulation of guided-wave defect signals in piping[J]. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on, 2004, 51(5): 640-643.

[12] 公路交通安全设施设计技术细则:JTG/T D81—2006[S]. 北京：交通部公路科学研究院，2006.

[13] LOWE M J S, CAWLEY P. Long range guided wave inspection usage-current commercial capabilities and research directions[R]. London: Imperial College London, 2006.

Phase characteristic analysis and experimental study on the guidedwave reflected from expressway guardrail posts

LIU Weixu1, TANG Zhifeng2, LÜ Fuzai3, QIAO Yinhu1, ZHANG Chunyun1

(1. College of Mechanical Engineering，Anhui Science and Technology University, Chuzhou 233100,China;2. Institute of Advanced Digital Technologies and Instrumentation, Zhejiang University, Hangzhou 310027,China;3. Institute of Modern Manufacture Engineering, Zhejiang University, Hangzhou 310027,China)

In order to identify automatically the guided wave signal reflected from the end of an expressway guardrail post and further inspect the buried depth of the guardrail post, the phase characteristic of the guided wave at the end of the guardrail post was analyzed and investigated. It is concluded that the echo signal from the end face has the characteristic of reverse-phase with the excitation pulse signal through deducing and calculating the reflection coefficient. The simulation signals obtained by the finite element simulation software of ABAQUS and the measured signals of the guided wave were decomposed sparsely by using a matching pursuit algorithm based on Gabor dictionary respectively, then the phase characteristic of the echo signals were verified by the phase parameters of matching atoms. The measured signals were collected by detecting identify buried and free guardrail posts usingT(0, 1) mode guided wave with the frequency of 64 kHz and 128 kHz, respectively. The experimental results of the simulated and measured signals are in good agreement with those of the theoretical analysis. The phase characteristic analysis of the echo signal provides a new way to the signal processing in guided wave detections.

ultrasonic guided-wave technology; phase characteristic; matching pursuit; guardrail post; signal extraction

国家自然科学基金(61271084)；安徽科技学院科研启动项目(ZRC2014457)；安徽科技学院重点建设学科支持项目(AKZDXK2015C03); 安徽省科技攻关项目(1604a0902134); 安徽省教育厅自然科学重点项目(KJZ016A183)

2015-09-29 修改稿收到日期：2016-01-18

柳伟续 男，硕士，讲师，1987年生 E-mail:liuweixu6024687@126.com

U417.12

A

10.13465/j.cnki.jvs.2017.06.035