基于P-I模型的爆炸载荷下波纹板防爆墙抗爆能力评估

师吉浩， 朱 渊， 陈国明， 付建民， 刘少杰

(中国石油大学(华东) 海洋油气装备与安全技术研究中心，山东 青岛 266580)

基于P-I模型的爆炸载荷下波纹板防爆墙抗爆能力评估

师吉浩， 朱 渊， 陈国明， 付建民， 刘少杰

(中国石油大学(华东) 海洋油气装备与安全技术研究中心，山东 青岛 266580)

以非线性有限元分析方法为基础，分析三种波纹板防爆墙在不同爆炸载荷下的动态响应及破坏机理，基于最大破裂应变准则，采用P-I模型，拟合三种类型波纹板防爆墙的抗爆评估P-I曲线，获取确定拟合不同防爆墙P-I曲线的统一经验方程形式，借助方差分析，进行波纹板防爆墙P-I曲线的参数影响性分析，基于最小二乘法，建立任意截面尺寸波纹板防爆墙P-I曲线的预测经验公式，结合实际案例，预测某截面尺寸下波纹板防爆墙的抗爆能力，并与实验实测值、单自由度理论模型进行对比。预测经验公式由于考虑应变率效应及局部响应效应，更具有准确性，其可用于快速、便捷地进行油气爆炸载荷下任意截面尺寸防爆墙抗爆能力评估，为工程人员初始抗爆设计、灾后后果评估提供参考。

波纹板防爆墙；破坏机理；P-I模型；最小二乘法；预测经验经验公式；初始抗爆设计；后果评估

油气燃爆事故是海洋油气资源开发过程重大风险之一，占据海洋平台事故的70%[1-2]。作为海洋平台主动防护系统之一，波纹板防爆墙用于隔离工作人员及重要设备，使其免受工艺受限区油气爆炸载荷影响。然而研究表明，现役波纹板防爆墙由于实际抗爆设计过程中低估爆炸载荷的影响，面临较大的失效风险[3-4]。1988年Piper Alpha平台发生法兰处可燃气体泄漏爆炸事故，由于油气工艺区域设备密集，爆炸超压响应剧烈，且由于低估可能造成的爆炸超压，平台上防爆墙没能起到有效减缓爆炸超压的作用，导致更多设备受损，发生二次爆炸，最终平台在大火中沉没；2010年“深水地平线”井喷燃爆载荷导致钻台上部波纹板舱壁严重破裂，由于失去这一关键屏障，舱内消防、电力等重要设备相继在爆炸和大火中失效，给救援减灾工作带来不便。

国内外规范[5-8]使用基于单自由度SDOF模型的简化方法，实现对波纹板防爆墙动态响应分析及抗爆设计。首先单自由度SDOF模型只考虑一种失效模式，当局部响应尤其是受挤翼缘屈曲影响塑性铰形成时，该模型就会不准确；其次，模型可能低估防爆墙各波纹板单元结构之间的相互作用，高估边界约束作用，同时使用弹性或理想弹塑性的阻抗函数，在评估爆炸载荷下防爆墙的塑性响应方面可能存在不足。

LOUCA等[9-10]致力于防爆墙抗爆评估以及影响因素分析，通过使用非线性有限元分析NLFEA(Nonlinear Finite Element Analysis)，以三种波纹板防爆墙为对象，讨论横截面压平、局部横向力效应、连接段旋转以及横截面拥挤效应对爆炸载荷下防爆墙整个响应过程的影响，据此提出一种基于性能的防爆墙设计方法。LANGDON等[11-14]提出并发展了一种由两个弹性次梁和五个弹簧组成新型简化梁模型体系，并推广到波纹板防爆墙，然而模型五个弹簧特性获取过程繁冗，且由于没有考虑到大变形下的应变硬化效应，模型在评估大塑性变形时存在缺陷。 KRAUTHAMMER等[15]推荐使用P-I模型对结构损伤进行评估，首先通过能量平衡法确定P-I曲线的超压渐近线和冲量渐近线，进而基于数值模拟计算，得到对应于临界损伤的P-I曲线。SOHN等[16]采用数值模拟方法获取爆炸载荷下FPSO上部模块防爆墙的P-I评估曲线，并与单自由度方法进行对比，得出数值模拟方法在评估复杂模型方面更精确。

考虑非线性有限元方法在评估波纹板防爆墙动态响应方面更准确、可靠，本文采用此方法，获取任意截面尺寸波纹板防爆墙抗爆评估P-I曲线的预测经验公式。首先，建立海洋平台典型防爆墙数值模型，结合实验验证，基于最大破裂应变准则，分析防爆墙在爆炸载荷作用下的动态响应及破坏模式，获取拟合不同防爆墙P-I曲线的统一经验方程形式；其次，由方差分析，确定不同截面参数对P-I曲线影响的显著性；最终构建任意截面尺寸下的波纹板防爆墙P-I曲线的预测经验公式，预测某种截面尺寸波纹板防爆墙的抗爆能力，通过与实验模型、单自由度模型进行对比，验证经验公式的准确性。预测经验公式可实现简捷、准确地评估任意截面尺寸波纹板防爆墙抗爆能力，为工程人员在防爆墙初始截面设计、灾后后果评估阶段开展相关工作提供参考。

1 爆炸载荷下波纹板防爆墙数值模型及验证

海洋平台防爆墙一般具有较长的横向距离，通过建立复杂模型对防爆墙进行数值损伤评估过程非常繁琐，研究发现，将其简化成三个槽型剖面结构可以准确的描述其抗爆性能[17]。以文献[17]提出的三种海洋平台波纹板防爆墙为研究对象，简化爆炸三角载荷，建立数值模型，并结合实验对比，验证模型的准确性。

1.1 海洋平台波纹板防爆墙数值模型

三种波纹板防爆墙如图1所示，参数见表1，防爆墙由波纹板及末端连接的两个底板组成，分别定义为S1(深槽型)、S2(中型槽)、S3(浅槽型)，槽型参数见文献[17]，为尽可能减少底板扭曲对槽型板动态响应的影响，底板厚度分别为20 mm、20 mm、6 mm[17]。

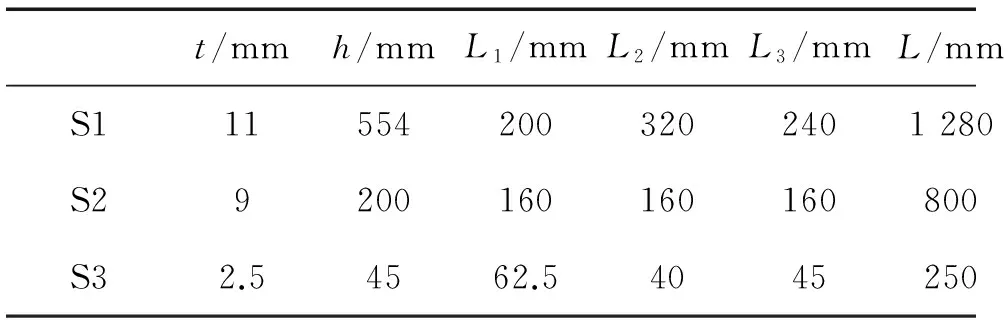
表1 三种防爆墙槽型参数Tab.1 Profiled parametersof three typical blast wallst/mm

根据海洋平台防爆墙的典型约束形式，设置波纹板末端为考虑面内约束的约束条件；两侧端面为对称约束条件，以代表防爆墙横向的连续性[17]。为既能保证数值模拟的准确性，又能节省计算时间，数值模拟需要合理的网格，根据前人研究经验[17]，将S1单槽划分网格数为8 000，S2、S3分别为4 000、3 000。

SS316钢材因具有较好的爆炸能消散能力、可有效防止突然失稳、保证防爆墙完整性等优点，而被广泛使用。数值模型采用SS316钢材，钢材采用Cowper-Symonds本构模型，考虑钢的应变率效应，具体参数见文献[18]。材料失效模型采用最大破裂应变准则[18]，合理准确的预测爆炸载荷下波纹板防爆墙的破坏模式，模型如下所示。

∑ εp1≥εcrit

(1)

式中，εpl为单元等效应变；εcrit为最大破裂失效应变，为0.25[18]。根据公式，当εpl大于0.25时，波纹板发生破裂。

图1 海洋平台典型防爆墙数值模型Fig.1 Numerical model of typical corrugated blast walls on the platform

1.2 波纹板防爆墙数值模型验证

为验证数值模型的准确性，以两端具有短型支撑转角的半片波纹板为对象，建立数值模型，获取超压分别为91 kPa、192 kPa的计算结果，并与实验值进行对比[11-13]。半片波纹板防爆墙数值模型如图2所示，波纹板上、下两端通过两个焊接转角，连接在固定约束的工字钢上，左右两端设置对称约束条件。模型采用shell单元，网格划分为4 mm，具体尺寸、材料参数见文献[11-13]。

图2 数值模型验证Fig.2 Verification of numerical model

在波纹板表面施加简化三角载荷，结果如图2(a)，超压峰值为92 kPa时，中部位移时程曲线与实验所测曲线一致，且中部最大位移为7.7 mm，相比实验值7.5 mm，误差小于5%，满足工程需求。图2(b)为超压峰值为192 kPa时，防爆墙的变形形状，可见波纹板底部翼缘、腹板发生屈曲变形，支撑转角张开并在与工字钢连接处形成塑性绞线，其与实验值(图2(c))具有良好的符合度，验证了数值模拟的准确性。

2 波纹板防爆墙抗爆P-I评估曲线统一经验方程形式

参考API规范[19]破裂指标，基于最大破裂应变准则，分析防爆墙的破坏模式，并获取拟合P-I曲线的统一经验方程形式。

2.1 爆炸载荷下波纹板防爆墙破坏模式

图3 S1防爆墙破坏模式Fig.3 Damage mechanism of S1

波纹板防爆墙在不同的爆炸载荷下可能发生不同的破坏模式，以S1型防爆墙为例进行分析。图3为S1型防爆墙在不同爆炸载荷作用下的三种破坏模式，如图3(a)所示，由于冲量载荷(超压P=2 000 kPa，I=8 500 kPa·ms)峰值超压大，作用时间短，在载荷作用初期，防爆墙腹板表面产生较大侧向惯性力，同时顶部翼缘表面产生较大的惯性压扁力，在两者共同作用下，腹板发生严重塑性屈曲变形。此时，防爆墙顶、底部翼缘由于受到腹板的支撑作用，其两侧约束端弯矩较小。由于冲量载荷作用时间远小于防爆墙固有振动周期，较短载荷作用下，防爆墙顶部、底部翼缘弯矩及弯曲变形尚未发展，顶部翼缘两侧约束端一定距离处，剪切力已经受惯性力影响迅速增加，且应变首先达到0.25，发生剪切破裂。

如图3(b)所示，动力载荷下(超压P=600 kPa，I=9 000 kPa·ms)，峰值超压减小，载荷作用时间接近防爆墙固有周期，在其作用下，防爆墙截面剪切力发展缓慢。然而在顶部翼缘压扁力与约束端轴向力作用下，顶部翼缘两侧约束端产生较大弯矩及拉力并发生屈服，应变达到0.25，发生拉伸破裂。如图3(c)所示，准静态载荷作用下(超压P=450 kPa，I=40 000 kPa·ms)，翼缘两侧约束端的破坏模式与动力载荷一致，发生拉伸破裂。然而，准静态载荷超压作用时间远大于防爆墙固有周期，由于受载荷作用时间较长，防爆墙顶部翼缘中心区域在发生弯曲变形过程中，产生较大局部横向力作用，并伴随褶皱线的形成，由于褶皱线附近的抗弯矩能力明显下降，中心区域最终在局部横向力作用下发生屈曲破裂。

综上，在冲量载荷下，S1型防爆墙在顶部翼缘两侧约束端一定距离处易发生剪切破坏，动力载荷下两侧约束端易发生拉伸破裂，随着爆炸载荷作用时间不断增加，在准静态载荷下，防爆墙顶部翼缘中心区域在局部横向力作用下，发生屈曲破裂。结合所有结果，S2型防爆墙在冲量载荷、动力载荷及准静态载荷下，约束端处分别发生剪切破裂、拉伸破裂及拉伸破裂；S3型防爆墙在冲量载荷下的破坏模式与S1类似，动力载荷及准静态载荷下的破坏模式与S2一致。

2.2 波纹板防爆墙P-I评估曲线方程

由破坏模式，使用最小二乘法，结合文献[20]，拟合S1、S2及S3型防爆墙P-I曲线，见图4，并建立如下形式的P-I经验方程式：

(P-P0)(I-I0)=A(P0/2+I0/2)β

(2)式中：P0为压力渐近线值，kPa，I0为冲量渐近线值，kPa·ms；A,β为常数，其值与防爆墙材料特性及截面属性有关；三种类型防爆墙P-I方程参数值如表2所示，A、β受防爆墙厚度影响很小，为了降低参数个数，A、β分别取常数5、1.35，经验方程式可以表达为统一形式：

(P-P0)(I-I0)=5(P0/2+I0/2)1.35

(3)

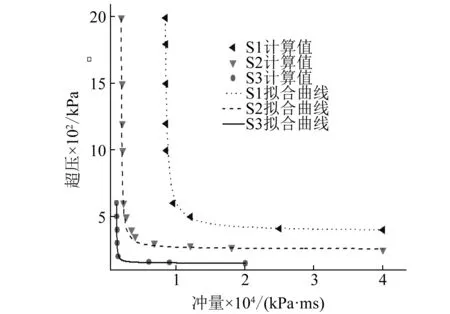
图4 三类防爆墙P-I曲线Fig.4 P-I curves of three typical blast walls

槽型P0I0AβS1390840051.35S2250190051.45S315012004.51.28

图5为式(2)所得P-I曲线与计算值比较，如图5所示，统一形式的方程拟合的曲线与计算数值相关性较好，说明经验公式可作为拟合波纹板防爆墙抗爆评估P-I曲线的统一方程形式。通过式(2)及其对应的曲线还可以得出，冲量渐近线值P0、压力渐近线值I0不同，防爆墙抗爆能力也不同。上述分析中，受波纹板截面参数的影响，S1型防爆墙冲量渐近线值P0、压力渐近线值I0较大，可承受较大的爆炸载荷。相比于S1，S2、S3型防爆墙由于截面参数较小，对应的渐近线值也随之减小，可承受爆炸载荷依次降低，说明防爆墙截面参数可能通过影响P-I曲线的冲量渐近线值P0、压力渐进线值I0大小，影响防爆墙的抗爆能力。

图5 统一方程式拟合P-I曲线与计算值比较Fig.5 Comparison between the general empirical equation with the simulations

3 波纹板防爆墙抗爆P-I评估曲线参数影响性分析

由2.2节，使用经验方程式(2)，拟合不同截面参数下防爆墙P-I曲线，并借助方差分析，获取截面参数对曲线影响的显著性情况。其中考虑的截面尺寸范围涵盖三种类型防爆墙所用参数，并在此基础上进行适当扩展，波纹板防爆墙厚度t为2.5～13 mm、底部翼缘宽度L1为60～240 mm、腹板宽度L2为40～400 mm、顶部翼缘宽度L3为40～320 mm、槽深度h为50～700 mm。

3.1 厚度t影响性分析

为验证统一经验方程式(2)在拟合任意截面参数防爆墙损伤评估P-I曲线的适用性，由方程拟合其他截面参数一定时，不同厚度下的防爆墙抗爆P-I评估曲线。取厚度t分别为2.5 mm，9 mm，11 mm及13 mm为例进行分析，如图6所示，P-I曲线与仿真计算值具有较好的相关性。表3为P-I曲线对应的超压渐近线P0、冲量渐近线I0，如表可得，随着厚度增加，压力和冲量渐近线值均增加，这可能由于在准静态载荷作用下，随着板厚度的增加，防爆墙抗弯刚度增大，两侧约束端处更难发生拉伸破裂；在冲量载荷作用下，随着厚度增加，防爆墙质量增加，提升了惯性阻力，同时减小腹板屈曲程度，从而提高了抗剪能力。由此说明，防爆墙厚度是影响波纹板板抗爆能力的因素之一，提升槽型板厚度可有效提高其抗爆性能。

图6 不同厚度P-I曲线Fig.6 P-I curves of different thickness

tP0I0134609700113908400934070002.51701300

3.2 底部翼缘宽度L1影响性分析

为研究波纹板防爆墙底部翼缘宽度L1对其P-I评估曲线及对应超压渐近线值、冲量渐近线值的影响，基于式(2)，拟合其他截面参数一定时，不同翼缘宽度L1波纹板防爆墙P-I评估曲线。取底部翼缘宽度L1分别为60 mm，160 mm，200 mm及240 mm进行分析，见表4。由表4可得，随着宽度L1增加，超压渐近线值、冲量渐近线值均减小，这可能是在准静态载荷下，虽然宽度增大、截面面积增大，其抗弯刚度也随之增加，但是由于面积的增大导致作用于底部翼缘上的力也增大，连接段弯矩也随之增大，此时弯矩增大效应大于抗弯刚度，最终导致连接段应力较大，更易发生屈服并破裂；在冲量载荷下，虽然底部翼缘宽度增大，防爆墙质量增大，截面惯性矩、惯性阻力随之增大，但由于作用于底部翼缘的惯性力与作用于腹板惯性侧向力效果强于惯性阻力的增加，腹板发生更严重的屈曲变形，连接段更易发生剪切破坏。故减小底部翼缘宽度L1，可降低防爆墙损伤程度，提高防爆墙抵抗爆炸载荷的能力。

表4 不同底部翼缘下超压、冲量渐近线值Tab.4 Overpressure and impact asymptotes of different flange at the bottom

3.3 腹板宽度L2影响性分析

通过相同方法，获取其他截面参数一定时，不同腹板宽度L2波纹板防爆墙P-I评估曲线，并取腹板宽度L2分别为40 mm，160 mm，320 mm及400 mm进行分析。如表5所示，与L1类似，随着L2增大，超压渐近线值、冲量渐近线值均减小，这是因为准静态载荷下，其他参数不变时，随着腹板宽度增大，防爆墙抗弯模量、抗弯刚度增大，但腹板倾斜角减小，作用于腹板垂直向下的力的分量增大，且其作用效果大于抗弯刚度的增大效果，防爆墙连接段产生更大的弯矩及应力，最终更容易发生拉伸破裂；冲量载荷下，由于作用于腹板的侧向力效应大于腹板截面惯性矩、惯性阻力增大效应，腹板更容易发生屈曲破裂。故减小底部翼缘宽度L2，可减小防爆墙损伤程度，提高防爆墙抵抗爆炸载荷的能力。

表5 不同腹板宽度下超压、冲量渐近线值Tab.5 Overpressure and impact asymptotes of different webs

3.4 顶部翼缘宽度L3影响性分析

同上，取其他截面参数一定时，不同顶部翼缘宽度L3下波纹板防爆墙获取的P-I评估曲线渐近线值并以L3分别为4 mm，160 mm，240 mm及320 mm为例进行分析。如表6所示，与L1、L2相反，随着L3增大，超压渐近线值、冲量渐近线值均增大，这是由于准静态载荷下，其他参数不变时，随着顶部翼缘宽度增大，防爆墙抗弯刚度增大，作用于顶部翼缘作用力也增大，其连接段弯矩增大，但由于同时受到深槽腹板支撑作用，连接段弯矩增大作用小于抗弯刚度，进而更难发生拉伸破裂；冲量载荷作用下，同样是由于深槽腹板的支撑作用，顶部翼缘截面惯性矩、惯性阻力增大效应大于作用力效应，连接段更难发生剪切破坏。故增大顶部翼缘宽度L3，可减小防爆墙损伤程度，提高防爆墙抵抗爆炸载荷的能力。

表6 不同顶部翼缘下超压、冲量渐近线值Tab.6 Overpressure and impact asymptotes of different flanges at the top

3.5 槽深度h影响性分析

同上，以其他截面参数一定时，槽深度h分别为50 mm，200 mm，554 mm及700mm的波纹板防爆墙为代表，拟合P-I评估曲线，得到压力渐近线值、冲量渐近线值。如表7所示，随着槽深度增加，压力和冲量渐近线值均增加，这是因为，在准态载荷作用下，其他参数不变时，深度增加，腹板的截面面积增大，抗弯刚度也随之增大，同时由于腹板倾斜角增大，作用于腹板力的竖直、水平力分量发生改变，共同作用下，连接段弯矩减小，应力减小，更难发生拉伸破裂；在冲量载荷作用下，由于腹板质量增大，截面惯性矩及惯性阻力增大效果大于作用力的增大效果，从而不易发生剪切破裂。故增大波纹板截面深度h，可减小防爆墙损伤程度，提高防爆墙抵抗爆炸载荷的能力。

表7 不同槽深度下超压、冲量渐近线值Tab.7 Overpressure and impact asymptotes of different groove depth

3.6 截面参数影响性方差分析

为进一步获取截面参数对防爆墙抗爆能力影响的显著性情况，设计正交试验，以截面参数影响冲量渐进线I0值进行分析，如表8所示。

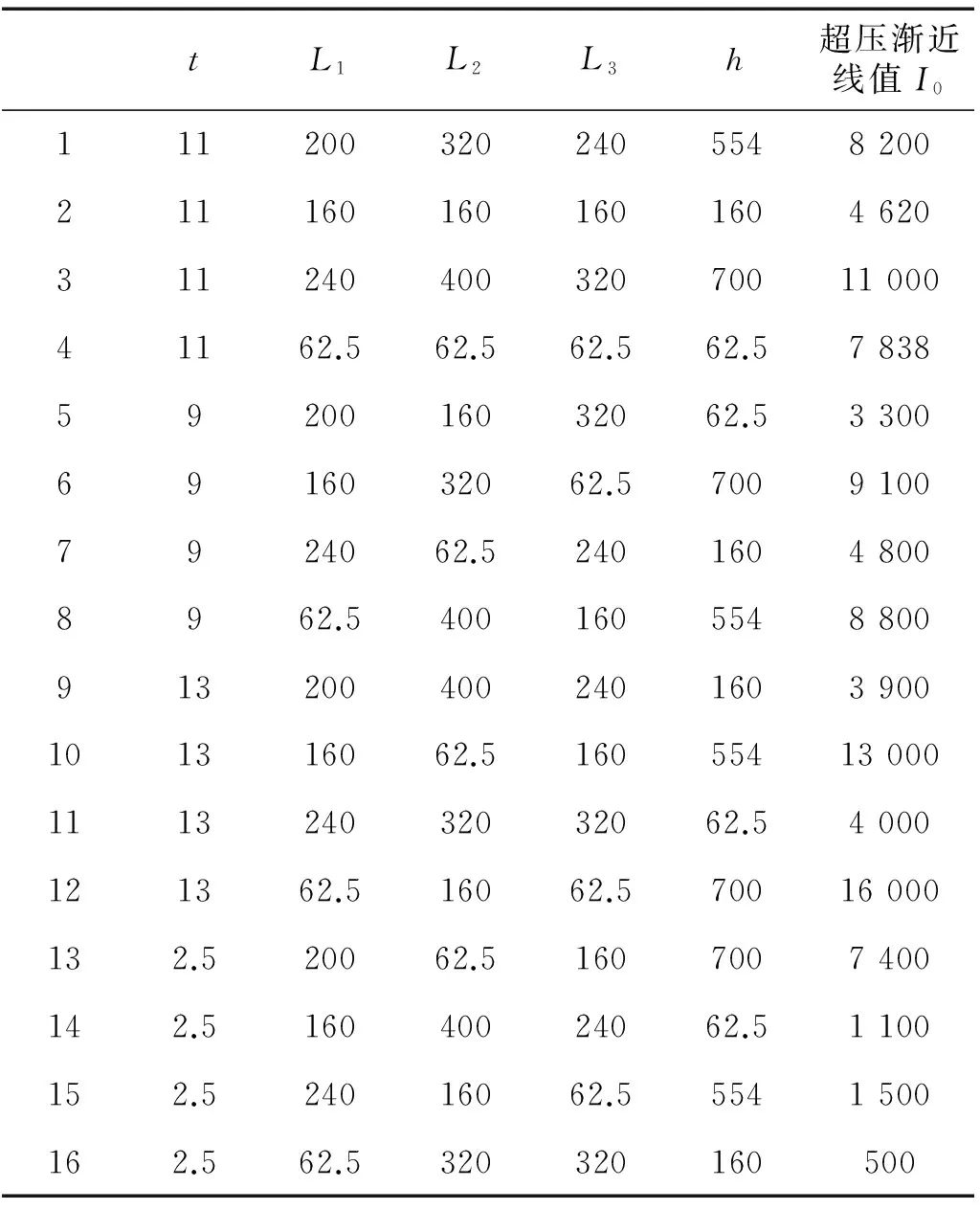
表8 正交试验设计Tab.8 Orthogonal test analysist

表9为方差分析结果，有表所示，截面参数中槽深度h、板厚度t对冲量渐进线值I0最为显著，其次为顶部翼缘宽度L3及底部翼缘宽度L1，两者相差不大且影响不显著，最小的为腹板宽度。截面参数对超压渐近线P0的影响与对冲量渐近线值I0一致，由于篇幅限制，不再赘述。故在进行防爆墙截面参数设计时，为提高防爆墙抗爆能力，可首先考虑槽深度及板厚度，其次也可减小顶部、底部翼缘宽度。

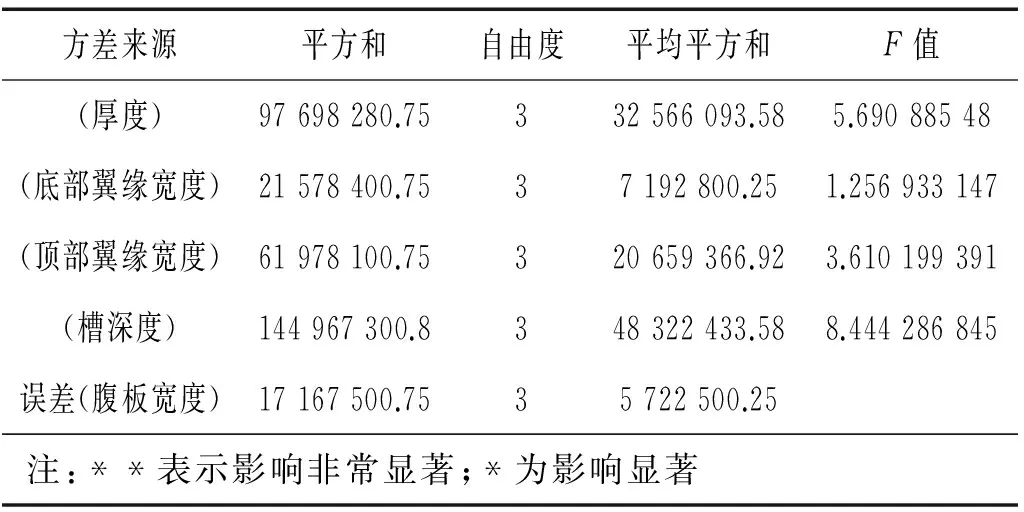
表9 方差分析结果Tab.9 Results of ANOVA

4 任意截面尺寸波纹板防爆墙抗爆P-I评估曲线预测经验公式及验证

由波纹板防爆墙P-I曲线的参数影响性分析结果，获取P-I曲线的预测经验公式，并与单自由度模型对比，验证经验公式的准确性。

4.1 P-I曲线的预测经验公式

基于最小二乘法，得到变量参数分别为L1、L2、L3、t、h，压力渐近线值P0与冲量渐近线值I0的预测经验公式，如下所示：

P0=413×et/22+203×e-L1/169+558×e-L2/672+35.76eL3/481+111×eh/430-1 171

(4)

I0=15 838×ln(t+12.5)-2 770×ln(L1+4.07)-2 199×ln(L2-0.76)+846×eL3/242+4 217×eh/603-27 539.5

(5)

由预测经验公式获取的压力渐近线值、冲量渐近线值与数值计算结果对比见表10、图7，由表10及图7可见，误差满足工程要求，说明预测经验公式在构建任意截面尺寸的P-I曲线方面具有较好适用性。

表10 数值结果与经验公式结果对比Tab.10 Comparison between the empirical equation with simulation results

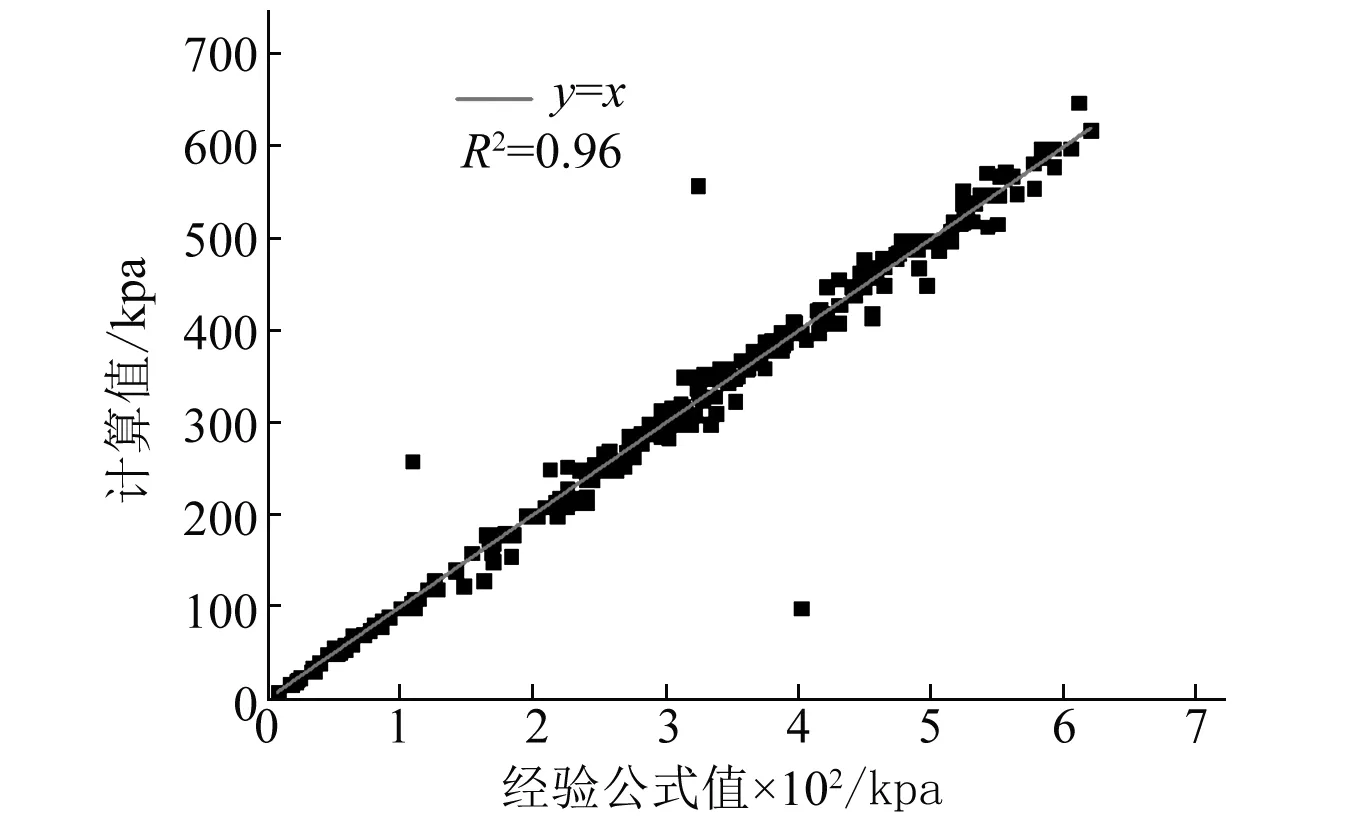
(a)超压渐近线值对比

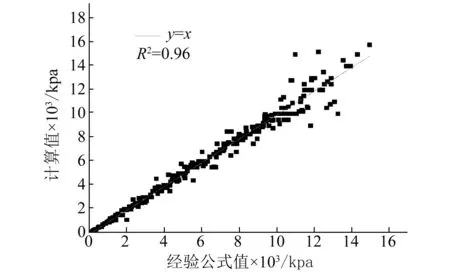
(b)冲量渐近线值对比图7 经验公式预测值与计算值相关性验证Fig.7 Correlation between the empirical equation and the simulations

4.2 经验公式与实验数据、单自由度模型对比

采用预测经验公式(4)、(5)及式(3)，预测某波纹板防爆墙抗爆P-I曲线，并与实验实测数据、单自由度理论模型进行对比，如图8所示。其中波纹板防爆墙截面参数厚度t为2.5 mm、底部翼缘宽度L1为62.5 mm、顶端翼缘宽度L2为45 mm、腹板宽度L3为45 mm、截面深度h为41 mm。

LOUCA等[20]对上述截面参数下的波纹板防爆墙进行了实验研究，其中在FFD23载荷下，防爆墙约束段发生破裂，而在FFD21与FFD39载荷下，防爆墙虽然发生塑性变形，但完整性保持良好。DNV推荐使用单自由度模型生成P-I曲线，对结构进行评估。模型将材料简化为理想弹塑性模型，以梁中部最大位移为指标，对爆炸载荷下结构动态响应过程及抗爆能力进行评估。模型将波纹板防爆墙转化成理想弹塑性梁体系，计算可得等效质量M为27.8 kg，等效刚度K为6.67×105N/m，取静准态载荷下防爆墙临界损伤弯曲位移180 mm为指标，获取单自由度P-I评估曲线。

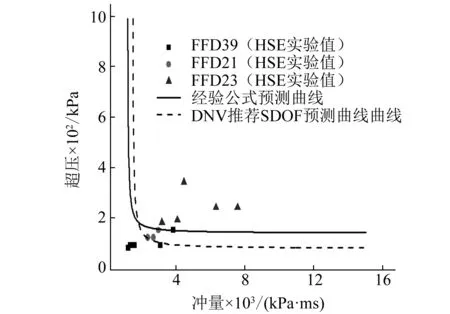
图8 预测曲线与计算值、单自由度对比Fig. 8 Comparison between the prediction curve and the simulations and the SDOF model

由图8，经验公式预测曲线能够准确预测上述截面尺寸防爆墙抗爆能力，曲线右侧表征防爆墙发生破裂，左侧为防爆墙完整性较好，未发生破裂，这与HSE所测三组实验值在图中的分布情况是一致的。而相比DNV推荐的SDOF理论曲线，经验公式所得超压渐近线值略大，这可能是由于SDOF方法采用理想弹塑性模型，忽略了材料应变率效应，低估了防爆墙的准静态载荷下的抗爆能力，这与SHI等[21-22]的研究一致，同时也进一步验证经验公式的准确性；在冲量载荷区间，经验公式预测冲量渐近线值小于单自由度预测模型，这可能是由于在冲量载荷下，应变率效应增加了防爆墙的抗爆能力，而局部响应如翼缘、腹板屈曲，却更易导致波纹板防爆墙发生剪切破坏，同时单自由度预测模型采用防爆墙临界损伤弯曲位移为指标，其往往大于剪切损伤临界的剪切位移，所以在冲量载荷下趋于剪切破坏模式时，单自由度模型可能过高评估其抗爆能力。故结合实测数据，相比单自由度预测模型，经验公式更准确地评估波纹板防爆墙抗爆能力。

5 结 论

(1) 由不同类型防爆墙爆炸载荷下破坏模式分析，探讨其破坏机理：冲量载荷下，惯性力效应导致S1型防爆墙在两侧约束端一定距离处发生剪切破坏；动力载荷下，弯矩效应导致约束端拉伸破裂；准静态载荷下，局部横向力导致顶部翼缘中心区域屈曲破裂；S2防爆墙在冲量载荷、动力载荷及准静态载荷下，分别发生剪切破裂、拉伸破裂及拉伸破裂；S3防爆墙在冲量载荷下的破坏模式与S1相似，其他载荷下与S2一致。

(2) 基于破坏模式，提出了获取波纹板防爆墙抗爆P-I评估曲线的方法，构建了P-I评估曲线统一方程形式，借助方差分析，获取参数影响显著性大小：其中槽深度、板厚度对防爆墙抗爆能力影响最为显著，增大槽深度、板厚度或减小顶部、底部翼缘宽度，均可提高防爆墙抗爆能力。

(3) 以参数影响性分析为基础，构建任意截面参数波纹板防爆墙抗爆P-I评估曲线预测经验公式，公式与实验实测数据保持一致，而相比单自由度模型，预测经验公式由于考虑应变率及局部响应效应，可实现更准确、便捷地评估波纹板防爆墙抗爆能力。

[ 1 ] HSE. Accident statistics for floating offshore unites on the UK continental shelf(1980—2003). HMSO RR 353[M]. London: Health and Safety Executive, 2005.

[ 2 ] PAIK J K, CZUJKO J, KIM B J, et al. Quantitative assessment of hydrocarbon explosion and fire risks in offshore installations[J]. Marine Structures, 2011, 24(2): 73-96.

[ 3 ] PAIK J K, CZUJKO J. Explosion and fire engineering of FPSOs (phase II): Definition of fire and gas explosion design loads[R]. Research Institute of Ship and Offshore Structural Design Innovation, Pusan National University, Busan, Korea, Final Report No. EFEF-03-R2, 2010.

[ 4 ] LOUCA L A, BOH J W. Analysis and design of profiled blast walls[M]. HSE Books, 2004.

[ 5 ] BIGGS J M, TESTA B. Introduction to structural dynamics[M]. New York: McGraw-Hill, 1964.

[ 6 ] Design against accidental loads :DNV-RP-C204. [S]. Norway: Det Norske Veritas, 2010.

[ 7 ] TOLLOCZKO J J A. Interim guidance notes for the design and protection of topside structures against explosion and fire[M]. Ascot, UK: Steel Construction Institute, 1992.

[ 8 ] BREWERTON R. Design guide for stainless steel blast wall-technical note 5[M]. London: Fire and Blast Information Group (FABIG), 1999.

[ 9 ] LOUCA L A, BOH J W, CHOO Y S. Design and analysis of stainless steel profiled blast barriers[J]. Journal of Constructional Steel Research, 2004, 60(12): 1699-1723.

[10] LOUCA L A, BOH J W, CHOO Y S. Response of profiled barriers subject to hydrocarbon explosions[J]. Proceedings of the ICE-Structures and Buildings, 2004, 157(5): 319-331.

[11] LANGDON G S , SCHLEYER G K. Inelastic deformation and failure of profiled stainless steel blast walls. Part Ⅰ: experimental investigations[J]. International Journal of Impact Engineering, 2005,31:341-369.

[12] LANGDON G S, SCHLEYER G K. Inelastic deformation and failure of profiled stainless steel blast walls. Part Ⅱ: analyticalmodeling considerations[J]. International Journal of Impact Engineering, 2005,31:371-399.

[13] LANGDON G S, SCHLEYER G K. Deformation and failure of profiled stainless steel blast wall panels. Part III: finite element simulations and overall summary[J]. International Journal of Impact Engineering, 2006, 32(6): 988-1012.

[14] LIANG Y H, LOUCA L A, HOBBS R E. Corrugated panels under dynamic loads[J]. International Journal of Impact Engineering, 2007, 34(7): 1185-1201.

[15] KRAUTHAMMER T, ASTARLIOGLU S, BLASKO J, et al. Pressure-impulse diagrams for the behavior assessment of structural components[J]. International Journal of Impact Engineering, 2008, 35(8): 771-783.

[16] SOHN J M, KIM S J, KIM B H, et al. Nonlinear structural consequence analysis of FPSO topside blastwalls[J]. Ocean Engineering, 2013, 60: 149-162.

[17] BOH J W, LOUCA L A, CHOO Y S. Numerical assessment of explosion resistant profiled barriers[J]. Marine structures, 2004, 17(2): 139-160.

[18] BOH J W, LOUCA L A, CHOO Y S. Strain rate effects on the response of stainless steel corrugated firewalls subjected to hydrocarbon explosions[J]. Journal of Constructional Steel Research, 2004, 60(1): 1-29.

[19] O’CONNOR P E, VERSOWSKY P E, BUCKNELL J R, et al. API RP2FB: Design of offshore facilities against fire and blast loading[C]//Offshore Technology Conference, 2005.

[20] LOUCA L A, FRIIS J. Modelling failure of welded connections to corrugated panel structures under blast loading[R]. OffshoreTechnology Report-Health and Safety Executive OTO, 2000.

[21] SHI Y, HAO H, LI Z X. Numerical derivation of pressure-impulse diagrams for prediction of RC column damage to blast loads[J]. International Journal of Impact Engineering, 2008, 35(11): 1213-1227.

[22] LAN S R, CRAWFORD J C. Evaluation of the blast resistance of metal deck proofs[C]//5th Asia-Pacific Conference on Shock & Impact Loads on Structures. Changsha, 2003.

Assessment of blast resistance capacities of corrugated blast walls based on the P-I Model

SHI Jihao， ZHU Yuan， CHEN Guoming， FU Jianmin， LIU Shaojie

(Center for Offshore Engineering and Safety Technology, China University of Petroleum, Qingdao 266580, China)

In view of the insufficient ability to assess the damage of corrugated blast walls subjected to blast loads by using the SDOF model, a NLFEA (nonlinear finite element analysis model was built to analyze the dynamic response and damage mechanism of three kinds of typical corrugated blast walls on a platform. P-I diagrams and a simplified empirical equation were both derived with the P-I model where the material rupture was defined as a critical indicator and the maximum rupture strain criterion was combinedly used. Using the simplified empirical equation, a study on the critical parameters of the equation, i.e. the critical values of the overpressure and the impact, was performed under different sizes of the sectional profiles of corrugated blast walls with the variance analysis method. Based on the least squares method, a general empirical equation under different sizes of the sectional profiles was derived, with which the prediction of the blast loading resistance of a new corrugated blast wall was made. In comparison with the SDOF model, the results by the general empirical equation have better correlation with those by the simulations. It is concluded the empirical equation is of convenience and accuracy to assess the damage of corrugated blast walls and can provide a guidance to the initial design and consequence assessment of corrugated blast walls.

corrugated blast walls; damage mechanism; P-I model; least squares method; empirical equation; initial explosion-roof design; consequence assessment

国家自然科学基金；中央高校基本科研业务费专项资金项目(15CX05018A)

2015-10-19 修改稿收到日期：2016-01-20

师吉浩 男， 博士生， 1990年生

朱渊 男， 副教授， 1982年生

TU352.1

A

10.13465/j.cnki.jvs.2017.06.029