一种球面网壳动力失效的联合预测方法
2017-04-11黄艳霞周广春于德广
张 明, 张 瑀, 黄艳霞, 周广春, 于德广
(1. 西南交通大学 土木工程学院 成都 610031;2.结构工程灾变与控制教育部生点实验室(哈尔滨工业大学),哈尔滨 150090;3.哈尔滨工业大学 土木工程学院,哈尔滨 150090;4.中国恩菲工程技术有限公司,北京 100038)
一种球面网壳动力失效的联合预测方法
张明1, 张瑀2,3, 黄艳霞1, 周广春2,3, 于德广4
(1. 西南交通大学 土木工程学院成都610031;2.结构工程灾变与控制教育部生点实验室(哈尔滨工业大学),哈尔滨150090;3.哈尔滨工业大学土木工程学院,哈尔滨150090;4.中国恩菲工程技术有限公司,北京100038)
以地震作用下精细化有限元分析的单层球面网壳的动力失稳破坏模式为基础、结合细胞自动机(CA)方法,发展了一套单层网壳动力失稳破坏模式和失效荷载的联合预测方法。首先,对基础单层球面网壳进行了简谐荷载作用下全荷载域动力时程有限元分析(FEA),并时时提取各级动荷载幅值下所有节点的位移值及单元的应变能密度。之后,用建立的联合方法预测了其它同类网壳的动力失稳破坏模式及失效荷载,并与相应FEA 计算结果进行了分析比较。结果表明,所提出的联合方法,在一定程度上能基于一个单层球面网壳的动力失稳破坏模式和失效荷载预测其它不同跨度、不同矢跨比、不同杆件截面尺寸的单层球面网壳的动力失稳破坏模式及失效荷载。因此,结合FEA数值模拟,实现了CA方法在单层球面网壳动力失稳破坏模式和失效荷载预测中的应用。
联合预测方法;单层球面网壳;简谐地面运动;动力失稳破坏模式;动力失效荷载
单层网壳结构在强震作用下的动力工作性能具有很强的随机性,破坏机理十分复杂[1]。因此,国内外学者对网壳结构在地震作用下的失效机理和动力失稳破坏模式[2-6]等进行了深入研究,为网壳结构工程设计提供了重要依据。
目前,对单层网壳动力失效机理的研究遇到两个问题:①单层网壳多是高次超静定结构,加之地震作用的随机性,故导致其失效机理复杂,失效模式和失效荷载预测难度大;②实验费用大、周期长及缩尺模型实验难反映实际单层网壳的动力工作特性。因此,难以通过实验研究单层网壳结构的动力失效机理。进而,对于单层网壳结构动力失效机理的研究一般基于有限元程序的全荷载域动力时程分析进行:根据计算出的结构最大节点位移、塑性杆件比例、以及结构刚度的变化情况等指标判别其破坏形式[7-9]。但有限元数值模拟需要反复试算,计算量很大,后处理时间长。
鉴于上述问题,作者借鉴ZHOU等[10-16]发展的结构人工智能分析方法,开发了一套基于细胞自动机(CA)和有限元分析(FEA)相结构的联合方法,对拟建同类单层网壳结构进行快捷且不失有限元分析精度的动力失稳破坏模式及失效荷载进行预测。该联合方法既开拓了既有FEA数值模拟结果的应用,又借鉴了智能技术在结构分析领域的最新研究成果,形成了传统数值模拟方法与人工智能方法相结合的联合预测方法。
1 单层球面网壳失效模式预测
[17],基于CA方法预测单层球面网壳动力失稳破坏模式的原理如下:
1)节点(细胞元)状态值的计算
单层球面网壳结构节点(细胞元)状态值的计算方法如式(1)所示:
(1)
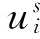
2)相似节点域匹配准则
单层球面网壳结构相似节点域的匹配准则如式(2)所示:

(2)

3)破坏模式投射准则
目标单层球面网壳中节点i归一化位移值由公式(3)给出:
(3)

当目标单层球面网壳所有节点得到基础网壳的投射值后,就得到了目标单层球面网壳动力失稳时的破坏模式。

(4)
通过式(4)可对目标单层球面网壳动力失稳破坏模式的预测精度进行度量。
在上述理论基础上,单层网壳动力失稳破坏模式的预测流程,如图1所示。
1)建立数据库:本文主要基于FEA所得到的单层球面网壳结构动力失效模式建立数据库。该数据库主要包括基础网壳和目标网壳的动力失稳破坏模式及相应的失效荷载。
2)建立CA数值模式:应用式(1)建立不同地震作用下的CA数值模式。
3)建立匹配准则:本文采用式(2)建立基础网壳与目标网壳之间的相似节点域匹配准则。
4)相似节点域的确定:应用匹配准则在基础网壳与目标网壳的CA数值模式之间确定相似节点域。
5)目标网壳破坏模式的确定:该联合方法认为基于CA数值模式和匹配准则所找到的基础网壳与目标网壳的相似节点域,破坏时具有相同的破坏模式。依据该思想及基础网壳的破坏模式、采用式(3)可以匹配出目标网壳失效时的节点位移模式。

图1 单层球面网壳动力失稳破坏模式的联合预测方法Fig.1 The combined method for mapping the dynamicinstability mode of single-layer latticed dome
基于上述联合预测方法,下面将给出应用联合方法预测出的单层球面网壳动力失稳破坏模式的算例,以检验该方法的有效性。
1.1单层球面网壳数值模拟
单层球面网壳的结构形式为工程中常见的凯威特型(K8),见图2,其跨度为L,矢高为f。截面尺寸满足常规静力设计要求,其中主肋杆和环杆截面尺寸较大,斜杆截面尺寸较小,考虑结构初始缺陷的影响。
假定网壳模型的节点均为刚性连接,周边为三向固定铰支;屋面质量按壳体表面积计算,转化为集中质量凝聚在节点处;杆件选用Pipe20单元,节点采用Mass21单元;材料为双线型随动强化模型,割线模量Et等于0.02倍的弹性模量E,屈服点235 MPa;采用Rayleigh阻尼,阻尼比为 0.02。

图2 K8型网壳模型示意图Fig.2 The single-layer latticed dome K8
1.2失效模式预测算例
以FEA方法得到的数据为基础,应用联合方法对单层球面网壳动力失稳破坏模式的预测结果列于表1中。表中分成四种工况对联合方法预测效果进行了讨论,即不同简谐波作用下及不同矢跨比、跨度和杆件截面尺寸不同的网壳之间动力失稳破坏模式预测。
从表1可以看出联合方法所预测的失效模式与目标网壳的动力失稳破坏模式:最大位移区域是基本一致的;平均相似度在80%以上。进一步对表1预测结果进行分析可知:
1)该方法适用于塑性发展程度较浅的单层网壳结构的动力失稳破坏模式预测。对于塑性发展程度较深的失稳破坏模式,该方法的预测精度较差,如网壳D40207的失稳破坏模的相似度仅有75.62%。
2)数据库中的样本越大,该方法预测网壳结构的失稳破坏的精度越高。例如,跨度较大的网壳节点多,其基础数据便多,据其预测跨度较小网壳失稳破坏模式的精度就略高。
3)基础网壳与目标网壳构造越接近,该联合方法预测的失稳破坏模式精度就越高。例如,网壳D40203a与D40203c的基频较为疏远,网壳D60203a与D60203b的基频较为接近,后者的预测精度却较高。
据上述分析可知,该联合方法能够初步实现单层球面网壳动力失稳破坏模式的预测,可以为单层网壳结构工程设计提供参考。
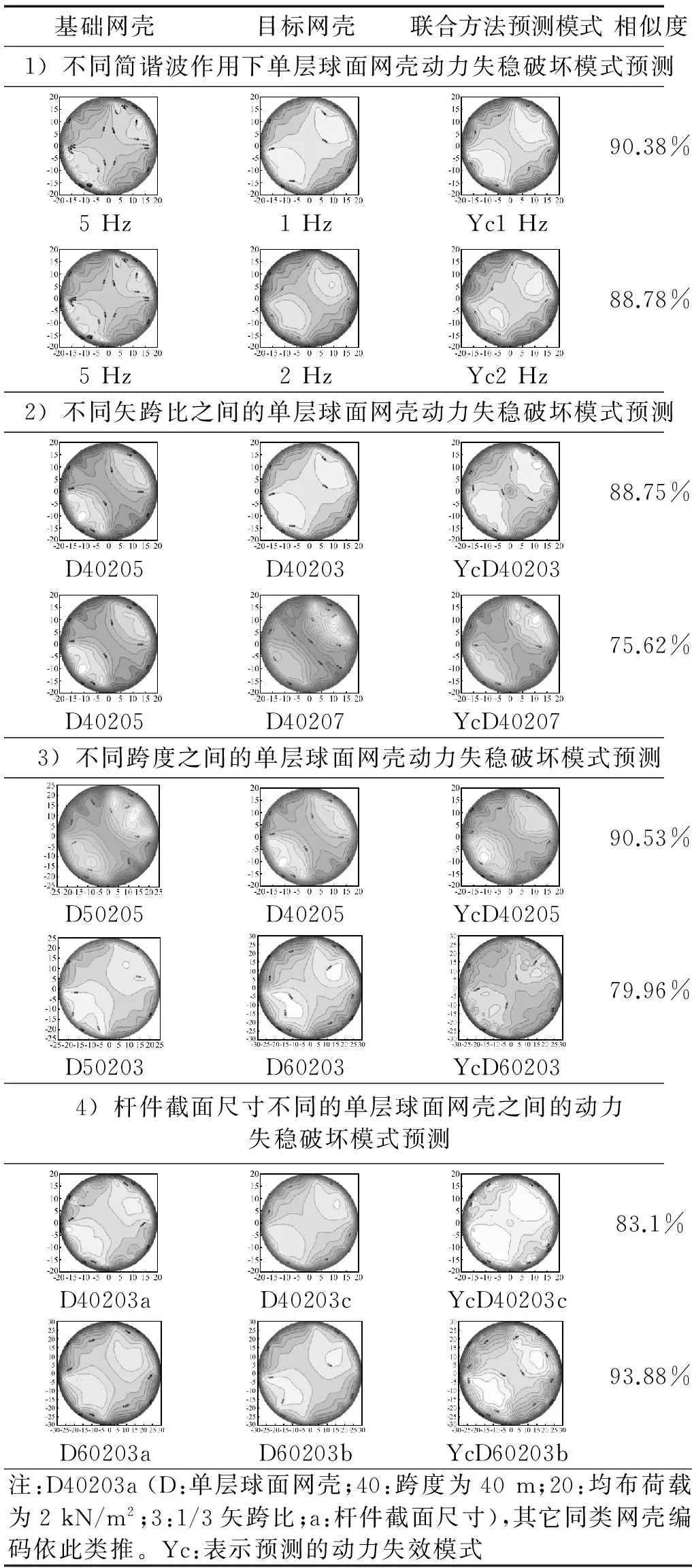
表1 联合方法与FEA方法得到的网壳失稳破坏模式比较Tab.1. The comparison of the combined and FEA methods
2 单层球面网壳失荷载预测
2.1预测结构失效荷载的联合方法简介
文献[18]指出外界对结构的输入能量小于等于结构极限耗能时,结构处于正常工作状态。同时,文献[19]也指出结构失效时,结构指数应变能密度和值与加速度峰值曲线将发生突变。在此基础上,本文认为单层球面网壳结构体系遵循着相同的失效规则,有着相同的极限耗能能力。但结构失效时,应变能分量要远远大于动能和阻尼耗能。基于此,本文初步给出结构失效荷载的预测公式。
[W] =FD
(5)
式中:[W]为结构体系的极限耗能;F为作用于结构体系的外荷载;D为在外荷载作用下结构体系的位移。
进一步,式(5)可以表述为:
[W] =kAId
(6)
式中:k=k1k2;A为加速度峰值;Id为失效荷载作用下结构的指数应变能密度和值[19];k1A对应于式(5)中的F,k1为A与F的转换系数;而k2Id对应于D,k2为Id与D的转换系数。
对于基础网壳和目标网壳而言,其相应计算式分别为式(7)和(8):
[W] =kAbaseIdbase
(7)
[W] =kAobjIdobj
(8)
式中:Abase为基础网壳失效时所对应的加速度峰值;Idbase为失效荷载作用下基础网壳所对应的指数应变能密度和值;Aobj为目标网壳失效时所对应的加速度峰值;Idobj为失效荷载作用下目标网壳所对应的指数应变能密度和值。特别注意,Idobj基于指数应变能密度分布模式,寻找到基础网壳与目标网壳相似区域后,通过投射准则得到,其详细计算流程见图2。
进而,我们可以得到式(9)
(9)
基于式(9),可以建立相应的联合方法对网壳失效荷载进行预测。
预测网壳结构失效荷载的联合方法如图3所示。

图3 预测网壳结构失效荷载的联合方法Fig. 3 The combined method for predicting thefailure load of the object shell
其步骤可简述为:①通过全荷载域动力时程分析得到基础网壳和目标网壳在单位荷载峰值的地震动作用下节点域指数应变能密度数模式、失效荷载及相应的节点域指数应变能密度数模式;②根据匹配准则,找出基础网壳和目标网壳间的相似节点域;③结构失效时,基于投射准则将基础网壳上与目标网壳相似的节点指数应变能密度值投射到目标网壳的相应节点上,得到目标网壳的节点域指数应变能密度失效模式;④按照式(9)计算得到目标网壳的失效荷载。
2.2误差分析
为了考察联合方法预测网壳结构失效荷载的准确性,本文将预测结果与有限元分析结果按照式(10)进行比较:
(10)
式中,Aobj和AFEA分别为目标网壳失效荷载预测值和有限元计算结果。
2.3失效荷载预测算例
以单层球面网壳遭遇简谐荷载作用下的失效荷载预测为例,对联合方法预测网壳结构失效荷载的合理性进行检验,见表2。
首先,以频率为3.2Hz简谐地面运动作用下D40203a的FEA模拟数据为基础,对频率为1Hz简谐荷载作用下D40203的失效荷载进行预测,预测结果列于表2中第1组别;之后,根据杆件截面尺寸不同,分别以D50203b和D60203b为基础网壳对目标网壳D50203d和D60203d的失效荷载进行预测,分别列于表2中第2和3组别;根据矢跨比不同,分别以D40203a和D40205a为基础网壳对目标网壳D40205a和D40207a的失效荷载进行预测,分别列于表2中第4和5组别;根据跨度不同,分别以D60205和D40203a为基础网壳对目标网壳D40203a、D50207和D50205的失效荷载进行预测,分别列于第6~8组别。表2中同时还给出了相应于不同组别的目标网壳的失效荷载及误差。
分析表2可知,基于联合方法预测单层球面网壳失效荷载的误差基本都控制在20%以内,说明可以应用该方法对单层球面网壳的失效荷载进行预测。同时,表中也有个别组别的误差较大,如第1组别和第6组别等,其可能是由有限元计算的失效荷载、失效模式与真实的失效荷载及失效模式差距较大引起。
上述算例表明,可以应用联合方法基于某一网壳结构失效时所对应的简谐地面运动的幅值和频率预测其他不同构造网壳结构的失效荷载。另外,文献[20]研究表明:地震动持续时间对结构的弹性反应或进入塑性程度不深的弹塑性反应没影响或基本上没影响。事实上,简谐地面运动作用下单层网壳结构多发生动力失稳破坏,塑性发展程度一般较浅。因此,本文暂时没有考虑地震动持时对结构失效荷载的影响。

表2 简谐荷载作用下单层球面网壳失效荷载的预测Tab. 2 Failure load prediction of the single-layer spherical reticulated shells subjected to harmonic load
3 结 论
本文的主要贡献是结合细胞自动机技术和传统有限元分析方法建立了一套单层球面网壳结构失效模式和失效荷载的联合预测方法。从预测精度上来看,该方法预测的结果可以为工程分析提供参考;从计算效率来看,该方法相比较于传统有限分析方法可以节省大量的计算时间及计算机存储空间。同时,也应该注意到无论是全荷载域动力时程有限元分析方法还是本文提出的联合预测方法都缺少实验验证,故下一步重点研究的方向,将是开发网壳模型振动台的实验研究。
致谢
感谢西南交通大学和哈尔滨工业大学“空间结构研究中心”为本课题研究所提供的技术支持!
参 考 文 献
[ 1 ] 刘文政, 罗永峰. 单层球面网壳基于节点构形度的刚度均匀性判定准则[J]. 建筑结构学报, 2015, 36(11): 38-45. LIU Wenzheng, LUO Yongfeng. Uniform stiffness criterion of single-layer spherical shells based on nodal well-formedness [J]. Journal of Building Structures, 2015, 36(11): 38-45.
[ 2 ] YAMADA S. Vibration behaviour of single-layer latticed cylindrical roofs [J]. International Journal of Space Structures. 1997 (3/4):181-190.
[ 3 ] KUMAGAI T, OGAWA T. Dynamic buckling behavior of single layer latticed domes subjected to horizontal step wave[J]. Journal of the International Association for Shell and Spatial Structures, 2003, 44(3): 167-174.
[ 4 ] FAN F, WANG D Z, ZHI X D, et al. Failure modes of reticulated domes subjected to impact and the judgment [J]. Thin-Walled Structures, 2010, 48(2): 143-149.
[ 5 ] FAN F, WANG D Z, ZHI X D, et al. Failure mechanism for single-layer reticulated dome under impact loads based on microcosmic dynamic response [C]∥ Materials and Structures. Hangzhou, 2008: 155-164.
[ 6 ] 韦征,叶继红,沈世钊.基于最大熵法的单层球面网壳在地震作用下的破坏模式预测[J]. 振动与冲击, 2008, 27(6):64-69. WEI Zheng, YE Jihong, SHEN Shizhao. Failure type prediction of single-layer spherical shells under earthquake excitation based on maximum entropy [J]. Journal of Vibration and Shock, 2008, 27(6): 64-69.
[ 7 ] 沈世钊, 支旭东. 球面网壳结构在强震下的失效机理[J].土木工程学报, 2005, 38(1):11-20. SHEN Shizhao, ZHI Xudong. Failure mechanism of reticular shells subjected to dynamic actions [J]. China Civil Engineering Journal, 2005, 38(1):11-20.
[ 8 ] 苑宏宇. 单层球面网壳的最不利动荷载分析和动力失效分析[D]. 南京:东南大学, 2006.
[ 9 ] 苑宏宇, 叶继红, 沈世钊, 等. 单层球面网壳在简单动荷载作用下的失效研究[J]. 工程抗震与加固改造, 2006, 28(4):10-17. YUAN Hongyu, YE Jihong, SHEN Shizhao, et al. Failure mechanism analysis of single-layer spherical shells subjected to simple dynamic loads [J]. Earthquake Resistant Engineering and Retrofitting, 2006, 28(4):10-17.
[10] ZHOU G C. Application of stiffness/strength corrector and cellular automata in predicting response of laterally loaded masonry panels [D]. Plymouth: University of Plymouth, 2002.
[11] SARKAR P. A brief history of cellular automata [J]. ACM Comput Surv, 2000, 32(1): 80-107.
[12] ZHOU G C, RAFIQ M Y, BUGMANN G, et al. Cellular automata model for predicting the failure pattern of laterally loaded masonry panels [J]. Journal of Computing in Civil Engineering, 2006, 20(6): 400-409.
[13] PAN D, ZHOU G C, RAFIQ M Y. An artificial neural network model for predicting failure load of masonry wall panel under lateral load [C]∥ Intelligent Computing in Engineering. Plymouth, UK, 2008: 451-459.
[14] ZHANG Y, ZHOU G C, XIONG Y, et al. Techniques for predicting cracking pattern of masonry wallet using artificial neural networks and cellular automata [J]. Journal of Computing in Civil Engineering, 2010, 24(2): 161-172.
[15] 杨书仪,刘德顺,赵继云. 储液容器跌冲落动力学神经网络建模[J]. 计算力学学报, 2010. 27(3):442-445. YANG Shuyi, LIU Deshun, ZHAO Jiyun. Neural network modeling for the drop impact dynamics of fluid-filled container [J]. Chinese Journal of Computational Mechanics, 2010, 27(3):442-445.
[16] 李刚, 刘志强. 基于支持向量机替代模型的可靠性分析[J]. 计算力学学报, 2011, 28(5): 676-681. LI Gang, LIU Zhiqiang. Surrogate-based reliability analysis by support vector machine [J]. Chinese Journal of Computational Mechanics, 2011, 28(5):676-681.
[17] 张明, 张瑀, 景志涛, 等. 预测单层柱面网壳破坏模式的细胞自动机方法[J]. 哈尔滨工业大学学报, 2013, 45(2): 14-19. ZHANG Ming, ZHANG Yu, JING Zhitao, et al. Cellular autuomata technique for predicting failure mode of single-layer latticed cylindrical shell[J]. Journal of Harbin Institute of Technology, 2013, 45(2): 14-19.
[18] 张辉东, 王元丰. 基于能量指标的高层钢结构动力弹塑性抗震能力研究[J]. 土木工程学报, 2012, 45(6): 65-73. ZHANG Huidong, WANG Yuanfeng. Energy-based study on the dynamic elastic plasticity seismic capacity of a high-rise steel structure [J]. China Civil Engineering Journal, 2012, 45(6): 65-73).
[19] 张明, 张瑀, 周广春, 等. 基于应变能密度的单层球面网壳结构失效判定准则[J]. 土木工程学报, 2014, 47(4): 56-63. ZHANG Ming, ZHANG Yu, ZHOU Guangchun, et al. Criterion for judging failure of single-layer latticed dome based on strain energy density[J]. China Civil Engineering Journal,2014, 47(4): 56-63.
[20] 宋雅桐, 朱继澄. 地震动持续时间对多层结构反应的影响[J]. 地震工程与工程震动, 1983, 3(4): 49-58. SONG Yatong, ZHU Jicheng. Effects of ground motion duration on earthquake response of multistory structures[J]. Earthquake Engineering and Engineering Vibration,1983,3(4):49-58.
Combined method for predicting the dynamic failure of single-layer latticed dome
ZHANG Ming1, ZHANG Yu2,3, HUANG Yanxia1,ZHOU Guangchun2,3, YU Deguang4
(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology),Ministry of Education, Harbin 150090, China;3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;4. China Enfei Engineering Corporation, Beijing 100038, China)
A combined method was developed which can predict the dynamic instability modes and failure load of a single-layer latticed dome according to the seismic instability modes and failure load of a base dome. Firstly, the finite element models of single-layer latticed domes were built to calculate their full time-range seismic responses inclusive of the nodal displacements and the strain energy density of all the elements corresponding to each load step at individual seismic intensities. Then, the combined method was applied to predict both the dynamic instability modes and failure load of unseen single-layer latticed domes based on the dynamic instability modes and failure load of the base domes. The predicted results were compared with the corresponding fine finite element analysis (FEA) results of the unseen domes. To an extent, the developing combined method could be used in predicting the dynamic instability modes and failure load of the similar kinds of single-layer latticed domes with different spans, different rise-span ratios and different member section sizes. Hence, the study explores the application of the method of cell automat (CA) in the analysis and prediction of the instability modes and failure load of single-layer latticed domes, combining with the existing fine FEA numerical data of the domes.
combined method;single-layer latticed dome;harmonic ground motion;dynamic instability mode;failure load
国家自然科学基金(51608452);中央高校基本科研业务费专项资金科技创新项目(10101B10096040);西南交通大学峨眉校区高层次人才队伍建设科研支撑项目(10101X10096070)
2015-11-30修改稿收到日期:2016-02-03
张明 男,博士,讲师,1983年生
周广春 男,教授,博士生导师,1958年生
05.45
A
10.13465/j.cnki.jvs.2017.06.008
