等距映射和局部线性嵌入算法集成的转子故障数据集降维方法

陈鹏飞， 赵荣珍， 彭 斌， 李坤杰

(兰州理工大学 机电工程学院 机电信息智能技术研究所， 兰州 730050)

等距映射和局部线性嵌入算法集成的转子故障数据集降维方法

陈鹏飞， 赵荣珍， 彭 斌， 李坤杰

(兰州理工大学 机电工程学院 机电信息智能技术研究所， 兰州 730050)

经数据分析途径实现机器智能的故障决策引发出了关于故障数据集的降维问题。通过将等距映射算法(Isometric Mapping，ISOMAP)、局部线性嵌入(Locally Linear Embedding, LLE)算法的优缺点进行互补，提出一种适用于非线性数据集降维的核框架下等距映射与局部线性嵌入相结合的KISOMAPLLE算法。该算法能够同时满足全局距离保持性和局部结构保持能力的数据降维基本要求。用典型的人工数据集和转子故障数据集进行的降维验证结果表明，该算法能够继承ISOMAP、LLE两种算法的各自优良性能，具有能够显著提高典型非线性数据集分类精度的性能。

故障诊断;流形学习;核方法;特征提取

在机械信息技术中，用于描述机械系统运行状态的特征数据集一般都具有高维、非线性的特点。由此引发的是在利用此类数据资源去实现人工智能决策技术中，面临的首要问题是如何消除干扰故障分类准确率的数据集中冗余特征问题。数据科学领域定义该问题为非线性高维数据集的降维问题。传统的线性降维技术如PCA[1]、LDA[2]等，并不适用于非线性数据集的降维。因此探讨新型的如能够解决好适用于转子系统非线性故障数据集的非线性降维方法，则对科学发展机械信息智能决策技术，具有推动和引领作用。

对于如何解决好关于非线性数据集的降维问题，数据科学研究领域提出的流形学习理论非常具有指导作用。如自TENENBAUM等[3]提出了等距离映射的ISOMAP算法之后，GENG等[4]提出了一种局部线性嵌入的LLE算法，随后还相继出现了局部切空间排列(LTSA)[5]、嗨森矩阵的局部线性嵌入(HLLE)[6]、拉普拉斯变换(LEIGS)[7]等一系列新的适用于非线性数据集降维算法。分析这些算法可发现一个显著的特点，是它们都可以被统一在同一个核框架下[8]去构造适应于特定降维问题的新算法。由于ISOMAP算法是基于全局思想建立起的一种邻域图关系，LLE算法是基于局部思想建立起的一种从高维到低维嵌入之间的映射关系，因此在这两种算法间存在着可进行优势互补相结合的潜在可行性。为此参考文献[9]将它们在核框架下进行了融合，尝试着提出了一种关于图像识别的方法。该项研究成果对如何解决好如机械系统特征数据集的非线性数据集降维问题，非常具有参考借鉴作用。

依据上述分析，本研究欲对ISOMAP算法、LLE算法在核框架下进行融合，用于消除高维、非线性转子故障数据集冗余特征的方法进行探讨。欲为机械信息智能决策技术向科学方向发展，提供参考依据。

1 基本原理简介

基于全局思想建立起一种邻域图关系的ISOMAP算法，与基于局部思想建立起一种从高维到低维嵌入之间映射关系的LLE算法，它们的原理可分别参见参考文献[3-4]。因本研究关注的是在核函数已被融合在两个算法中之后，如何将它们统一在核框架下去尝试建立一种高维、非线性数据集的降维实现方法，而这需依据已考虑了核函数影响的KISOMAP算法、KLLE算法去进行，故在此首先对这两种衍生算法的原理简介如下。

1.1 KISOMAP算法

该算法是在ISOMAP算法中嵌入核函数的结果。它的详细步骤见参考文献[10]。核函数嵌入前后的两算法间的区别，是嵌入核函数后得到的算法需要根据式(6)计算出矩阵K(D2)并构建出矩阵表达式(1)。之后需对式(1)进行下述方式的运算处理。

需设法求出式(1)中所需的最大特征值c*。还需根据c*，构建出式(2)所示的Mercer核矩阵KISOMAP，即

(1)

(2)

式中，当c>=c*时，才能够确保KISOMAP是一个实对称的半正定矩阵。求解出KISOMAP的n个特征向量，并将它们组成为特征向量矩阵V∈RN×n和特征值矩阵Λ∈Rnxn。根据多维尺度(MDS)进行计算，即可得到一种低维的嵌入坐标向量Y，即

Y=Λ1/2·V

(3)

KISOMAP算法中的其它步骤与ISOMAP算法相同。不同之处仅在于需运用MDS中常用的添加常数技巧，求解出实对称、半正定的Mercer核矩阵。

1.2 KLLE算法

M=(I-W)T(I-W)

(4)

KLLE=λmaxI-M

(5)

式中，M是一个实对称半正定矩阵；λmax是W的最大特征值，I为单位距阵，其它过程与LLE算法相同。

1.3 核框架的概念

核框架是多种核映射方法的统称。这一概念的具体定义是：对于不同的非线性降维算法，核方法中关于要求解出低维空间与高维空间之间映射函数的问题，最终都可归结于求解某一核矩阵的特征值与特征向量问题。

2 核框架下ISOMAP与LLE的融合方法设计

根据核函数的性质，不同的核矩阵之间可以进行线性变换，最终形成的新矩阵仍然应该是一个核矩阵[11]。由此可推断出：将不同的核矩阵进行融合得到的应该是一个新的核矩阵。根据参考文献[8]，流形学习算法最终都可以转化为求一个核矩阵的特征值和特征向量问题。因此在它们之间可以通过融合处理，可以设计出能满足特定目标所需要的、最大限度的保持各个算法特点和数据结构的新型核矩阵。这一结论为流形学习算法的融合提供了新的理论支撑和探索方向。

基于此原理，故本研究欲将ISOMAP和LLE这两种经典算法在核框架下进行融合，对设计出能继承这两种算法各自优良特点的新的核矩阵构造方法进行探讨。为此，在本研究中提出的这种新算法我们命名它为KISOMAPLLE算法。它在用于高维非线性数据集降维时，数据处理的算法实施步骤被设置如下：

步骤1 用K邻域法或ε半径法求邻域值K。

(6)

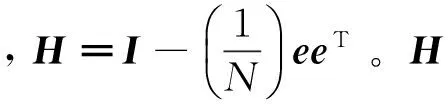
步骤3 按照式(1)和式(2)，提取ISOMAP的核矩阵KISOMAP。本研究中取c=c*，然后按照式(4)、式(5)提取LLE的核矩阵KLLE。

步骤4 由于KISOMAP、KLLE为实对称半正定矩阵，根据参考文献[11]，它们的和也为核矩阵，并引入调节因子α，以调节两种算法的权重。最后根据核函数的性质构建出新的核矩阵KISOLLE，即

KISOLLE=KISOLLE+(1-α)KLLE

(7)

步骤5 计算KISOLLE的特征值矩阵P与特征向量矩阵Q，按MDS计算出低维的嵌入坐标，即

Y=Λ1/2Q

(8)

其中，Λ为P的对角矩阵。

本文算法是在文献[9]的基础上，对ISOMAP与LLE进行融合，其与文献[9]的主要不同在于对ISOMAP的核矩阵的提取过程不同，其他过程则类似。文献[9]根据在连续流形结构中，数据点间的测地距离与欧氏距离的成正比关系将式(6)直接作为ISOMAP的一个核矩阵，融合后将其应用到人脸识别中；本文算法则是将式(6)组成一个Mercer核矩阵并求其最大特征值，然后根据核函数的性质构造出一个新的核矩阵，将其融合后应用到人工数据集与转子故障诊断中。

3 实验结果及分析

3.1 在人工数据集的应用及分析

为了验证第2节提出的KISOMAPLLE算法在高维非线性数据集降维时的有效性，在研究中我们采取的对策如下：采用将在数据科学研究领域已得到认可的若干降维算法与本研究所提出的算法性能进行对照，将选定的若干算法使用在标准的典型人工数据集上。验证过程中选择的算法和典型人工数据集的具体情况如下。其中，用于佐证本算法有效性的系列算法包括7种：{①ISOMAP; ②KISOMAP; ③KISOMAPLLE; ④LLE; ⑤KLLE; ⑥HLLE; ⑦LEIGS}；这7种算法分别被应用在6种典型的人工数据集上：{swissroll、square、puncted_sphere、scurve、gaussian、spiral}。受篇幅所限，图1中仅列出了算法“②”、算法“③”、算法“⑤”，在选定的三种数据集：{scurve、square、puncted_sphere}上的降维效果情况。这三种算法的特点是它们均已嵌入了核函数。在此，邻域值K和权重因子根据多次上机实验结果确定的，被统一设置为K=13、α=0.7。

图1中，子图(a)、(b)和(c)分别是算法“②”、算法“③”和算法“⑤”在选定的三个数据集上的降维结果情况。图1特点是算法“②”、“③”、“⑤”都能够成功实现降维，但算法“③”效果较差，它的最大问题是数据内部出现了“孔洞”现象。虽然算法“①”也会因邻域值取得过小使得数据之间因不连通而出现类似情况[12]，但在实验中我们发现：邻域值的大小对本算法的影响不大，怎么解决“孔洞”问题在本研究中不予考虑，它是本项研究中下一步试图进行深入探讨的内容，然而本研究对其鲁棒性做了下面研究。

(a)KISOMAP算法的降维结果

(b) KLLE算法的降维结果

(c) KISOMAPLLE算法的降维结果

为对比图1所涉及到三个算法的鲁棒性，在实验时我们分别将幅值为0.1、0.2、0.3、0.4、0.5的随机噪声加入在选定的六个数据集中之后再去进行降维。因算法“④”在puncted_sphere数据集上的降维效果较好，故选择这一降维结果作为对比的参照物，并进行了数据降维。实验时对puncted_sphere加入了幅值φ=0.3的随机噪声进行干扰。此时用算法“③”、算法“④”对puncted_sphere数据集进行降维的结果见图2。 图2(a)是puncted_sphere原始数据集的分布状态；图2(b)是对puncted_sphere加入幅值为0.3的随机噪声图；图2(c)为KISOMAPLLE和LLE对puncted_sphere加入0.3的随机噪声降维结果图。通过对比可知，用算法③降维之后还可以保持一定的数据结构，而算法“④”已完全丧失了数据结构。上述实验说明，本研究提出的算法“③”，即KISOMAPLLE算法对于受噪声污染的数据集有一定的鲁棒性。

图2 KISOMAPLLE和LLE在随机噪声为0.3的puncted_sphere数据集上的降维效果Fig.2 Dimension reduction of KISOMAPLLE and LLE on a puncted_sphere set with 0.3 random noise

3.2 在转子故障诊断中的应用情况

本研究选定的研究对象是一套双跨转子系统试验台[13]。实验模拟了五种典型的故障状态类型，即：{正常、不平衡、不对中、碰摩、松动}。特征提取是在对采集到的故障信号进行消噪之后进行的。关于描述该套转子系统故障状态的原始故障数据集的具体构造情况如下。

3.2.1 特征提取与数据降维

本研究对模拟的转子的5种常见故障状态，每种状态80个样本。为了使提取到的数据集能全面客观地反映出不同机械运行故障状态间的差别，为此，对每个通道的信号都提取了表1所示的包括时域、频域、时频域的总共36个特征，用12个通道的表1特征按顺序去构造样本。最终组成的原始故障数据集是规模为400×432维的矩阵。

表1 单个通道信号的统计特征情况Tab.1 Statistic feature

为了剔除原始数据集中的冗余和干扰分类精度的不相关特征，对数据集依据可分性指标大于0.6的原则进行了特征初步选择[14]，共筛选出第{16,28,31,47,11,4,7,16,28,4}共11个特征。即从原始的432维空间中，提取第{16,28,31,40,43,47,76,79,88,100,112}列作为本研究所提出算法输入的原始数据集，图3为其中两个通道的特征选择情况。

图3 通道1和通道2特征选择Fig.3 Channel 1 and channel 2 feature selection

将上述所提取得到的数据分别用3.1节中使用的7种算法，再加上⑧KPCA进行数据降维。其中，权重因子统一取α=0.7，算法“④”、算法“⑤”、算法“⑥”的邻域值均取K=8，其它算法均取K=13，结果如图4所示。其中，“o”、“+”、“*”、“·”、“▽”分别表示不对中、不平衡、碰摩、松动和正常五种状态。

图4 八种降维方法在转子故障数据集中的降维Fig.4 Eight kinds of dimensionality reduction methods in dimensionality reduction of rotor fault data set

3.2.2 实验分析

根据类间可分性判据[14]，同类样本的类内距离越小，异类样本子集合间的距离越大，则说明数据的可分性越好。依据此标准，分析图4可得出以下结论：(1)除算法“⑥”、算法“⑦”外，其他算法都能成功实现降维及分类；(2)算法“③”、“④”、“⑤”的分类效果最好。其中，算法“④”和“⑤”对不平衡、碰摩和正常这三种状态降维效果较好，但后面的实验表明它们会随邻域K的变化出现波动，鲁棒性较差；(3)算法“①”～“③”中，算法“③”的效果最好。其中，在算法“①”降维结果中不平衡、碰摩和正常三种状态类间距较小，不易于分类；算法“②”中的类间距大于算法“①”的，但类内距较大，说明核函数有利于异类样本的分类，但在一定程度上会增大同类样本间的距离；而对于算法“③”，其内类距较算法“①”和“②”更小，类间距更大，即可分性指标更好，说明算法的“③”即继承了算法“①”的全局距离保持特性，又继承了算法“④”的局部结构保持能力，使其类内距不因算法“①”的全局保持能力而变得过于分散，更便于分类；(4)算法“⑧”可以将五种状态分离，从图4可知其类间距要小于算法“③”降维结果的类间距，可分性较要次于本研究所提出的算法。

因上述实验均是在各算法取单一领域值时的实验结果，实验结果有一定的局限性，为了更进一步研究本算法的可行性，本实验也对多个邻域值和不同分类器进行了研究，分别取降维后每种状态的前40个样本作为训练集，后40个样本为测试集，分别输入到SVM和粒子群优化的SVM(PSO-SVM)两种分类器中，最后分别对这7种算法随邻域值从5到20变化时的准确率进行记录并求其平均值，结果统计到表2中，然后对每种算法的降维准确率随邻域值和分类器的变化结果绘制出图5。其中SVM用LIBSVM提供的工具箱，其中核函数用径向基核函数，核参c取0.07；PSO-SVM的参数设置为种群规模M=30，惯性权重ω=0.9，c1=2.8，c2=1.3，最大迭代次数itermax=300。

表2 SVM和PSO-SVM的平均分类正确率Tab.2 The average classification accuracy of SVM and PSO-SVM %

图5中用“□”和“○”分别代表SVM和PSO-SVM两种分类器。为了更加显性表示本文算法的分类准确率随邻域的变化时分类器对结果的影响，则绘出图6加以补充说明。综上，从表2、图5的对比结果中可以得出如下结论：

(1)分类器的选择对故障辨识结果有一定的影响。纵向比较显示：用PSO优化的SVM的分类准确率普遍高于SVM，这是由于SVM的参数为一定值，而PSO优化的SVM的参数通过寻优为最优值，从而有较高的故障识别率，这说明分类器的参数选择不同将直接影响分类精度。

(2)算法“③”的辨识准确率最高。横向比较显示：当算法“③”随邻域值从5～20变化时，PSO-SVM对五种状态的平均分类准确率均达到100%，而SVM平均分类正确率也能达到97.062 5%，说明该算法具有较强的故障辨识能力，且对邻域值的依耐性较弱，鲁棒性较强。

(3)算法“④”和算法“⑤”降维结果出现波动现象。当邻域值较小时算法“④”、“⑤”的诊断正确率为100%，但当邻域值在8～15变化时，准确率随之出现大幅度的变动，说明算法“④”和算法“⑤”对邻域的敏感性比较强，鲁棒性较差。

图 5 SVM和PSO-SVM的分类准确率(%)Fig.5 Classification accuracy of SVM and PSO-SVM

图6 KISOMAPLLE的SVM和PSO-SVM的分类准确率(%)Fig.6 Classification accuracy of SVM and PSO-SVM ofKISOMAPLLE

4 结 论

作为两种经典的流形学习算法ISOMAP、LLE，它们已被成功地应用到了很多领域。本研究以核方法为基础，对这两种算法进行结合，然后去解决非线性高维数据集降维、解决好故障数据分类的实现方法进行了探讨。提出了一种可以被统一在同一核框架下的KISOMAPLLE算法。该算法能够继承这两种原始算法的优良特性，在典型的人工数据集、转子故障数据集的降维应用中的使用情况表明，本算法不仅对噪声和邻域的选择具有较强的鲁棒性，而且能够显著增大不同类别数据子集间的距离，可以提高数据子集间的可分性，由此可提高故障分类的准确率。

[ 1 ] BALASUBRAMANIAN M, SCHWARTZ E L. The isomap algorithm and topological stability[J]. Science, 2002, 295(4):7a.

[ 2 ] ZHANG Yun, LI Benwei, WANG Zibin. Fault diagnosis of rotating machine by isometric feature mapping [J]. Journal of Mechanical Science and Technology, 2013, 27 (11) : 3215-3221.

[ 3 ] TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290(5500):2319-2323.

[ 4 ] GENG Xin, ZHAN Dechuan, ZHOU Zhihua, et al.Supervised nonlinear dimensionality reduction for visualization and classification[J]. IEEE Transaction on Systems, Man, And Cybernetics-PartB: Cybernetics , 2005,35(6):1098-1107.

[ 5 ] CHAHOOKI M A Z, CHARKARI N M. Unsupervised manifold learning based on multiple feature spaces [J]. Machine Vision and Applications, 2014, 25:1053-1065.

[ 6 ] ROSMAN G. BRONSTEIN M M, BRONSTEIN A M, et al. Nonlinear dimensionality reduction by topologically constrained isometric embedding[J]. International Journal Computer Vision , 2010, 89: 56-68.

[ 7 ] VAN DER MAATEN L, POSTMA E, VAN DEN HERIK J.Dimensionality reduction: a comparative review [J]. Journal of Machine Learning Research,2007,10(1):1-22.

[ 8 ] HAM J L, MIKE D S. A kernel view of the dimeninality reducation of manifolds [C]∥ Proc of the 21st International Conference On Machine Learning, 2004.

[ 9 ] 张少龙,巩知乐,廖海斌. 融合LLE 和ISOMAP的非线性降维方法[J]. 计算机应用研究, 2014, 31(1):277-280. ZHANG Shaolong, GONG Zhile, LIAO Haibin. Fusion of LLE and ISOMAP nonlinear descending dimension method [J]. Application Research of computers, 2014, 31 (1): 277-280.

[10] CHOI H, CHOI S. Kernel isomap [J]. Electronics Letters, 2004,40(25):1612-1613 .

[11] 杜京义,侯媛彬. 基于核方法的故障诊断理论及其方法的研究[M]. 北京:北京大学出版社, 2010, p1-7.

[12] 雷迎科. 流形学习算法及其应用研究[D]. 合肥:中国科学技术大学,2011.

[13] 霍天龙,赵荣珍,胡宝权. 基于熵带法与 PSO 优化的SVM转子故障诊断[J]. 振动、测试与诊断, 2011, 31( 3): 279-284.HUO Tianlong, ZHAO Rongzhen, HU Baoquan. Based on entropy method and PSO SVM rotor fault diagnosis[J]. Journal of Vibration, Test and Diagnosis, 2011, 31 (3): 279-284.

[14] 张恒,赵荣珍. 故障特征选择与特征信息融合的加权KPCA方法研究[J]. 振动与冲击, 2014, 33(9):89-93. ZHANG Heng, ZHAO Rongzhen. Fault feature selection and feature information fusion weighted KPCA method to study [J]. Journal of Vibration and Shock, 2014, 33 (9): 89-93.

Method for the dimension reduction of rotor fault data sets by using ISOMAP and LLE

CHEN Pengfei, ZHAO Rongzhen, PENG Bin, LI Kunjie

(Institute of Mechanical and Electrical Information Technology, College of Mechano-Electronic Engineering,Lanzhou University of Technology, Lanzhou 730050,China)

The data set for fault diagnosis and decision based on machinary intelligence gives rise to the requirement of dimension reduction in data processing. The algorithms of Isometric Mapping (ISOMAP) and Locally Linear Embedding (LLE) were introduced simultaneously to mutually complement their strong points and weak points, and a new KISOMAPLLE algorithm was proposed. The algorithm can satisfy the requirement of both global distance preserving and local structure preserving ability, and has been used to reduce the dimension of typical artificial data sets and rotor fault data sets. The proposed algorithm inherits the excellent performances of ISOMAP and LLE, and can improve the classification accuracy of typical nonlinear data sets.

fault diagnosis; manifold learning; kernel method; feature extraction

国家自然科学基金资助项目(51675253)；教育部高校博士学科点专项科研基金资助 (20136201110004)

2015-10-12 修改稿收到日期：2016-01-31

陈鹏飞 男，硕士，1989年生

赵荣珍 女，博士，教授，博士生导师，1960年生 E-mail:zhaorongzhen@lut.cn

0TH165.3; TP181

A

10.13465/j.cnki.jvs.2017.06.007