优化药物制剂工艺的多种数据处理方法的研究

李乃智

摘 要：目前在药物制剂领域中对其运用的数据处理方法种类较多，本文主要以领域内相关的文献资料作为分析基础，对其中方差分析、多元回归分析等多种数据处理方法进行分析及总结，对这些数据处理方法在药物制剂中可以起到的优化作用进行探讨，从而确定其在药剂质量控制中的作用。

关键词：药物制剂；数据处理；分析；作用

目前科技的快速发展决定了各类科学理论知识在一定程度上会相互渗透、相互作用，而利用数据处理方法对药物制剂工艺进行优化是领域内重点研究的方向之一。由于在药物制剂生产的过程中，其流程、方法、时间、温度、配比、PH值等都可能影响药物的实际药效，因此在药物制剂工艺使用的过程中需要对各项指标及方法标准进行确定。

一、多种数据处理方法的作用

在实际中使用不同的数据处理方法会对药物制剂实验结果产生不同的影响，对药物制剂中单指标及多指标采用的数据处理方法也有所不同，根据目前药物制剂工艺优化采用的数据处理方法来看，其单指标多采用方差分析法，这种分析方法在多指标数据中并不适用，单独使用会使数据出现偏差，无法起到优化药物制剂工艺的作用，因此可以选择数据处理方法的联用来提高数据结果准确性，为工艺优化提供数据支持。

二、多种数据处理方法

1.方差分析-多指标综合加权评分法

在药物制剂中采用指标是为了保证制剂工艺的准确性、科学性、标准性及规范性，因此在多指标数据的处理上需要根据实际进行加权处理，从而对其进行综合的评分。对各评价指标按其相对重要程度分配系数，然后以累加法、连乘法或加乘法累计总分，根据总分高低排出优劣顺序。目前方差分析-多指标综合加权评分法在实际的使用中计算方法较为繁琐，但是其在药物制剂工艺的评价上有突出重点、结果准确等优点，综合加权评分法所具有的结果分析的特点可以选出方案中最佳的工艺方法。虽然采用方差分析-多指标综合加权法能达到优化工艺的效果，但存在不足。首先，方差分析只依赖于指标值，一旦某点或几个点的指标值误差很大，势必会影响计算结果的可靠性，从而影响数据结果分析的准确性；其次是对实验点的误差大小无法判断；再次，在进行工艺优化时只能从正交或均匀设计表中找出最好点的实验条件作为优化条件，但这未必是真正的优化条件。

2.多元回归分析-效应面法响应面法

这种组合式数据处理方法结合了数学运算及统计方法的优点，其建模可以对药物制剂中的多指标数据进行组合分析。采用多元回归结合效应面法计算，首先可弥补正交方差计算的不足，如回归方程既能明确每个因素对指标的影响，又可判断实验点的实验误差，更有利于结果解释和工艺条件的优化；其次，多元回归分析所需要的试验数量较少，且对于多指标中参数之间的作用可以有效的减少，因此在进行数据处理上较一些其他数据处理方法更加有效，所得计算结果也更加精确。该分析方法符合一般数学多元回归模型：

Y=b0+b1p+b2m+b3pm+b4p2+b5m2

b0～b5是评估模型的参数，p、m表示自变量，Y表示因变量，该多元回归模型能预测自变量与因变量的关系。然后再通過建立连续变量曲面模型，精确地表述因素与响应值之间的关系，对影响制剂工艺的因素水平进行优化和评价。

3.人工神经网络系统（ANN）

ANN是理论化的人脑神经网络的数学模型，能很好地预测多因素多水平非线性关系，很适于解决多元同时优化的问题，广泛应用于药学领域。ANN是复杂的非线性网络模型，不仅可以省略复杂的统计，就能把自变量和因变量结合起来，而且在模拟和预测时，结果偏差均较RSM小。ANN在优化制剂工艺方面，包括网络模型的构建与训练、实验条件仿真及优化两过程。

4.多维空间三角形面积法

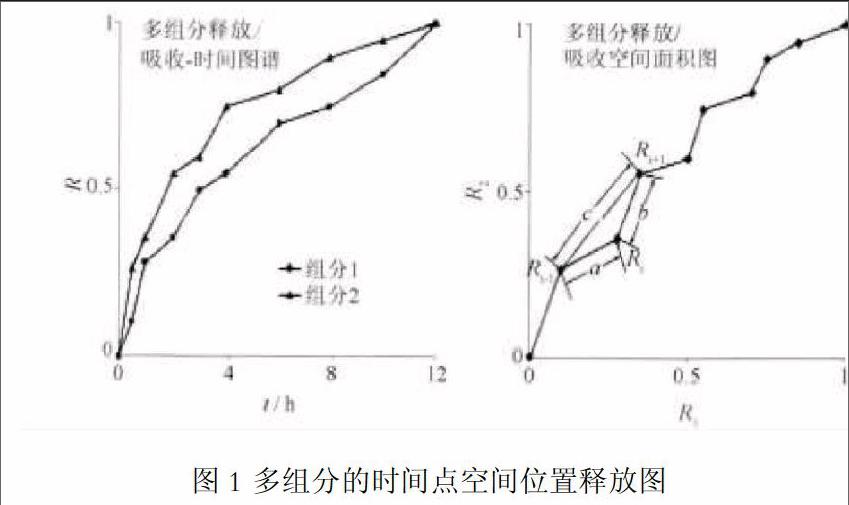
多维空间三角形面积法，即任一时间点，多组分释放度或多组分吸收度是多维空间中的一个点，连续3个时间点连线的三角形面积反映了多组分释放或吸收的动力学变化特征。通过计算多维空间中点与点的距离，得到任意连续3个时间点（释放/吸收）形成三角形的3个边长，进而计算其面积（图1）。以释放度三角形面积累计值-吸收度三角形面积累计值的相关性来表征药物的多组分释放-吸收体内外相关性，而大量文献报道，体内外相关性可用于评价及优化药物制剂工艺。所以，多维空间三角形面积法作为一种新的数据处理方法，在优化药物制剂工艺方面，将会有更广阔的应用前景。

三、展望

药物制剂工艺是非常复杂的过程，方差分析-多指标综合加权评分法、多元回归分析-效应面法、ANN及多维空间三角形面积法都能揭示多因素多水平之间的规律，可以达到优化工艺的目的。

在保证指标值误差不是很大的情况下，选用方差分析-多指标综合加权评分法进行优化更为简单；RSM数据分析结果太依赖于具体的非线性方程，且在模型拟合方面较为困难，所以，在联系不是很复杂且对结果要求不是很高的情况下，运用RSM法进行优化更为实用；ANN是以实验数据为基础，经过有限次迭代计算而获得的一个反映实验数据内在规律的数学模型，且无需目标函数具备明确的数学表达式，并且模型的建立与寻优的过程都可以利用数据可视化技术以直观的图形展现出来，为解决多维非线性系统的优化问题提供了一个全新而有效的途径；多维空间三角形面积法作为一种新的数据处理方法，适合研究物质组分比较明确，且组分在体内外均可检测到的多组分药物。通过大量实验研究及查阅相关代谢组学文献，拟合出代谢组学动态数学模型，即以代谢产物含量为检测指标，来考察影响制备的主要因素，可用于优化多组分中药的制备工艺。目前，多维空间三角形面积法和代谢组学动态数学模型在国内极为少见，随着多学科交叉的渗透以及制剂工艺研究工作者研究水平的不断提高，这两种方法必将得到更广泛的应用。

综上所述，上述的几种数据处理方法在药物制剂中较为常见，根据实际需要应用适当的数据处理分析方法可以补足制剂工艺中存在的不足，并在科学的基础上对这些工艺进行进一步的优化，完善药物制剂工艺，可以为药物制剂的质量提供一定的保障。

参考文献：

[1] 谭素玲.化学药物制剂处方及工艺研究[J].科研，2016（12）：00036-00036.

[2] 田永红.药物制剂工艺分析[J].中国科技博览，2013（17）：234-234.

[3] 徐宇虹，方中坚.药物制剂的优化筛选方法，CN103656688A[P].2014.