基于滑动参数实时估计的履带车辆运行轨迹预测方法研究
2017-04-11熊光明鲁浩郭孔辉陈慧岩
熊光明, 鲁浩, 郭孔辉, 陈慧岩
(北京理工大学 机械与车辆学院, 北京 100081)
基于滑动参数实时估计的履带车辆运行轨迹预测方法研究
熊光明, 鲁浩, 郭孔辉, 陈慧岩
(北京理工大学 机械与车辆学院, 北京 100081)
要实现履带车辆的无人驾驶,在轨迹规划阶段需要准确预测其未来一段时间内的运动轨迹,然而履带与地面之间的滑动使车辆运动轨迹的准确预测变得非常困难。通过研究转向过程中履带接地段的运动,建立基于瞬时转向中心的履带车辆运动学模型。针对车辆的相对位姿是滑动参数的泛函,雅可比矩阵难以求解的问题,通过对泛函微分方程线性化,推导了雅可比矩阵的解析解。根据车辆相对位置计算值和测量值的差值,运用Levenberg-Marquardt算法迭代求解滑动参数,并结合给定控制序列预测未来一段时间内车辆的运动轨迹。该方法不需要提前知道土壤参数,并且能够实时估计滑动参数,以适应路面变化。实车试验结果表明,与传统轨迹预测方法相比,利用该方法预测车辆轨迹时,车辆位置偏差减少30%以上。
兵器科学与技术; 履带车辆; Levenberg-Marquardt算法; 滑动参数估计; 轨迹预测
0 引言
履带车辆由于其优越的通过性和机动性,在军事、农业、火星探测等领域得到广泛应用。履带车辆转向过程始终伴随着高速侧履带的滑转与低速侧履带的滑移[1]。在自动驾驶车辆的局部路径规划中,需要根据车辆模型预测车辆行驶轨迹[2]。相比于轮式车辆,履带车辆的滑动转向特性使行驶轨迹的预测更加困难。因此,研究滑动参数的估计及其对车辆运动的影响对于实现履带车辆的无人驾驶具有重要的理论及现实意义。
目前,国内外学者对履带车辆的转向过程做了大量研究。如国内文献[1,3-5]、国外文献[6-8]建立了履带与地面之间存在剪切作用关系的转向过程模型,并通过实车转向试验验证了所建立模型的准确性。Martinez等[9]建立了履带车辆的近似运动学模型,并利用遗传算法离线计算出滑动参数。Moosavian 等[10]运用实车试验的方法,将滑移率拟合成转向半径的指数函数,并成功应用于车辆的自适应控制。文献[11-13]设计了基于滤波技术的滑动参数估计系统,能够实时估计出车辆的滑动参数,从而提高控制精度。
在之前的文献中,滑动参数的估计都是在控制阶段,用于提高控制精度。本文在轨迹规划阶段估计滑动参数,用于精确预测车辆轨迹。如果在轨迹规划阶段忽略车辆的滑动,生成的待跟踪轨迹将有可能是车辆不可执行的,无论控制精度多高,也将不可避免的产生跟踪误差。
在深入分析履带车辆转向过程的基础上,提出一种基于瞬时转向中心(转向极)的履带车辆运动学模型。通过将泛函微分方程在参考轨迹上线性化计算得到车辆相对位姿的雅可比矩阵,并根据车辆相对位置的计算值和测量值的偏差,运用Levenberg-Marquardt算法实现滑动参数(转向极偏移量)的迭代求解。将当前时刻估计的滑动参数和预测时域内的主动轮转速序列代入运动学模型,从而实现运动轨迹的准确预测。
1 包含滑动参数的履带车辆运动学建模
为了方便分析,图1中列出了履带车辆转向过程中各运动学参数[3,9]。假设履带车辆在水平地面上作平面运动,车辆的质心与几何中心重合,大地坐标系为OXY,X轴指向正东方向,Y轴指向正北方向,车体坐标系Oxy固结于车体上。

图1 履带车辆转向运动学关系Fig.1 Steering kinematic relationships of tracked vehicles
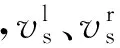
1.1 传统运动学模型
履带车辆是一种典型的差速转向车辆,通过调节左、右两侧主动轮转速,实现航向的改变。定义车辆在大地坐标系下的坐标为P=[XYθ]T,其中(X,Y)表示车辆位置,θ表示车辆航向,fl表示低速侧履带滑移率,fr表示高速侧履带滑转率,则车辆运动学模型为
(1)
式中:
(2)
(3)
由于滑转率、滑移率很难测得,而履带的卷绕速度却可很容易得到,所以当履带车辆在某种路面以不同的速度、不同转向半径转向时,常常将滑转率、滑移率假定为一定值[14]。
然而当低速侧履带卷绕速度为0 m/s,滑移率fl为1,即一侧履带完全制动,车辆做原地转向运动时,无法根据(3)式反求得到牵连速度vMq,从而无法预测车辆的运动轨迹。为了解决这一问题,通过对转向过程中履带接地段的运动学分析,建立基于瞬时转向中心的运动学模型。
1.2 履带及车体瞬时转向中心
履带车辆转向时的一些重要运动学参数都和两侧履带和车体的瞬时转向中心有关[1]。本小节通过分析履带接地段的运动,揭示了各运动学参数与瞬时转向中心的关系。
履带接地段在任一时刻作平面运动,可看作绕瞬时转向中心的旋转运动,所以M、N点的绝对速度可表示为
(4)
(5)
另一方面,M、N点的绝对速度是牵连速度和相对速度的矢量和,此处绝对速度的标量形式为
(6)
(7)
车体作绕瞬时转向中心(xc,yc)的旋转运动,车体上M、N点的牵连速度为
(8)
(9)
由(4)式~(9)式可以计算得到各瞬时转向中心的坐标值为
(10)
(11)
(12)
(13)
(10)式~(13)式描述了车辆转向时,两侧履带及车体的瞬时转向中心与其他运动学参数之间的关系。即使低速侧履带卷绕速度为0 m/s,通过(10)式~(13)式仍然可以反求得到车辆纵向速度、侧向速度和转向角速度,具体推导见(14)式~(16)式。
由于高速侧履带接地段总是滑转,其上任意一点绝对速度的纵向分量与车体的运动方向相反,所以高速侧履带接地段的瞬时转向中心(xr,yr)总是在高速侧履带接地段以外,即yr小于-B/2. 同理,低速侧履带接地段总是滑移,其上任意一点绝对速度的纵向分量与车体的运动方向相同,所以低速侧履带接地段的瞬时转向中心(xl,yl)总是在低速侧履带接地段以内,即yl大于B/2. 当车辆直线行驶时,角速度接近于0 rad/s,(12)式中的yc趋向无穷,而(10)式~(13)式分子分母为同阶无穷小量,所以其他几个瞬时转向中心坐标值为有限值[8]。
1.3 基于瞬时转向中心的运动学模型
通过对履带接地段运动分析得到,车体的侧、纵向速度及角速度不仅与两侧履带卷绕速度有关,还和履带及车体的瞬时转向中心位置密切相关。由(10)式、(11)式及(13)式可以得到车体坐标系下车体纵向速度、侧向速度和转向角速度与瞬时转向中心坐标之间的关系:
(14)
(15)
(16)
于是,履带车辆转向时,基于瞬时转向中心的车辆运动微分方程为
(17)
2 滑动参数估计
2.1 求解思路
由(10)式~(13)式可知,滑动参数(yl,yr,xc)能够通过车体速度和角速度计算得到,但是精确的速度很难通过传感器直接测量得到,而通过差分全球定位系统(DGPS)能够很容易的测量得到车辆的精确位置。本文根据车辆相对位置计算值和测量值的偏差,运用Levenberg-Marquardt方法估计滑动参数,如图2所示。相比于利用速度估计滑动参数,利用相对位置估计滑动参数时,由于相邻两次测量更新时间可以较长,因此能够降低传感器的采样频率[15]。

图2 滑动参数估计框图Fig.2 Block diagram of slippage parameters estimation
假设t1为当前时刻,t0为过去某一时刻,首先计算t0~t1的车辆相对位置计算值和测量值的偏差,并计算雅可比矩阵,然后通过引入代价函数,将滑动参数的求解转换为非线性最小二乘求解问题,最后利用Levenberg-Marquardt方法迭代求解未知的滑动参数。
2.2 车辆相对位姿的计算
车辆位姿包括位置和航向,t1相对t0时刻的车辆位姿可通过对(17)式积分得到:
(18)
式中:g(θ(τ),R(τ))=dP(τ)/dt为车辆运动微分方程;R(τ)=[yl(τ)yr(τ)xc(τ)]T为未知的滑动参数;h(R(ξ))=wz(ξ)为ξ时刻车辆的横摆角速度。
τ时刻车辆的航向θ(τ)不仅依赖于当前τ时刻履带滑动参数,还依赖于历史时刻的滑动参数,因此,车辆相对位姿ΔP是滑动参数R(·)的泛函。需要注意的是,此处R(·)是滑动参数随时间变化的函数,而不是对应于某一特定时刻的函数值。
2.3 雅可比矩阵
雅可比矩阵的计算是滑动参数迭代求解的关键。在任意τ(t0<τ 图3 滑动参数扰动引起的车辆相对位姿误差Fig.3 The vehicle’s relative pose error due to slippage parameters perturbation (19) 式中: (20) (21) (19)式是一线性时变系统,由于F(t)和 (22) 式中:δP(t)为t时刻车辆位姿扰动量;δR(τ)为τ时刻滑动参数扰动量;Φ(t,τ)为状态转移矩阵 于是雅可比矩阵为 2.4 滑动参数迭代求解 尽管履带接地段瞬时转向中心随时间和空间不断变化,为了便于求解,假设滑动参数在短时间内保持不变,即R(τ)≡常量(t0≤τ≤t)。 将(18)式离散化为 (23) 式中:ΔT为采样周期。 (24) 参数估计问题转化为求使代价函数最小的未知参数,即 (25) 由于Levenberg-Marquardt算法是一种有效的求解非线性最小二乘问题的迭代解法,尤其适合参数较少的情况下,它吸收了最速下降法和牛顿- 高斯法的优点,既能使总体沿着下降方向进行搜索,又能保证收敛速度较快,所以本文采用该方法求解滑动参数。其迭代公式为 Rj+1=Rj+[(Jj)TJj+λjI]-1(Jj)Tfj, (26) 式中:j为迭代次数;Jj是雅可比矩阵;I为单位矩阵;λ为阻尼因子。 (27) 阻尼因子λ的引入是Levenberg-Marquardt算法成功的关键。当迭代过程中代价函数变大,即F(Rn)>F(R)时,λ快速变大,Levenberg-Marquardt算法近似于最速下降法,使下一步的迭代沿梯度方向进行;当达到全局最小值时,λ迅速减小,算法近似于牛顿- 高斯法,大大提升了收敛速度。 (28) 根据履带车辆的转向特性,将滑动参数限制在一定范围内,yl0 为了验证算法的有效性,利用某型号履带装甲车辆进行了实车试验,试验路面为土路,如图4所示。 图4 试验履带车辆与试验路面Fig.4 Test tracked vehicle and experimental road 数据采集系统包括安装在主动轮上的轮速传感器、高精度DGPS系统、惯性测量单元。其中轮速传感器测量两侧主动轮转速,经换算可以得到左右侧履带的线速度;DGPS系统用来测量车辆的运动轨迹,能精确地记录车辆质心的经纬度,经换算可转化为大地坐标系下的坐标值;惯性测量单元用来测量车辆的航向。履带车辆的结构参数如表1所示。试验中,由驾驶员驾驶车辆,并由传感器同步记录下车辆的两侧主动轮转速、行驶轨迹及航向。试验过程如下:履带车辆以一定速度直线行驶,然后拉动左侧操纵杆,使左侧主动轮完全制动,同时加大油门,使车辆有足够的功率克服转向阻力,实现原地转向,车辆运行轨迹如图5所示。 表1 履带车辆结构参数Tab.1 Structural parameters of tracked vehicle 图5 车辆运行轨迹Fig.5 Moving trajectory of vehicle 4.1 与传统轨迹预测方法比较 传统轨迹预测方法是将滑转、滑移率看作一常量,其数值根据经验确定,然后将未来一段时间内的主动轮转速序列代入运动微分方程式,向前预测车辆运动轨迹;本文提出的方法是基于实时估计的滑动参数对轨迹进行预测。 图6 两种方法预测得到的位置偏差Fig.6 Position errors of vehicle predicted by two methods 从图6中可以看出,忽略履带的滑转、滑移,即f=0时,距离偏差最大。考虑滑转、滑移时,利用传统方法预测轨迹时,滑转率、滑移率为0.3,平均距离偏差最小。利用本文提出的方法,基于实时估计的滑动参数对轨迹进行预测时,轨迹误差最小,平均位置偏差由f=0.3时的0.76 m下降为0.29 m,下降幅度达到61.8%,具体见表2. 表2 平均距离偏差Tab.2 Mean distance errors 车辆运行过程中,滑动参数实时更新,其随时间的变化如图7所示,从图7中可以看出,左、右侧履带横向偏移量Δyl、Δyr的绝对值在0~1 m内波动,车体瞬时转向中心的纵向偏移量xc在1 m上下波动。其中,Δyl=yl-B/2, Δyr=yr+B/2. 图7 滑动参数估计值Fig.7 Estimated slippage parameters 4.2 预测时域长度与预测轨迹误差的关系 在履带车辆自主驾驶过程中,每一个周期规划的路径长度是影响其自主性能的一个重要因素。规划的路径越远,系统越能够提前判断前方情况从而做出决策。图8描述了分别利用传统方法和基于实时估计滑动参数的方法预测轨迹时,得到的位置偏差及偏差减少率与预测时域长度的关系。由4.1节可知,利用传统方法预测轨迹时,滑转率、滑移率为0.3,平均距离偏差最小,所以图8中令f=0.3. 由于向前预测轨迹时所用模型与真实车辆模型不可避免的存在误差,所以随着预测时域长度的增大,预测的车辆轨迹与真实轨迹间的偏差不断增大,但是相比于传统方法,利用当前估计的滑动参数进行轨迹预测,预测误差显著减小,偏差减少率随预测时域增大而减小,偏差减少率在30%~70%之间。 图8 位置偏差及偏差减少率Fig.8 Position and reduction rate errors 1)提出了一种基于瞬时转向中心的运动学建模方法,解决了当低速侧履带主动轮转速为0 r/min时,传统的基于滑转率、滑移率的运动学模型不能根据主动轮转速反求车体速度的问题。 2)将滑动参数的求解转化为非线性最小二乘求解问题,利用Levenberg-Marquardt算法迭代求解未知的滑动参数。实车试验表明,在土壤参数未知的情况下,本文提出的方法能够显著降低车辆的预测轨迹误差。 3)在1~4 s的预测时域内,本文方法显著优于传统方法,但是优势随着时域的增大而减弱。因此,如何在较大时域内提高车辆轨迹的预测精度是下一步的研究重点。 References) [1] 芮强, 王红岩, 王钦龙,等. 履带车辆转向性能参数分析与试验研究[J].机械工程学报,2015,51(12):127-136. RUI Qiang, WANG Hong-yan, WANG Qin-long, et al. Research on the acquisition of steering performance parameters of armored vehicle based on experiments[J]. Journal of Mechanical Engineering, 2015,51(12):127-136. (in Chinese) [2] 姜岩, 王琦, 龚建伟,等. 无人驾驶车辆局部路径规划的时间一致性与鲁棒性研究[J].自动化学报, 2015, 41(3):518-527 JIANG Yan, WANG Qi, GONG Jian-wei, et al. Research on temporal consistency and robustness in local planning of intelligent vehicles[J]. Acta automatica Sinica, 2015, 41(3):518-527. (in Chinese) [3] 王红岩, 王钦龙, 芮强,等. 高速履带车辆转向过程分析与试验验证[J].机械工程学报,2014,50(16):162-171 WANG Hong-yan, WANG Qin-long, RUI Qiang, et al. Analyzing and testing verification the performance about high-speed tracked vehicles in steering process[J]. Journal of Mechanical Engineering, 2014,50(16):162-171. (in Chinese) [4] 程军伟, 高连华, 王红岩,等. 履带车辆转向分析[J].兵工学报,2007,28(9):1110-1115. CHENG Jun-wei, GAO Lian-hua, WANG Hong-yan, et al. Analysis on the steering of tracked vehicles[J]. Acta Armamentarii, 2007, 28(9):1110-1115. (in Chinese) [5] 李军魁, 王红岩, 芮强. 履带车辆稳态转向性能分析与试验[J].机械工程师,2016 (1): 82-85. LI Jun-kui, WANG Hong-yan, RUI Qiang. Analysis and testing verification the steady state steering performance of tracked vehicle[J]. Mechanical Engineer, 2016 (1): 82-85. (in Chinese) [6] Wong J Y,Chiang C F. A general theory for skid steering of tracked vehicles on firm ground[J]. Proceedings of Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2001, 215(3): 343-355. [7] Said A M,Lakmal D S,Kaspar A. Track-terrain modelling and traversability prediction for tracked vehicles on soft terrain[J]. Journal of Terramechanics, 2010, 47(3):151-160. [8] Wong J Y. Theory of ground vehicles[M]. 3rd ed. NY, US:John Wiley & Sons,2001. [9] Martinez J L, Mandow A, Morales J. Kinematic modeling of tracked vehicles by experimental identification[C]∥ Proceedings of 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems. Sendal, Japan: IEEE,2004:1487-1492. [10] Moosavian S, Ali A, Kalantari A. Experimental slip estimation for exact kinematics modeling and control of a tracked mobile robot[C]∥ 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice, France :IEEE,2008: 95-100. [11] 焦俊,汪宏喜,陈祎琼,等.基于 UKF的农用履带机器人滑动参数估计[J].农业机械学报,2014,45(4):55-60 JIAO Jun, WANG Hong-xi, CHEN Yi-qiong, et al. Estimation sliding parameter of agricultural tracked robot based on UKF[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014,45(4):55-60. (in Chinese) [12] Le A T, Rye D C, Durrant-Whyte H F. Estimation of track-soil interactions for autonomous tracked vehicles[C]∥ Proceedings of the 1997 IEEE International Conference on Robotics and Automation. Albuquerque, NM, US: IEEE, 1997:1388-1393. [13] Yi J, Wang H, Zhang J, et al. Kinematic modeling and analysis of skid-steered mobile robots with applications to low-cost inertial-measurement-unit-based motion estimation[J]. IEEE Transactions on Robotics, 2009, 25(5): 1087-1097. [14] 吴绍斌.遥控履带车辆的转向控制研究[D]. 北京:北京理工大学,2002. WU Shao-bin. Research on steering control of remote tracked vehicle[D]. Beijing: Beijing Institute of Technology, 2002. (in Chinese) [15] Seegmiller N, Rogers-Marcovitz F, Miller G, et al. Vehicle model identification by integrated prediction error minimization[J]. International Journal of Robotics Research, 2013, 32(32):912-931. [16] Kelly A. Linearized error propagation in odometry[J]. The International Journal of Robotics Research,2004, 23(1): 179-218. [17] Kelly A. General solution for linearized systematic error propagation in vehicle odometry[C]∥Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Maui, HI, US: IEEE,2001:1938-1945. Research on Trajectory Prediction of Tracked Vehicles Based on Real Time Slip Estimation XIONG Guang-ming, LU Hao, GUO Kong-hui, CHEN Hui-yan (School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China) In order to realize the unmanned driving of tracked vehicle, its future motion trajectory within a period of time should be accurately predicted in trajectory planning. It is difficult to predict the future motion trajectory of vehicle due to the slippage between tracks and ground. A kinematics model based on the instantaneous steering center is developed by studying the interaction of track and ground. The relative pose of vehicle is a function of the slippage parameters, and the Jacobi matrix is difficult to solve. For this problem, the analytical solutions of Jacobi matrix are deduced by linearizoffing the functional differential equations. Slippage parameters are solved iteratively using Levenberg-Marquardt method according to the calculated and measured pose errors, and a set of input commands is given to predict the future motion trajectory within a period of time. The proposed method is used to update the slip parameters in real time without prior knowledge of terrain parameters. The real vehicle tests show that the position errors predicted using this method are reduced by more than 30% compared to the traditional trajectory prediction method. ordnance science and technology; tracked vehicle; Levenberg-Marquardt method; slippage parameters estimation; trajectory prediction 2016-07-04 国家部委预先研究项目(40401060302) 熊光明(1975—), 男, 副教授。E-mail: xiongguangming@bit.edu.cn TJ810.2 A 1000-1093(2017)03-0600-08 10.3969/j.issn.1000-1093.2017.03.025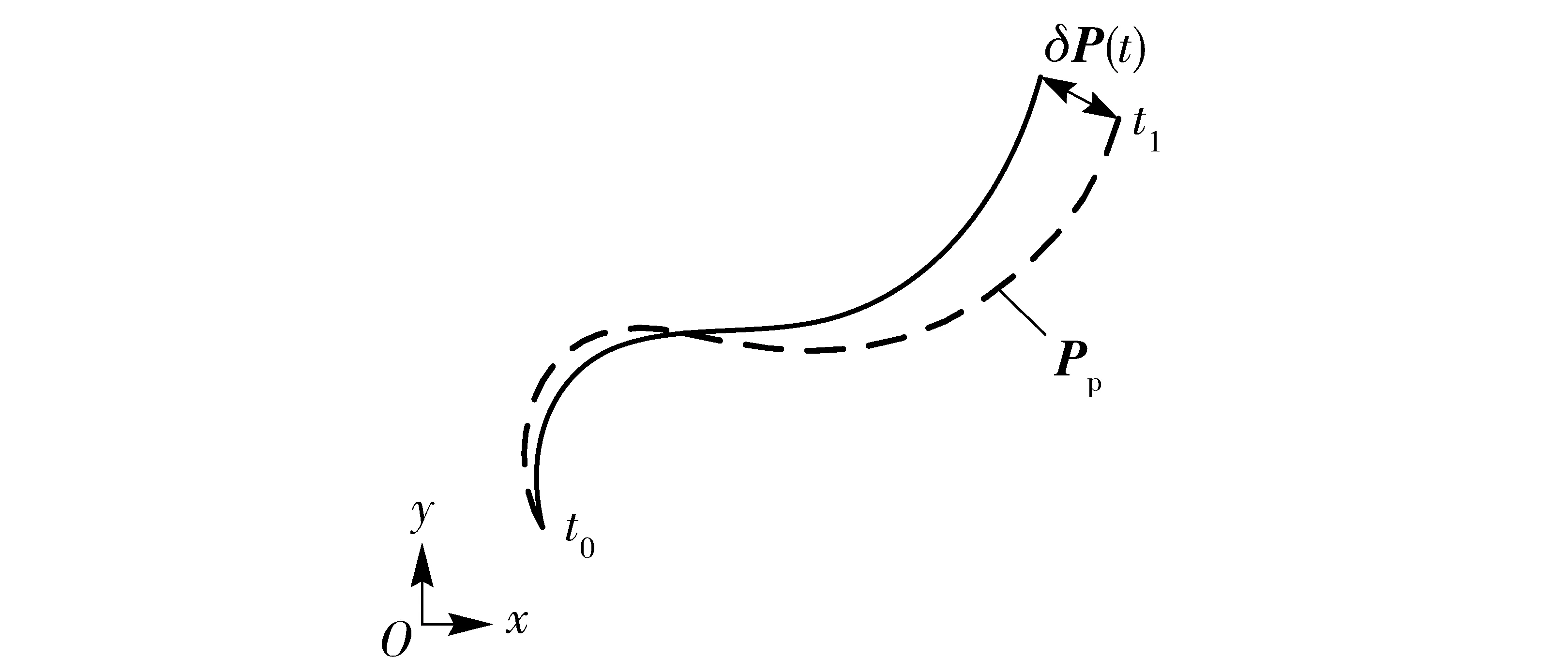
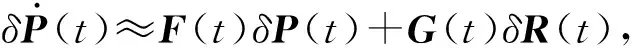
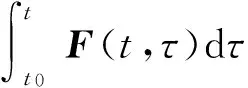
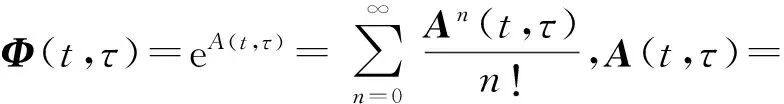

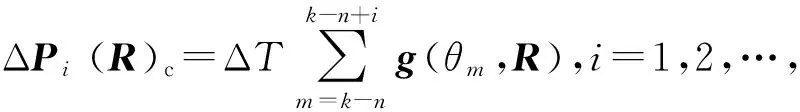
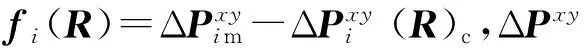
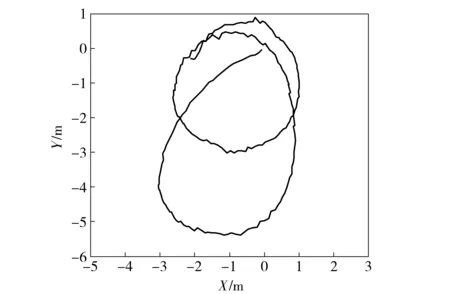
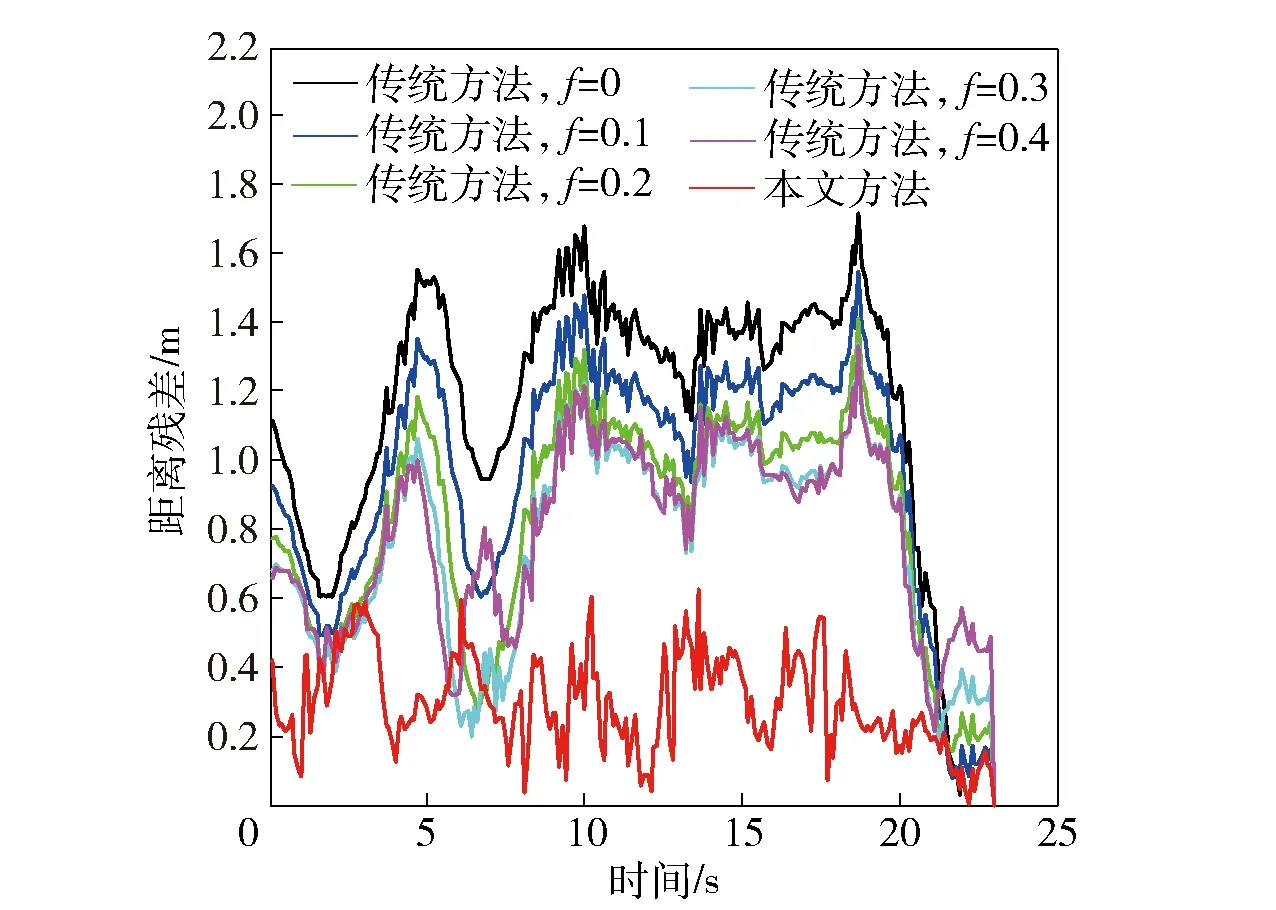
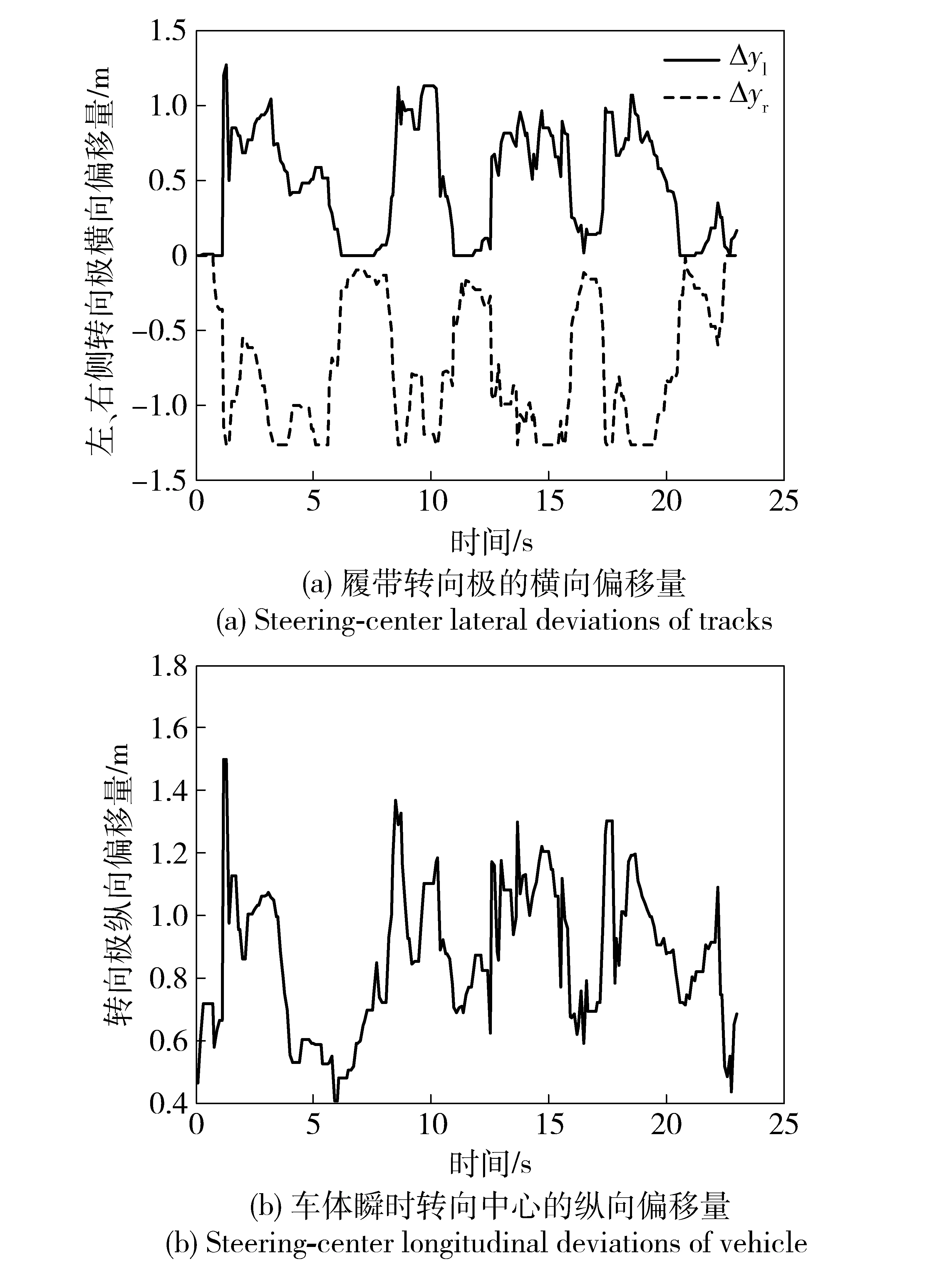
3 轨迹预测
4 实车试验


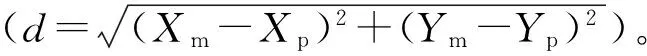


5 结论
