几何画板在初中数学教学中的运用

甘肃省西和县汉源镇初级中学 方向上

几何画板在初中数学教学中的运用

甘肃省西和县汉源镇初级中学 方向上

随着信息化技术的广泛开展，我国各领域、各行业都进入了自动信息化时代，相对应的，为了能够满足信息化飞速发展的人才需求，教学过程中也应该渗透一些信息化思想，提供相应的信息化教学方式，以提高学生对于课堂的兴趣。作为一种新时代下的教学工具和教学资源，几何画板的动态性、高效性和直观性的特点，使它的功能远远高于之前的PPT和Flash，即时操作使它彰显了更大的生命力。本文将从几何画板的四大优势：几何概念认识、活跃课堂气氛、动态思维模式培养和渗透数学思想入手，结合实际的操作案例，对几何画板的应用优势进行详尽的叙述。

一、几何概念认识

对于概念的认识，在数学教学中占据着重要的位置，尤其是在初中数学的学习阶段，有不少数学概念过于接近，学生在学习的过程中容易混淆，如反比例函数和反函数之间的概念混淆，直线与圆的位置关系和圆与圆的位置关系之间的概念混淆等，这些概念在学生学习阶段都是极易被混淆的概念。如果借助几何画板的帮助，理解这些概念之间的区别也就相对简单。比如用几何画板演示直线与圆的位置变化动态过程，固定圆的位置不变，操作让直线从相离的位置慢慢向圆的位置移动，当d=r的时候，此时圆与直线的位置关系变为相切；继续向相同方向移动，当d＜r的时候，圆与直线的位置关系就是相交，有两个交点。在此基础上继续移动直线，分别经历d=r和d＞r，再次让学生们感受直线与圆发生的一系列位置关系，增加学生对于整个动态变化过程的理解。同样的方法，在演示圆与圆的位置关系变化的过程中，固定一个圆，另一个圆分别经历R+r＜d，R+r=d，R+r＜d，R-r=d 和R-r＞d，此时两者之间的位置关系就分别对应为相离，外切，相交，内切和内含。在此过程中，提醒学生留意其中的位置变化情况。除了易混淆的概念之外，几何画板还有利于帮助学生理解难懂的几何概念，比如反比例函数。反比例函数的图象描述中：“无限逼近于坐标轴但是永远不会相交”的描述，一般会困扰学生的认知。对此，任课老师可以进行现场的作图，运用几何画板向学生展示双曲线的特点。具体操作过程如下：目标函数的形式是，所以在作图过程中首先需要建立一个平面直角坐标系，完成后，要在横轴上找出一个点标记为A，之后度量这一点的横坐标值，在操作的“度量”这一菜单中找出“计算”功能，与此同时“度量”功能下的“绘制点”会自动绘制出B点（x，y），这些操作过后，依次操作选中A，B，选择“轨迹”功能按钮进行双曲线的绘制。截止到此，双曲线的图形绘制工作已经完成，为了让学生体验x值的变化带给y值的影响，帮助学生理解“无限逼近但是永不相交”的含义，选中图形中的A点向右拖动，让学生体会到对应图形的走向，结果证明无论x的值变化到何种位置，对应图形都不会与横坐标轴相交。只有通过这样的动态现场演示，才能让学生身临其境地感受和领略几何图形的概念。

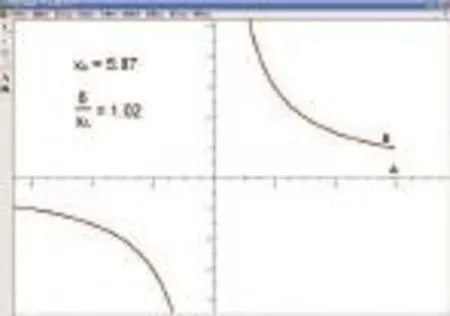
二、活跃课堂气氛

几何画板使学生摆脱了单纯的书本学习，对于几何画板的操作又具有一定的演示效果，能够调动起学生对于演示内容的学习兴趣。在演示的过程中，老师可以邀请有兴趣的同学进行现场的操作，提高学生的参与感。这样一来，学生对于课堂内容就有了一定程度的了解，对于操作机会的争取也使得学习的氛围更加浓厚，课堂气氛更加活跃，有利于学生主动学习。

三、动态思维模式培养

几何画板最明显的优势就是在于其能够显示几何图形的动态变化过程，这一点是它在当今教育领域中被广泛运用的最强大特征。作为一种动态演示工具，几何画板可以生动展示图形之间的位置关系，如上文所说，直线与圆的各种位置关系。其实几何画板的最强大优势不是展现静态的两者位置关系，而是让学生体验动态变化的过程。直线靠近圆的整个动态过程、圆靠近圆的动态变化过程、双曲线上点的横坐标轴发生变化时对应图形的走向等，这些都是体现几何画板动态意义的实例。在初中数学教学中，对于几何认识的要求和课程标准有所提高，这需要学生具备一定的想象能力，如在脑海中想象正方体的平面展开图、圆柱体的平面展开图、折叠部分的图形面积等，都需要学生自身具备一定的空间感和想象力，构造立体动态变化的图形来帮助解决现实问题。在传统的课堂授课中，对于类似的立体图形的展开图，任课老师的教学方法往往是引导学生构建虚拟的立体图形，想象其展开过程，推断展开图形的形状，但这种方法对学生的空间想象能力要求过高，一部分学生难以达到，所以借助几何画板进行动态演示，成为最简便，最高效的教学方法。

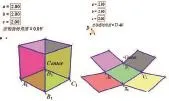
四、渗透数学思想

初中阶段对于数学的学习，在一定程度上会影响到学生整个的学习生涯，在学习过程中，学生只有建立良好的思维模式，养成良好的学习习惯，建立起完善的数学思想，才能帮助学生取得更高的学术成就。几何画板在初中数学教学中的应用，能够帮助学生理解图形变化过程，验证已得定理，制作复杂图形，展示图形内部构造，体验图形走势等，由此渗透给学生一定量的数学思维模式和数学思想。数学思想是学生学习数学科目的凭借，能够帮助学生建立学习的信心。如在习题解决过程中，运用几何画板解决困难问题，体验图形的变化过程。问题如下：如图所示，AB是经过圆心的一条直线，定焦点为A，B，C是位于圆上的一点，并且∠AOC=30度。P是AB直线上的一个动点，且规定该点不与O点重合，直线CP与圆的交点定为Q，那么是否存在一点P使得QO=QP？通过几何画板进行P点的移动，大致判断和寻找相对应的P点。

总之，在当今的初中数学教学中，几何画板的动态性和高效性已被越来越广泛的认可，其功能的强大也被越来越多的接受。作为新时代的新型教学资源，几何画板结合了信息性和演示性的双重特点，有效地提高了教师的授课效率，帮助学生学习相关的理论知识。