初中数学复习教学的有效性探索

贵州省遵义市教育科学研究院 王文霞

初中数学复习教学的有效性探索

贵州省遵义市教育科学研究院 王文霞

数学复习教学是指学生通过自己对已学过的知识进行再呈现、再归纳和再整理，从而对所学知识达到深层理解、学以致用，提高学生的应用能力和思维品质，培养学生的创新意识和实践能力的过程。通过自己对多年的初中数学复习教学的探索，认为复习教学是学生认知的深化和提高，是学生从更高的层面理解知识和掌握技能，进而提高学生数学素养的重要过程。

一、创设合理教学情境，激发学生深层探究

数学复习教学虽不是新授课，但复习教学更需要创设合理的教学情境来保证课堂教学的新颖性、有效性，在教学情境中串起一堂课的主线，让学生自然进入深层次的知识探究学习。

如复习“二次根式”的内容时，为更好地让学生清楚开方时注意正负数的问题，可给学生讲述“蚊子与牛一样重”的故事：从前有一只骄傲的蚊子，总认为自己的体重和牛一样重。有一天，它找到了牛，并说出了体重一样的理由。它认为可以设自己的体重为a，牛的体重为b，则有a²-2ab+ b²= b²-2ab+ a²，左右两边分别化为（a-b）²= （b-a）²，从而有a-b=b-a，移项得2a=2b，即a=b。蚊子骄傲地把自己的理由说完，牛瞪大了眼睛，听傻了！你能帮助牛找出蚊子论证中的问题吗？学生在这样的情境中发现与已有的知识和经验存在的差别和冲突，在认知相悖中激发起了对新知识的探求欲望。为问题饰以背景，在知识的重点和难点处为学生的思维留下点棱角，布下思维的空缺，敦促学生在交叉口形成迫切心理，这样能使学生感到别样的新鲜，产生探索的欲望和积极的学习态度，从而让学生深层探究知识，收到较好的复习效果。

二、巧妙复习章节要点，实现知识厚薄转化

初中数学复习并不是对以前所教的知识进行简单回忆和再现，而是要通过对知识系统的复习，使每一章节中的各个知识点联系起来，找出其变化规律、性质的相似之处及不同点等，从而形成完整的知识体系，达到“以点成线、以线成面、以面成体”的教学目标，使学生对所学知识融会贯通。

按常规的方式进行复习，通常是按照课本的顺序把学生学过的知识，如数学概念、法则、公式和性质等原原本本地复述梳理一遍，这样做学生感到乏味又不易记忆。针对这一情况，在复习概念时，可采用章节知识归类编码法，即先列出所要复习的知识要点，然后归类排队，再用数字编码，这样做可增加学生复习的兴趣，增强学生的记忆和理解，使章节知识实现由量到质的飞跃，实现厚薄之间的转化。如复习“直线、线段、射线”这节内容时，可把主要知识点编码成一个基础、两个要点、三种延伸、四个异同点。这种复习提纲一提出，学生思维立即活跃，有的在思维，有的在议论，有的在阅读，设法寻找提纲的答案，教师趁势把知识进行如下讲解和点拨：（1）一个基础，是指以直线为基本图形，线段和射线是直线上的一部分。（2）两个要点，是指两点确定一条直线、两条直线相交只有1个交点。（3）三种延伸，是指三种图形的延伸，即直线可以向两方无限延伸、线段不能延伸、射线可以向一方无限延伸。（4）四个异同点，是指端点个数不同、图形特征不同、表示方法不同、描述定义不同。事实证明，这种善于转化的复习方法能有效提高复习效率。

三、注重复习方法指导，落实学生创新训练

数学复习教学重要的不是教师讲，而是教师导；不是教师对知识进行系统归类，而是指导学生自己整理归类；不是教师演示，而是学生训练。要使学生牢固、扎实、系统掌握知识，并能够迁移运用，关键在于突出方法的指导。有创新、高效益地组织训练是复习教学设计的一条“主线”。训练要注重对知识创新点的准确把握，围绕知识的创新点，让学生自由发表意见，在学生间引起辩论、评价，达到对知识的灵活运用。通过观察、比较、分析和讨论等方法，最大限度地发挥学生的主观能动性，将知识的巩固、运用、理解、创新贯穿起来。通过练习，让学生实践、反思、领悟，又通过反思让学生重新归纳、总结、升华，举一反三，螺旋上升，促使学生把掌握的知识顺利拓展、高速迁移到其他内容的学习中，成为推动学习迁移，激活认知建构的良性学习循环的有效途径，达到理想化的复习效果。

四、挖掘例题多变元素，提高学生灵活解题

复习课的例题应选择最具代表性和最能说明问题的典型习题，应能突出重点，反映新课程标准中最主要、最基本的内容和要求，要发挥例题以点带面的作用，有意识、有目的地在例题的基础上做系列的变化，挖掘问题的内涵和外延，在变化中巩固知识，在运动中寻找规律，以实现复习的知识从量到质的转变。

如复习“二次函数”内容时，可设计这样一个例题：二次函数的图象经过点（0，0）与（1，1），开口向下，且在x轴上截得的线段长为2，求它的解析式。因为二次函数的图象抛物线是轴对称图形，由题意画图后，不难看出（1，1）是顶点，所以可用二次函数的顶点式y=-a（x+p）2+q，再求得它的解析式（解法略）。变式题（1）：二次函数的图象经过点（0，0）与（1，1），开口向下，且在x轴上截得的线段长为4，求它的解析式。变化后，由题意画图可知（1，1）不再是抛物线的顶点，但从图中看出，图象除了经过已知条件的两个点外，还经过一点（4，0），所以可用y =a（x-x1）（x-x2）的形式求出它的解析式。变式题（2）：二次函数的图象经过点（0，0）与（1，1），且在x轴上截得的线段长为2，求它的解析式。再次变化后，此题可有两种情况：开口向上、开口向下，它的解析式就有对应的两种形式。由于条件的不断变化，使学生不能再套用原题的解题思路，从而改变了学生机械的模仿性，学会分析问题，寻找解决问题的途径，达到在变化中巩固知识，在运动中寻找规律的目的，从而在知识的纵横联系中，提高了学生灵活解题的能力。

五、训练方式多样灵活，增强学生应变能力

复习要重温学过的知识，强化技能，但更重要的是应在原有知识的基础上体现提高与发展。因此，教师要引导和帮助学生应用所学的数学知识去发现问题和解决问题，以创造性的综合训练为手段，以培养学生的创新意识和提高学生的综合应用能力为目标。要选择内容新颖、规律隐藏、思路灵活的习题训练，创造新的思维意境。训练层次要活，采取巩固训练、模仿训练、变式训练和综合训练等灵活方式。训练形式要多，加强“一题多变”和“一题多解”的训练。训练内容要结合复习的实际，在知识的“高度、宽度”上向外拓展延伸，尽可能覆盖知识点、网络知识线、扩大知识面，增强学生的应变能力。

总之，提高初中数学复习教学的有效性，教师要创新已学知识的组合面目、例题元素、方法指导、训练方式、思考角度、理解深度等等，不断让学生温故知新，在复习中体验新见解，创出新收获，开拓新境界。

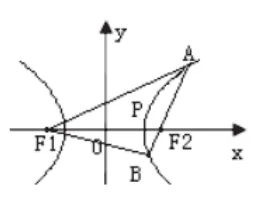
（1）证明：点P的轨迹C是双曲线，并求出方程；

（2）如图，过点F2的直线与双曲线C的右支

交于A，B两点，问是否存在λ使△F1AB是以B为直角顶点的等腰直角三角形？本道例题的解答需要用到数形结合的思想，仅仅通过计算得到答案是非常困难的，但如果采用数形结合的思想，就能够轻而易举地解决，因此为了让学生更加透彻而直观地理解该题，教师可板书画出草图，帮助学生理解题意。

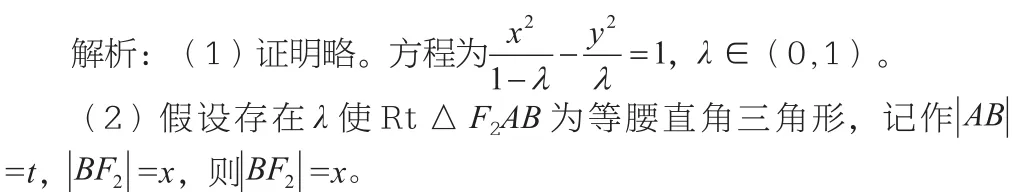
通过图象，学生可以在脑海中更加直观地建立问题模型，更加清晰又充分地解读题意。运用数形结合的数学思想解决圆锥曲线问题，能够大大提高教师的工作效率以及学生的理解效率。图象的运用既能够将抽象问题变得直观化、形象化，也能够帮助学生更加容易地理解题意。

总之，高中数学教学要求教师准确把握各章节知识点的重点和难点，在圆锥曲线知识的讲解中，不可过偏地抓重点和难点，而是要在把握基础知识的前提下，做一些拓展知识的介绍。考虑到圆锥曲线部分的内容难度较大，教师在讲解过程中应当把握好节奏，给予学生适时的鼓励。