基于EMD的改进马田系统的滚动轴承故障诊断

陈俊洵，程龙生，胡绍林，余 慧

(1.南京理工大学 经济管理学院，南京 210094; 2.西安卫星测控中心，西安 710043)

基于EMD的改进马田系统的滚动轴承故障诊断

陈俊洵1，程龙生1，胡绍林2，余 慧2

(1.南京理工大学 经济管理学院，南京 210094; 2.西安卫星测控中心，西安 710043)

为了提高滚动轴承的可靠性、及时发现其潜在的故障，提出了一种基于改进马田系统(MMTS)的滚动轴承故障诊断方法。首先利用经验模态分解(EMD)方法对原振动信号进行分解，得到了多个本征模态分量(IMF)并计算基本模式分量的统计特征集。然后，在此基础上构建基准空间(马氏空间)，针对马田系统在筛选特征变量时效果不佳、基准空间数据的差异性问题，引入粗糙集(RS)筛选有效特征变量改进马田系统,大幅降低特征向量的维数。最后，计算待诊断信号到基准空间的马氏距离，从而完成滚动轴承的故障诊断。利用滚动轴承振动数据对该模型进行了测试，结果表明，该模型与实际相符，可以准确、有效地识别滚动轴承的故障类型。

滚动轴承； 经验模态分解； 改进马田系统； 故障诊断； 粗糙集

滚动轴承是各种旋转机械应用中最广泛的一种通用机械部件，40%的机械故障是由轴承故障引起的[1]。如何获得关于运行状态、故障诊断、维修决策等方面的是研究工作的关键，因此对滚动轴承的状态监测和故障诊断具有重要的现实意义。

ALI等[2]把经验模态分解(Empirical Model Decomposition，EMD)和神经网络结合起来对振动信号进行故障诊断。王录雁等[3]结合灰色关联模型建立本征模函数(Intrinsic Mode Function，IMF)的能量分布与轴承状态之间的对应关系，从而实现轴承的状态识别。WU等[4]采用了(Hidden Markov Model，HMM)和支持向量机的诊断方法。SHEN等[5]将小波变换和支持向量机结合起来进行故障诊断。AO等[6]提出了一种能量熵和支持向量机的故障诊断方法。LIU等[7]提出了一种粒子群优化的小波支持向量机故障诊断方法。以上文献大多将神经网络、支持向量机等模式识别算法对滚动轴承进行故障诊断，该方法依赖于知识库中的现有知识，当一种新的异常征兆出现时，很可能无法找到最佳匹配而不能诊断或者诊断错误。因此，如何寻找一种新兴的模式识别方法是滚动轴承的重要方向。

马田系统(Mahalanobis Taguchi System，MTS)是由田口玄一博士于20世纪90年代首次提出的一种新兴的模式识别方法，是质量工程学的最新进展之一，主要有诊断、评价和预测等三大功能。近年来，马田系统作为多元系统一种潜在的模式信息技术，已在学术界和实际应用中得到广泛认可[8-9]，也有学者将马田系统运用到故障诊断领域。SOYLEMEZOGLU等[10]用实验来证明马田系统在故障诊断、分离、预测中，具有良好的效果。SHAKYA等[11]在提取振动信号的时域、频域等特征的基础上，采用施密特马田系统对滚动轴承做故障诊断研究。HU等[12]从机械信号中提取出多重分形特征，并在此基础上用MTS机械系统进行故障诊断。WANG等[13]提出了SVD—EMD的马田系统的滚动轴承故障诊断方法。然而，上述文章均没有考虑到正常样品的振动信号包含各种载荷的数据，该数据存在着差异性。

综上所述，虽然马田系统在故障诊断方面中已经有了研究，但是总体研究的数量非常少、马田系统的理论体系还不够完善，传统的马田系统在筛选信噪比较大的变量组合其分类效果未必良好[14]。因此，本文提出了一种基于EMD的改进马田系统的方法。首先，通过EMD分解得到IMF函数并由此计算出特征向量，从而构造马田系统的基准空间并确定该空间的有效性。同时为了解决特征向量的高维性和复杂性，引入了粗糙集筛选有效特征变量从而改进马田系统。最后，根据马氏距离来确定滚动轴承的故障类型。

1 EMD方法

在构建马田系统时，需要对特征量的选择。EMD方法从原始信号中提取出若干个IMF分量和一个残余量。IMF分量突出了数据的局部特征，对其进行分析，可以准确有效地把握原信号的特征信息[15]。

EMD 的具体分解过程是：

(1) 假设初始信号为x(t)，找出原信号x所有的极大值点和极小值点，并且拟合出所有的极大值点和极小值点形成的原数据的上下包络线。

综合上面的分解过程，滚动轴承的振动信号x(t)被分解为m个IMF和一个残余分量之和。

(1)

因信号的高频部分集中在前N个主要IMF分量中，能够反映信号的关键信息，故将其留下进行后续特征提取，而对于最后的几个IMF残余分量则需要去除，是因为残余分量以低频噪声干扰为主。

2 改进的马田系统方法

对于轴承故障诊断中获取的多维特征变量，需有效地简化从而提高其计算效率。因此，本文利用改进的粗糙集方法来优化和筛选特征变量，在此基础上用马氏距离对滚动轴承进行故障诊断。

本文提出的改进马田系统方法(Modified Mahalanobis Taguchi System，MMTS)方法主要有4个步骤，具体步骤如下:

步骤1 基准空间的构造

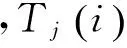
(1) 计算正常样本数据矩阵A中各IMF分量的均值和标准差，

(2)

(2) 利用μj和sj对样本数据矩阵A进行标准化，

(3)

从而得到标准化矩阵

(3) 计算属性间的相关系数矩阵，

(4)

(4) 计算属性间的相关系数矩阵S的逆矩阵S-1。

(5) 计算所有正常样品的马氏距离

(5)

步骤2 确认基准空间的有效性

由马氏距离性质可知，基准空间中正常样品的马氏距离应分布在1附近，至多不会超过某个临界值。然而，训练样本中异常样品的马氏距离应大于临界值，且马氏距离随着样品与基准空间差异性的增大而增大。如果满足上述规则，说明选取的基准空间是合理的，能够将正常样品和异常样品较为明显地区分开来，以此规则检测基准空间的有效性

步骤3 粗糙集优化基准空间

基准空间中设备运行状态可以由多个特征变量表示，但并非所有的原始特征变量对设备的运行状态分类都具有很强的表征能力。因此，需要对进行系统优化。

传统马田系统筛选使用了正交表和信噪比来优化基准空间，其分类效果未必良好，并未考虑到基准空间数据的差异性，而滚动轴承的正常信号数据中，可能存在不同载荷的数据。粗糙集[16-17]擅长处理不完善、不确定数据等不完全信息，可以在保持分类能力不变的前提下快速地对属性进行约简，删除冗余属性、消除过剩规则，可以在保留绝大部分有用信息的前提下，减少变量个数，大大简化了数据的复杂度。因此，本文将粗糙集应用于马田系统中筛选有效待征变量。

本文的具体思路如下：

(1) 离散化

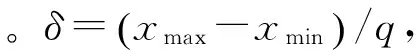
(2) 构建决策表

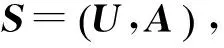
(3) 遗传算法的属性约简

一个信息系统中往往存在许多属性是重复的和冗余的，需对信息系统中的属性表述进行约简，约简的目的在于使信息表述中不包含多余的属性，同时确保最小属性集分类的正确性，即约简后的信息系统属性表述既最简洁又正确。

约简方法一般为基于可辨识矩阵(计算复杂度大，不适合海量数据)、贪心算法(无法获得最优约简组合)来进行约简。然而滚动轴承的振动信号中，测量参数多和样品数多导致决策表规模较大时，粗糙集的一般约简方法不适合，因此，本文采用了以遗传算法编程约简决策表的属性和属性值，得到优化后的基准空间。对于评价指标约简问题，本文采用{0，1}符号集的二进制一维编码形式。

在粗糙集的属性约简中，约简后的属性集需要满足两个条件：即保持原分类质量不变和属性集中不含有冗余属性，所以粗糙集的属性约简是一个多约束、多目标的优化过程。因此适应函数设计应该包含以下两个目标：一是搜索变量个体必须满足分类质量，通常要求必须是约简：二是个体所包含的属性个数要尽量少，见式(6)。

(6)

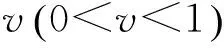
步骤4 故障诊断

计算待监测的样品到经过MMTS优化后空间的马氏距离，从而根据马氏距离来判断故障类型。

3 基于EMD的改进马田系统的故障诊断方法

本文建立的滚动轴承的故障诊断模型有2个基本部分：EMD和MMTS。其中，EMD用来提取出振动信号的特征分量，MMTS用来筛选出有效的特征变量并且用来故障诊断。见图1，具体步骤如下：

步骤1 对采集的滚动轴承的正常信号和故障信号分别进行EMD分解，得到多个IMF函数和残余分量

步骤2 把分解后得到的正常信号分成M1段，故障信号分成M2段。分别计算前N个IMF分量的均方根、极差、能量和峰度(公式见表1)，其中，n为每个样品的采样点。xi为第i个采样点的数值。从而构建了4N高维度特征向量。

表1 选择的特征Tab.1 Selected characteristic value

步骤3 将正常状态的信号M1×4N作为基准空间，故障信号M2×4N用来确认空间的有效性。根据第2节中改进马田系统方法的步骤三，用粗糙集来优化筛选特征变量，大幅降低特征向量的维数

步骤4 计算待评估的样品到优化后基准空间的马氏距离，从而完成对滚动轴承的故障诊断。

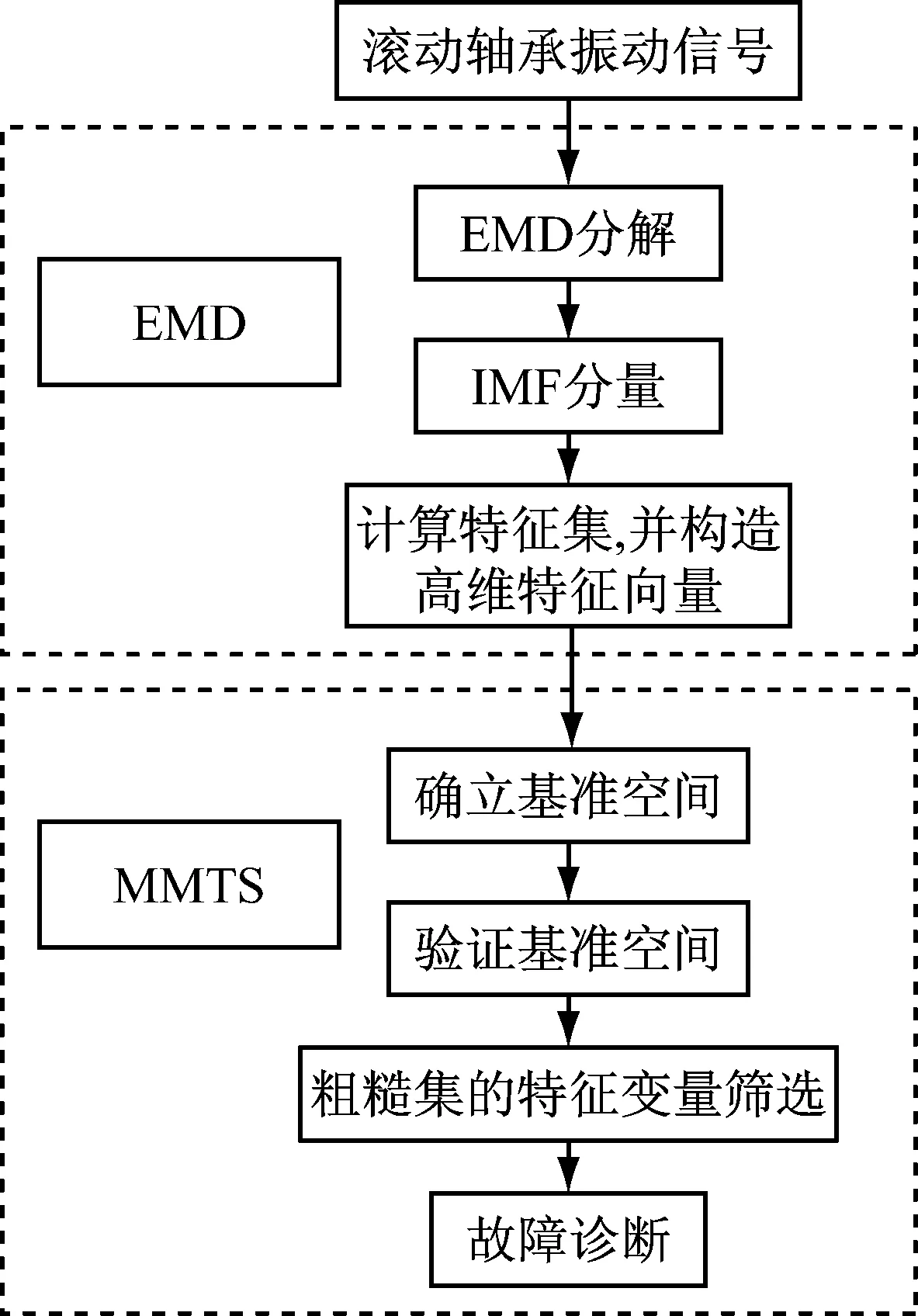
图1 EMD-MMTS流程图Fig.1 Flow diagram of EMD-MMTS

4 实验与分析

4.1 实验说明

实验采用美国凯斯西储大学(Case Western Reserve University)电气工程实验室的滚动轴承故障模拟实验台采集的轴承数据[18]。待检测的轴承(驱动端轴承)支撑着电动机的转轴, 型号为 SKF6205-2 RS，如图2所示(轴承内径为25 mm, 外径为 52 mm，厚度为15 mm，节径为39.04 mm, 滚动体直径为 7.94 mm, 接触角为0 °，滚动体个数为 9)。

为了验证方法的有效性，在实验中分别随机获取正常轴承数据和一种轴承故障的振动数据。以长度1 024个采样点的数据为一个样品。其中，正常状态下总共采集200个样品作为初始的基准空间，故障状态下的采集100个样本作为确认空间的有效性。

图2 实验装置Fig.2 Experimental apparatus

4.2 实验步骤

对采集到的样品进行EMD分解后，得到了IMF分量，其中一个样品的信号分解如图3所示。其中signal为原始信号，IMF1，MF2，……,IMF7为各个特征本分量，RES为余项，横轴代表采样点，纵轴代表加速度幅值。见图3。从图3中看出前4个IMF分量包含主要的高频分量，剩余分量中包含了低频信息。因此，本次研究选取这4个分量为特征集来源。

图3 EMD分解后的特征分量
Fig.3 Character component of decomposed EMD

在本文选取的IMF1—IMF4分量基础上，再分别计算其相应的4个统计特征值，依次是均方根、极差、能量、峭度，即从每一个样品中提取出一个16维特征向量。然后，利用公式(2)～(5)计算每一个初始特征变量的均值、标准差和变量间的相关矩阵，并由这些数据组成为基准空间。选取故障数据作为异常样品，用来确立基准空间的有效性。通过计算得到的马氏距离(见图4)，发现正常样品空间大多在1附近，并且和异常样品空间的马氏距离具有很明显的差异，所以基准空间构造是有效的。

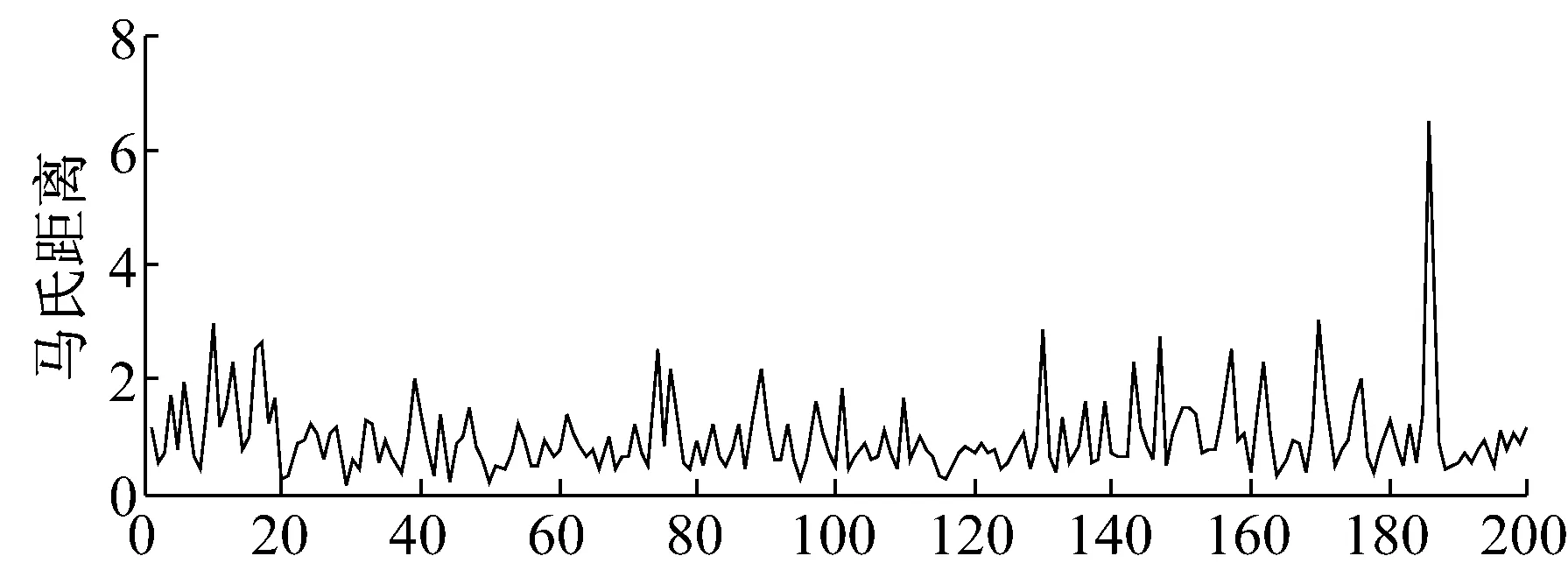
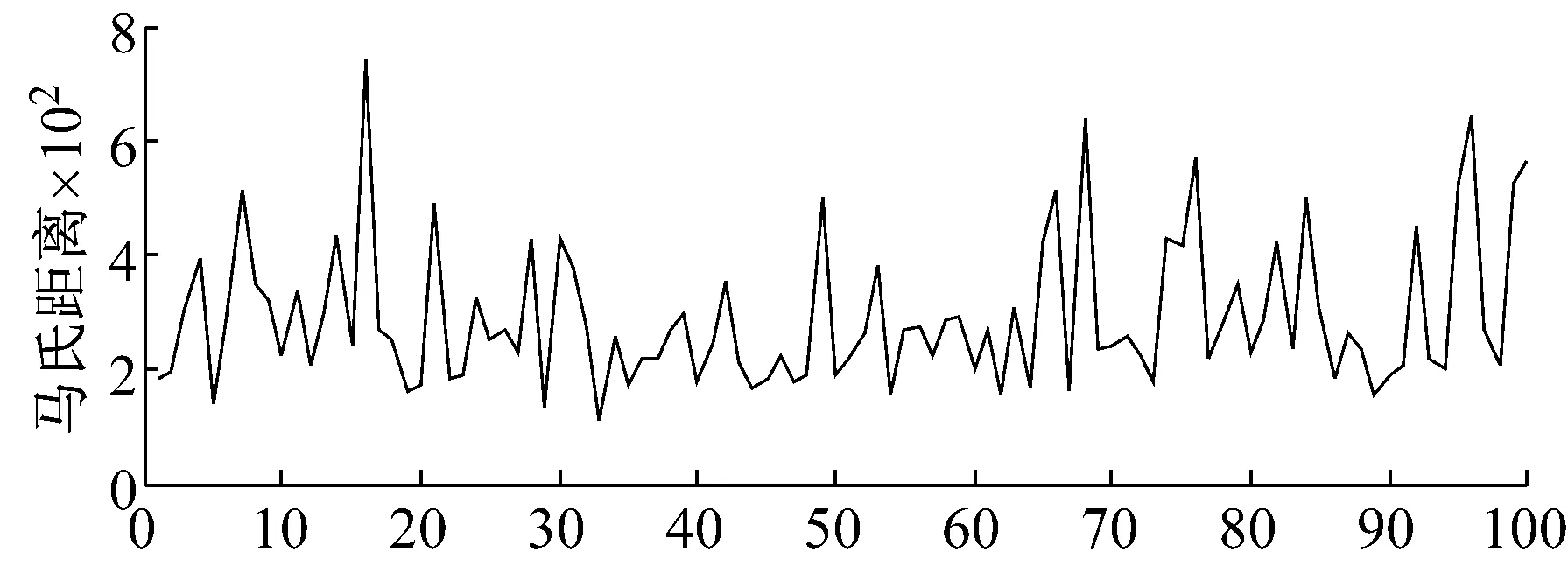
图4 正常样品和异常样品的马氏距离Fig.4 Mahalanobis distance of normal sample and abnormal sample

然后根据粗糙集的约简原理优化和筛选特征变量，在本系统中，条件属性共16个，即16个特征向量；决策属性中，将构建的条件属性离散化，利用等距离散化方法将特征分成4段(有4种不同的荷载)。分别用1,2,3,4代表各个区间，从而构建决策表。

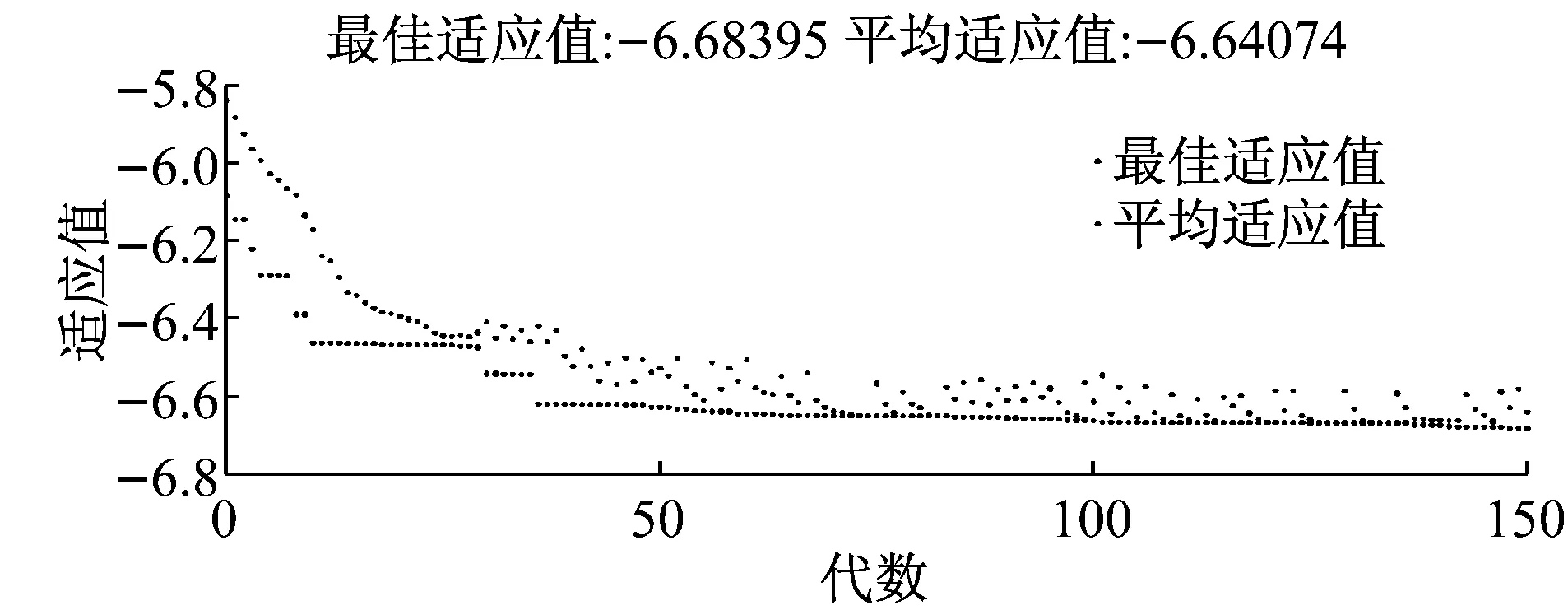
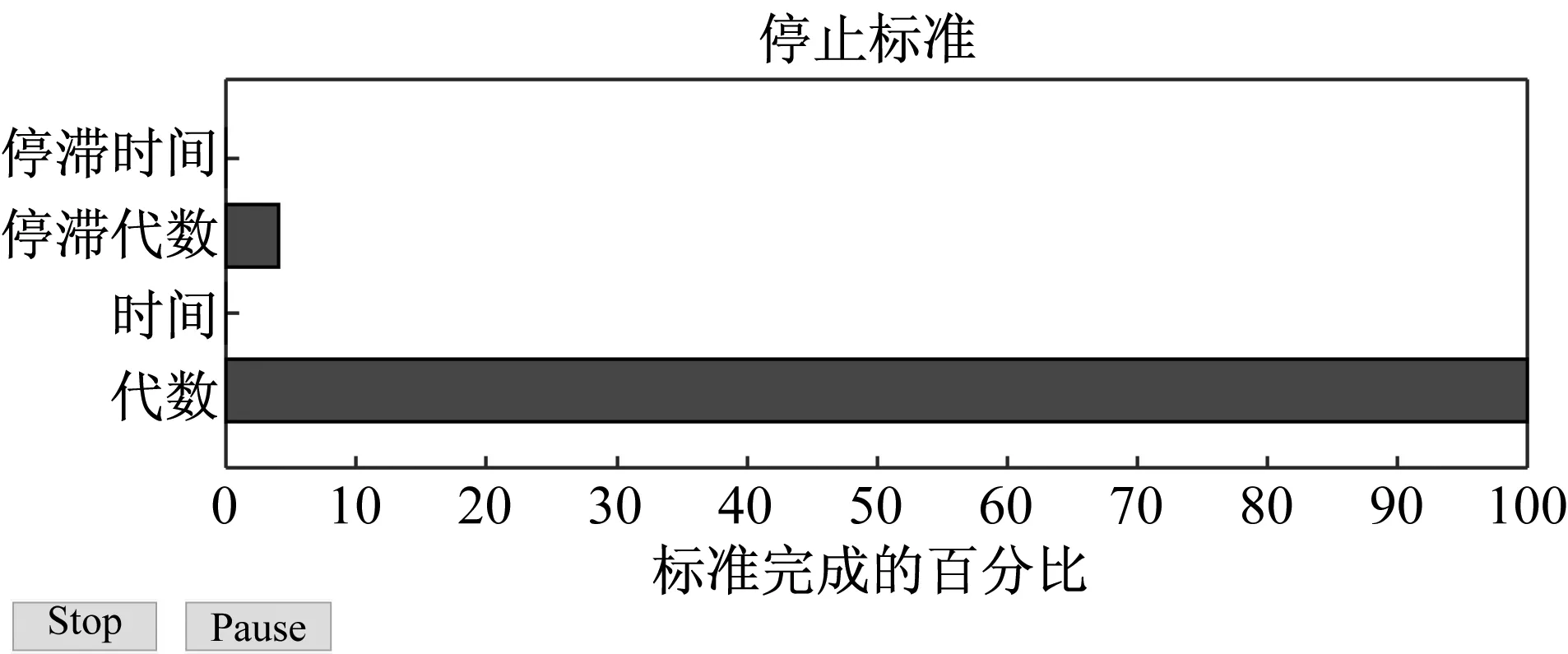
图5 遗传算法的迭代过程图Fig.5 Iteration procedure chart of genetic algorithm

在离散化的基础上，采用基于遗传算法优化的约简属性值方法，对特征属性约简。其中，遗传算法采用二进制编码，目标函数为式(6)所示，种群最大迭代次数为150，用matlab的遗传算法工具箱实现，如图4所示。其中，决策属性对条件属性的依赖度为0.98。

为了验证本文所提出方法的有效性，分别选取正常信号、内圈故障、外圈故障、滚动体故障信号，每组信号分别抽取100个样品，运用马氏距离公式计算每组信号到优化后基准空间的马氏距离，见图6。不同模式下轴承的马氏距离的平均值见表2。

在图6和表2中可以看到，运用EMD-MMTS方法可以很好的区分出滚动轴承的故障。

表2 不同模式下轴承的马氏距离的平均值Tab.2 Average value of Mahalanobis distance in different model

(a) 正常运行样品

(b) 内圈故障样品

(c) 滚动体故障样品

(d) 外圈故障样品

5 结 论

本文提出了基于EMD的改进马田系统的滚动轴承的故障诊断方法，对滚动轴承的振动信号进行EMD分解，在获取的IMF的基础上构造特征分量，从而建立了基准空间。利用MMTS方法优化特征分量，在此基础上，根据马氏距离对滚动轴承数据进行故障诊断。本文提出的方法能够剔除干扰成分、突显故障特征，从而完善了马田系统理论体系、为故障诊断方法提供了一个新的解决思路。案例分析的结果验证了本文提出方法的有效性，该方法为滚动轴承的故障诊断提供了可行途径。

[1] OCAK H, LOPARO K A.A new bearing fault detection and diagnosis scheme based on hidden markov modeling of vibration signals, acoustics, speech, and signal processing[J].ICASSP Proceedings,2001:3141-3144.

[2] ALI J B, FNAIECH N, SAIDI L, et al.Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals[J].Applied Acoustics, 2015, 89: 16-27.

[3] 王录雁，王强 张梅军，等.基于EMD的滚动轴承故障灰色诊断方法[J].振动与冲击, 2014, 33(3): 197-202.

WANG Luyan, WANG Qiang, ZHANG Meijun, et al.A grey fault diagnosis method for rolling bearings based on EMD[J].Journal of Vibration and Shock, 2014, 33(3): 197-202.

[4] WU Bin, YU Shanping, LUO Yuegang, et al.Rolling bearing faults diagnosis method based on SVM-HMM[J].Measuring Technology and Mechatronics Automation,2010,3:295-298.

[5] SHEN C, WANG D, KONG F, et al.Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier[J].Measurement, 2013, 46(4): 1551-1564.

[6] AO H L, CHENG J, LI K, et al.A roller bearing fault diagnosis method based on LCD energy entropy and ACROA-SVM[J].Shock and Vibration, 2014.

[7] LIU Z, CAO H, CHEN X, et al.Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings[J].Neuro Computing, 2013, 99: 399-410.

[8] DAS P, DATTA S.Exploring the effects of chemical composition in hot rolled steel product using mahalanobis distance scale under mahalanobis-taguchi system[J].Computational Materials Science, 2007, 38: 671-677.

[9] LEE Y C, TENG H L.Predicting the financial crisis by Mahalanobis-Taguchi system-Examples of Taiwan’s electronic sector[J].Expert Systems with Applications, 2009, 36: 7469-7478.

[10] SOYLEMEZOGLU A, JAGANNATHAN S, SAYGIN C.Mahalanobis taguchi system (MTS) as a prognostics tool for rolling element bearing failures[J].Journal of Manufacturing Science and Engineering, 2010, 132(5): 051014.

[11] SHAKYA P, KULKARNI M S, DARPE A K.Bearing diagnosis based on Mahalanobis-Taguchi-Gram-Schmidt method[J].Journal of Sound and Vibration, 2015, 337: 342-362.

[12] HU J, ZHANG L, LIANG W, et al.Incipient mechanical fault detection based on multifractal and MTS methods[J].Petroleum Science, 2009, 6(2): 208-216.

[13] WANG Z, LU C, WANG Z L, et al.Fault diagnosis and health assessment for bearings using the Mahalanobis-Taguchi system based on EMD-SVD[J].Transactions of the Institute of Measurement and Control, 2013, 35(6): 798-807.

[14] WOODALL W H, KOUDELIK R, TSUI K L, et al.A review and analysis of the Mahalanobis-Taguchi system[J].Technometrics, 2003, 45(1): 1-15.

[15] SINGH S, KUMAR N.Combined rotor fault diagnosis in rotating machinery using empirical mode decomposition[J].Journal of Mechanical Science and Technology, 2014, 28(12): 4869-4876.

[16] ZHAO N B, LI S Y, YI S, et al.Fault diagnosis based on rough set and BP neural network (RS-BP) for gas turbine engine[C].Advanced Materials Research, 2013, 732: 397-401.

[17] LI N, ZHOU R, HU Q, et al.Mechanical fault diagnosis based on redundant second generation wavelet packet transform, neighborhood rough set and support vector machine[J].Mechanical Systems and Signal Processing, 2012, 28: 608-621.

[18] LOPARO K A.Bearings vibration data set,Case Western Reserve University.http://www.eecs.cwru.edu/laboratory/Bearing/download.htm.

Fault diagnosis of rolling bearings using modified Mahalanobis-Taguchi system based on EMD

CHEN Junxun1, CHENG Longsheng1, HU Shaolin2, YU Hui2

(1.School of Economics and Management, Nanjing University of Science and Technology, Nanjing 210094,China;2.Xi’an Satellite Control Center, Xi’an 710043, China)

In order to improve reliability of rolling bearings and find their potential faults, a method of rolling bearings fault diagnosis based on Modified Mahalanobis-Taguchi System was proposed.Firstly, the original vibration signal was decomposed into several intrinsic mode functions by means of the empirical model decomposition (EMD) and the statistical characteristics of the basic mode components were calculated.Then effective feature variables were screened with rough set aiming at shortages of Mahalanobis-Taguchi system in screening feature variables and the problem of difference in the reference space (Mahalanobis space) data.Mahalanobis-Taguchi System was improved and the number of dimension of the feature vector was obviously reduced.Finally, Mahalanobis distance from a signal to be diagnosed to the reference space was calculated and the fault diagnosis of a rolling bearing was completed.This model was verified using vibration data of rolling bearings.The results showed that this model agees well with actuality and can identify fault types correctly and effectively.

rolling bearings; empirical model decomposition; modified Mahalanobis-Taguchi System; fault diagnosis; rough set

国家自然科学基金(71271114; 61473222)

2016-03-25 修改稿收到日期：2016-08-01

陈俊洵 男，博士生，1989年4月,

程龙生 男，教授，博士生导师，1964年11月

TP181

A

10.13465/j.cnki.jvs.2017.05.024