高速铁路温度场作用下桥上无缝道岔与桥梁相互作用研究
2017-04-10孙加林
孙加林
(中国铁道科学研究院 铁道科学技术研究发展中心,北京 100081)
桥上无缝道岔与桥上无缝线路有很大的区别。从线路结构看,桥上无缝线路的线路形式比较单一,在全桥范围内,每跨梁上的线路情况均相同;而桥上无缝道岔则不同,由于道岔结构的复杂性,使每跨梁上的线路情况均不相同。因此,在设计时必须考虑道岔和桥梁的相互作用。桥上无缝道岔结构作为跨区间无缝线路的关键结构,其传力机理比路基无缝道岔和桥上无缝线路更为复杂。以往试验研究确定了无缝道岔区道床阻力、间隔铁阻力以及导轨与基本轨相互作用的非线性关系[1-2]。为了研究桥上无缝道岔的受力和变形,本文从整个线桥系统出发,基于非线性有限单元法建立道岔—桥梁的一体化模型,以郑西客运专线渭南北站两端咽喉区多跨连续梁桥及变宽度连续梁桥桥上无缝道岔区为例,研究在温度场作用下无缝道岔与桥梁的相互作用机理。
郑西客运专线为双线铁路,其中渭南段内的潼关、华阴区间地形多样、地质复杂,铁路、公路、电力、通信线路交跨十分频繁。为充分利用桥梁下部空间、节约用地,渭南北站站房设置于铁路桥梁下方,车站两端咽喉区分别位于大桥变宽度连续梁桥上。桥上铺设18号高速道岔。
1 桥上无缝道岔空间耦合计算模型
本文采用通用空间有限元分析软件MIDAS/CIVIL建立渭南北站桥上5#和7#岔位、1#和3#岔位的无缝道岔—桥梁有限元模型。
1.1 计算参数
根据渭南桥及桥上无缝道岔总体设计单位提供的设计资料,确定如下计算参数。
(1)钢轨温升43 ℃,桥梁温升20 ℃;
(2)1#和3#岔位为18号渡线道岔,5#和7#岔位为18号单开道岔;
(3)1#和3#岔位的渡线道岔所在连续梁为(30+48+56+48+30)m无砟混凝土连续梁,西安端温度跨为134 m,郑州端温度跨为78 m;
(4)5#和7#岔位的单开道岔所在连续梁为(30.7+48+33)m变宽度连续梁;
(5)道岔全长69 m,前长31.729 m,后长37.271 m,导曲线半径为1 100 m,尖轨长22.090 m;
(6)轨下基础为无砟道床,岔枕为德国高铁设计的雷达2000岔枕,无砟岔枕的类型为GWS05—300W型。
1.2 基本假定
(1)由于渭南桥上无缝道岔的尖轨跟部未设置间隔铁或限位器,因此假定尖轨尖端的纵向位移由辙叉区纵向位移和尖轨本身自由伸缩位移组成。
(2)由于渭南桥上无缝道岔直接安装在长枕埋入式无砟轨道上,且辙叉范围约为10 m,间隔铁的纵向刚度可以近似认为无穷大,因此将辙叉区间隔铁等部件模拟为刚体约束[8]。
(3)在计算温差引起的岔梁纵向相互作用时,计算1次升温(或降温)到某一温差值,而不考虑实际升降温的交替循环过程。
(4) 道岔区轨下铁垫板与轨枕或支承块为刚性连接,轨枕或支承块与轨道板为刚性连接,轨道板与梁面也为刚性连接。
(5)桥梁固定支座没有间隙,活动支座的纵向移动时考虑一定的摩擦系数。
1.3 计算模型
按实际的外形尺寸建立5#,7#岔位和1#,3#岔位的梁轨相互作用计算模型。道岔区钢轨按支承节点划分单元,采用三维梁单元模拟,不考虑轨道板及砂浆层的纵向弹性,钢轨与桥面之间采用3个方向的弹性连接[3-6]。轨道的垂向刚度主要由轨下胶垫提供,数值取为60 kN·mm-1;横向刚度根据实测数据确定,参考北京交通大学的岔区钢轨横向位移计算结果[7],第1阶段的切线刚度取为150 kN·mm-1;纵向刚度主要由扣件的纵向阻力提供,取为15 kN·m-1。
由于钢轨断面远小于桥梁断面,如对桥梁采用空间梁单元建模,将会使钢轨与桥梁间相对伸缩产生的荷载作用于整个桥梁截面上,这与实际情况存在明显不符。因此,为准确分析钢轨与桥梁的空间相互作用,对桥梁梁体结构采用空间板壳单元建模;另外,横隔板因较厚,将其处理成相应长度范围内的3层板,以满足板壳元的基本假定条件。
桥梁采用盆式橡胶支座,固定支座无纵向位移,活动支座的理论摩擦系数为0.03,也就是最大纵向力为垂向支反力的3%,但考虑到梁部结构较重,而线路温升产生的支座纵向反力达不到垂向支反力的3%,因此认为活动支座与固定支座类似,梁、墩间无纵向相对位移,模型中的弹性约束条件反映的是桥墩结构的纵向刚度,由设计资料直接给定。
为了反映梁端以外扣件、垫板等对钢轨伸缩变形的影响,对关注的连续梁梁端各3跨简支梁也进行了仿真建模,作为一个线路整体进行计算分析,计算模型如图1和图2所示。

图1 5#和7#岔位单开道岔—桥梁计算模型
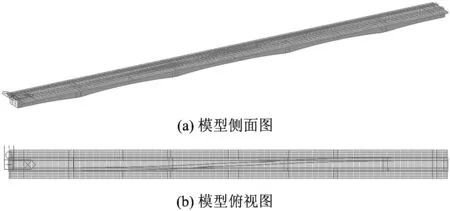
图2 1#和3#岔位渡线道岔—桥梁计算模型
2 计算结果与分析
2.1 桥梁梁体变形
5#和7#岔位单开道岔区桥梁梁体纵、横向位移云图如图3和图4所示,1#和3#岔位渡线道岔区桥梁梁体纵、横向位移云图如图5和图6所示。

图3 5#和7#岔位道岔区桥梁梁体纵向位移云图
由图3—图6的仿真计算结果,统计得出不同岔位处连续梁梁体的纵向、横向位移最大值以及发生位置,见表1。

图4 5#和7#岔位单开道岔区桥梁梁体横向位移云图

图5 3#和1#岔位道岔区桥梁梁体纵向位移云图

图6 3#和1#岔位道岔区桥梁梁体横向位移云图

岔位方向最大值/mm最大值位置5#和7#横向27梁体外侧5#和7#纵向53梁端 3#和1#横向28梁体外侧3#和1#纵向268梁端
由表1可以看出:无论是单开道岔还是渡线道岔,梁体横向位移最大值都非常接近且数值较小,由于计算过程中考虑了道岔区钢轨升温以及桥梁升温两者的组合情况,所得数值为桥梁绝对变形,数值小说明道岔区钢轨变形对桥梁横向位移影响较小,桥梁横向位移主要由梁体均匀温升引起,且整个桥梁长度方向对应的节点横向变形应该较为一致,发生位置均为梁体横向的一侧;梁体最大纵向位移发生的位置均在梁端部,但单开道岔区的梁体最大纵向位移较小,渡线道岔区的梁体纵向位移较大。
2.2 道岔区钢轨变形
图7—图10分别给出了5#和7#岔位单开道岔直股、曲股钢轨的最大横向和纵向位移。

图7 5#和7#岔位单开道岔直股钢轨的最大横向位移
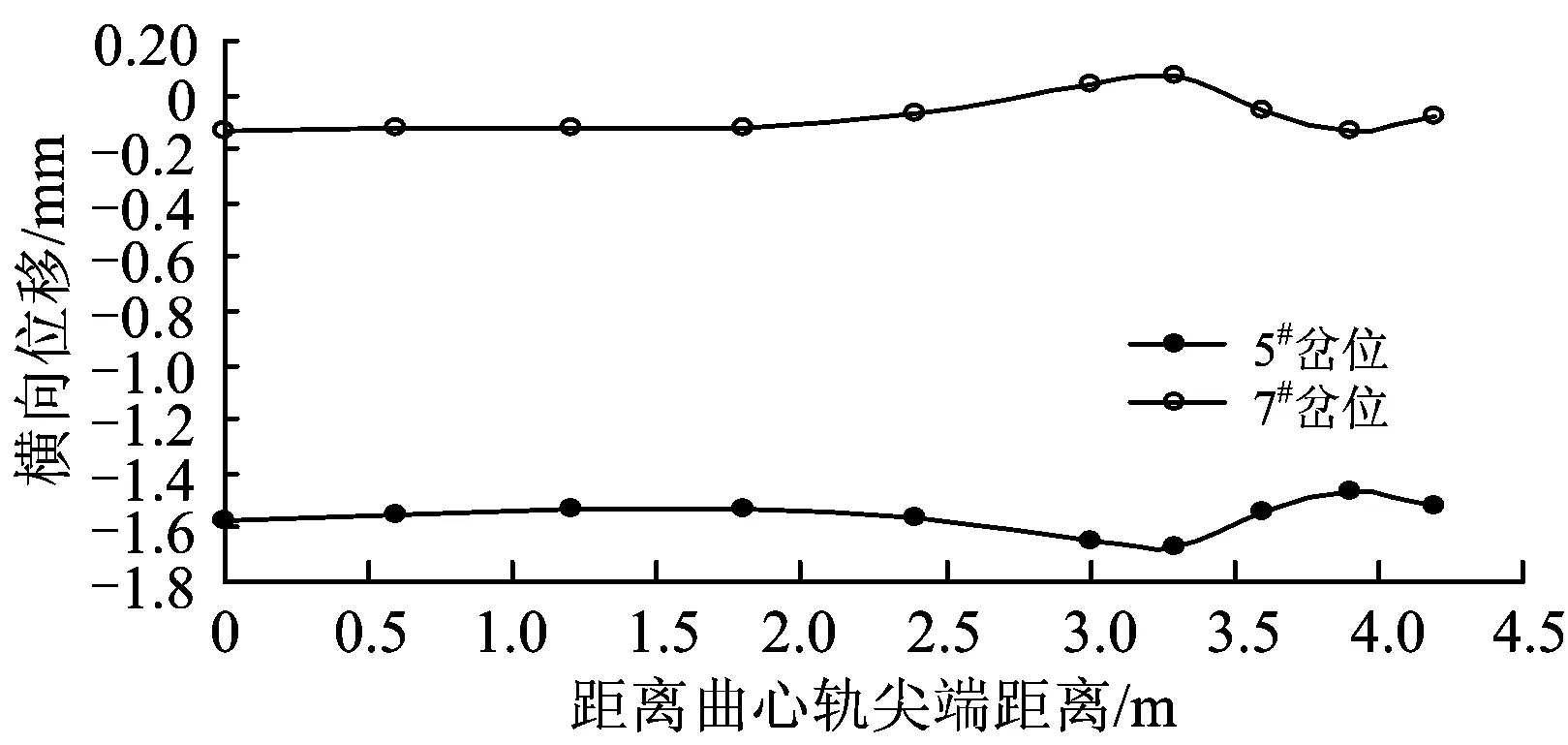
图8 5#和7#岔位单开道岔曲股钢轨的最大横向位移

图9 5#和7#岔位单开道岔直股钢轨的最大纵向位移

图10 5#和7#岔位单开道岔曲股钢轨的最大纵向位移
由图7和图8可以看出:单开道岔直股、曲股钢轨的最大横向位移分别发生在直尖轨和曲心轨处,直股的最大横向位移为1.28 mm、曲股的最大横向位移为1.67 mm。由图9和图10可以看出:直股、曲股钢轨的最大纵向位移均发生在尖轨尖端,直股的最大纵向位移为23.13 mm、曲股的最大纵向位移为25.22 mm。
图11—图14给出了1#和3#岔位渡线道岔直股、曲股钢轨的最大横向和纵向位移。
由图11和图12可以看出,渡线道岔直股、曲股钢轨的最大横向位移分别发生在直心轨和曲尖轨处,直股的最大横向位移为1.12 mm、曲股的最大横向位移为1.49 mm。由图13和图14可以看出。渡线道岔直、曲股钢轨的最大纵向位移分别发生在直尖轨尖端和曲尖轨尖端,直股的最大纵向位移为21.51 mm、曲股的最大纵向位移为28.14 mm。

图11 1#和3#岔位渡线道岔直股钢轨的最大横向位移

图12 1#和3#岔位渡线道岔曲股钢轨的最大横向位移

图13 1#和3#岔位渡线道岔直股钢轨的最大纵向位移
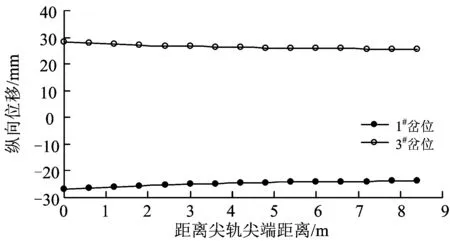
图14 1#和3#岔位渡线道岔曲股钢轨的最大纵向位移
表2给出了单开道岔和渡线道岔钢轨的横移、纵移最大值及发生位置。

表2 不同岔位道岔钢轨位移的最大值及发生位置
由表2可见,无论是单开道岔还是渡线道岔,钢轨的纵向位移远大于横向位移,但数值均小于钢轨位移允许值40 mm,且富余量较大;单开道岔和渡线道岔的最大钢轨纵向和横向位移在数值上非常接近,均发生在曲股,说明道岔结构类型对温度变形的影响可以忽略不计。结合2.1节的计算结果可以认为,5#和7#岔位和3#和1#岔位处桥梁梁体纵向位移的差异主要是由桥梁结构本身的差异造成的(5#和7#岔位处桥梁为变宽度梁),而与道岔结构类型无关。因此对于桥梁的养护维修,可不必过于关注道岔温度力的影响。
2.3 道岔区钢轨纵向力
在梁体和道岔区钢轨随温度变化产生伸缩的作用下,桥梁梁体和轨道之间产生相对位移,钢轨产生纵向附加力,对桥面系作用大小相等、方向相反的反作用力,此力通过梁、支座传递至墩台,在钢轨与桥梁之间形成1个纵向相互作用的力学平衡体系。道岔—桥梁的相互作用,一方面是由于梁体随温度变化产生伸缩引起桥梁与道岔的相互作用;另一方面是道岔区钢轨由于温度变化引起的伸缩通过扣件传递给桥面系,引起道岔与桥梁的相互作用。钢轨纵向力应由钢轨温升引起的温度力以及桥梁伸缩引起的附加力叠加组成。
仿真计算得出的各岔位道岔钢轨纵向力的最大值及发生位置见表3,纵向力分布云图如图15—图16所示。

表3 不同岔位道岔钢轨纵向力的最大值及发生位置
由图15、图16和表3可知:无论是单开道岔还是渡线道岔,最大钢轨纵向力均发生在连续梁梁缝附近约20 m范围内,单开道岔的最大纵向力为1 303.6 kN,其中温度力为849 kN、梁轨伸缩力为454 kN;渡线道岔的最大纵向力为1 340 kN,其中温度力为864 kN、梁轨伸缩力为476 kN。因此对道岔区梁体左右梁缝处的无缝线路应加强监测和养护,防止夏季出现胀轨、冬季出现断轨,且建议在梁缝处适当减小扣件阻力。

图15 5#和7#岔位单开道岔钢轨的纵向力分布云图

图16 3#和1#岔位渡线道岔钢轨的纵向力分布云图
3 结 论
(1)在温度荷载作用下,单开道岔和渡线道岔钢轨的纵向位移远大于横向位移,钢轨最大横向位移都在1~2 mm,最大纵向位移都在20~30 mm,但两者均小于钢轨位移允许值40 mm,且富余量较大。
(2) 单开道岔和渡线道岔钢轨的最大纵向温度力分别为1 303和1 340 kN,均发生在连续梁梁缝附近约20 m范围内,因此对梁体左右梁缝处的无缝线路应加强监测和养护,防止夏季出现胀轨、冬季出现断轨现象,且建议在梁缝处适当减小扣件阻力。
(3)单开道岔和渡线道岔区桥梁梁体最大横向位移分别为2.7和2.8 mm,两者数值非常接近且均较小,由于计算过程中考虑的是道岔钢轨升温以及桥梁梁体升温两者的组合情况,所得数值为桥梁绝对变形,数值小说明道岔钢轨变形对桥梁横向位移影响较小,可以不考虑钢轨变形的影响,因此桥梁梁体横向变形主要由梁体均匀温升引起。
(4)单开道岔和渡线道岔区桥梁梁体最大纵向位移均发生在梁端部,分别为5.3和26.8 mm,前者较小,后者较大,这主要是由桥梁结构本身的差异造成的,与道岔结构类型无关。因此对于桥梁的养护维修,可不必过于关注道岔区温度力的影响。
[1]马战国, 郝有生, 王红. 秦沈客运专线38号无缝道岔纵向力分析及试验研究[J]. 中国铁道科学, 2002,23(2):71-74.
(MA Zhanguo,HAO Yousheng, WANG Hong. The Analysis and Research of Longitudinal Force of No.38 Turnout Connected with CWR Rails on Qin-Shen Railway[J]. China Railway Science, 2002,23(2):71-74. in Chinese)
[2]张世杰.桥上无缝道岔交叉渡线无砟轨道影响因素分析[J]. 铁道工程学报, 2013(10):48-54.
(ZHANG Shijie. Analysis of Influence Factors for the Seamless Turnout Scissors Crossing Ballastless Track on Bridge[J]. Journal of Railway Engineering Socity,2013(10):48-54. in Chinese)
[3]王树国,林吉生.大号码无缝道岔温度力与变形的有限元计算[J].中国铁道科学,2005,26(3):68-72.
(WANG Shuguo,LIN Jisheng. Analysis on the Temperature Stress and Deformation of Large-Size Continuously Welded Turnout by Finite Element Program[J]. China Railway Science, 2005,26(3):68-72. in Chinese)
[4]孙大新, 高亮, 刘衍峰. 桥上无碴轨道无缝道岔力学特性分析[J]. 北京交通大学学报, 2007,31(1):89-92.
(SUN Daxin, GAO Liang, LIU Yanfeng. Analysis of Mechanical Characteristics to the Jointless Switch on Ballastless Bridge[J]. Journal of Beijing Jiaotong University, 2007,31(1):89-92. in Chinese)
[5]刘衍峰, 高亮, 冯雅薇. 桥上无缝道岔受力与变形的有限元分析[J]. 北京交通大学学报, 2006,30(1):66-70.
(LIU Yanfeng, GAO Liang, FENG Yawei. Finite Element Analysis of Jointless Turnout on Bridge[J]. Journal of Beijing Jiaotong University, 2006,30(1):66-70. in Chinese)
[6]徐桂弘, 徐浩, 王平,等. 无碴轨道连续梁桥与道岔纵向相互作用规律的研究[J]. 铁道建筑, 2011(5): 119-123.
(XU Guihong, XU Hao, WANG Ping, et al. Longitudinal Interaction Study of Ballastless Continuous Bridge and Turnout[J]. Railway Engineering, 2011(5): 119-123. in Chinese)
[7]中国铁道科学研究院. 郑西客运专线新渭南站桥上无缝道岔试验研究[R]. 北京:中国铁道科学研究院, 2010:48-59.
