基于赫兹接触的钢轨砂带打磨功率预测模型

王文玺，李建勇,2，樊文刚,2，刘月明,2

(1.北京交通大学 机械与电子控制工程学院，北京　100044；2.北京交通大学 载运工具先进制造与测控技术教育部重点实验室，北京　100044)

在钢轨使用中，动态载荷反复作用会引发其内部和表面的损伤，包括波浪形磨耗、灼伤、剥离、掉块及压溃等，因此需要采取主动性的处理机制——钢轨打磨[1-4]。近年来，高铁已成为我国国民经济发展、国家安全保障的重要战略支撑。截至2016年，我国高铁总里程已突破2万km，高铁规模稳居世界第一。可是，由于高铁客流逐年递增、而“天窗”维修时间[4]却逐年减少，使得高铁线路的养护需求日益迫切，面临的挑战越加严峻。目前，主流的钢轨打磨方式以砂轮打磨为主，钢轨铣磨为辅[1-4]。由于砂轮自身的刚性特点，打磨时易发生破碎和磨损，进而会对轨面造成二次损害，因此，其实际打磨能力和运用范围受到了极大限制。相比之下，砂带打磨作为“万能”加工方式，还具有冷态磨削、弹性磨削、高效磨削等优点，可以预见，采用新型砂带打磨方式进行线路养护作业将能有效应对作业高效化、智能化及多样化的挑战[4]。

在钢轨打磨中，打磨功率是3大关键参量之一，打磨功率直接控制打磨深度进而决定修整后的轨面廓形[5]。针对钢轨的传统砂轮打磨，聂蒙[5]开展了打磨功率控制方法与打磨温度建模的相关研究；智少丹等[6-7]从磨粒磨削机理开展了打磨功率对打磨深度和打磨模式的影响分析。本文根据钢轨砂带打磨中曲面接触及弹性接触的特点，分析打磨过程中接触区域的状态，推导接触压力与磨粒切深间的关系，建立钢轨砂带打磨功率预测模型，并借助钢轨打磨试验台对预测模型进行验证；以60 kg·m-1钢轨砂带打磨为例，仿真分析打磨功率与砂带速度的配比关系。

1　钢轨砂带打磨装置的结构及作业过程

单接触轮式钢轨砂带打磨装置的结构如图1所示。图中：x方向为接触轮轴向，y方向为轨向，z方向为轨顶法向。砂带磨头结构由接触轮和外包砂带构成，接触轮则包含内部刚性轮芯和外部弹性橡胶层。接触轮在气缸压力Fg驱动下，使砂带与钢轨表面接触并形成接触压力Fn。打磨列车以速度vf沿轨道行驶，同时砂带在张紧力F1和F2作用下，以线速度vb沿同方向磨削钢轨表面。因钢轨廓形截面由多段圆弧组成，且沿钢轨轴向又存在波浪形磨耗，故可将此种接触状态视为2个自由曲面接触。

图1　单接触轮式钢轨砂带打磨装置结构

2　砂带—钢轨接触模型

弹性赫兹接触理论表明，2个自由曲面的接触区域形状成椭圆形，其上的法向压力分布则呈半椭球形[8-9]，如图2所示。图中：a和b分别为椭圆形接触区域的长、短半轴。

图2　打磨过程中磨削区域压力分布

根据图2，建立砂带—钢轨接触模型为

(1)

其中，

κs=κ11+κ12+κ21+κ22

E12=10exp(0.019 8Hs-0.543 2)

式中：ma和mb分别为与椭圆离心率相关的中间变量；κs为接触轮和钢轨表面的主曲率之和；υ1和υ2分别为橡胶和钢轨的泊松比；E1和E2分别为接触轮和钢轨的弹性模量；e为椭圆离心率；L(e)为第二类椭圆积分；g为接触区域长短轴之比；κ11和κ12为接触轮2正交方向主曲率；κ21和κ22为钢轨2正交方向主曲率；E11和E12分别为接触轮毂和橡胶的弹性模量；δ11和δ12分别为轮毂和橡胶层的厚度；Hs为橡胶的邵氏硬度。

在接触问题中，主曲率函数f(κ)为

f(κ)=[(κ11-κ12)2+2(κ11-κ12)(κ21-

(2)

式中：ω为钢轨与接触轮主平面间夹角。

主曲率函数f(κ)还可表示为接触区域长短轴之比g的函数，为

(3)

其中，

式中：K(e)为第一类椭圆积分。

根据式(2)和式(3)，可求解出接触区域长短轴之比g。

椭圆接触区域上的法向压力分布p(x,y)为

(4)

3　打磨功率预测模型

3.1　基本假设及简化

砂带通常采用“静电植砂”工艺将针状磨粒均匀植在砂带表面。因植砂过程中磨粒出现尖端放电效应，使得绝大部分磨粒刃尖朝上。因为球顶圆锥模型相对其他简化模型更符合实际划擦沟槽形状和磨粒划擦受力情况[8]，所以将砂带表面的磨粒层看作由大量均匀分布、具有相似外形而高度各异的球顶圆锥体组成。简化的球顶圆锥体模型如图3所示。图中：r为磨粒刃端半径；θ为磨粒半顶锥角；h为磨粒出刃高度。

图3　简化的球顶圆锥体模型

而磨粒的刃端半径均值为ra，半顶锥角均值为θa，它们可通过标准ISO 25178-2—2012 中的三维表面特征参数Sdq(均方根倾斜度)和Spc(算术平均波峰曲率)推算[10]，分别为

(5)

(6)

因砂带表面磨粒的高度参差不齐，假设砂带表面磨粒的高度服从正态分布，则磨粒出刃高度分布的概率密度函数f(h)[11]为

(7)

式中：σ为磨粒出刃高度的均方差。

3.2　打磨功率

随切入深度δ的增加，砂带表面的磨粒经历弹性、弹—塑性和塑性变形3个阶段。当δ小于临界切深δ1时，钢轨表面为完全弹性变形；当切深大于临界切深δ2时，钢轨表面为完全塑性变形；当δ1<δ<δ2时，工件表面变形介于弹性和塑性之间。

弹—塑性变形起始于平均压力pmean=HB/3时(HB为钢轨的布氏硬度)，此时临界切深δ1为[12]

(8)

其中，

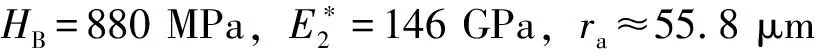
砂带表面磨粒与钢轨表面干涉磨粒的概率分布如图4所示。图中：以磨粒出刃高度均值对应的位置为原点，在砂带表面建立直角坐标系；δmax为最高磨粒切削时对应的最大切入深度；hmin为砂带表面磨粒最低高度；h0为钢轨轨面与砂带坐标系原点的距离，h0=3σ-δmax。

图4　砂带磨粒与钢轨表面干涉磨粒的概率分布图

由图4可见，磨粒切入深度δ=h-h0；随最大磨粒切入深度δmax的变化，有效切削磨粒数将随之变化。

当磨粒切入深度δ≤ra(1-cosβ)(β=90°-θ)时，磨粒只有球顶部分切入钢轨表面，单颗磨粒所受的法向力Fp和切向力Ft[14]分别为

(9)

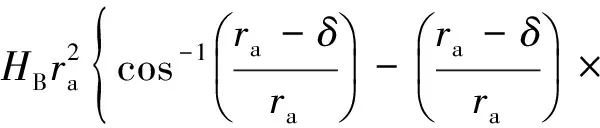
(10)

当磨粒切入深度δ>ra(1-cosβ)时，磨粒圆锥部分亦切入钢轨表面，此时单颗磨粒所受法向力Fp和切向力Ft[14]分别为

sin2β}

(11)

(12)

在接触区域内某一坐标(x，y)处微元内，其磨粒最大切入深度为δmax(x，y)， 则对应的法向压强pp(x，y)和切向压强pt(x，y)分别为

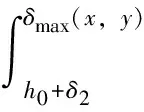
(13)

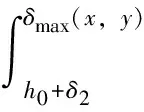
(14)

式中：ρ为砂带表面磨粒植砂密度。

联立式(4)和式(13)，由数值积分可求得δmax(x，y)，进而由式(14)求得pt(x，y)。则接触区域砂带表面微元面积dxdy上磨粒形成的打磨功率dP为

dP=vbPt(x,y)dxdy

(15)

则整个椭圆接触区域所形成的打磨功率P为

(16)

4　模型验证及打磨功率的作用分析

4.1　模型验证

图5为研发的“钢轨砂带打磨综合试验平台”，试验台钢轨调速范围为1～30 km·h-1，砂带调速范围为1～60 m·s-1，打磨压力调整范围为100～7 000 N，张紧压力调整范围为100～4 000 N。综合试验平台能够测量打磨功率、接触压力、钢轨扭矩等20项参数。

图5　钢轨砂带打磨综合试验平台

受试验场地限制，试验台选用环形钢轨进行回转运动以模拟线上打磨作业。选用3M公司36+号陶瓷磨料砂带对U71Mn材质钢轨圆环进行打磨试验。试验中已知参数见表1。

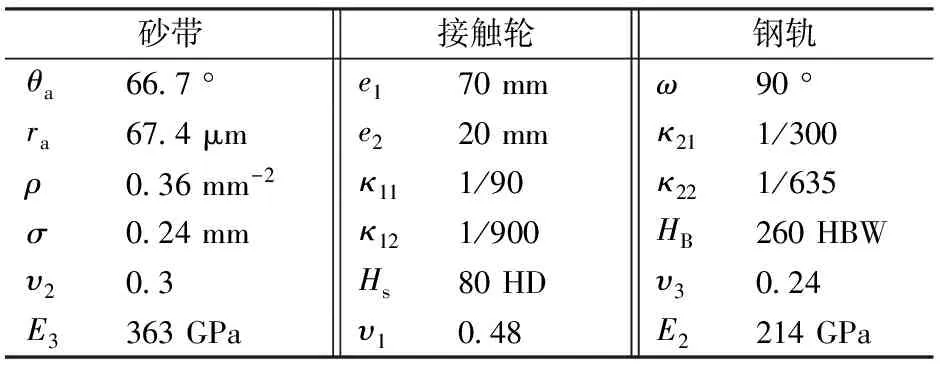
表1　预测模型所需参数

由预测模型得到的预测值与试验值的对比见表2。表中：砂带1主要验证不同打磨作业参数下的打磨功率，而砂带2主要验证某一工艺参数下全寿命周期中的打磨功率。

表2　打磨功率预测模型的预测值与试验值的对比

由表2可知，打磨功率随接触压力和砂带速度的增加而增加；打磨功率的试验值和预测值最大偏差为3.85%，偏差均值为2.03%，波动范围为-3.85%～2.99%，表明预测值与试验值有较好的一致性，证明该预测模型是有效的。

4.2　打磨功率的作用分析

打磨作业过程中，行车速度、砂带种类、磨头尺寸及橡胶硬度等参数通常是选定后不变的，只可通过接触压力和砂带速度调节打磨状态。虽然打磨深度与接触压力Fn密切相关，但在实际打磨中Fn由Fg，F1，F2以及F1，F2与Fg间的夹角等参数决定，其中仅Fg较易监测，因此利用打磨功率对打磨状态进行监控和调节是一种更为普遍的控制方式[6]。

以60 kg·m-1钢轨为例，钢轨廓形由曲率半径R为300，80和13 mm这3种圆弧组成。采用预测模型对不同曲率弧段的打磨功率与砂带速度配比进行数值仿真分析，结果如图6所示。

图660 kg·m-1钢轨各弧段打磨功率与砂带速度配比的关系

从图6可知：在同一砂带速度和同一接触宽度下，R300弧段对应的打磨功率(打磨深度)最低，而R13弧段对应的打磨功率(打磨深度)最高；在同样的打磨功率下，对于R300弧段能够调整的打磨宽度范围最广，R80弧段次之，R13弧段最窄，且变化趋势呈非线性；此外，接触宽度虽然由接触压力直接决定，但同时还会受到打磨功率的制约，进而限制对砂带速度的调节；若要实现全轨廓覆盖打磨，须根据既定的砂带速度和打磨功率，合理布置磨头的数量和位置，优化打磨列车的设计和打磨方案。

5　结　语

(1)在阐述钢轨砂带打磨原理的基础上，利用弹性赫兹接触理论分析了接触轮与钢轨轨面的接触状态，得到了打磨压力与磨粒切入深度间的数学关系。

(2)从单磨粒切削过程中的受力出发，建立钢轨砂带打磨功率的预测模型，验证了模型预测值与试验结果吻合，证明了预测模型模型的有效性和适用性。

(3)以60 kg·m-1钢轨为例，采用预测模型分析了在不同打磨位置时打磨功率与砂带速度配比关系对打磨宽度的影响。结果表明：R300弧段打磨宽度可调整范围最大，而R13弧段最小；在实际打磨中除了获得指定接触压力外还须考虑打磨功率对打磨宽度的限制。

[1]金学松, 杜星, 郭俊,等. 钢轨打磨技术研究进展[J]. 西南交通大学学报, 2010, 45(1):1-11.

(JIN Xuesong, DU Xing, GUO Jun, et al. State of Arts of Research on Rail Grinding[J]. Journal of Southwest Jiaotong University, 2010, 45(1):1-11. in Chinese)

[2]ZHI Shaodan, LI Jianyong, ZAREMBSKI A M. Grinding Motor Energy Saving Method Based on Material Removal Model in Rail Grinding Processes[J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2015, 2(1): 21-30.

[3]ZHI Shaodan, ZAREMBSKI A M, LI Jianyong, et al. Towards a Better Understanding of the Rail Grinding Mechanism[C]//ASME 2013 Rail Transportation Division Fall Technical Conference. Altoona: American Society of Mechanical Engineers, Rail Transportation Division RTD, 2013:15-17.

[4]刘月明, 李建勇, 蔡永林,等. 钢轨打磨技术现状和发展趋势[J]. 中国铁道科学, 2014, 35(4):29-37.

(LIU Yueming, LI Jianyong, CAI Yonglin, et al. Current State and Development Trend of Rail Grinding Technology[J]. China Railway Science, 2014, 35(4):29-37. in Chinese)

[5]聂蒙. 基于变参数气动结构的钢轨打磨恒功率控制技术研究[D]. 北京：北京交通大学, 2015.

(NIE Meng. Research on Constant-Power Control Technology for Rail Grinding Based on Variable Parameter Pneumatic Structure[D]. Beijing: Beijing Jiaotong University, 2015. in Chinese)

[6]智少丹, 李建勇, 刘月明,等. 基于磨粒切削模型的钢轨打磨机理研究[J]. 中国铁道科学, 2015, 36(1):33-39.

(ZHI Shaodan, LI Jianyong, LIU Yueming, et al. Rail Grinding Mechanism Based on Grain Cutting Model[J]. China Railway Science, 2015, 36(1):33-39. in Chinese)

[7]ZHI Shaodan, LI Jianyong, ZAREMBSKI A M. Predictive Modeling of the Rail Grinding Process Using a Distributed Cutting Grain Approach[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016, 230(6): 1540-1560.

[8]言兰, 融亦鸣, 姜峰. 氧化铝砂轮地貌的量化评价及数学建模[J]. 机械工程学报, 2011, 47(17):179-186.

(YAN Lan, RONG Yiming, JIANG Feng. Quantitive Evaluation and Modeling of Alumina Grinding Wheel Surface Topography[J]. Journal of Mechanical Engineering, 2011, 47(17):179-186. in Chinses)

[9]温诗铸. 摩擦学原理[M].北京: 清华大学出版社, 1990:125-164.

[10]ZHAO Y, MAIETTA D M, CHANG L. An Asperity Microcontact Model Incorporating the Transition from Elastic Deformation to Fully Plastic Flow[J]. Journal of Tribology, 2000, 122(1):86-93.

[11]王文玺, 李建勇, 樊文刚,等. 面向钢轨砂带打磨的砂带磨耗过程建模[J]. 西南交通大学学报, 2017, 52(1):141-147.

(WANG Wenxi, LI Jianyong, FAN Wengang, et al. Abrasion Process Modeling of Abrasive Belt Grinding in Rail Maintenance[J]. Journal of Southwest Jiaotong University, 2017, 52(1):141-147. in Chinese)

[12]JOURANI A, HAGEGE B, BOUVIER S, et al. Influence of Abrasive Grain Geometry on Friction Coefficient and Wear Rate in Belt Finishing[J]. Tribology International, 2013, 59:30-37.