基于刚体模型的铁道车辆曲线运动轮轨力分析

金　刚，时　瑾

(1.周口师范学院 机械与电气工程学院，河南 周口　466001；2.北京交通大学 土木建筑工程学院，北京　100044)

铁路线路曲线地段是线路的薄弱环节[1]。曲线的线型及参数设置不仅影响列车运行的乘坐舒适性和安全性，而且还与线路曲线地段的轮轨蠕滑力和法向力造成的轨道病害[2-3]密切相关。因此，线路曲线线型和参数始终是铁路线路设计理论研究的重点[4]。

车辆通过曲线时的动力学作用机制较为复杂[5]，轨道弹性变形、轨道不平顺及车轮损伤等都会影响曲线地段车辆与轨道的动力相互作用。国内外学者针对这一问题提出了诸多模型[6-7]。这些模型均将车辆视为多自由度系统或刚柔体弹性系统，并考虑轨道结构、路基及桥梁的振动特性。轮轨间相互作用力的分析常采用赫兹弹性接触理论和Kalker蠕滑理论实现[8-9]。这类模型一般用于研究结构振动、部件可靠性等问题。车辆曲线运动造成的动力学行为的特征主要表现为低频振动，这类动力学行为与线路参数密切相关。在铁路设计规范中，线型及曲线参数的确定一般采用刚体受力分析，以未被平衡加速度作为控制指标，得到线路参数的取值和匹配条件。需要说明的是，由于车辆在线路曲线段同时具有点头、摇头和侧滚运动，运动形态复杂，但在已有的车辆刚体模型中并未考虑曲线段轮轨作用力特性，因而也导致了线路参数选取中不能全面考虑线路设置对运营的影响。长期以来，曲线段的轮轨力大都需要借助车轨动力学计算得到，计算工作量大。到目前为止，尚未见表述车辆在曲线段整体运动的动力学方程。本文旨在完善发展刚体动力学模型，以期实现对轮轨力、舒适性的高效预测，为铁路线路线型及参数分析提供一种新的简便方法。

一般情况下，铁路曲线由圆曲线和缓和曲线连接而成，其线型研究的核心是缓和曲线。1865年法国人夏克建立三次抛物线型缓和曲线[10]，至今我国的普通铁路和高速铁路仍采用这种线型[11]。但理论上该缓和曲线与直线和圆曲线的连接点立面上切线不连续，会对线路的平顺性带来不利影响。为了改进三次抛物线型缓和曲线的缺陷，国内外学者设计了几十种各种形式的缓和曲线。现已问世的缓和曲线大致分为两类：一类是以放射螺线(又称回旋线)的各种近似曲线为平面曲线，以直线或改善的直线顺坡超高为立面曲线的传统缓和曲线；另一类是以三角函数或高次多项式为基础的新型缓和曲线。新型缓和曲线能很好地改善曲线起终点的行车条件，但缓和曲线长度更长，增加了工程施工、线形检测和维护的困难。传统缓和曲线虽然可以采用更短的长度，却不利于列车在缓和曲线起终点的平稳运行，降低旅客乘坐舒适度，恶化运营条件，增加运营维护费用。高速列车运行速度高，线路曲线线型对列车运行品质的影响尤为显著，在实践中新型缓和曲线正在逐步被采用[12]。我国未来高速铁路可能会达到更高速度，采用动力学性能更为优越的缓和曲线十分必要。本文建立一种可以根据曲线线型简便计算轮轨力的刚体动力学模型，从理论层面对车辆曲线运动的轮轨力学特性进行定量分析，具有重要理论意义和工程价值。

1　铁道车辆刚体模型的建立

1.1　车辆整体运动假设

铁道车辆系统主要由车体、转向架、轮对及其悬挂系统组成，车辆设计的基本要求在于满足对线路空间轨迹的跟随。从宏观上看，车辆整体跟随线路空间轨迹是车辆最根本、最基础的要求，轨道交通线型参数设计就是要保证车辆的圆顺跟随。因此，国内外规范中均采用刚体模型估算列车运行的乘坐舒适性，并以此作为线型参数选取的理论依据。因此本文将车辆系统整体视为刚体以满足线型分析的需求。

1.2　车辆曲线运动分析

铁路线路曲线一般由“缓和曲线—圆曲线—缓和曲线”组成。车辆在曲线上运动时会产生法向加速度，以车辆为参照系时，等效于车辆受到1个指向曲线外侧的惯性离心力。为平衡这一侧向力，通常将外侧轨道抬高(称超高)，或内侧轨道降低，使得惯性离心力与重力的合力垂直于两股钢轨所决定的平面(称轨顶面)。满足这一条件时称之为“平—立面动力学协调”。但是，超高的引入使得外侧轨道与原直线轨道不在同一水平面内。同时，车辆在直线轨道上不受侧向力，若直接进入圆曲线会突然受到一个侧向惯性离心力，给行车安全和乘坐舒适性带来极为不利的影响。为解决这一问题，在圆曲线两端引入立面高度和平面曲率都逐渐变化的过渡曲线，这就是所谓的“缓和曲线”。由此可见，缓和曲线是一条空间曲线，车辆进入曲线轨道后的整体运动为三维空间运动。

车辆进入缓和曲线后，车辆呈现侧滚、点头、摇头等多种运动姿态。在外侧轨道超高时，若以车辆与内侧轨道的接触点作为随动坐标系(只随车辆平动而不随其转动)的原点，则车辆在该非惯性坐标系中的运动可简化为绕原点的3自由度纯转动。

高速铁路线路的缓和曲线长度约为500～1 000 m，圆曲线半径约为7 000～10 000 m，最大超高限值约为150～200 mm[13]，据此计算，车辆在缓和曲线段的摇头和侧滚总角位移约为10-1rad量级，而点头总角位移约为10-4rad量级，因而可忽略车辆的点头运动。根据加速度限值，车辆在缓和曲线上运动时，超高加速度不得大于0.4 m·s-2，除以轨距1.5 m，得侧滚角加速度约为0.27 rad·s-2。而摇头角速度为

(1)

式中：Ψ为切线转角，即摇头角；l为弧长；k为铁路线路平曲线的曲率；y为平曲线的切线支距；v为车辆运行速度。

车辆的摇头角加速度为

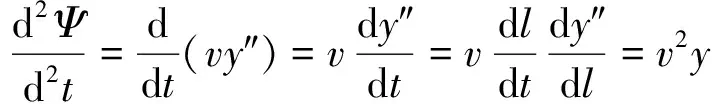
(2)

以我国铁路线路普遍采用的三次抛物线型缓和曲线为例，平面曲线为

y=l3/(6l0R)

(3)

式中：l0为缓和曲线长度；R为圆曲线曲率半径。

最大摇头角加速度出现在缓-圆点(缓和曲线与圆曲线的连接点)。取R=7 000 m，l0=700 m，v=100 m·s-1，代入式(2)，得最大摇头角加速度约为2×10-3rad·s-2，比侧滚角加速度小2个量级。车辆在其他类型缓和曲线上的摇头角加速度也有相同的量级。此外，前后轮对及车辆前后连接点对车辆质心的摇头力臂(约101m量级)比轮对的侧滚力臂(约100m量级)大1个量级，而车辆对质心的侧滚与摇头转动惯量具有同一量级[14]，故与车辆摇头运动有关的轮轨力至少要比引起侧滚运动的轮轨力小3个量级。再者，摇头力矩不单纯由前后轮对的侧向力提供，车辆前后的连接装置亦可提供，而侧滚力矩只能由轮对的垂向和横向轮轨力提供。由此可知，研究曲线段轮轨力时，可以忽略摇头的影响，仅考虑侧滚运动，将车辆简化为绕前进方向纵轴的一维转动刚体。

2　车辆刚体运动的动力学基本方程

2.1　任意超高设置下的动力学方程

任意超高时车辆的受力分析如图1所示。图中：F为轮对受到的轨道沿轨顶面的侧向力；F1为内侧(曲率中心一侧)车轮受到的垂直于轨顶面的正压力；F2为外侧轮受到的正压力；L为车辆质心C到内侧轮轨接触点A的距离；D为车辆质心C到轨顶面的距离；S为轨距；θ为轨顶面横坡角，亦为车辆所受重力与车辆竖向对称轴的夹角；φ为车辆质心到内侧轮轨接触点A的连线与车辆竖向对称轴的夹角；h为外轨超高；m为整车质量，亦可视为半车或1/4车质量，分别对应单轮对、单转向架或整车轮轨力；g为重力加速度。

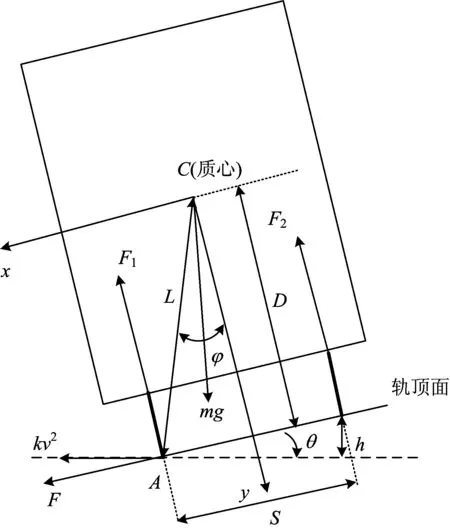
图1　任意超高时的车辆受力分析

以A为基点，质心的绝对加速度为

(4)

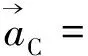
(5)

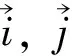
由质心运动定理可列出

(6)

mgcosθ-F1-F2=m(-kv2sinθ-

(7)

由对质心的动量矩定理可列出

(8)

式中：rc为车辆(亦可为整车、半车或1/4车)对质心的回转半径。

注意到：sinφ=S/(2L)，cosφ=D/L，故式(6)、式(7)和式(8)可改写为

(9)

2mgcosθ-2F1-2F2=

(10)

(11)

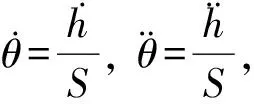
(12)

由此可解出任意超高下的轮轨力表达式

(13)

根据这一结果，只要知道平面曲线的曲率k、外轨超高h的表达式，以及车辆结构参数rc和D，轨距S和车辆运行速度v，即可计算出轮轨力。若曲线的超高完全按平—立面动力学协调关系设置，车辆基本动力学方程的建立和轮轨力求解还可进一步简化。

2.2　平衡超高下的动力学方程

平—立面动力学协调时，车辆的向心加速度完全由轨道正压力的水平分量提供。从车辆随动参照系看，惯性离心力与重力的合力垂直于轨顶面，作用于车辆质心C。以此作为平—立面动力学约束条件设置的曲线超高称“平衡超高”。设内轨水平高度不变，外轨超高，建立以内轨接触点为基点的随动参照系，车辆在曲线上的受力分析图如图2所示。图中，F0为车辆(或1/2、1/4车)所受的重力与平面曲线运动产生的惯性离心力的合力，作用于车辆质心C，在满足平—立面动力学协调关系的条件下，此力垂直于轨顶面。

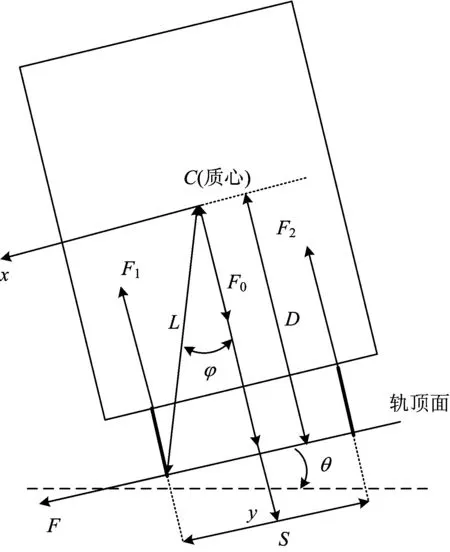
图2　平衡超高时车辆在曲线上的受力分析

根据质心运动定理和对质心的动量矩定理可列出动力学基本方程

(14)

解得

(15)

(16)

(17)

式(15)为车辆曲线运动轮轨力的精确解，式(16)和式(17)为轮轨力不同条件下的近似解，在车辆参数和速度一定的情况下，都可以通过超高h的表达式很方便地得到轮轨力。

上述2种情况下轮轨力的计算式都含有超高的二阶导数，因此超高的一阶导数必须连续(切线连续)。某些连续阶低的曲线(譬如3次抛物线型缓和曲线)理论上连接点立面上的切线不连续，不满足应用条件。但实际上钢轨的刚度总是有限值，在任何载荷和支撑下立面切线总是连续的，在计算时只需根据实际情况对连接点进行适当的圆顺即可。

3　应用实例

一波正弦型是部分国家高速铁路采用的缓和曲线线型，也是上海浦东磁悬浮线路采用的线型[15]。一波正弦缓和曲线平曲线的表达式为

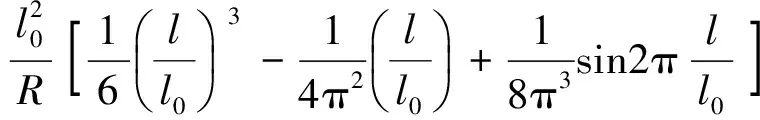
(18)

曲率表达式为

(19)

式中：k0为圆曲线曲率。

一波正弦缓和曲线的超高表达式为

(20)

式中：H为圆曲线实设超高。

本例取车辆运行速度v=100 m·s-1，圆曲线半径R=7 000 m，对应的平衡超高应为209 mm，圆曲线实设超高H=175 mm。取缓和曲线长度l0=630 m，轨距S=1.435 m，车辆参数D=1.77 m，rc=0.8 m，m=13.9 t(1/4车)。依据式(13)计算得到“一波正弦曲线630 m+圆曲线630 m+一波正弦曲线630 m”组合条件下的轮轨力如图3所示。

由图3可见：由于车辆处于欠超高状态，轮轨垂向力呈现内侧减载，外侧增载的特点，在圆曲线上轮轨垂向力增载和减载达到最大；轮轴横向力指向曲线内侧，由缓和曲线始点开始逐渐增大到圆曲线的最大值，为车辆曲线运动提供部分向心力，但增大了轮轨的磨损。

图3　刚体模型下计算的曲线轮轨力

车轨动力学考虑车辆部件振动、轮轨接触关系等列车运行时的动力学行为[9]。车轨动力学模型中将车辆简化为车体、前后构架和4个轮对组成的多刚体系统。车体、构架及轮对考虑浮沉、横移、侧滚、点头及摇头，轮轨几何关系采用接触迹线确定，采用经典的Kalker 滚动接触理论计算蠕滑力。图4为采用车轨动力学模型计算得到的轮轨垂向力和横向力。

由图4可见：由于车辆机构的约束关系和轮轨接触的作用，轮轨垂向力出现了一定程度的波动，但内外侧轮轨垂向力的变化趋势和图3(a)一致；由于转向架与轮对的约束关系，曲线通过时1位轮对和2位轮对的横向力差距较大，而两者的平均值则与图3(b)接近。

表1列出了2种模型计算得到的轮轨力结果。由表1可以看出，两者具有较好的一致性。因此，在工程设计中，由刚体动力学得出的式(13)可用于快速计算轮轨作用力。在平—立面动力学协调时，利用式(15)计算更为简单。式(16)和式(17)则可对轮轨力进行快捷估算。

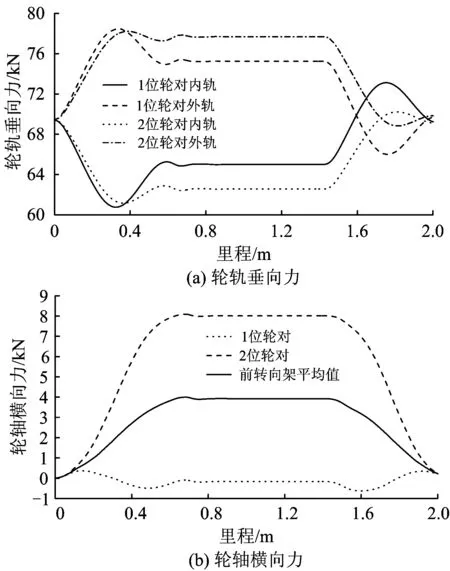
图4　车轨动力学模型计算的曲线轮轨力

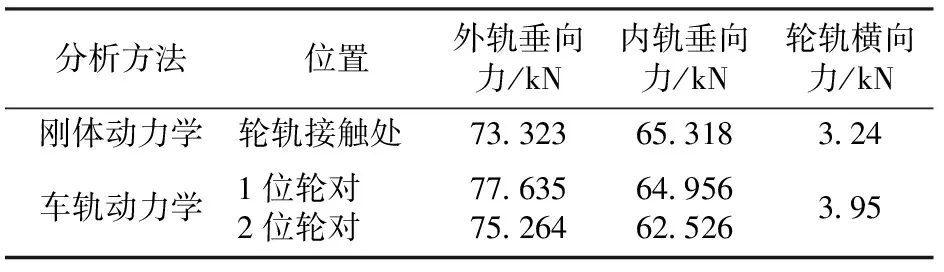
表1　采用2种模型计算的轮轨力结果

4　结　论

根据铁路线路和车辆特点，将车辆运动简化为绕纵轴的一维转动，建立考虑垂向、横向，侧滚运动的3自由度刚体模型。利用质心运动定理和对质心的动量矩定理，建立车辆动力学基本方程组，由此推导出任意超高、任意线型条件下轮轨力计算式及近似解，研究得到以下2点结论。

(1)铁路线路曲线地段轮轨力可由平面曲线的曲率k、外轨超高h的表达式、车辆质心到轨顶面距离rc、车辆对质心的回转半径D、轨距S和车辆运行速度v计算得出。

(2)结合高速铁路曲线线路条件，采用本文理论模型对曲线内外侧轮轨力变化情况进行了计算分析，内外侧轮轨垂向力和轮轴横向力变化规律与车轨动力仿真结果具有较好一致性。

本文研究提出的理论模型可方便高效地对铁道车辆曲线运动轮轨力实现预测，为铁路线路设计提供了一种新的方法。

[1]WANG Kaiyun, HUANG Chao,ZHAI Wanming, et al. Progress on Wheel-Rail Dynamic Performance of Railway Curve Negotiation[J]. Journal of Traffic and Transportation Engineering, 2014, 1(3): 209-220.

[2]王开云, 翟婉明, 刘建新, 等. 提速列车与曲线轨道的横向相互动力作用研究[J]. 中国铁道科学, 2005,26(6): 38-43.

(WANG Kaiyun, ZHAI Wanming, LIU Jianxin, et al. Research on the Lateral Dynamic Interaction between Speed-Increased Train and Curved Track[J]. China Railway Science, 2005, 26(6): 38-43.in Chinese)

[3]JABBAR A Z, VIDA G. Investigation on Dynamic Behavior of Railway Track in Transition Zone[J]. Journal of Mechanical Science and Technology, 2011, 25 (2): 287-292.

[4]KRZYSZTOF Zboiński. Dynamical Investigation of Railway Vehicles on a Curved Track[J]. European Journal of Mechanics-A/Solids, 1998, 17(6): 1001-1020.

[5]翟婉明. 车辆—轨道耦合动力学研究的新进展[J]. 中国铁道科学, 2002, 23(2): 1-14.

(ZHAI Wanming. New Advance in Vehicle-Track Coupling Dynamics[J]. China Railway Science, 2002, 23(2): 1-14. in Chinese)

[6]GIALLEONARDO E D, BRAGHIN F, BRUNI S. The Influence of Track Modeling Options on the Simulation of Rail Vehicle Dynamics[J]. Journal of Sound and Vibration, 2012, 331(19): 4246-4258.

[7]LUIS Baeza, OUYANG Huajiang. A Railway Track Dynamics Model Based on Modal Sub Structuring and a Cyclic Boundary Condition[J]. Journal of Sound and Vibration, 2011, 330: 75-86.

[8]杨久川, 王开云. 高速铁路平纵断面关键点处的轮轨振动特性[J]. 重庆理工大学学报：自然科学版, 2013, 27(9):49-52.

(YANG Jiuchuan, WANG Kaiyun. The Wheel-Rail Vibrations on the Key Points of Planar and Vertical Section in High-Speed Railways[J]. Journal of Chongqing University of Technology:Natural Science, 2013, 27(9): 49-52.in Chinese)

[9]龙许友,时瑾,王英杰. 高速铁路线路线形动力仿真及乘坐舒适度评价[J]. 铁道科学与工程学报, 2012(3): 26-33.

(LONG Xuyou, SHI Jin, WANG Yingjie. Dynamic Simulation and Ride Comfort Evaluation of Track Alignment for High Speed Railway[J]. Journal of Railway Science and Engineering, 2012(3): 26-33.in Chinese)

[10]吴耀庭. 铁路曲线及其养护[M]. 北京: 中国铁道出版社, 2001: 36-68.

(WU Yaoting. Railway Curve and Its Maintenance[M]. Beijing: China Railway Publishing House, 2001:36-38.in Chinese)

[11]国家铁路局. TB 10621—2014高速铁路设计规范[M]. 北京:中国铁道出版社, 2015:17-26.

(National Railway Administration of the People’s Republic of China. TB 10621—2014 Code for Design of High Speed Railway[M]. Beijing: China Railway Publishing, 2015: 17-26.in Chinese)

[12]LOUIS T Klauder, STEVEN M Chrismer, JOHN Elkins. Improved Spiral Geometry for High-Speed Rail and Predicted Vehicle Response[J]. Journal of the Transportation Research Board, 2002(1785): 41-49.

[13]白宝英. 高速铁路线路纵断面设计标准及其应用研究[J]. 铁道标准设计, 2010(7): 4-7.

(BAI Baoying. The Profile Design Standards and Their Application of the High-Speed Rail Line[J]. Railway Standard Design, 2010(7): 4-7. in Chinese)

[14]任尊松. 车辆系统动力学[M]. 北京: 中国铁道出版社, 2007: 187-188.

(REN Zunsong. Vehicle System Dynamics[M]. Beijing: China Railway Publishing House, 2007: 187-188.in Chinese)

[15]易思蓉. 上海磁悬浮示范运营线线路技术条件[J]. 中国铁路, 2001(8): 42-43.

(YI Sirong. Technical Condition of Magnetic Levitation Railway Demonstration Operation Line in Shanghai[J]. Chinese Railways, 2001(8): 42-43.in Chinese)