柔性轨道下高速列车车轮谐波磨耗对轮轨滚动接触蠕滑特性的影响

周新建，肖　乾,2,程　树，杨逸航

(1.华东交通大学 载运工具与装备教育部省部共建重点实验室，江西 南昌　330013；2.西南交通大学 牵引动力国家重点实验室，四川 成都　610031)

在车轮非圆化的问题中，谐波磨耗是最常见的形式之一。非圆化的车轮在轮轨高速运营中产生大幅度的轮轨垂向力波动，很大几率造成车轮与钢轨接触的瞬时脱离，引起另一侧轮对的轮轨垂向力发生变化[1]。车轮谐波磨耗导致高速轮轨接触的不平稳，恶化列车行车品质并引发轮轨间垂向/横向的高频振动以及振动带来的轮轨间瞬态高速冲击，对整个列车系统的安全性带来极大挑战[2]。

Johansson和Nielsen对轨道列车非圆化车轮与钢轨之间的接触垂向动态力以数值仿真和现场试验相结合的方法进行了详细分析[3]。张雪珊等人研究了考虑椭圆化车轮的列车横向稳定性问题[2]。黄江伟研究某型号地铁车辆车轮的多边形化带来的接触动力特性变化[4]。王亿佳等人把车轮非圆化考虑进车辆—轨道耦合大系统中，并结合实测多边形车轮和实验数据对车辆动力学新型进行对比运行研究分析[5]。宋颖采用大系统耦合动力学研究方法，建立车辆—轨道耦合模型，对非圆化高速列车轮轨接触间的相互作用力进行研究[6]。由此可见，国内外关于轮轨动力学的研究侧重点在车轮谐波磨耗对列车动力学特性的影响或基于车辆—轨道耦合的动力学分析，而很少深入考虑柔性轨道下因谐波磨耗车轮激励而引发钢轨和轮对振动时的轮轨蠕滑问题。

本文以实际常见的谐波磨耗车轮作为轮轨接触的谐波激扰源，建立柔性轨道的高速轮轨滚动接触动力学模型，分析谐波特性对高速轮轨滚动接触蠕滑特性的影响，进一步揭示谐波磨耗引发的轮轨滚动接触特性。

1　谐波磨耗特性和基于柔性轨道的轮轨蠕滑机理

谐波磨耗是由轮对制造误差或镟修下初始不圆造成的，表现为轮对的轴向不规则磨耗。可采用简谐波函数定义谐波磨耗车轮，即在车轮滚动1周内，将车辆圆周不圆顺的轮径差考虑为谐波函数[1]，有

(1)

式中：Δr为车轮圆周不圆顺的轮径差；A为不圆周不圆顺的幅值，即波深；n为车轮的谐波磨耗阶数，即谐波磨耗车轮在整个周长范围内形成的谐波函数周期；β为车轮转过的角度；β0为车轮转动的初始相位角；r(β)为车轮的实际滚动圆半径；r0为车轮的名义滚动圆半径；β(t)为车轮的圆周角；ω为车轮转动的角速度；Δt为时间的增量。

不同阶数的谐波磨耗车轮如图1所示。

由于轮对在实际运行中存在摇头角位移，使轮轨之间的接触点处于空间坐标系中，而不是处于轮轨间的主轮廓线上面。轮轨法向压缩量是表征轮轨垂向相对位移的重要参数，其在有轮轨垂向/横向振动和轨道不平顺时，受到轮轨的垂向相对位移和横移量、车轮的摇头角和侧滚角、钢轨的垂向和横向位移及扭转角等参数的影响[7]。

左、右侧轮轨的法向压缩量与轮对的垂向相对位移有关，可得

(2)

式中：L,R分别表示左、右车轮；Zi为轮轨的法向压缩量；φi为车轮踏面接触角；φW为轮对侧滚角；δZi为轮对的垂向相对位移。

对轮轨蠕滑率和蠕滑力进行分析时，采用Kalker非线性蠕滑理论以及沈志云-Hedrick-Elkins理论进行修正。考虑左、右钢轨垂向、横向和扭转振动速度的横、纵向轮轨蠕滑率ξc[7]为

(3)

其中，

式中：x和y分别表示横、纵向；vi为接触点处车轮前进速度；Δvi为接触点处车轮与钢轨的相对速度；v为列车前进速度。

蠕滑率是按接触斑坐标系定义的，而接触斑本身的位置在大地坐标系是变化的。在接触斑坐标系中，左、右轮轨的相对速度差表示为f(vWi,vri)。 其中，

(4)

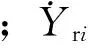
根据式(2)和式(3)，可得轮轨蠕滑率为

(5)

在实际轮轨关系中存在车轮谐波磨耗的情况下，轮轨接触是既有轮轨振动又有接触状况的一个边滚边振的状态。轮轨的材料都是弹性体，其接触产生的接触斑也可考虑为1个弹簧系统。而轮轨接触表面的不平顺可引发弹簧系统产生接触振动[8]。

由式(2)和Hertz弹性接触理论可以求得轮轨间的动态接触力Fz[8]为

(6)

其中，

式中：C为由轮轨接触斑附近的材料特性和曲率半径所决定的参数；H(δZi)为单位阶跃函数。

式(6)中，当δZi<0时即左、右侧轮轨法向压缩量均小于0，定义为轮对与钢轨之间的距离>0，左、右轮轨法向载荷为0。

轮轨接触蠕滑力的非线性关系[9]为

Fc=Fc(FN,ξc,φ,q)

(7)

式中：FN为轮轨接触法向力；φ为自旋角；q为轮轨接触参数。

式(7)中，横向蠕滑率ξy，纵向蠕滑率ξx，自旋角φ构成了对纵向蠕滑力Fx和横向蠕滑力Fy的求解非线性方程式，式中还包含了轮轨接触几何特性及轮轨接触参数q等因素。

在振动状态下轮轨接触法向力FN为与钢轨横向和垂向振动加速度有关的时变值，则

FN=Fz

(8)

由式(5)—式(8)可知，实际的轮轨接触蠕滑力是在轮轨间接触振动力(如轨道板振动、钢轨弹性变形和接触振动及车轮谐波磨耗造成轮轨瞬态接触脱离而引起的轮轨间动作用力)及瞬态轮轨接触位置等一系列因素作用下产生的。考虑车轮谐波磨耗及轮轨接触振动的蠕滑力又可表示为

Fc=Fc(Fz,ξc,φ,q)

(9)

2　数值模型的建立

采用ANSYS和UM软件建立的CRTS型无砟轨道模型由轨道板和柔性钢轨组成，其中柔性模块采用固定界面综合模态法进行处理。轨道板使用常见CRTS型双块式无砟轨道，模态截止频率为994.628 Hz。柔性钢轨处理成连续弹性离散支持的无限长Timoshenko梁，廓形采用中国标准的60轨[10]，柔性模块下的钢轨模态截止频率为1 861.17 Hz，在轨道板与柔性钢轨之间使用力元连接模拟轨枕。

采用CRH2型高速列车建立车辆仿真模型。将高速列车考虑为3个刚性模块，即轮对、车体和构架。这3个部分之间采用力元连接，其中构架与车体和车体与轮对之间采用横向止挡、抗蛇形减震器、一系二系悬挂等多个非线性特性连接力元，整个车辆动力学模型共有50个自由度。

轮轨间的接触蠕滑力采用Kalker非线性蠕滑理论进行计算，轨道施加美国6级轨道不平顺谱。车轮谐波磨耗采用在实际高速列车车轮谐波磨耗统计值中的几种典型状态进行研究[11]。根据实测统计可得，1，6和11阶谐波磨耗阶数、0.1和0.3 mm波深是最为典型的车轮谐波磨耗表现形式，也是本文进行研究的车轮谐波磨耗表现形式。仿真模型中的车速为200 km·h-1。

双块式无砟轨道振动模型拓扑图、车辆—柔性轨道耦合动力学模型分别如图2和图3所示。图中：Kpv和Cpv分别为钢轨与地面接触力元的刚度和阻尼。车辆—柔性轨道耦合动力学仿真模型拓扑图见文献[7]。

图2　双块式无砟轨道振动模型拓扑图

图3　车辆—柔性轨道耦合动力学模型

3　基于柔性轨道的高速轮轨接触蠕滑特性

3.1　轮轨接触特性

高速轮轨接触的蠕滑质量与轮轨接触的条件相关。车轮谐波磨耗引起高速轮轨的接触状态发生变化，使得轮轨因垂向力作用而发生高频率震荡，极大地恶化了轮轨接触条件，破坏蠕滑状态，加剧轮对自激振动[12]；轮对自激振动又加剧了轮对蛇形运动，影响其冲角和横移量。轮轨垂向激烈振动带来的垂向冲击通过轮轨蠕滑接触面传递至钢轨，并通过钢轨扣件传递至轨道板，引起钢轨和轨道板的振动和冲击。同时钢轨和轨道板的振动和冲击反作用于轮轨接触振动系统和轮轨接触蠕滑系统，使得整个车轮/钢轨系统产生和传递的高频振动和瞬态冲击形成自反馈体系，并对轮轨接触蠕滑特性影响极大。

车轮谐波磨耗对轮轨接触体系的激扰来自谐波磨耗车轮自身对钢轨的谐波激励。采用6种典型谐波磨耗车轮(阶数分别为1，6和11阶，波深分别为0.1和0.3 mm)与正常车轮进行高速轮轨接触对比研究。不同谐波磨耗下的钢轨垂向加速度最大值、轮轨垂向力及轮对垂向加速度的最大值和平均值见表1。相对于不考虑柔性轨道时的轮轨接触振动特性而言，当由刚性钢轨的无钢轨振动加速度等振动特性改善为随车轮谐波磨耗变化而变化的动态振动特性后，由此带来轮对振动特性的改善，即由刚性轮对对刚性钢轨的振动变化为刚性轮对对柔性钢轨的振动。由表1可知：在影响轮轨垂向力变化的因素里，谐波磨耗的波深较阶数的影响大，轮轨垂向力、钢轨垂向加速度和轮对垂向加速度的变化趋势保持一致；6和11阶时轮轨垂向力最大值的增幅很大，11阶0.3 mm波深时达到无谐波磨耗时的7.27倍，这个变化趋势也反映在钢轨垂向加速度的变化上；6阶谐波磨耗后，钢轨垂向加速度和轮对垂向加速度最大值急剧增大，轮对垂向加速度的变化趋势与钢轨垂向加速度的一样，11阶0.3 mm波深时钢轨垂向加速度最大值为无谐波磨耗时的49.6倍；轮对垂向加速度最大值在11阶0.3 mm波深时达到最大，为无谐波磨耗时的20.35倍，轮对平均垂向加速度在11阶0.3 mm波深时达到最大，为无谐波磨耗时的15.18倍;轮轨接触脱离时间比例在不同谐波磨耗阶数和波深时变化剧烈，6阶0.1 mm波深时的轮轨接触脱离时间比例为1阶0.3 mm时的4倍，并在后续车轮谐波磨耗状况时保持高速增长；在发生轮轨接触脱离时，轮轨间的空间距离大于零，轮轨动作用力为零。

表1　不同车轮谐波磨耗阶数和波深下的轮轨接触振动特性

3.2　纵向和横向蠕滑率

考虑和不考虑柔性钢轨的仿真模型变化最大的是轮轨接触脱离时间比例轮轨间蠕滑特性。它们的对比结果见表2。轮轨接触脱离时间影响其蠕滑率，纵向蠕滑率绝对平均值在出现车轮谐波磨耗现象后急剧增大到无谐波磨耗时的14倍，而纵向蠕滑率最大值和横向蠕滑率绝对平均值变化不明显，横向蠕滑率最大值随谐波磨耗的发展而明显增加[13]。

仿真计算各阶数及波深谐波磨耗轮对在车辆—柔性轨道耦合下的纵向、横向蠕滑率和轮轨接触脱离时间比例，结果见表3。不同车轮谐波磨耗阶数和波深下的纵向和横向蠕滑率时程曲线对比如图4和图5所示。

表2刚性钢轨和柔性钢轨接触条件下的轮轨接触脱离时间比例对比

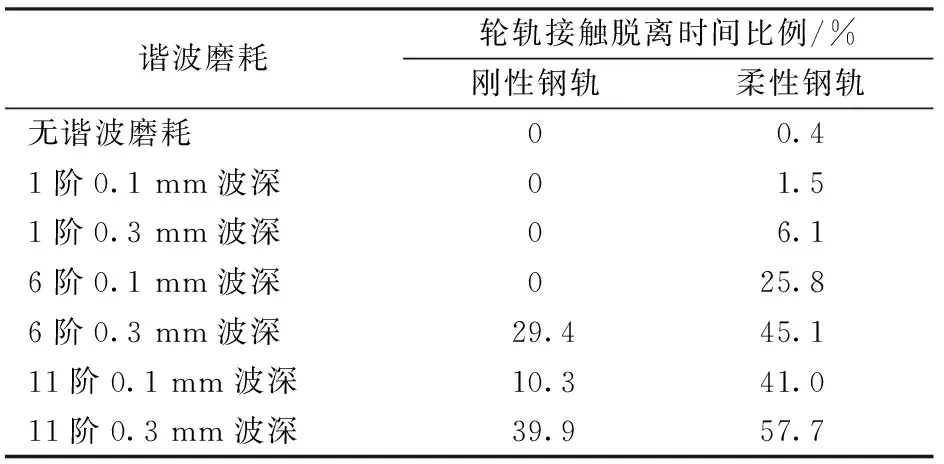
谐波磨耗轮轨接触脱离时间比例/%刚性钢轨柔性钢轨无谐波磨耗00.41阶0.1mm波深01.51阶0.3mm波深06.16阶0.1mm波深025.86阶0.3mm波深29.445.111阶0.1mm波深10.341.011阶0.3mm波深39.957.7

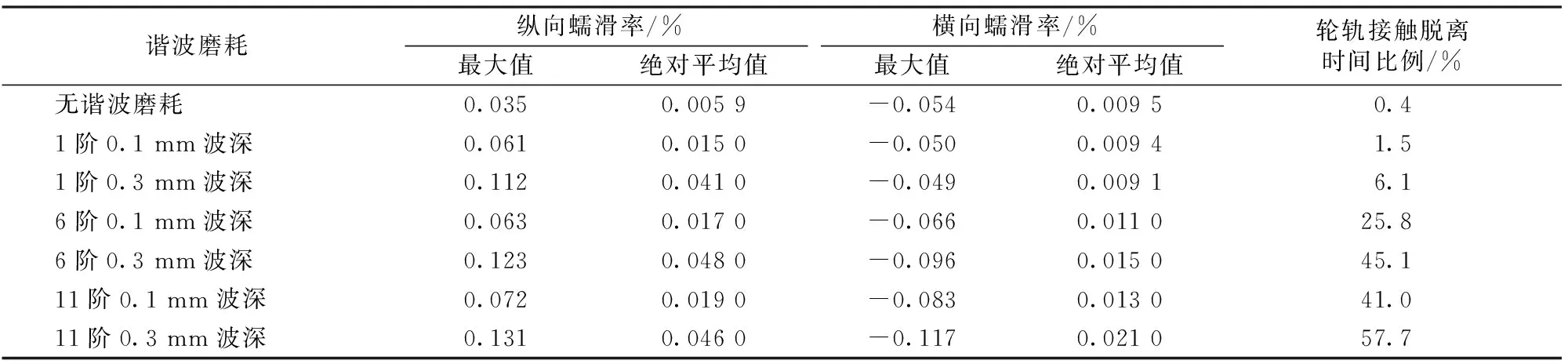
表3　不同车轮谐波磨耗阶数和波深下的轮轨接触蠕滑率和轮轨接触脱离时间比例

由表3和图4、图5可知：车轮谐波磨耗的阶数和波深都对横向蠕滑率有较大影响，波深的影响要大于阶数的，且在同样的阶数下波深越大纵向蠕滑率和横向蠕滑率的最大值也更大；纵向蠕滑率平均值和横向蠕滑率平均值的增长趋势与谐波磨耗的变化规律保持一致，且在发生谐波磨耗后纵向和横向蠕滑率急剧增大；横向蠕滑率平均值随谐波磨耗变化规律的增长要小于纵向蠕滑率平均值。

图4　不同车轮谐波磨耗阶数和波深下的纵向蠕滑率

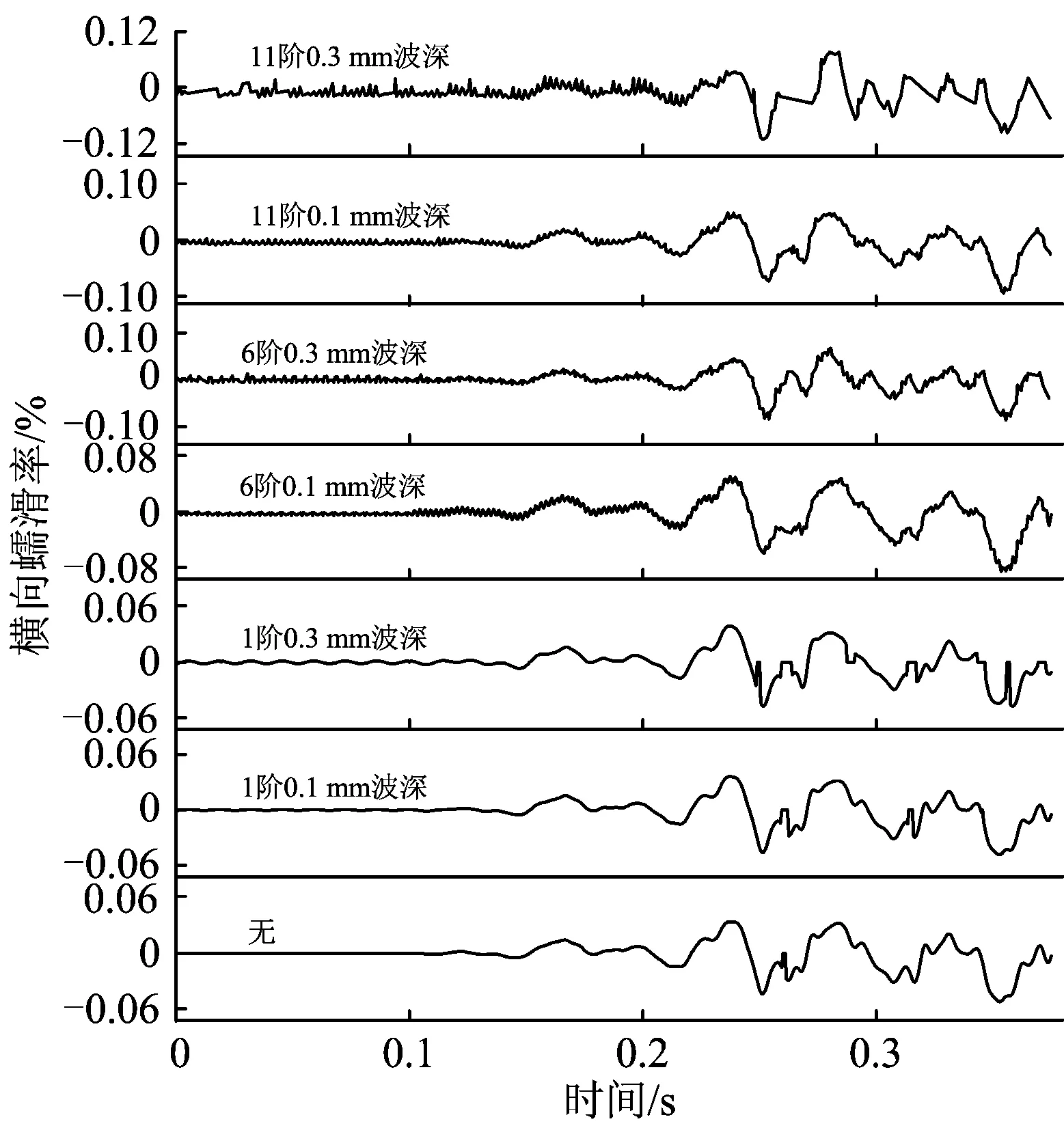
图5　不同车轮谐波磨耗阶数和波深下的横向蠕滑率

3.3　纵向和横向蠕滑力

纵向蠕滑力对列车牵引特性有重大意义，且受到许多因素影响[14]。车轮谐波磨耗导致高速轮轨接触不平稳，恶化列车行车品质并引发轮轨间垂向和横向的高频振动以及振动带来的轮轨间瞬态高速冲击，继而通过轮轨接触系统反馈至轨道板，进一步加剧钢轨振动，并造成轮轨蠕滑接触斑位置、蠕滑区和黏着区的范围变化剧烈，严重影响高速轮轨接触蠕滑特性[15]。不同车轮谐波磨耗阶数和波深下的纵向、横向蠕滑力和轮轨接触脱离时间比例见表4，它们的时程曲线分别如图6和图7所示。

由表4和图6、图7可知：车轮谐波磨耗极大地影响轮轨纵向蠕滑力，谐波磨耗的波深对纵向蠕滑力的影响大于其阶数的；纵向蠕滑力平均值在1阶0.3 mm波深时为953.954 N，为无谐波磨耗时的2.89倍[14]；谐波磨耗阶数和波深的变化极大地影响轮轨接触脱离时间比例，进而影响轮轨蠕滑力，在车轮谐波磨耗为11阶及0.3 mm波深时，横向和纵向蠕滑力均达到最大值，分别为车轮无谐波磨耗时的6.7和8.57倍。

图6　不同车轮谐波磨耗阶数和波深下的纵向蠕滑力

图7　不同车轮谐波磨耗阶数和波深下的横向蠕滑力

在不考虑柔性轨道时，轮轨间接触振动产生的作用力对钢轨的反馈弱于考虑柔性轨道时的柔性轨道会传递部分轮轨间接触振动，并对轮轨接触蠕滑产生反馈。总体来说，不考虑柔性轨道时，轮轨间滚动接触振动特性较考虑柔性轨道时更为激烈。从反映轮轨蠕滑特性的蠕滑力数值来看，不考虑柔性轨道时的纵向蠕滑力最大值和横向蠕滑力最大值均随着车轮谐波磨耗的发展而增加，纵向蠕滑力绝对平均值和横向蠕滑力绝对平均值均随谐波阶数的增加而增加，在11阶0.3 mm波深时达到最大，分别为无谐波磨耗时的1.712和2.146倍[13]。

表4　不同车轮谐波磨耗阶数和波深下的轮轨接触蠕滑力和轮轨接触脱离时间比例

4　结　论

(1)由高速列车车轮谐波磨耗引发的轮轨接触脱离现象极大影响轮轨接触振动特性，恶化轮轨接触条件，并对车轮—钢轨耦合系统产生高频瞬态冲击和振动，恶化轮轨的接触蠕滑条件。轮轨接触脱离时间比例随车轮谐波磨耗阶数和波深的增加而快速增加，在车轮谐波磨耗为11阶和0.3 mm波深时轮轨接触脱离时间比达到最大，为车轮无谐波磨耗时的147.8倍；同时钢轨垂向加速度最大值和轮对垂向加速度最大值分别为车轮无谐波磨耗时的49.6和20.35倍。

(2)随着车轮谐波磨耗阶数的增加，轮轨垂向力和轮对垂向加速度的最大值和平均值、钢轨垂向加速度的最大值等快速增加，而纵、横向蠕滑力和蠕滑率的最大值以及平均值增长缓慢。

(3)车轮谐波磨耗波深对高速轮轨接触蠕滑特性的影响大于车轮谐波磨耗阶数的影响，即同阶数不同波深的车轮谐波磨耗对轮轨蠕滑特性的影响较同波深不同阶数时的影响更为明显，而且在车轮谐波磨耗为6和11阶时波深的影响更加显著。在车轮谐波磨耗为11阶和0.3 mm波深时，轮轨垂向力最大值、钢轨垂向加速度最大值、轮对垂向加速度最大值和平均值、纵向蠕滑率平均值、纵向蠕滑力绝对平均值、横向和纵向蠕滑力的最大值分别为无谐波磨耗时的7.27，49.6，20.35，15.18，7.8，9.064，6.7和8.57倍。

[1]陈伟. 高速列车车轮多边形问题研究[D]. 成都：西南交通大学,2011.

(CHEN Wei.Research on Wheel Polygonization of High-Speed Train[D]. Chengdu：Southwest Jiaotong University,2011. in Chinese)

[2]张雪珊，肖新标，金学松. 高速车轮椭圆化问题及其对车辆横向稳定性的影响[J]. 机械工程学报，2008，44(3):50-56.

(ZHANG Xueshan,XIAO Xinbiao,JIN Xuesong.Influence of High Speed Railway Wheels Ovalization on Vehicle Lateral Stability[J].Chinese Journal of Mechanical Engineering, 2008，44(3):50-56.in Chinese)

[3]JOHANSSONA Nielsen Jco. Out-of-Round Railway Wheels-Wheel-Rail Contact Forces and Track Response Derived from Field Tests and Numerical Simulations[J]. Journal of Rail and Rapid Transit，2003，217:135-146.

[4]黄江伟. 考虑轮对柔性的轮轨动力行为研究[D]. 成都：西南交通大学，2012.

(HUANG Jiangwei.Study of Wheel/Rail Dynamic Behavior Considering Wheelset Structural Flexibility[D]. Chengdu：Southwest Jiaotong University,2012. in Chinese)

[5]王忆佳，曾京，罗仁，等. 高速列车车轮多边形化对车辆动力学性能的影响[J]. 四川大学学报：工程科学版，2013，45(3):176-182.

(WANG Yijia,ZENG Jing,LUO Ren,et al.Effect of Polygonal Wheel on Vehicle Dynamic Performance[J].Journal of Sichuan University：Engineering Science Edition，2013，45(3):176-182.in Chinese)

[6]宋颖. 高速车轮失圆对轮轨动力作用的影响及其监测方法研究[D]. 北京：北京交通大学，2010.

(SONG Ying.Study on Influence of Out-of-Round High-Speed Railway Wheels on Wheel/Rail Interaction Force and Monitoring Method[D].Beijing：Beijing Jiaotong University,2010. in Chinese)

[7]翟婉明. 车辆—轨道耦合动力学[M]. 3版.北京：科学出版社. 2007.

(ZHAI Wanming.Vehicle-Track Coupling Dynamics [M].3rd ed.Beijing:Science Press,2007.in Chinese)

[8]刘韦，马卫华，罗世辉，等. 考虑轮对弹性的车轮振动及车轮多边形化对轮轨力影响研究[J]. 铁道学报，2013，35(6):28-34.

(LIU Wei,MA Weihua,LUO Shihui,et al.Reasearch on Influence of Wheel Vibration and Wheel Polygonization on Wheel-Rail Force in Consideration of Wheelset Elasticity[J].Journal of the China Railway Society, 2013，35(6):28-34.in Chinese)

[9]DMITRY Pogorelov.Universal Mechanism User’s Manual [M].Bryansk:Bryansk State Techniacl University，2011.

[10]翟婉明，夏禾. 列车—轨道—桥梁动力相互作用理论与工程应用[M]. 北京：科学出版社，2011.

(ZHAI Wanming,XIA He. Train-Track-Bridge Dynamic Interaction:Theory and Engineering Application [M].Beijing:Science Press,2011.in Chinese)

[11]黄照伟. 车轮磨耗及其对车辆动力学性能的影响[D].成都：西南交通大学，2012.

(HUANG Zhaowei.Wheel Tread Wear and Its Influence on Dynamic Performance of Vehicles[D]. Chengdu：Southwest Jiaotong University,2012. in Chinese)

[12]肖乾，穆明，周新建，等. 高速列车轮轨材料滑动摩擦实验研究[J]. 华东交通大学学报， 2013，30(5):24-29.

(XIAO Qian,MU Ming,ZHOU Xinjian,et al.Study on Sliding Friction Coefficient of High-Speed Wheel-Rail Materials[J].Journal of East China Jiaotong University, 2013，30(5):24-29.in Chinese)

[13]肖乾，程树，张海，等.车轮谐波磨耗对直线线路上高速轮轨接触蠕滑特性的影响[J].中国铁道科学，2016,37(6)：60-68.

(XIAO Qian,CHENG Shu, ZHANG Hai,et al. Influence of Wheel Harmonic Wear on Creep Characteristics of High Speed Wheel-Rail Contact on Straight Line[J].China Railway Science,2016,37(6)：60-68.in Chinese)

[14]肖乾，徐红霞，成棣，等.不同轮轨冲角下高速轮轨稳态滚动接触的蠕滑特性[J].中国铁道科学，2014,35(1)：60-66.

(XIAO Qian,XU Hongxia, CHENG Di,et al. Creep Characteristics of High-Speed Wheel-Rail Steady-State Rolling Contact under Different Attack Angles[J].China Railway Science,2014,35(1):60-66.in Chinese)

[15]程树. 高速列车谐波磨耗车轮/钢轨滚动接触瞬态动力学分析[D].南昌：华东交通大学，2016.

(CHENG Shu.Transient Dynamics Analysis of High Speed Train Rolling Contact of Harmonic Wear Wheel/Rail[D].Nanchang:East China Jiaotong University, 2016. in Chinese)