海床土刚度非线性的钢悬链式立管响应分析

周阳， 杨超凡， 黄维平

(1.国家海洋局第二海洋研究所 工程海洋学重点实验室, 浙江 杭州 310012；2.上海外高桥造船有限公司, 上海 200000；3.中国海洋大学 山东省海洋工程重点实验室, 山东 青岛 266100)

海床土刚度非线性的钢悬链式立管响应分析

周阳， 杨超凡， 黄维平

(1.国家海洋局第二海洋研究所 工程海洋学重点实验室, 浙江 杭州 310012；2.上海外高桥造船有限公司, 上海 200000；3.中国海洋大学 山东省海洋工程重点实验室, 山东 青岛 266100)

基于大挠度柔性梁理论和弹性基础梁理论，本文建立了钢悬链式立管与海床土非线性相互作用的数学模型。用大挠度柔性梁来模拟立管的悬垂段，用弹性基础梁来模拟立管的触地段。其中触地段海床土的刚度根据管线与海床土相互作用的载荷位移曲线P-y来确定，更真实地模拟海床基础。研究表明：基于该模型开发的程序能与商用软件OrcaFlex较好地吻合，由于所开发程序可以采用较大的计算单元，其计算时间大大减少。与线性海床模型相比，通过该模型计算得到的立管触地点附近的疲劳损伤增幅1～3倍，有利于安全的设计。

钢悬链式立管；柔性梁；管土相互作用；非线性海床；疲劳破坏；大挠度

随着海洋油气开采逐步走向深海，为适应更加严峻的海洋条件，不同类型的海洋工程结构应运而生。钢悬链式立管(steel catenary riser，SCR)是20世纪90年代初期发展起来的一种新型深水立管系统，具有成本低和可承受高温高压等优点，是浮式平台输入输出的首选立管系统。钢悬链式立管集海底管线与立管于一身，一端连接井口，一端连接浮式结构[1]，迄今为止，已有大量SCR安装在西非、墨西哥湾及巴西等海域。

钢悬链式立管由悬垂段和海底流线段组成，悬垂段和海底流线段是由钢管焊接而成的一条整体管线，悬垂段和海底流线段的分界点是触地点。当钢悬链式立管的悬垂段随浮式平台运动而发生运动时，或者在波浪等外荷载的作用下，海底流线段也随之产生运动，从而导致了钢悬链式立管与海床的相互作用[2-3]。研究表明，钢悬链式立管与海床相互作用对立管的动力响应和疲劳寿命有较大的影响[4-6]。然而，由于立管与海床相互作用的非线性及其对疲劳性能影响的不确定性，目前工程业普遍采用设计规范推荐的过度简化的方法来研究立管与海床土的相互作用[7]，即采用线性刚度海床土来模拟管土相互作用。Brigde等对钢悬链式立管的研究结果表明疲劳寿命的评估与选用的海床土的刚度有关[8]。因此为了能够准确的评估立管触地点处的疲劳寿命，需要采用合理的海床模型。

根据相关的试验结果及数值分析结果，Aubeny提出了模拟立管与海床相互作用的非线性P-y曲线，其中P为土抗力，y为立管的贯入深度[9]。Nakhaee基于Aubeny提出的立管与海床土非线性相互作用模型对CABLE 3D程序进行了改编[10-11]，以更真实地模拟海床土的刚度。在其研究中，立管被认为是经历周期性振动，即立管与海床土是完全的接触、分离及再接触。本文基于Aubeny提出的P-y曲线进行数学编程建模，程序考虑了钢悬链式立管与海床相互作用时可能位于弹性回弹、部分分离或完全分离的情况，是一个完整的钢悬链式立管与海床土非线性相互作用的力学模型。另外，对不同海床土壤刚度的计算结果进行了比较。

1 立管与海床相互作用模型

1.1 模型描述

图1为Aubeny提出的P-y曲线，立管与海床相互作用的P-y曲线可以分为两个阶段：1)沿着路径0-1-1′的骨干曲线，即立管初次贯入土壤时遵循的路径；2)大变形的回弹路径1-2-3-1，包括管土完全接触即弹性回弹路径1-2，管土的部分分离，即路径2-3以及沿着路径3-1的再接触与再加载。在这个过程中，立管向上运动时的管土完全分离并不会在每一种工况及触地点区域所有的点发生。在沿着滞回圈任何一点都可能发生反向的位移，如图1中虚线所示。同时，周期荷载也可能完全在滞回圈内。其中从2点到P=0处的点以及部分分离阶段2-3，立管均受到吸力作用。Aubeny分别提出了骨干曲线，弹性回弹、部分分离及再接触阶段的经验公式[9,12]。

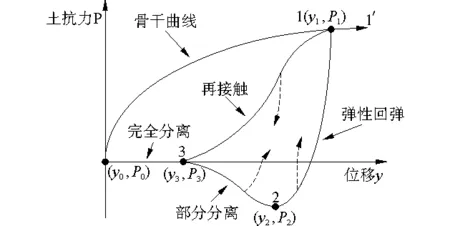
图1 典型p-y曲线Fig.1 Typical p-y behavior

1.2 程序编译

本文用于计算锚泊或立管系统与浮式平台相互作用的非线性有限元分析程序基于大挠度柔性梁理论。柔性梁理论由Garrett首先提出，适用于不可伸长的杆[13];而后Paulling等[14-15]将其扩展为适用于小伸长的杆;Chen将其进一步拓展为适用于大伸长的锚泊线[16]。

根据Chen的论文，小伸长柔性杆的运动方程和约束条件分别为

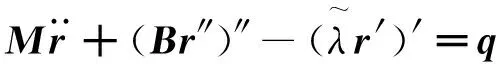
(1)

(2)

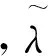
垂向海床土的支撑力可以表示为

Pt=Pti+ktiδy

(3)

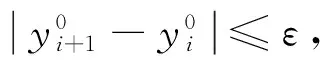
在动态分析时，这个过程会更加复杂。具体分成以下几步：

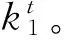
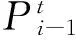
2 模型计算结果及分析

2.1 模型验证

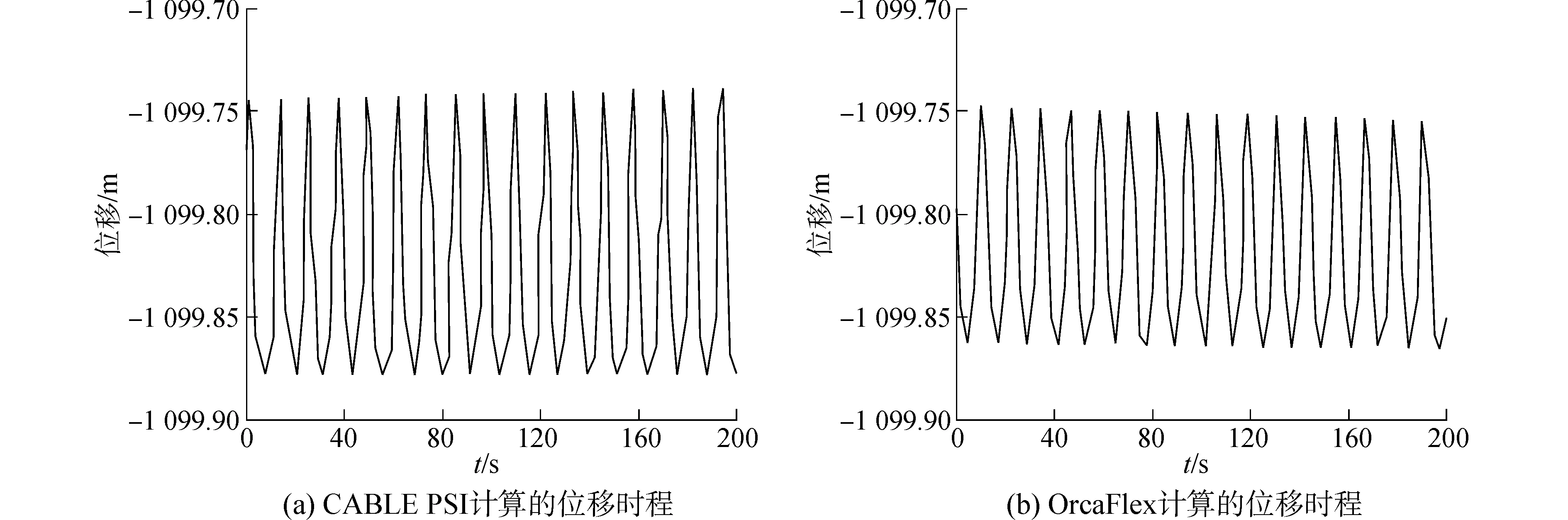
图3 立管位移时程对比图Fig.3 Time history of displacement of SCR

为了验证所提出模型的正确性，采用上述模型编制了钢悬链式立管与海床土相互作用的分析程序CABLE PSI，该程序充分考虑了立管与海床土的非线性相互作用，考虑了海床土壤特征对于立管法向约束力的影响。将模型计算结果同现有商用软件OrcaFlex的计算结果进行比对。本文数值模拟选取的是一根典型的钢悬链式立管[17-18]，立管的上端连接在船体上，在动态模拟过程中仅考虑船体的垂荡运动，垂荡幅值为2 m，垂荡周期为12 s。该立管长2 400 m, 外径0.355 6 m，内径0.304 8 m，密度7 850 kg/m3, 弹性模量2.07×108kPa，模拟水深1 100 m，顶张力2 100 kN，悬挂角16°。数值模型的计算参数如下：时间步长为0.02 s，计算总时长为3 700 s，单元长度为6 m。

海床土的剪切强度是随着深度线性增加的，即满足

S=S0+Sgy

(4)

式中：S在深度y处的土壤剪切强度，S0是在海床处的土壤剪切强度，Sg是剪切强度梯度。本文中，S0为1.8 kPa，Sg为 1.0 kPa/m。

分别用CABLE PSI和OrcaFlex对立管进行静态分析。图2给出了他们的静态位置对比情况，x、y分别为立管节点的横坐标与纵坐标，通过比较发现，两者基本上呈现相同的静态位形，由于OrcaFlex中钢悬链式立管是通过没有质量的弹簧连接的质量块简化模拟的，而在CABLE PSI中钢悬链式立管是通过大挠度柔性梁模拟的，所以两者之间存在一定差异是合理的。

图2 立管静态位形对比图Fig.2 Static configuration of SCR

在静态分析结束后，分别用CABLE PSI和OrcaFlex对立管进行动态分析，由于两者所采用的管土相互作用模型不同，且OrcaFlex并不能考虑土壤的吸力作用，因此两者计算结果会有一定差异。图3给出了两者立管动态分析中触地点区域的垂向位移时程图，通过比较发现，两者程序都趋于稳定之后，触地点区域的动态位移幅值虽然并不完全相同，但均为0.06 m左右。图4给出了相应的频谱分析，从频谱图比较可以看出，图4(a)和图4(b)均有两个主要频率，且都在0.08 Hz和0.16 Hz附近。由此可见CABLE PSI程序的计算结果与商用软件OrcaFlex的计算结果能较好吻合。

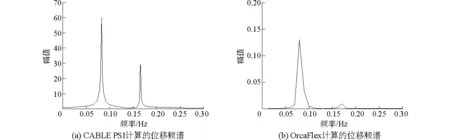
图4 立管位移频谱对比图Fig.4 Spectrum of displacement of SCR

2.2 载荷位移曲线

本文CABLE PSI程序所建立的数值模型采用载荷位移曲线，即P-y曲线来模拟立管与海床土的相互作用，将海床的土壤刚度看作是非线性的，而不是一个定值，那么利用该程序计算得到的海床土法向约束力与立管位移之间的关系曲线也应该与该模型的P-y曲线符合。

图5 CABLE PSI计算得到的的P-y曲线Fig.5 P-y curves calculated by CABLE PSI

图5给出了触地点区域某一节点的法向约束力与该节点位移之间的关系曲线，即实线部分，而虚线为利用骨干曲线经验公式绘制出的骨干曲线。土抗力大于0，表明此时立管受到土壤的支撑力作用；土抗力小于0，表明此刻立管发生上举运动，受到土壤的吸力作用，并且该节点处SCR与土壤接触后，发生完全分离，再与土壤再次接触。因此，由图5可知，该节点的荷载位移曲线遵循采用的P-y曲线。从而验证了该程序在管土相互作用的过程中确实是采用P-y曲线控制海床土法向约束力与SCR位移之间的关系，即该程序模型能够对立管与海床土的非线性相互作用进行分析。

2.3 海床土非线性刚度与线性刚度对比

线性刚度的海床其刚度只与SCR的单位长度湿重和直径有关，而非线性刚度的海床其刚度与真实的海床土地基有关，通过P-y曲线的形式表现出来。本节对海床土非线性刚度与线性刚度的计算结果进行了比较，其中非线性刚度海床土壤强度分为低强度、中强度和高强度三种情况，具体参数见表1，其他计算参数与2.1节相同。

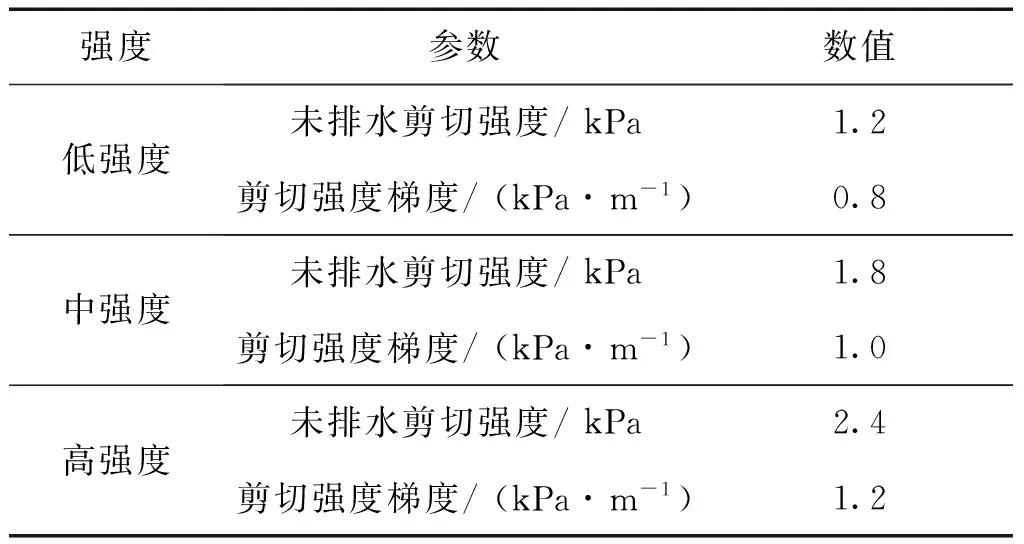
表1 土壤参数

图6给出了线性刚度海床土、低强度海床土、中强度海床土和高强度海床土在SCR最大贯入深度时对应的触地点区域的立管位形图。可以看出海床土刚度的不同对SCR的位形有着较显著的影响。在垂荡幅值皆为2 m的情况下,低强度海床土的立管最大贯入深度为0.113 m，中强度海床土的为0.058 m，高强度海床土的为0.038 m，线性刚度海床土的为0.189 m，可见低强度海床土是分析的三种非线性土壤中最大贯入深度与线性海床土结果最为相近的。因此通过线性海床土模型计算得到的结果其所能表征的是土壤刚度较低的海床，而非线性海床土模型能考虑不同海床土壤刚度对钢悬链式立管的影响。

图6 立管动态位形对比图Fig.6 Dynamic configuration of SCR

图7给出了分析时间为500～800 s的这300 s的时间历程中不同土壤刚度情况下，最大贯入深度节点处SCR垂向位移响应时程图和频谱图。从图中可以看出不同土壤刚度情况下，SCR该节点的垂向位移响应均呈现出明显的周期性，且幅值变化不大：

1)线性刚度海床土情况下最大贯入深度节点处SCR垂向位移响应稳定在[-1 100.19,-1 100.145](以海平面为位移零点)，幅值约为0.045 m；

2)低强度海床土情况下该节点的垂向位移响应稳定在[-1 100.12,-1 099.97]，幅值约为0.05 m；

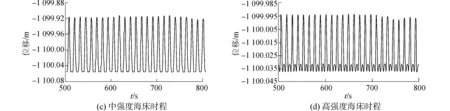
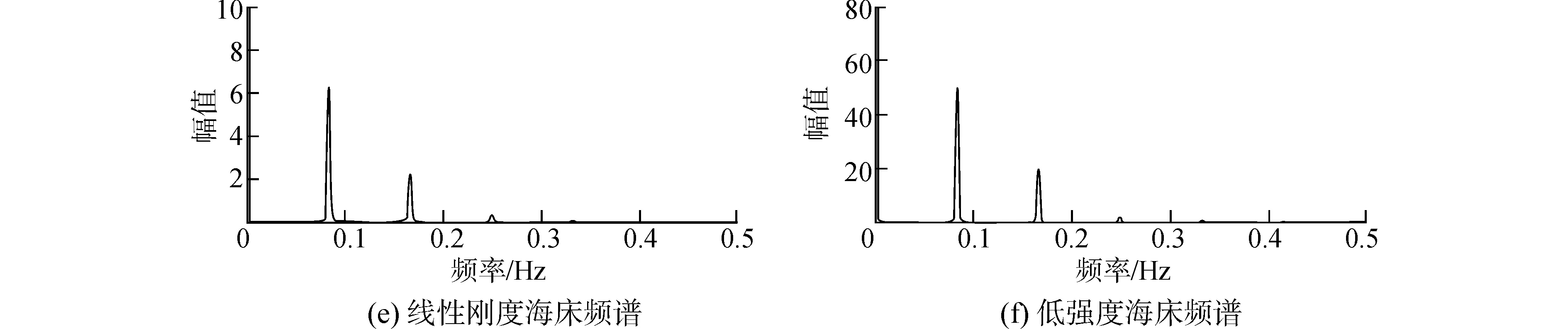
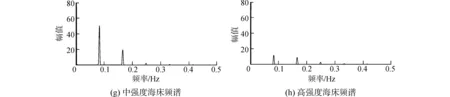
图7 不同土壤刚度情况下位移响应时程及频谱图Fig.7 Time history and spectrum of displacement under different soil properties

3)中强度海床土情况下该节点的垂向位移响应稳定在[-1 100.05,-1 099.92]，幅值约为0.07 m；

4)高强度海床土情况下该节点的垂向位移响应稳定在[-1 100.04,-1 099.99]，幅值约为0.05 m。

可以看出不同土壤刚度情况下，SCR的垂向运动响应还是有一定差异的。

从图7的频谱分析中可以看出不同土壤刚度情况下，SCR的振动频率成分皆为0.083 Hz和0.166 Hz，其中前者恰为立管上部的垂向运动频率，可见SCR的振动频率主要是受到外荷载的振动频率的影响，与海床土的性质关系不大。

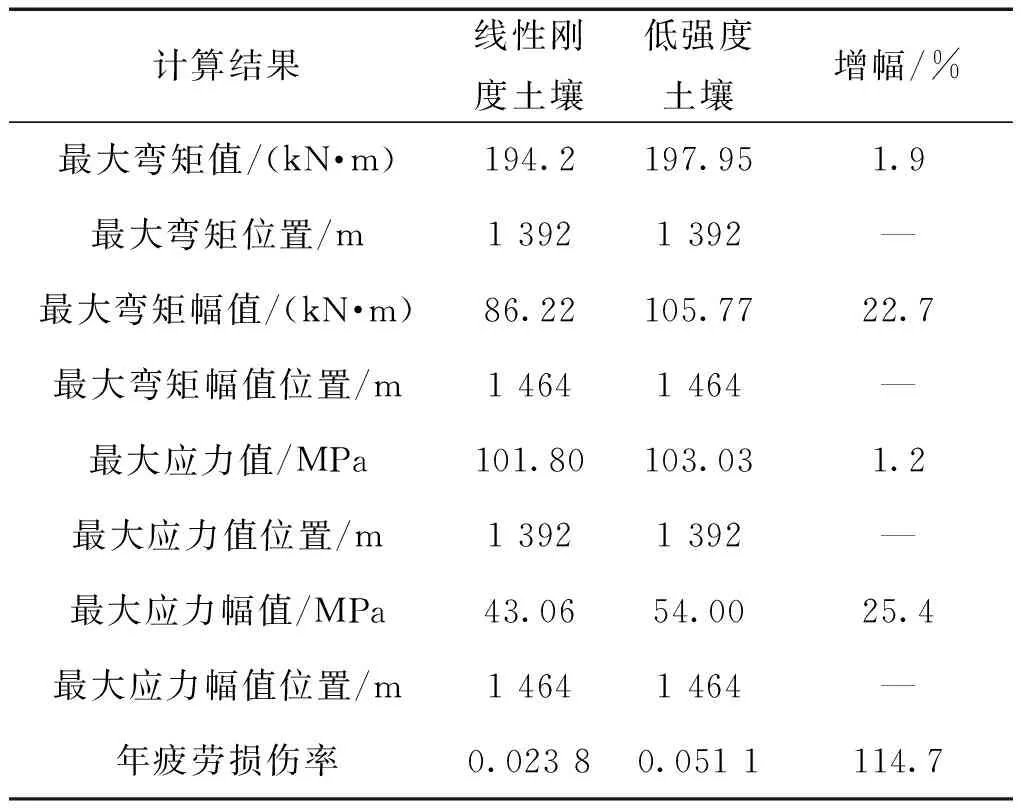
表2 土壤刚度对立管动态响应的影响

表2给出了线性刚度海床土与低强度海床土这两种情况下，钢悬链式立管的最大弯矩值、最大弯矩幅值及其位置，最大应力值、最大应力幅值及其位置和对应的最大年疲劳损伤率，其中位置是指从SCR上端开始沿立管轴向的距离。通过比较可知，两者的最大弯矩幅值和最大应力幅值差异非常显著，线性刚度土壤情况下，最大弯矩幅值为86.22 kN·m，而低强度土壤情况下，最大弯矩幅值为105.77 kN·m，后者增幅22.7%。线性刚度土壤情况下，最大应力幅值为43.06 MPa，而低强度土壤情况下，最大应力幅值为54.00 MPa，后者增幅25.4%。可见海床土刚度对于触地点区域弯矩幅值及应力幅值有较大影响。年疲劳损伤率的计算结果也验证了海床土刚度对于触地点区域的疲劳寿命影响较大。线性刚度土壤情况下年疲劳损伤率为0.023 8，而低强度土壤情况下年疲劳损伤率为0.051 1，后者增幅114.7%。另外，计算得到中强度土壤情况下立管的年疲劳损伤率为0.059 8，高强度土壤情况下为0.099 8。

3 结论

本文采用大挠度柔性梁模型模拟钢悬链式立管的运动，同时采用弹性基础梁模型模拟海床，而管土相互作用过程采用荷载位移曲线P-y进行模拟，建立了钢悬链式立管与非线性刚度海床的相互作用模型，具有一定先进性，开发了钢悬链式立管分析软件CABLE PSI。基于本文的研究，可以得出以下结论：

1)通过与商用软件初步比较，CABLE PSI程序的计算结果与商用软件OrcaFlex的计算结果能较好吻合，验证了所建立模型的正确性。

2)线性土壤与非线性土壤相比，线性土壤刚度SCR的贯入深度较大，触地点区域的SCR垂向位移幅值有一定差异。但是在上部结构的周期运动情况下，SCR的振动频率主要受外界荷载的周期影响，与海床土的性质关系不大。

3)海床土壤的刚度变化对立管的运动响应、弯矩以及疲劳寿命有着显著影响，非线性土壤的立管疲劳损伤率是线性土壤的2～4倍多，这说明采用线性刚度土壤模拟管土相互作用与实际情况有一定差距。

钢悬链式立管与海床土之间的相互作用是一个比较复杂的过程，除了海床土的刚度非线性问题，还与上部结构的运动特征、海床土的物理力学性能、顶张力以及立管本身的结构形式等多种因素有关，因此，其模拟和计算方法有待深入研究。

[1]黄维平, 李华军. 深水开发的新型立管系统——钢悬链线立管(SCR)[J]. 中国海洋大学学报, 2006, 36(5): 775-780, 686. HUANG Weiping, LI Huajun. A new type of deepwater riser in offshore oil & gas production: the steel catenary riser, SCR[J]. Periodical of ocean university of China, 2006, 36(5): 775-780, 686.

[2]黄维平, 孟庆飞, 白兴兰. 钢悬链式立管与海床相互作用模拟方法研究[J]. 工程力学, 2013, 30(2): 14-18. HUANG Weiping, MENG Qingfei, BAI Xinglan. The simulation of the interaction between SCR and seabed[J]. Engineering mechanics, 2013, 30(2): 14-18.

[3]刘娟, 黄维平. 钢悬链式立管涡激振动流固耦合非线性分析方法研究[J]. 振动与冲击, 2014, 33(3): 41-45. LIU Juan, HUANG Weiping. Fluid-structure interaction analysis for VIV of Steel catenary risers[J]. Journal of vibration and shock, 2014, 33(3): 41-45.

[4]王坤鹏, 薛鸿祥, 唐文勇. 基于海床吸力和刚度衰减模型的深海钢悬链线立管动力响应分析[J]. 上海交通大学学报, 2011, 45(4): 585-589, 596. WANG Kunpeng, XUE Hongxiang, TANG Wenyong. Dynamic response analysis of deepwater steel catenary riser based on the seabed-suction and stiffness-degradation model[J]. Journal of Shanghai Jiaotong university, 2011, 45(4): 585-589, 596.

[5]王坤鹏, 薛鸿祥, 唐文勇. 基于全耦合模型和管土作用模型的深海悬链线立管触地区域疲劳特性分析[J]. 上海交通大学学报, 2014, 48(4): 576-582. WANG Kunpeng, XUE Hongxiang, TANG Wenyong. Fatigue characteristics analysis of steel catenary riser near touchdown zone based on full coupled model and SCR-soil interaction model[J]. Journal of Shanghai Jiaotong university, 2014, 48(4): 576-582.

[6]WANG Kunpeng, XUE Hongxiang, TANG Wenyong, et al. Fatigue analysis of steel catenary riser at the touch-down point based on linear hysteretic riser-soil interaction model[J]. Ocean engineering, 2013, 68: 102-111.

[7]SHIRI H. Response of steel catenary risers on hysteretic non-linear seabed[J]. Applied ocean research, 2014, 44: 20-28.

[8]BRIDGE C, LAVER K, CLUKEY E, et al. Steel catenary riser touchdown point vertical interaction models[C]//Proceedings of 2014 Offshore Technology Conference. Houston, Texas, USA: Offshore Technology Conference, 2014: 16628-MS.

[9]AUBENY C P, BISCONTIN G, ZHANG J. Seafloor interaction with steel catenary risers (Finial Project Report)[R]. Texas: Texas A&M University, 2006.

[10]NAKHAEE A, ZHANG J. Dynamic interaction between SCR and the seabed[C]// Proceedings of ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering. San Diego, CA, USA: ASME, 2007.

[11]NAKHAEE A. Study of the fatigue life of steel catenary risers in interaction with the seabed[D]. Texas: Texas A&M University, 2010.

[12]JIAO Yaguang. Non-linear load-deflection models for seafloor interaction with steel catenary risers[D]. Texas: Texas A&M University, 2007.

[13]GARRETT D L. Dynamic analysis of slender rods[J]. Journal of energy resources technology, 1982, 104(4): 302-306.

[14]PAULLING J R, WEBSTER W C. A consistent, large-amplitude analysis of the coupled response of a TLP and tendon system[C]//Proceedings of the Fifth International Symposium on Offshore Mechanics and Arctic Engineering. Tokyo, Japan, 1986, 3: 126-133.

[15]MA W, WEBSTER W C. Analytical approach to cable dynamics: theory and user manual[R]. Berkeley, CA: University of California, 1994.

[16]CHEN Xiaohong. Studies on dynamic interaction between deep-water floating structures and their mooring/tendon systems[D]. Texas: Texas A&M University, 2002.

[17]刘娟. 考虑刚体摆动的钢悬链式立管出平面运动分析方法研究[D]. 青岛: 中国海洋大学, 2013: 58-60. LIU Juan. Study of out-of-plane motion of SCRs with rigid swing[D]. Qingdao: Ocean University of China, 2013: 58-60.

[18]杨超凡. 钢悬链式立管与海床土非线性相互作用研究[D]. 青岛: 中国海洋大学, 2014: 35-40. YANG Chaofan. Study on nonlinear interaction between SCR and seabed[D]. Qingdao: Ocean University of China, 2014: 35-40.

Dynamic response analysis of steel catenary riser based on nonlinear stiffness of seabed

ZHOU Yang1, YANG Chaofan2, HUANG Weiping3

(1. Key Laboratory of Engineering Oceanography, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China; 2. Shanghai Waigaoqiao Shipbuilding CO., LTD., Shanghai 200000, China; 3. Shandong Provincial Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao 266100, China)

In this study, we establish a mathematical model of the nonlinear interaction between the steel catenary riser (SCR) and the seabed, based on the large deflection elastic beam theory and the elastic foundation beam theory. We modeled the overhang segment of a steel catenary riser as a flexible beam with large deflection and simulated the touchdown segment of the riser as an elastic foundation beam. In addition, in our simulation of the SCR-seabed interaction, we determined the stiffness characteristics of the seabed by the load-displacement (P-y) curve. The results computed by the model are consistent with those computed by the commercial software OrcaFlex. Since large elements can be used in the proposed model, the computing time is greatly reduced. In comparison with linear seabed model results, the fatigue damage at the touchdown segment of the riser computed by our nonlinear seabed model can be increased 1-3 times, which is beneficial to the security design.

SCR; flexible beam; interaction between riser and seabed; nonlinear seabed; fatigue damage; large deflection

2016-03-24.

日期：2017-01-11.

国家自然科学基金项目(51079136，51179179).

周阳(1987-), 男, 工程师, 博士； 黄维平(1954-), 男, 教授, 博士生导师.

周阳, E-mail:edit502@126.com.

10.11990/jheu.201603082

P751

A

1006-7043(2017)03-0356-07

周阳， 杨超凡， 黄维平. 海床土刚度非线性的钢悬链式立管响应分析[J]. 哈尔滨工程大学学报, 2017, 38(3):356-362.

ZHOU Yang, YANG Chaofan, HUANG Weiping. Dynamic response analysis of steel catenary riser based on nonlinear stiffness of seabed[J]. Journal of Harbin Engineering University, 2017, 38(3):356-362.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170111.1509.020.html