多体、多程问题的解题方略探析

郑行军

中学物理模型中，由多个物体组成的系统研究一直是一个难点。由于涉及对象的合理选择及复杂过程的动态分析，因此在高考试题中常以中档偏难的题目出现。下面就动量守恒定律框架下涉及的多体、多程问题的命题与解题策略进行归类说明，以期能对高三同学的复习起到一点借鉴作用。

1. 模型定义：对于研究对象为多个物体组成的系统或涉及多个过程的动量守恒问题统称为多体问题。

2. 温馨提示：多个物体相互作用经历多个运动阶段时，物理过程往往比较复杂，分析时要注意以下几点：①正确分析作用过程中各物体状态的变化情况，建立运动模型；②分清作用过程中的不同阶段，并找出联系各阶段的状态量；③合理选取研究对象，既要符合动量守恒的条件，又要方便解题。

3. 方法归类分析：

①分过程法：若系统中的物体在作用的全过程中系统动量不守恒或速度大小与过程相关联，则列式时往往要根据作用过程中的不同阶段，建立多个动量守恒方程，或将系统内的物体按作用的关系分成几个小系统，分别建立动量守恒方程联立求解。

②全过程法：若在作用全过程中系统始终符合动量守恒的条件，则在运用动量守恒定律时只须关注初、末状态的动量，而不用注重中间状态的具体细节，这样可以给解题带来很大便利。

4. 命题设计及解题策略：

命题设计1 速度关联类问题

题型分析：在研究多体、多程问题时，命题条件常常会关联物体运动的速度，这类问题的关键在于注意条件中有关参考系的关联确定：若作用過程中研究对象的速度始终相对于地面而变化，可考虑全过程法；若物体的速度与系统中其它物体相关联（如以其它物体为参考系运动），则要利用分过程法联立方程分析求解。

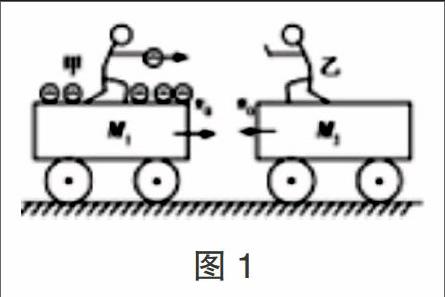
【例1】甲、乙两小孩各乘一辆小车在光滑水平面上匀速相向行驶，速率均为9m/s，甲车上有质量m0=1kg的小球若干个，甲和他的车及所带小球总质量为m1=50kg，乙车和他的车总质量为m2=40kg，甲不断地将小球以21m/s的对地水平速度抛向乙，并被乙接住，问甲至少要抛出多少个小球才能保证两车不相撞。（不考虑空气阻力）

解析：当甲、乙两车最终速度相等时，两车刚好不相撞，设此速度为v，取甲运动方向为正方向，甲、乙车及球组成的系统水平方向动量守恒，有：m1v1-m2v2=（m1+m2）v，又v1=v2=9m/s，将质量代入解得v=1m/s，方向与甲原运动方向相同。

甲每次抛出小球时，小球相对于地面的速度始终不变，可利用全过程法分析，设抛出n个球后使得甲的速度为v，对甲和被抛出的球，抛球过程水平方向动量守恒，有m1v1= nm0v0 +（m1-nm0）v，其中v0=21m/s，将质量代入得n=20个，即甲至少抛出20个球才能避免两车相撞。

点评：在研究多个物体组成的系统中，合理的选择研究对象是解题的关键，本题保证两不相撞的临界条件是末状态两车应有共同的速度，先取两车与球组成的系统，全过程动量守恒，利用全过程法即可求最终的临界速度；甲在抛球过程中由于抛出小球的速度相对地面始终不变，与甲、乙两车无关，故可以甲车和抛出的小球为系统，利用全过程法求解。

命题设计2 作用关联类问题

题型分析：在动量守恒定律的应用中，首先要注意选择的系统否满足守恒条件，在多体系统组成多过程运动中，若系统在全过程始终满足守恒条件（不受外力或所受的合外力为零），可用全过程法；若选择全过程无法满足守恒条件，则需按作用关系分解为多个小过程，分别建立动量守恒方程联立求解。

【例2】如图2所示，人与冰车质量为M，球质量为m，开始均静止于光滑冰面上，现人将球以对地速度v水平向右推出，球与档板P碰撞后等速率弹回，人接住球后又将球以同样的速度v向右推出……如此反复，已知M=16m，试问人推球几次后将接不到球？

解析：当球与档板碰撞瞬间，档板会对球产生作用力，故人在推接球的全过程中，系统动量不守恒，可考虑分过程法。

点评：在分析多体问题时，清楚物体运动的过程，灵活选用分过程法和全过程法，应用动量守恒定律可正确解题。推球过程系统动量守恒，由动量守恒定律可以求出小车的速度，球与档板碰撞瞬间动量不守恒，应用分过程法多次联立推球过程的动量守恒公式即可求出碰撞的次数。

命题设计3 多体临界问题

题型分析：在动量守恒定律的应用中，常常会遇到相互作用的两物体恰好分离、恰好不相碰，两物体相距最近，某物体恰好开始反向等临界问题，分析时应注意：①分析物体的受力、运动情况，合理的选择研究对象，判断是否满足动量守恒的条件；②分析临界状态出现所需的条件，即临界条件，条件往往表现为某个（或某些） 物理量的特定取值（或特定关系），通常表现为两物体的相对速度关系或相对位移关系，这些特定关系是求解这类问题的关键；③列方程时要注意位移或速度的同时性和相对性。

【例3】如图3所示，甲、乙两小孩各乘一辆冰车在水平冰面上游戏，甲和他的冰车的总质量M =40kg，乙和他的冰车的总质量也是40 kg。游戏时，甲推着一个质量m=20kg的箱子，让箱子和他一起以v1=2 m/s的速度滑行，乙以v2=1.75m/s的速度迎面向甲滑来。为了避免相撞，甲突然将箱子沿冰面推向乙，箱子滑到乙处时，乙迅速把箱子接住。若不计冰面的摩擦，为避免与乙相撞，问：（1）甲至少要以多大的速度（相对地面）将箱子推出？（2）甲将箱子推出的过程中至少做了多少功？

解析：（1）在推出和抓住的过程中，小孩、冰车和箱子的总动量守恒.要想刚能避免相碰，要求抓住后甲和乙的速度正好相等.此就可求得推出时的最小速度。

设箱子推出后其速度为v，甲孩的速度为v1′，以甲的初速度方向为正方向，根据动量守恒可得：mv+Mv1′=（m+M）v1；设乙孩抓住箱子后其速度为v2′，以向右为正方向，根据动量守恒可得：（m+M）v2′=mv-Mv2，刚好不相碰的条件要求：v1′=v2′，解得：v=5m/s，v1′=v2′=0.5m/s；

（2）设以最小速度推出时甲对箱子做功为W，对箱子，由动能定理得： 代入数值可得：W=135J；

点评：本题运动过程复杂，有一定的难度；分析清楚物体运动过程、找出避免碰撞的临界条件是正确解题的关键.甲将箱子沿冰面推给乙过程，甲乙的总动量守恒，乙把箱子抓住过程，乙与箱子总动量守恒，当甲与乙恰好不相撞时，甲将箱子推给乙后速度与乙接住箱子后的速度恰好相等.根据动量守恒定律和速度相等条件求解甲推箱子的速度大小的最小值；对箱子，应用动能定理可以求出功.

拓展训练：

1. 如图4所示是冲击摆装置。塑料制成的摆块用绳悬挂起来，使它只能摆动不能转动。摆块中间正对枪口处有一水平方向的锥形孔，孔的内壁垫以泡沫塑料.当弹丸射入后迅速停住，然后与摆块一起摆动，读出摆线偏离竖直方向的最大角度，就可求出弹丸的速度。某次实验中，弹簧枪射出的弹丸以某一速度v0（未知）水平射入静止的摆块，读出摆线偏离竖直方向的最大角度α=37°；然后将摆块拉到摆线偏离竖直方向的角度β=60°由静止释放，当摆块摆到最低位置时，让弹丸以相同速度v0射入，摆块恰好静止已知摆线的长度L=1.00m，不考虑空气阻力，求弹丸质量m与摆块质量M的比值及弹丸的初速度v0。（取g=10m/s2，cos37°=0.8）

2. 如图5所示，上端固定着弹射装置的小车静置于粗糙水平地面上，小车和弹射装置的总质量为M，弹射装置中放有两个质量均为m的小球。已知M=3m，小车与地面间的动摩擦因数为μ=0.1。为使小车到达距车右端L=2m的目标位置，小车分两次向左水平弹射小球，每个小球被弹出时的对地速度均为v。若每次弹射都在小车静止的情况下进行，且忽略小球的弹射时间，g取l0m/s2，求小球弹射速度v的最小值。

解析：小球第一次被弹射时，规定小车的运动方向为正方向，

责任编辑 李平安