等级分制度在学生自助评价中的应用研究*
2017-04-07段旭良王曼韬
段旭良,王曼韬,穆 炯,周 蓓
(四川农业大学 信息工程学院,四川 雅安 625014)
等级分制度在学生自助评价中的应用研究*
段旭良,王曼韬,穆 炯,周 蓓
(四川农业大学 信息工程学院,四川 雅安 625014)
等级分制度是一种广泛应用于对弈比赛中评价选手能力的一种方法。本文在阐述了等级分评价机制的基本原理与常用算法的基础上,将基于贝叶斯推断的Glicko算法应用于实践性课程的学生自助评价中,把成绩评价的主体由教师单一个体转移到上课学生群体,具有开放、透明、多元、客观等特点。自助评价系统是学生进一步交流、借鉴和学习的平台,实际应用和实施中,学生参与度高,积极性大,态度认真;教学反馈及对评价结果分析表明,学生自助评价结果客观有效,有效地促进了教学质量的提高。
等级分;Glicko;教学;自助评价
一、引言
等级分制度是一种基于概率与统计的衡量对弈竞争中选手能力水平的评价方法,广泛应用于国际象棋、围棋、中国象棋、足球、篮球等运动中。等级分制度评价的基本原理是根据对弈选手的等级分(Rating),分别计算每人的期望获胜概率,根据期望概率与实际的一局或一轮比赛的结果(胜、负、平局),对参赛选手的等级分进行调整。一般而言,某选手的期望胜率越大,获胜后的等级分增量值越小,而对弈失败,等级分会有较大幅度的缩减;反之,若选手胜率很小,对弈失败影响不大,一旦胜利,等级分会有较大的增值。
在实践性较强的课程教学中,学生成绩的评定一般由教师根据作业或课程设计进行主观评价,由于个人知识与时间的限制,难以做到完全客观,且工作量较大;另一方面,传统评价过程对学生几乎是不透明的,由于缺乏交流与交互,学生得高分的期望动力不足,过关心态泛滥,作业或设计的对学习的促进效果也在一定程度上打了折扣。
为了改善教学的评价效果,广大一线教师和科研学者在学生课程评价理论、方法、指标体系、系统建设等方面做了大量有意义的探索,如对于网络环境下同伴匿名评价的理论和方法的实证研究、基于发展性评价理念的网络学习评价系统的设计,对评定方法、效果、评定模型等进行了研究[1-2];部分计算机课程中采用基于ACM(ACM国际大学生程序设计竞赛)的竞赛模式,对学生实验、作业进行全自动评价,取得了较好的实践效果[3-4]。
本文介绍了基于Glicko-2等级分评价算法在学生成绩自助评价中的应用,将等级分评价机制与学生成绩自助评价结合起来,基于一对一比较,计算学生作业,设计等级分,最后根据等级分折算成绩,评价过程完全透明。自助评价系统测试及在《网站建设与管理》课程作业设计的应用实践表明,自助评价结果合理可靠,学生参与性高,积极性大,取得了很好的效果。
二、等级分评价机制
1.Elo与国际象棋的等级分制度
20世纪50年代,匈牙利裔美国物理学家、美国国际象棋协会(USCF)大师级棋手Arpad Elo基于统计理论对当时的等级分评价系统进行改进,提出“Elo Ranking System”的等级分评价机制。1960年,美国国际象棋协会采用Elo Rating System作为其评分系统,1970年被国际棋联(FIDE)正式采用,此后,以Elo系统为基础的评价方法逐渐成为对弈水平评估的公认的权威方法。[5-9]
Elo模型最早使用正态分布,但是实践显示棋手的表现并非呈正态分布,现在的等级分计分系统通常使用的是对数分布。Elo的等级分更新机制非常简单,基本原理为根据胜率与一局比赛结果更新等级分。假设对手A、B当前等级分为RA、RB,则基于对数分布的A对B和B对A的期望胜率值EA、EB分别为[8]:
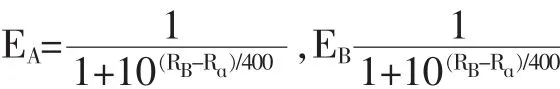
比赛完成后,根据选手在比赛中的得分SA(胜=1分,平=0.5分,负=0分)和期望胜率E更新等级分:
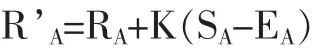
其中R’A为选手A新的等级分;K为参数,K越大,每次比赛完成等级分改变幅度越大。K一般根据选手等级分或参赛次数作相应调整,分数越高、参赛次数越多说明选手的能力越稳定,对应的K越小。例如在互联网国际象棋俱乐部(ICC)的规则中,根据选手等级分决定K值大小:
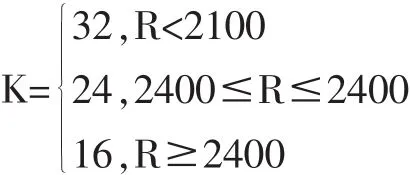
2.Glicko与微软TrueSkillTM、TopCoder评级算法
等级分评价系统历史上另一个具有里程碑意义的是1993年哈佛大学统计系博士Mark E.Glickman在其博士论文中提出的一种基于贝叶斯推断的“Glicko Rating System”[10]。当前,USCF、FIDE、Chess.com都采用Glicko或者其改进算法作为等级分评价系统。[11]
Glicko评价系统算法相对于Elo改进之处首先是等级分的更新不一定每次比赛后都要进行更新,而可以是某一阶段一系列比赛完成之后根据选手的综合表现更新等级分;其次,在计算等级分的同时计算评级偏差(Rating Deviation),用以更精确的说明选手的实际水平在等级分前后某一范围之内;在之后的改进版Glicko-2评价系统中,又引入了评级波动(Rating Volatility)值的计算,用以说明选手表现的稳定程度。[12]
近年来,Glicko系统除了在一对一比较(Paired Comparison)模型中得到广泛应用之外,还被众多学者以其为基础研究改进用于处理多人、多组竞赛的等级分评价模型,典型的有微软研究院开发的用于Xbox 360多人游戏、对手自动匹配模型的基于贝叶斯推断的TrueSkillTM算法。还有专门组织计算机程序设计竞赛的公司TopCoder采用的多人竞争评级的TopCode’s Rating Algorithm。[13-18]
三、Glicko及Glicko-2评价系统
1.Glicko等级分评价系统基本原理
Glicko和Glicko-2都是Mark Glickman博士在Elo系统基础上进行改进,提出的用于对弈比赛选手等级分评定的算法。在Glicko算法中,引入RD(Ratings Deviation,评分误差)作为衡量评级可靠性和精确性的一个指标。例如,某选手等级分Rating=1600,RD=50,那么该选手真实能力95%的等级分置信区间为 [Rating-2RD,Rating+ 2RD],即我们有至少95%的把握说明该选手的真实能力处在[1500,1700]这个区间中。[10、12、16-17]
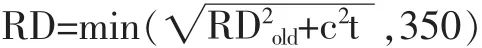
其中RDold为比赛选手最近一次比赛后的RD值,t为最后一次比赛距离现在的间隔周期,如当前正进行第5轮比赛,选手上一次参加比赛是在第2轮,则t=3,由此参数值的设定可以发现,选手间隔一段时间未参加比赛,则其评价的不确定性RD会随着时间推移而逐渐增大。式中c为常数,其大小决定RD值随时间变化增大的程度。
(2)计算并更新等级分
假设选手当前的等级分值为r,评级偏差为RD,这轮比赛有m个对手,等级分分别为r1,r2,…,rm,偏差分别为RD1,RD2,…,RDm,当前选手的每次比赛得分分别为s1,s2,…,sm,其中si值为1(胜)、0(负)、0.5(平)。按如下公式计算本轮比赛结束后选手的Rating和RD值:
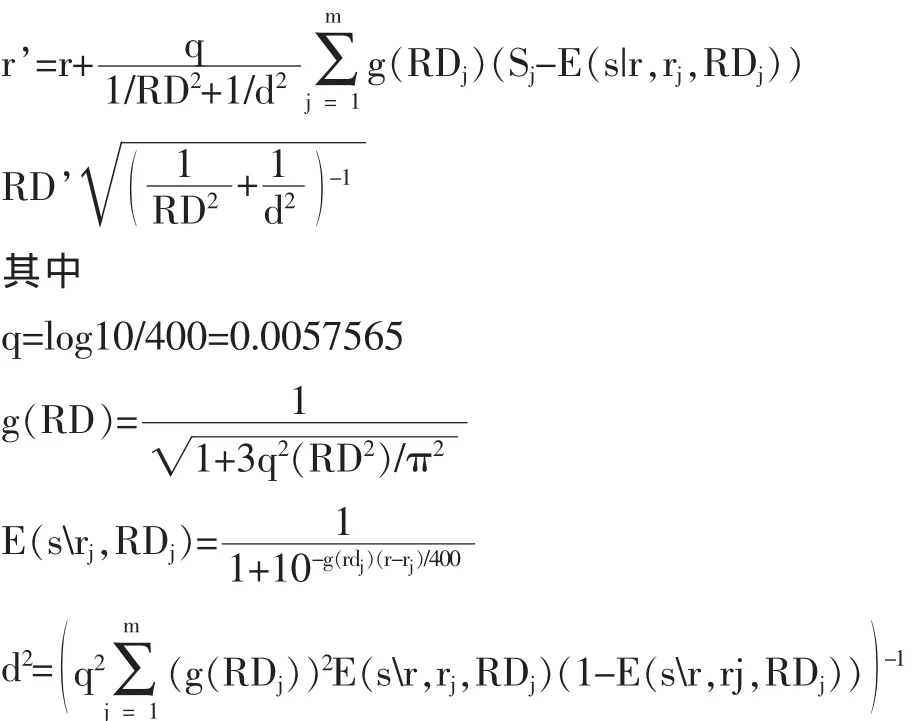
Glicko系统推荐选手每参加5-10场比赛 (一轮比赛,一个评分周期)更新一次等级分值,等级分的更新,主要有两步,确定RD值,计算并更新等级分。主要计算过程及说明如下:[12]
(1)确定参赛选手的本局比赛的RD值
2.Glicko-2等级分评价算法
Glicko-2算法在Glicko基础上,进一步引入了评级波动参数σ(Rating Volatility)变量,表示选手期望评级的波动情况,选手表现不稳定时σ较大,反之,值很小。与Glicko类似,每位选手具有r、RD以及σ三个属性,每周期(推荐至少10-15轮比赛)比赛结束后更新这三个值。需要注意的是,运算中r、RD需进行折算成Glicko-2过程变量,计算完成后再将结果折算为与Glicko相当的r、RD值。[17]
四、Glicko在课程教学自助评价中的应用
1.等级分制度在教学自助评价中的应用
在教学过程中,尤其是实践性较强的课程考核与评价中,成绩和作业的评定是一个既要耗费大量时间、精力,又难以做到完全客观、透明的过程。笔者曾尝试在课程实践和设计中引入问卷调查的投票方法进行评价,但是实际投票过程非常难以控制,很难要求学生浏览完所有设计后做出客观选择,并且,尽管采用了众多技术手段限制投票,但拉票等现象仍难以禁绝,评价结果可靠性不高。
应用两两比较的Glicko等级分评价机制,基于Web通过对随机出现的两件作业作品进行评价,其优势主要体现在以下几个方面:
(1)评价趣味性高且非常容易做出选择。每次浏览和比较的仅有两件作品,做出“哪个更好些”的选择非常容易,极大地简化了评价难度;
(2)提高了评价的客观性。同时,由于对弈作品完全随机出现,评价者评价自己作品或特定拉票作品的概率很低,或者可以采用技术手段避免评价自己,基本上避免了拉票现象,提高了评价的客观性和公正性;
(3)评价结果实时更新,过程完全透明。基于Web的评价系统其评价原则、结果和过程都是完全透明,参与者在公开的环境中评价、品评他人作品,是一个互动和相互学习的过程,并且动态更新的结果会给参与者带来一定的压力,在对待作业的态度上会更加重视,作品质量上会有所提高,更有效的提升了教学效果。
本文以Glicko-2评价机制在 《网站建设与管理》课程学生自助评价系统中的应用,阐明系统的建设、实施、控制过程及评价效果的分析。
2.自助评价系统的建设与算法参数
本研究应用ASP.NET开发实现了基于Web的自助评价系统,主要实现以下功能:
(1)评价用户的验证,基于学号和密码对用户进行验证。用户验证的目的有两个,一是通过类似实名认证的方式,记录每个人的每次投票,相比匿名方法能更好地避免不负责任的选择;二是整个评价过程亦作为教学过程的一部分,每人必须至少完成一定数量的投票。
(2)基于两两比较的评价。为了便于比较和选择,采用“iframe”框架技术将两件待评价网页显示在同一页面中。对弈作品的选择策略,可采用完全随机选择,或随机选择一件作品,根据其Glicko算法的Rating和RD值匹配水平相当的对手。本系统为了保证评价的均衡性,避免过多或过少评价,每次选择,均以作品的等级分更新次数升序排列(即作品参与评价的比赛轮数,而不是简单的比赛次数),在前十位中随机选择两件。这种选择方法一方面平衡了评价次数,另一方面每次选出的对手都是参与比赛数量比较接近的,相较完全随机选择方法更为合理。
(3)评价结果的展示。以“排行榜”的方式,依评价等级分从高到低依次显示列表,点击链接可浏览对应学生的网站作品。
系统的参数均按Glicko-2算法推荐设置,每轮比赛包括10局,即每位选手作品每被评价满10次更新一次等级分、偏差和波动值;等级分随时间变化常数τ=0.6;初始时,令所有r=1500,RD=350,σ=0.06。
3.学生实验、作业自助评价实施与控制
(1)作品的提交与评价
首先在服务器端配置好Web、FTP服务器。为方便程序处理,作品严格按规定的目录、文件命名和组织方法,在规定时间内提交到指定目录。例如作品目录必须以学号命名,首页文件必须命名为index.html/php/aspx等。完成后将作业目录映射为Web服务器虚拟目录,保证可通过Web访问到每件网站作品。
作品的评价时间为一周,一周之内任何时间均可上网进行评价,规定每人至少评价30次,最多评价200次。
(2)评价过程的控制
评价系统记录每一次评价的结果,包括评价人、评价IP、评价时间,作品1学号,作品2学号,是否作品1胜出等信息。
记录“是否作品1胜出”的主要目的是检测和发现不负责任的评价。两件随机选择的作品比较时,作品1一直在左侧,如果机械的完成任务,一直点击左侧胜出或者很有规律的“左右左右”的话,则结合每次评价的时间间隔,通过此人的评价序列中“是否作品1胜出”这一列很容易发现这一点。一旦确认存在此种情况,将及时在评价系统中公示并采取适当的惩戒措施。
记录每一次评价结果的另一目的是最大限度地避免不负责任的评价带来的影响,发现恶意评价后,可以及时排除干扰,根据评价历史对等级分进行重建。
系统采取的另一限制投票的手段为投票达到一定次数(如50次)后,强制退出并重新进行用户验证,避免恶意临时利用他人信息或软件自动投票。
4.测试与讨论
为了评价算法在自助评价中的稳定性和可靠性,通过模拟数据测试和实际课程评价两种方案对算法进行验证。
模拟数据以一个实际的教学班为基准,生成序号为1-76的总计76条数据,每条记录的数据项包括序号、Glicko算法Rating值、RD值等、比赛轮次、对比次数等,初始值均按默认参数设定。基于Glicko等级分原理,首先随机选择处一条记录A,再从与A的Rate值、轮次等信息在一定阈值范围之内的剩余记录中随机选择另外一条记录B,比较A、B的序号大小,大者为胜,记录结果。考虑到学生实际互评中不同人的标准不一,也可能有个别同学敷衍应付,测试中考虑了随机选择的因素,分别测试了无随机、有5%的随机选择、10%随机选择……60%随机选择对结果的影响。由于在等级分制度中,选手真实实力95%的置信区间为等级分值前后两倍偏差值(RD)的区间,单纯的Rating评分值的精确比较意义不大,所以对结果的评价按记录序号平均分为4组,即1-19,20-38,39-57,58-76,按Rate值升序排列,前19条记录中出现序号大于19的记作错误,20-38条记录中出现序号小于20或大于38的记作错误,依此类推,每组记录中总错误数与记录数比值即为错误率。测试分两轮进行,第一轮测试平均每条记录被比较100次,第二轮测试平均每条记录被比较20次,测试结果如图1所示。
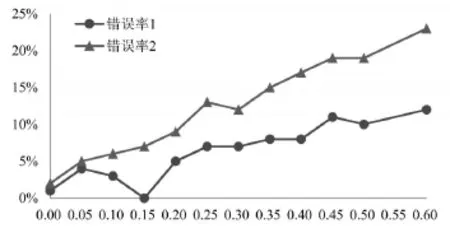
图1 不同随机选择、不同比较次数下错误率情况
图中横坐标轴表示无视序号大小进行随机选择的概率,纵坐标轴表示错误率 (错误率=错误数/记录数*100%),错误率1由第一轮测试产生,错误率2由第二轮测试产生。对比分析显示,同样概率的随机选择下,单位记录评价次数越高,错误率越低;随着随机选择概率的逐渐增大,错误率呈上升趋势。值得注意的是,第一轮测试中,当随机选择概率高达0.5时,也就是允许一半学生完全随机评价时,错误率依然稳定在10%左右,这表明基于等级分制度的自助评价机制有较强的抗干扰能力和稳定性。
实际课程的学生自助评价以《网站设计与管理》(推选课)课程作业设计为例。采用Glicko-2等级分评价机制进行透明公开的Web自助评价,总计收到合格的作业作品76份 (另有7份作品命名或文件组织不符合要求,未参与自助评价),开放评价时间为8天。总计9421条有效评价记录,每学生最多评价200次,最少的评价了17次,人均114次,远高于30次的下限要求,学生表现出较高的积极性。
每件作业作品参与评价次数最高128,最低121次,平均被评价124次,至多相差评价次数不大于一个等级分更新周期。数据分析中也发现,RD值普遍偏大。RD反映的是评级的偏差程度,选手真实实力95%的置信区间为等级分值前后两倍偏差值的区间,RD值偏大,导致反映其真实实力的区间也偏大,从这个意义上来讲,等级分相差几分甚至十几分,排名相差几名的差别是不大的。产生这种现象的原因主要是每个人的评价标准是难以统一的,有的评价者更看重美观性,有的评价者更看重内容,而有的评价者把原创性作为决定胜负的唯一标准。所以RD值偏大是正常的,从一个侧面反映了评价系统的透明性、公开性、多元化的评价准则,在一定程度上也更为客观的反映了作品的实际水平。在评价结果的方面,经过对等级分排行榜中前20人、中间20人、后20人以及部分随机抽查的作业进行检查来看,结果也是科学有效的,排在前面的作品在原创性、美观性、内容的丰满程度等方面有很好的平衡,等级分较低的作品基本内容简陋、或原创性低。
总之,通过以上数据分析可以发现,基于Glicko-2的自助评价系统抗干扰能力强,稳定性好,结果可靠;从实际课程评价次数和每天的评价分布情况来看,这种竞争机制激励了学生的热情,评价者表现出了较高的积极性,评价结果可以反映学生实际的作业完成情况。
五、结束语
评价结果分析显示,基于Glicko-2等级分评价算法自助教学评价系统具有开放性、透明性、客观性等特点,评价数据客观合理,结果可靠,可以真实的反应学生作业设计完成的实际情况。
[1]吕啸,余胜泉,谭霓.基于发展性评价理念的网络教学平台学习评价系统设计[J].电化教育研究,2011(2):73-78.
[2]张倩.网络环境下同伴匿名评价实证研究[J].电化教育研究,2007(7):55-57,71.
[3]吴川,孙锦程.基于ACM的《算法设计与分析》教学改革研究[J].中国科教创新导刊,2010(32):62.
[4]杨春明,陈念年.基于竞赛模式的“算法分析与设计”教学探索与实践[J].计算机教育,2009(20):146-147,105.
[5]GLICKMAN M E,JONES A C.,Rating the chess rating system[J].Chance.1999(12)2:21-28.
[6]GLICKMAN M E.A comprehensive guide to chess ratings[J].American Chess Journal 3(1995),59-102.
[7]Wikipedia.Chess rating system[EB/OL].http://en. wikipedia.org/wiki/Chess_rating_system.
[8]Wikipedia.Elo rating system[EB/OL].http://en. wikipedia.org/wiki/Elo_rating_system.
[9]REMI C.Computing Elo ratings of move patterns in the game of go[J].ICGA Journal January.2007(7):113-124.
[10]GLICKMAN M E.Paired comparison models with time varying parameters,Ph.D.thesis[D],Harvard University Dept of Statistics,1993.
[11]Wikipedia.Mark Glickman[EB/OL].http://en. wikipedia.org/wiki/Mark_Glickman.
[12]GLICKMAN M E.Parameter estimation in large dynamic paired comparison experiments[J].Applied Statistics 48(1999),377-394.
[13]Microsoft.TrueSkill?ranking system FAQ-Microsoft Research[EB/OL].http://research.microsoft.com/enus/projects/trueskill/faq.aspx.
[14]Microsoft.TrueSkill?:A Bayesian skill rating system[J].MIT Press.2007.
[15]TopCoder.Algorithm competition rating system [EB/OL].http://apps.topcoder.com/wiki/display/tc/Algorithm+Competition+Rating+System.
[16]GLICKMAN M E.The Glicko system[EB/OL]. http://www.glicko.net/glicko.html.
[17]GLICKMAN M E.Example of the Glicko-2 system[EB/OL].http://www.glicko.net/glicko.html.
[18]FORISEK M.Theoretical and practical aspects of programmingcontests.PhDthesis[D].ComeniusUniversity.
G434
A
1673-8454(2017)05-0061-05
四川省教育厅项目自然科学一般项目(15ZB0017);四川农业大学校级教改项目(X2015043)。
