章动面齿轮传动的啮合原理与动态仿真
2017-04-06王广欣邓佳王朋李林杰
王广欣,邓佳,王朋,李林杰
(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.中国中车齐齐哈尔轨道交通装备有限责任公司,黑龙江 齐齐哈尔 161002) *
章动面齿轮传动的啮合原理与动态仿真
王广欣1,邓佳1,王朋1,李林杰2
(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.中国中车齐齐哈尔轨道交通装备有限责任公司,黑龙江 齐齐哈尔 161002)*
根据啮合原理推导内切面齿轮的齿面方程、啮合方程和界限条件,以及内切面齿轮与外切面齿轮啮合的共轭条件,构成共轭啮合的“面-面”齿轮副,结合章动原理提出新型章动面齿轮传动.根据推导的面齿轮齿面方程,利用Pro/E软件构建章动面齿轮传动的三维模型,并采用ADAMS软件对其进行动态啮合力仿真,分析了新型章动面齿轮副动态啮合力的变化规律,为传动装置的优化设计及动力学分析提供了参考依据.
章动传动;齿轮;仿真
0 引言
面齿轮传动是一种圆锥齿轮(面齿轮)与直齿圆柱齿轮相啮合的传动[1-3],具有重合度大,振动小,噪声低的优点,在高速、重载的情况下有很好的应用.章动齿轮传动是一种将章动原理应用于齿轮传动的新型传动[4-6],具有传动平稳、结构紧凑、承载能力强和效率高等优点,可应用于冶金、矿山和石油化工等各类机械中.章动面齿轮传动综合了章动齿轮传动和面齿轮传动的优点[7],在直升机、盾构机等大功率领域具有良好的应用前景.
为实现章动面齿轮传动中“面-面”齿轮副的共轭啮合,本文结合面齿轮的加工原理给出“内切”面齿轮齿面形成条件并研究了“内切”面齿轮的齿面形成.由于齿轮传动中轮齿的啮合冲击往往是导致齿轮传动振动、噪音和点蚀破坏的主要原因[8-9],获取章动面齿轮传动中轮齿接触力的变化规律具有重要的意义.因此,进行传动的动态受载研究.
1 结构原理
章动面齿轮传动的基本组成结构主要包括输入轴、固定面齿轮、行星面齿轮和转动面齿轮,图1是基本型章动面齿轮传动的机构简图.图中,固定面齿轮与机架固连,输入轴的轴线与行星面齿轮所在倾斜轴段处轴线的夹角为章动角β. 根据硬币的章动现象可知,若将行星面齿轮左侧轮齿看作硬币,固定面齿轮看作桌面,则当输入轴转动一周时行星面齿轮左侧轮齿会绕自身轴线转过一个转角;同理,若将行星面齿轮右侧轮齿看作硬币,转动面齿轮看作桌面,则当输入轴转动一周时行星面齿轮右侧轮齿也会绕自身轴线转过一个转角;由于行星面齿轮两侧轮齿是一个整体,故二者之间必然存在“转角差”,当行星面齿轮与转动面齿轮啮合时,会将这个“转角差”传递给转动面齿轮,从而实现动减速运动.
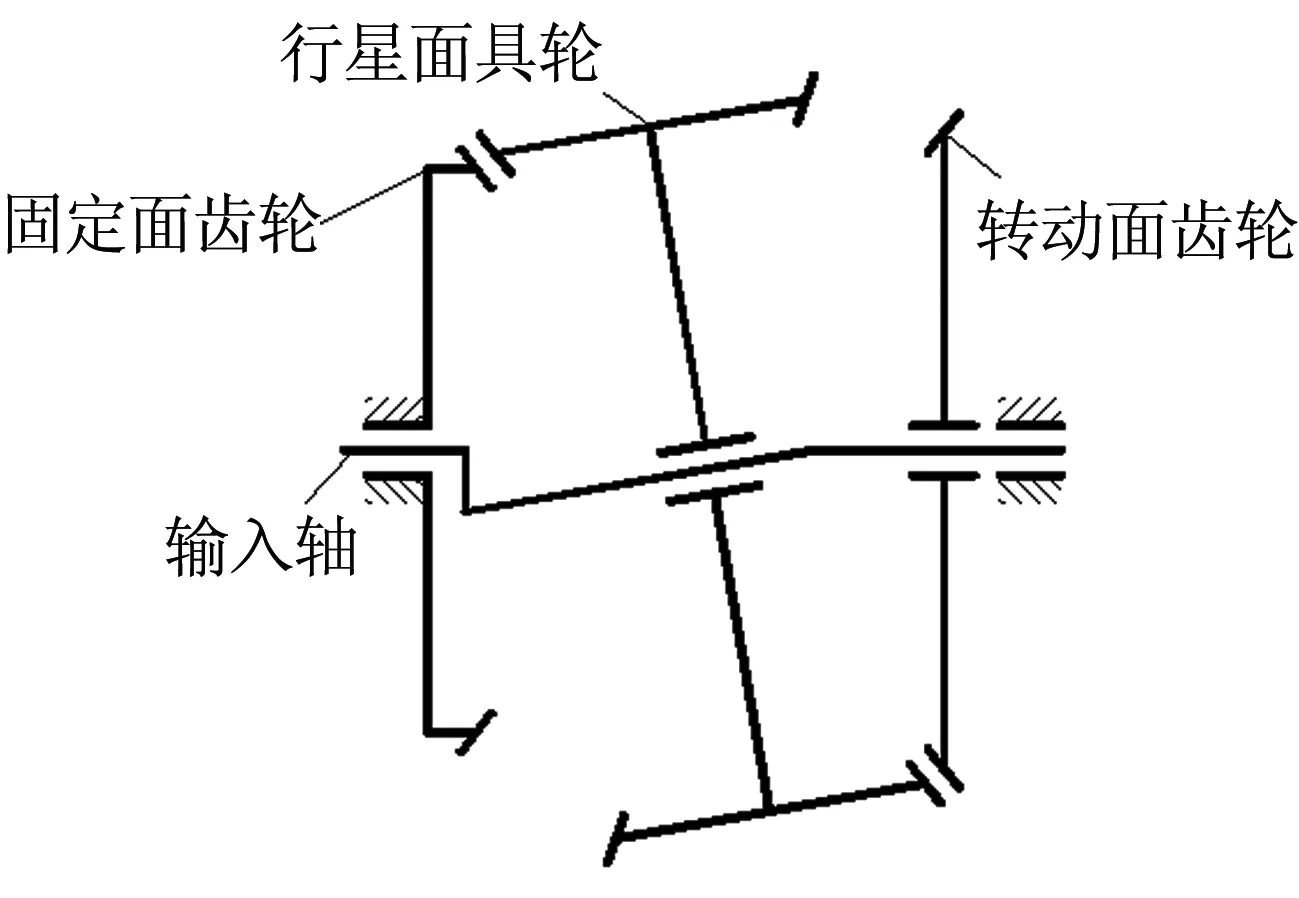
图1 章动面齿轮装置结构简图
根据章动传动原理设计两对共轭啮合“面-面”齿轮副,得到章动面齿轮传动装置的结构简图,如图2所示.,这里对“面-面”齿轮副不作解释,在下一节将作具体介绍.
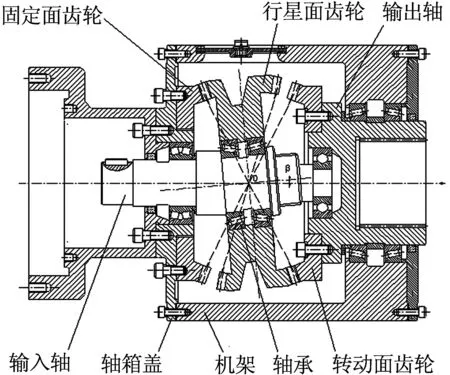
图2 章动面齿轮装置结构简图
由图2可知,固定面齿轮上的z1个齿与行星面齿轮左侧的z2个齿构成“面-面”啮合副,行星面齿轮右侧的z3个齿与转动面齿轮上的z4个齿构成“面-面”啮合副.当输入轴以恒定角速度转动时,带动行星轮作章动运动,行星轮在两侧“面-面”齿轮副的作用下,将运动与转矩传递给转动面齿轮,从而实现减速传动.
2 齿面形成
2.1 “内切”面齿轮形成原理
传统面齿轮传动中,面齿轮的加工是通过刀具(渐开线直齿轮)直接外切得到的,可称为“外切”面齿轮.根据齿轮啮合原理可知,这样直接得到的两个面齿轮是无法共轭啮合的.在章动齿轮传动中,为保证共轭啮合,形成章动面齿轮副,须采用与真实刀具结构参数相同的假想刀具加工“内切”面齿轮.如图3所示,这时假想刀具的齿面外法矢方向与真实刀具的内法矢方向相同,这样得到的面齿轮就是内切面齿轮.
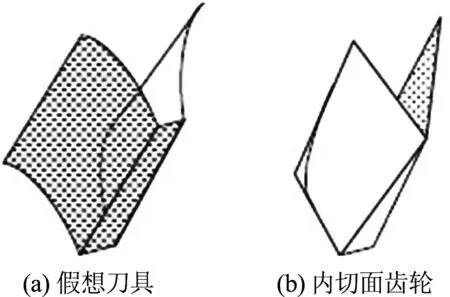
图3 假想刀具与内切面齿轮的啮合面
这样由同一刀具加工得到的外切面齿轮与内切面齿轮可共轭啮合,即构成“面-面”齿轮副. 这里,固定面齿轮和转动面齿轮是外切面齿轮,行星轮两侧轮齿采用内切面齿轮齿形,则固定面齿轮和转动面齿轮各自与行星面齿轮两侧轮齿构成“面-面”齿轮副.为了便于研究,把固定面齿轮定义为面齿轮1,行星轮在固定面齿轮侧和转动面齿轮侧分别定义为面齿轮2和面齿轮3,转动面齿轮定义为面齿轮4.
如图4所示,β1和β2分别为面齿轮1和面齿轮2的节锥角,γs为刀具的节锥角,γ1为面齿轮1和刀具的轴间角,γ2为面齿轮2和假想刀具的轴间角,面齿轮1与面齿轮2共轭啮合时其节锥和节锥顶点重合.
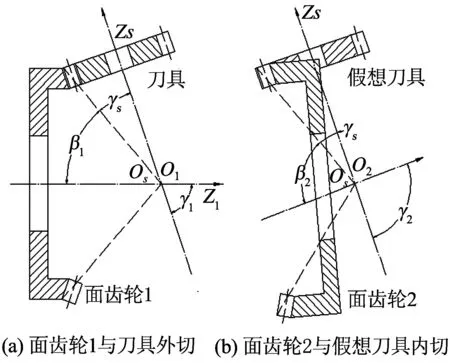
图4 刀具与面齿轮啮合示意图
为保证刀具与面齿轮1外切,而假想刀具与面齿轮2内切,其轴间角和节锥角需满足下列条件[10]:
(1)
给定面齿轮和假想刀具的齿数以及章动角,根据式(2),即可求出β1、β2、γs、γ1和γ2.
(2)
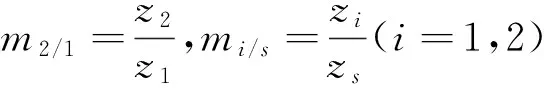
结合仿真算例,给定面齿轮和假想刀具的基本参数,如表1和表2所示.
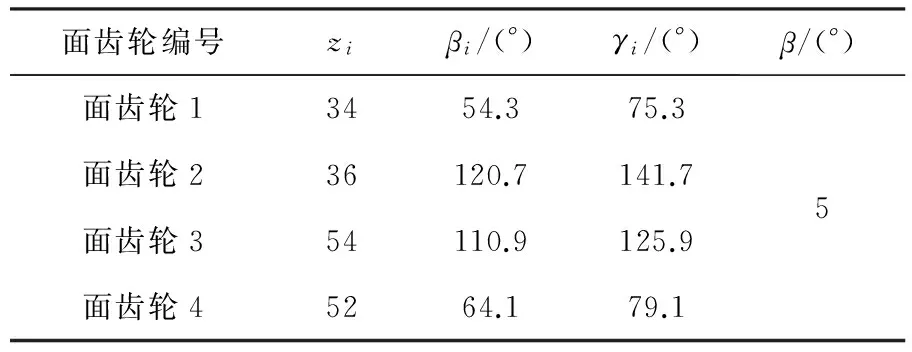
表1 面齿轮的基本参数

表2 假想刀具的基本参数
2.2 内切面齿轮齿面方程和啮合方程
根据空间啮合原理[11]建立如图5所示的空间坐标系,其中S20(O20,X20,Y20,Z20)是与内切面齿轮相固连的固定坐标系,S0(O,X,Y,Z)是与假想刀具相固连的固定坐标系,S2(O2,X2,Y2,Z2)是与内切面齿轮相固连的动坐标系,Ss(Os,Xs,Ys,Zs)是与假想刀具相固连的动坐标系.上述四个坐标系的坐标原点重合,且Z20轴与Z2轴重合,Z0轴与Zs轴重合,Zs轴与Z2轴之间的夹角为γ2,则γm2=180°-γ2,φ2角为内切面齿轮的瞬时转角,φs为假想刀具的瞬时自转角,β为章动角.本文中坐标系遵循右手定则,取右手的螺旋方向为正方向.
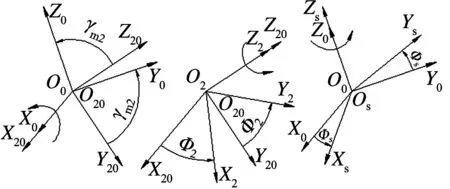
图5 各坐标系之间的关系
由坐标系Ss到坐标系S2的变换矩阵M2s为:
(3)
式中,b11=cosφ2cosφs+sinφ2cosγm2sinφs
b12=-cosφ2sinφs+sinφ2cosγm2cosφs
b13=-sinφ2sinγm2
b21=-sinφ2cosφs+cosφ2cosγm2sinφs
b22=sinφ2sinφs+cosφ2cosγm2cosφs
b23=-cosφ2sinγm2
b31=sinγm2sinφs
b32=sinγm2cosφs
b33=cosγm2
已知假想刀具的齿面方程rs(θs,us)为:
(4)
式中,rbs为假想刀具的基圆半径,θs0为假想刀具轮齿对称线到渐开线起始点的角度,θs为假想刀具渐开线上任一点的角度,us为假想刀具上任一点的轴向参数,xs、ys和zs分别是假想刀具上任一点在x轴、y轴和z轴上的坐标.
由式(3)和式(4),整理可得内切面齿轮的齿面方程r2(us,θs,φs)为:
(5)
式中,x2、y2和z2分别是内切面齿轮上任一点在x轴、y轴和z轴上的坐标.
根据空间啮合原理[11],可推得假想刀具与内切面齿轮的相对速度ν(s,2)〗为:
(6)
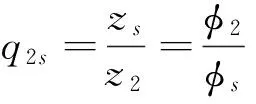
由此可推得假想刀具与内切面齿轮的齿面啮合方程为:
(7)
则假想刀具的轴向参数us可表示为:
(8)
2.3 内切面齿轮界限条件
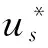
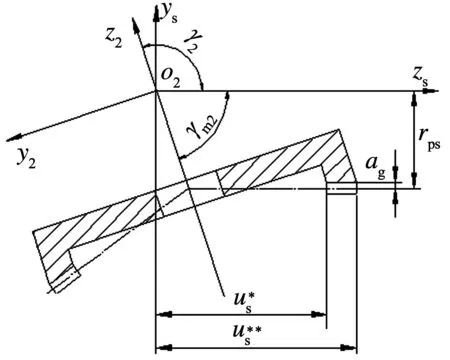
图6 内切面齿轮的限制尺寸
根据面齿轮不产生根切的条件[11],有如下关系式:
(9)

将式(4)、(6)和(7)整理后代入式(9),可得:
(10)
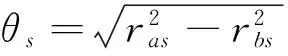
当内切面齿轮的齿槽变尖时,由图6可知,有如下关系式:
(11)
式中,rps是假想刀具的节圆半径,ag是假想刀具的齿顶高.
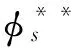

表 3 内切面齿轮的界限尺寸值
2.4 共轭条件
以面齿轮1和面齿轮2构成的面-面齿轮副为例,由于面齿轮1和面齿轮2是由同一刀具分别外切、内切形成,故刀具的轴向参数us需满足:
(12)
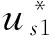
(13)
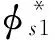
根据刀具与面齿轮1、假想刀具与面齿轮2的啮合方程,整理可得到共轭啮合时,刀具展角参数θs的取值范围为:
(14)
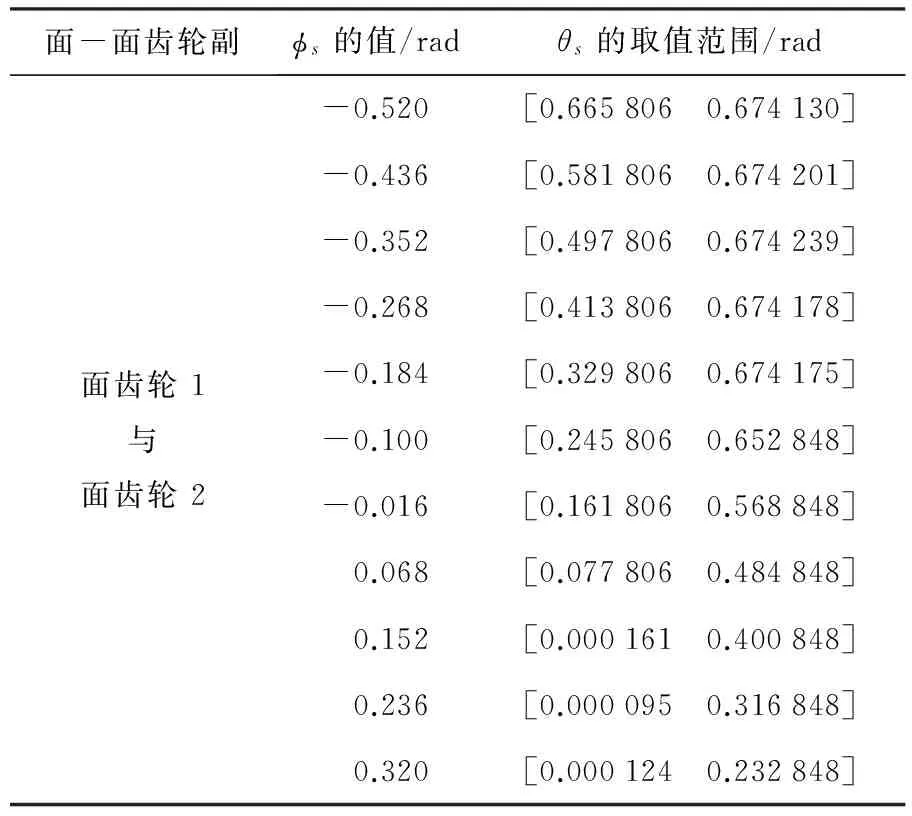
表4 刀具展角参数θs取值范围
根据表3列出实例的界限尺寸值,即可得到刀具展角参数θs的取值范围,具体如表4所示.
2.5 建立三维模型
根据表4中展角θs的取值范围,由式(5),即可求算例中面齿轮1和面齿轮2的齿面接触线,如图7(a)和7(b)所示.利用Pro/E软件,即可构建章动面齿轮传动装置的三维装配模型简图,如图7(c)所示.
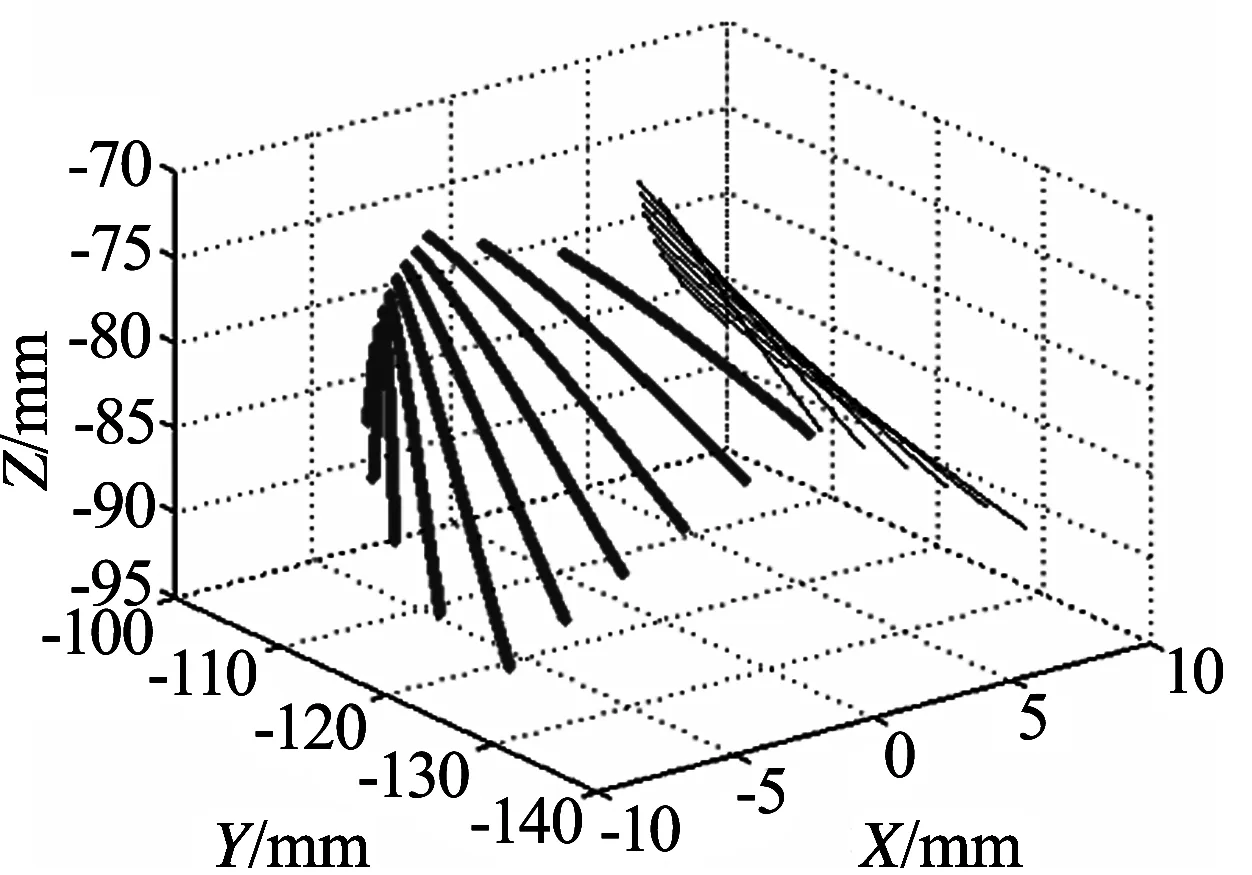
(a) 面齿轮1三维模型
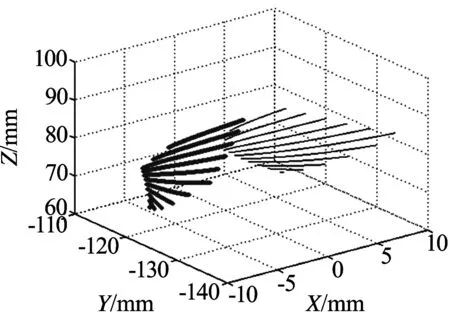
(b) 面齿轮2三维模型

(c) 章动面齿轮传动副的装配简图
3 仿真
3.1 仿真设置
以隧道掘进领域土压平衡盾构机主减速器作为应用目标,设计章动面齿轮传动减速器.其基本参数如下:传动比为52,功率为38kW,输入转速为n1=294.84r/m(1769.04°/s)[12].材料的具体属性见表5.
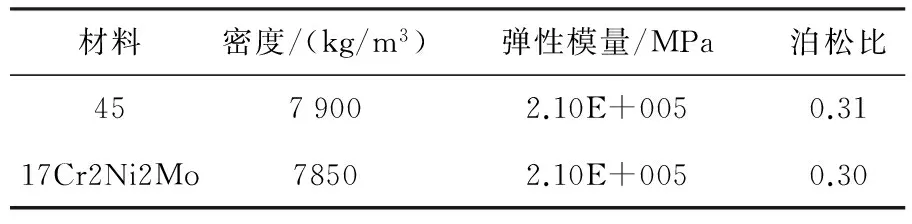
表5 主要零件的材料和材料属性
假设各零件都为刚体,将建立好的三维模型导入ADAMS中,设置零件的材料属性,并定义如下约束、驱动和载荷[13]:
(1)在固定面齿轮与地面之间建立固定副1;
(2)在输入轴与地面之间建立旋转副2;
(3)在转动面齿轮与地面之间建立旋转副3;
(4)在行星面齿轮和输入轴之间建立旋转副4;
(5)在固定面齿轮和行星面齿轮之间施加接触;
(6)在转动面齿轮和行星面齿轮之间施加接触;
(7)在旋转副2上添加驱动,输入角速度为1769.04°/s;
(8)在转动面齿轮上施加负载扭矩,负载扭矩为60 803.4 N/m.
将上述设置完成后,可得到章动面齿轮传动的虚拟样机模型.
3.2 仿真设置
章动面齿轮传动在传动过程中,面齿轮与面齿轮之间的接触力包括碰撞力和摩擦力,其中碰撞力在ADAMS中定义为[14]:
F_impact=
(15)
式中,STEP为阶跃函数,q0为两物体间初始距离,q为物体碰撞过程中的实际距离,q0-q为碰撞过程中的变形量,K为刚度系数,C为阻尼系数,e为碰撞指数项,d为渗透深度.而摩擦力定义为库伦摩擦力,主要参数有[15]:静滑移速度νs、动滑移速度νd、动摩擦系数μd和静摩擦系数μs,这些参数由经验值确定,如表6所示.

表6 接触力参数经验值表
3.3 仿真结果
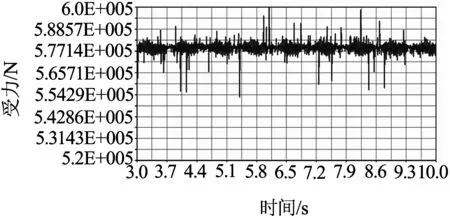
将仿真步数设为1 000,仿真时间设为10 s进行仿真,可得理想情况下固定面齿轮和转动面齿轮的动态受力曲线,如图8所示.
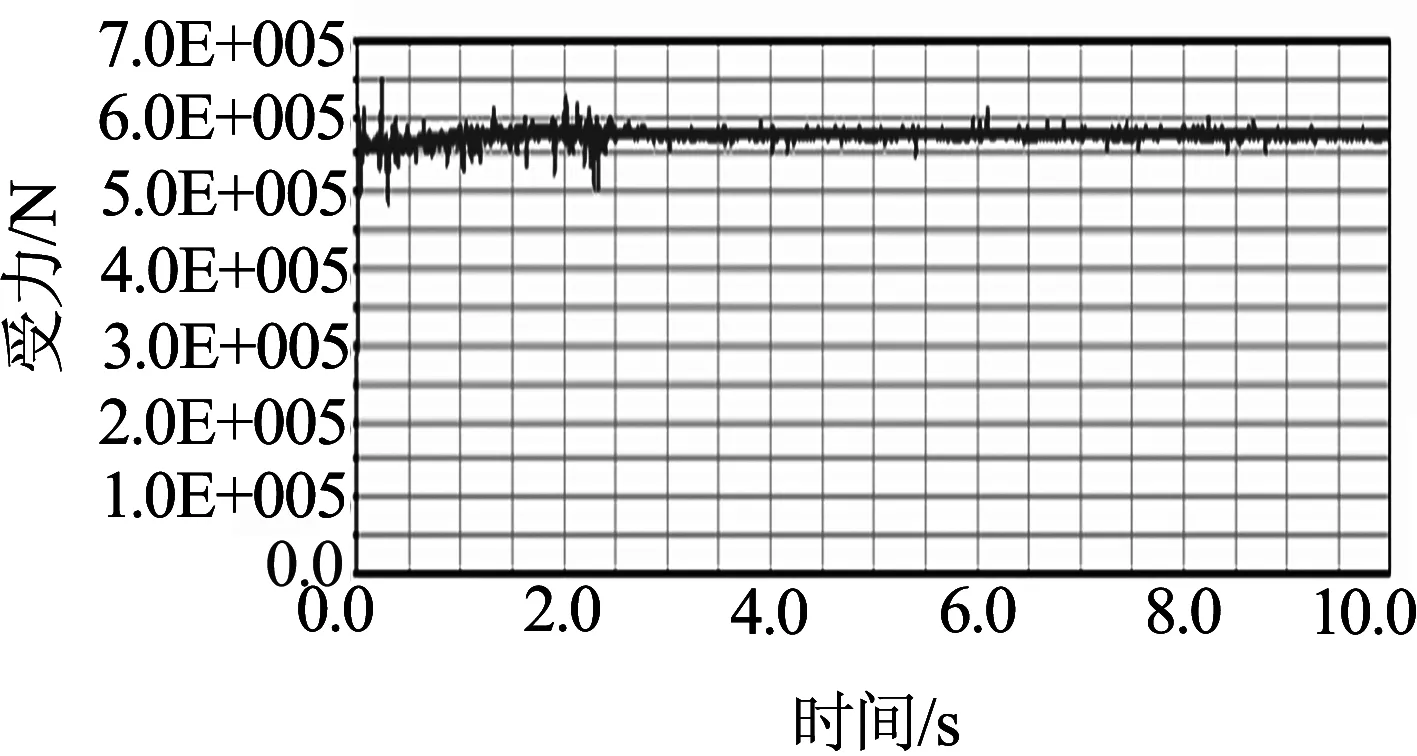
(a) 固定面齿轮
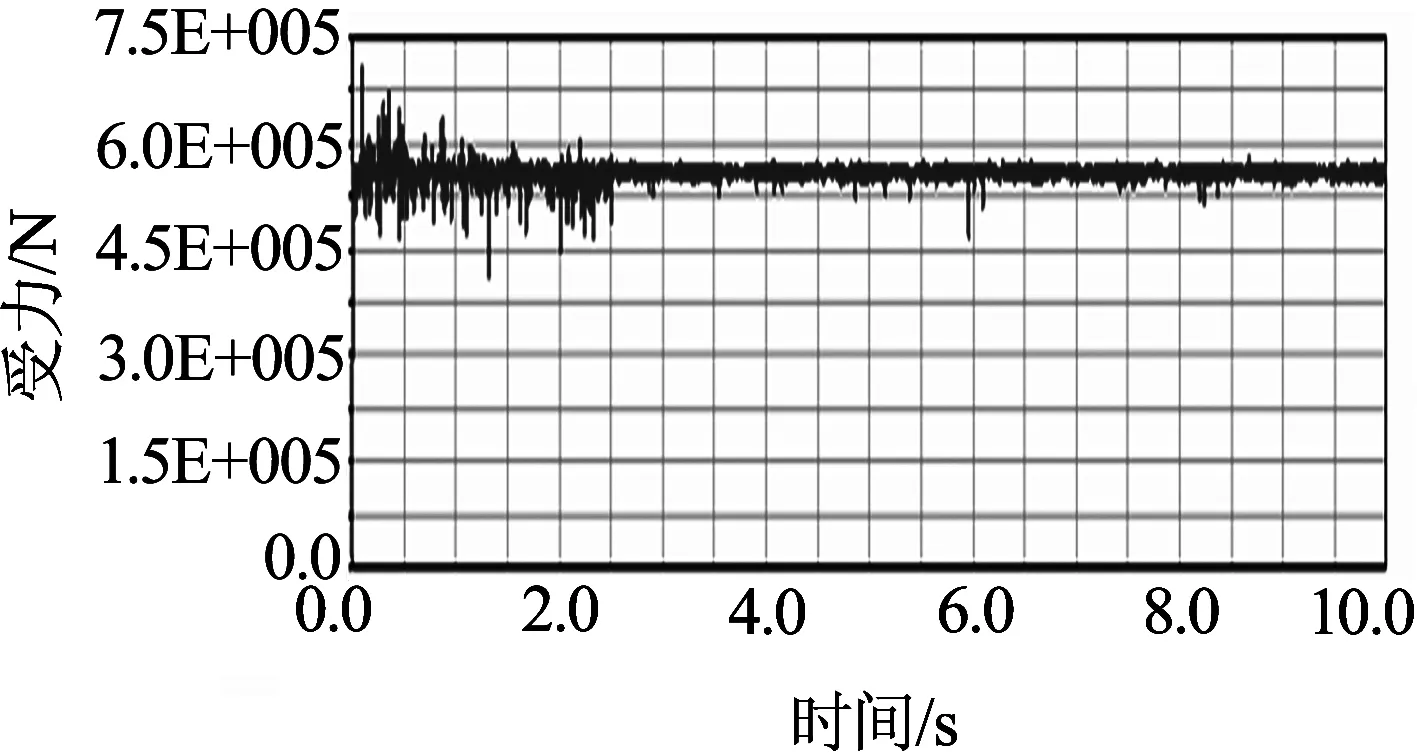
(b) 转动面齿轮
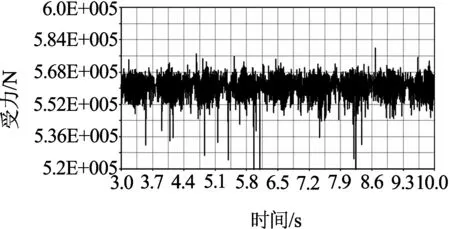
将图8(a)和8(b)中运动平稳后的曲线截取放大,可得到图9(a)和9(b) .
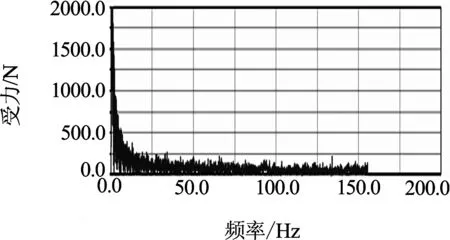
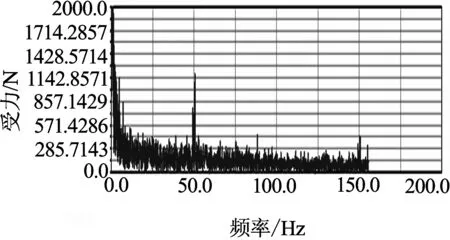
将图8(a)和8(b)中的曲线进行FFT变换,即可得到固定面齿轮和转动面齿轮动态受力的频谱曲线,如图10(a)和10(b)所示.
从图8(a)和9(a)中可以看出,对于固定面齿轮,刚开始啮合时,由于面齿轮与面齿轮间存在间隙,且假定面齿轮与面齿轮之间是刚体接触,所以啮合时其齿面接触力存在波动;随着啮合的进行,间隙消除,所以运动趋于平稳,波动明显减小;从平稳后的局部放大图可知,其平稳时的接触力变化具有周期性,变化周期大约为0.7s,波动幅度为0~8 572.5 N.
(a) 固定面齿轮
(b) 转动面齿轮
(a) 固定面齿轮
(b) 转动面齿轮
从图8(b)和9(b)中可以看出,对于转动面齿轮,刚开始啮合时,其接触力同样存在的波动,且波动比固定面齿轮大,这是由于转动面齿轮与行星轮间的碰撞力较大;运动平稳后,波动明显减小;从平稳后的局部放大图可知,其平稳时的接触力变化也具有周期性,变化周期与固定面齿轮接触力变化周期相同,波动幅度为0~17 600 N;与固定面齿轮相比,其受力周期性更强.
从图10(a)和10(b)中可以看出,固定面齿轮没有幅值突出的谱线,而转动面齿轮有2条幅值突出的谱线:一条是频率为50 Hz,它对应行星轮与转动面齿轮的啮合频率;另一条是频率为150 Hz,它对应行星面齿轮与转动面齿轮的3倍啮合频率.
4 结论
(1)本文将章动原理与面齿轮齿形结合,提出了章动面齿轮传动.根据齿轮啮合原理,推导出外切面齿轮与内切面齿轮构成“面-面”齿轮副的共轭啮合条件;
(2)根据推导的齿面构建章动面齿轮三维模型,应用ADAMS软件对章动面齿轮传动副的动态受力进行仿真.分析可知,齿轮副啮合过程中接触力的波动具有一定的周期性.行星轮和转动面齿轮之间接触力的波动更剧烈些,故失效更容易发生行星轮和转动面齿轮之间;章动面齿轮传动的啮合频率取决于转动面齿轮和行星面齿轮之间的啮合频率,与固定面齿轮和行星面齿轮之间的啮合频率关系不大.
[1]李晓贞, 朱如鹏, 李政民卿, 等. 非正交面齿轮传动系统的耦合振动分析[J]. 中南大学学报,2013,44(6):2274-2280.
[2]王延忠, 田志敏, 侯良威, 等. 正交面齿轮传动系统啮合动力学仿真[J]. 机械传动,2013, 37(11):57-60.
[3]徐伟俊, 彭学玉, 李清. 偏置面齿轮齿面方程和仿真[J]. 机械设计与制造,2013, (4):94-98.
[4]KEDROWSKI D K, SLIMAK S P. Nutating gear drive train for a cordless screwdriver [J]. Mechanical Engineering, 1994 (1): 70-74.
[5]WANG G X, ZHU L L, GUAN T M. Design and Simulation of the Nutation drive with Movable Teeth VDI-Berichte Nr. 2199[R]. International Conference on Gears 2013, 2013: 13-22.
[6] YAO LIGANG, GU BING, HUANG SHUJUAn. Mathematical Modeling and Simulation of the External and Internal Double Circular-Arc Spiral Bevel Gears for the Nutation Drive[J]. Journal of Mechanical Design, 2010, 132: 1-9.
[7]SARIBAY Z B, BILL R C. Design analysis of Pericyclic Mechanical Transmission system[J]. Mechanism and Machine Theory, 2013, 61: 102-122.
[8]黄中华, 张晓建, 周玉军, 等. 渐开线齿轮啮合碰撞力仿真[J]. 中南大学学报, 2011, 42(2):379-383.
[9]佟操, 孙志礼, 马小英, 等. 考虑安装与制造误差的齿轮动态接触仿真[J]. 东北大学学报, 2014, 35(7):996-1000.
[10]SARIBAY Z B. Tooth Geometry and Bending Stress Analysis of Conjugate Meshing Face-gear Pairs [J]. Journal of Mechanical Engineering Science, 2012, 227(6): 1301-1314.
[11]李特文(美), 国楷, 叶凌云, 等. 齿轮几何学与应用理论[M].上海:上海科学技术出版社, 2008.
[12]肖正明, 秦大同. 土压平衡盾构机主减速器三级行星齿轮系统动力学[D].重庆:重庆大学, 2011.
[13]陈立平, 张云清, 任卫群, 等. 机械系统动力学分析及ADAMS应用教程[M]. 北京:清华大学出版社, 2005.
[14]赵宁, 慧广林, 康士朋, 等. 考虑误差的行星齿轮啮合力仿真[J]. 计算机仿真,2010, 27(3):284-287+339.
[15]梁晶晶, 李瑞琴, 任家俊, 等. 基于UG及ADAMS的新型行星锥齿轮无级变速传动系统动态受载仿真研究[J]. 机械传动, 2012, 9(36):12-15.
Meshing Principle and Dynamic Simulation of Nutation Drive with Face-Gar
WANG Guangxin1, DENG Jia1, WANG Peng1, LI Linjie2
(1.School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028, China; 2.CRRC Qiqihar Railway Rolling Stock Co., Ltd, Qiqihar 161002, China)
According to the tooth surface equation, the meshing equation and boundary condition of internal face-gear and combining the conjugate meshing condition of external face-gear and internal face-gear, the internal face-gear and the external one may constitute “surface-surface” gear pair under the conjugate meshing, and a new nutation drives with face-gear was proposed based on the nutation principle. The establishment of the 3D model of nutation drives with face-gear using PRO/E software is introduced based on tooth surface equation of face-gear, and the meshing force simulation is executed by ADAMS software. The change rule of dynamic meshing force of the new type of nutation drives pairs with face-gear are analyzed. The results provide referential basis for the optimization design and dynamics analysis of the transmission device.
nutation drive; gear; simulation
1673- 9590(2017)02- 0048- 07
2016-04-01 基金项目:国家自然科学基金资助项目(50905021,51375063);大连市高层次人才创新支持计划资助项目(2015R072)
王广欣(1979-),男,副教授,博士,主要从事新型传动、运动与康复器械、机械动力学的研究 E- mail:wgx@djtu.edu.cn.
A
