城市轨道交通列车开行方案研究

马彩雯，石晶，徐燕秋

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

城市轨道交通列车开行方案研究

马彩雯，石晶，徐燕秋

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

通过以列车编组、最小时间间隔、列车上座率等为约束条件，建立以旅客出行成本最小和企业运营成本最小的非线性双目标整数规划模型，引入平均运距对乘客出行时间进行求解.通过对大连市快轨3号线主线开行方案的确定，来验证模型的合理性.计算结果表明，本模型得到的开行方案满足约束条件，符合旅客与企业双方的利益要求.

城市交通；开行方案；非线性整数规划；大小交路模式

0 引言

随着城市轨道交通的快速发展，城市轨道交通开行模式和列车种类越来越丰富，随之而来的列车开行方案日益受到重视.客流的不断增长与变化，使城市轨道交通列车开行方案需要随时间变化，分时段确定.狭义上的列车开行方案就是确定不同时段内需要开行的列车数.

在理论研究方面，文献[1]分析了大小交路模式下不同客流量的计算方法，引入分担率，同时以列车追踪间隔时间和车底数量为约束，构建了城市轨道交通大小交路模式下的列车开行方案模型.并运用理想点法将双目标转化为单目标，并使用lingo软件求解.文献[2]采用不同的约束条件，动车组数和企业运营效益，将乘客等待时间作为目标函数，构造模型，设计了基于二进制结构的特殊编码方法进行求解.

一般意义上，求解开行方案主要考虑的约束条件为列车编组、列车上座率、最小时间间隔、列车开行频率要求等，而作为目标函数的主要是客流的总出行费用最小、列车运营成本最小.在此基础上，本文研究的主要内容为：研究大小交路模式下，通过分担率的不同，引入平均运距，求解出旅客列车开行方案，并能保证符合约束条件，同时使乘客总出行成本和运输企业运营成本符合双方利益.

1 开行方案相关概念论述

本文研究基础为大小交路模式，故假定小交路开行对数为大交路对数的整数倍，且各区段客流都会被平均分摊，以此来确定大小交路客流分担率.

大小交路模式如图1所示，设轨道交通线路S={si|i=1,2，…，a}为车站集合，其中在S到Sa开设大交路列车，在S到Sb站开行小交路列车.

城市轨道交通运行时段集合为T，Ti为时段i的时长，大交路开行数记为di，小交路开行数是大交路的m(m为整数)倍，设交路中全日总客流量为P总，根据假设，可知客流被大小交路列车平均分担，则大交路客流分担率为β1=1/(1+m)，小交路分担率为β2=1-β1.列车编组长度记为Q，列车载客能力记为N.

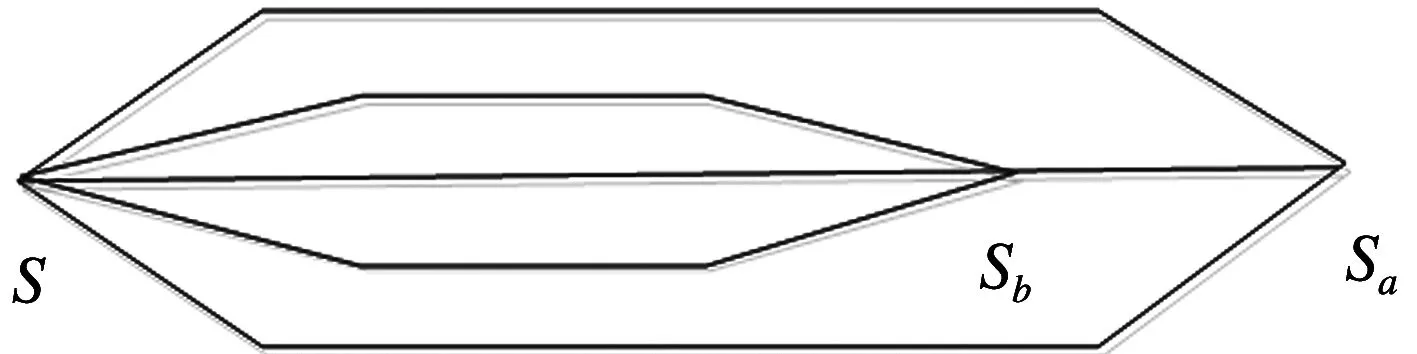
图1 交路图

2 模型的建立

城市轨道交通主要涉及两大主体，乘客和运营企业，因此，大小交路的开行方案也应该以这两方面为主，但由于开行方案的设计还要考虑多方面因素，因此，本文在以列车上座率、运行时间间隔等约束为基础上，从总客流量和平均运距着手，对旅客列车开行方案模型进行求解.

2.1 旅客出行成本

旅客出行成本跟旅客出行时间密不可分，总出行成本是指在一定时间内，旅客总数量乘以平均出行时间.旅客出行时间主要由乘车时间和候车时间决定.

候车时间是指乘客到达车站开始，直至发车为止的等待时间.城市轨道交通候车时间与发车频率有关.在运营时段Ti内，根据大小交路不同，可以得到以下平均候车时间计算公式：

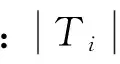
在时段Ti内，大交路区段覆盖的客流为Pa，小交路区段覆盖的客流为Pb，计算方法如下:

Pa=P总f-Pb

式中,fi为全日客流分时段客流比例.

令Ci为时段Ti内大小交路区段上的旅客总出行时间，则

其中：

式中：Tha为a段交路旅客出行时间；Thb为b段交路旅客出行时间；Li为不同交路的平均运距.

最后的总出行成本可以由出行时间乘以出行价值得到.即

其中：C价值为人均出行价值.

2.2 企业运输成本

列车运营成本包括两部分：列车的每列车公里费用Ct和列车的每辆车公里费用Cu.大小交路模式下，开行对数和开行距离都不同，故运营成本为：

式中：Qs为列车车底数，列；为大交路线路长度，km；la为小交路线路长度，km.lb在大小交路模式下，列车所需车底数根据大小交路开行对数不同而有所不同.

2.3 约束条件

2.3.1 旅客列车上座率

在出行时段Ti内，城市轨道交通列车的上座率随着时段不同，区段不同，会呈现出不同的变化.一般情况下，列车上座率都会考虑是否满足高峰时期客流量要求，同时可以在一定范围内浮动.通常，旅客上座率浮动范围为下限γ0(0.7～0.9)，上限γ1(1.2～1.5)，假设高峰时段为(s，s+1)，对应高峰客流量为Gmax(i，j)，则旅客列车上座率应满足：

2.3.2 列车开行频率

列车开行频率随客流变化而变化，但是过于频繁则会影响车辆的使用，所以，在满足客流需求的同时，列车频率要尽可能保持稳定，保证开行数量尽可能少，开行频率要考虑到线路本身能力和市场竞争力，即要满足符合要求的行车间隔，即：

其中,τ为线路最小行车间隔.

3 模型求解

从旅客出行成本最小和运营成本最小两方面出发，综合考虑两者之间的关系，建立了一个双目标的非线性混合整数规划模型.本文参考多篇文献，发现大多数开行方案模型主要变量都为列车编组数量、交路开行数等，对于城市轨道交通，编组数量会根据实际情况进行确定，那么在模型求解上存在的实际变量就变成了大小交路开行对数.故本模型可以简化为以下形式：

当小交路列车数量以大交路列车数量m倍求解后，得到的列车数量可能不符合实际客流情况，非高峰期客流量相对较少时，考虑到经济合理性和运营成本，适当对非高峰期开行数量进行调整.对开行数量相差不大的时段尽可能合并，即

在可行条件下，尽可能保证邻近时段μ的数值最小，以此标准进行合并.

4 实例分析

以大连市快轨3号线为例进行说明.大连市快轨3号线起自大连火车站站，终至金石滩旅游度假区，全长49.15km，小交路线路长度为30.43km，沿线设车站12座.主线为大小交路套跑模式，折返站为保税区站.快轨3号线选用B型车，带司机室载客标准为183 人，不带司机室载客标准为217 人.2020年快轨3号线采用5辆编组，每列车标准载客为983 人.平均速度50km/h，列车的每列车公里费用Ct=50 元/列·km，列车的每辆车公里费用Cu=10 元/列·km，平均运距L1=17.19km，L2=15.54km.根据资料，大连市平均工资水平为4 175元，从而得到人均出行价值C价值=17.39 元/h.2020年预测总客流OD量如表1，分时段客流比例如表2.

表1 快轨3号线2020年预测客流OD表 人

表2 分时段客流比例 %

快轨3号线2020年预测大交路客流量保税区站以后客流量为8 588 人，以此为基础，计算大交路所需开行数量.快轨3号线最小行车间隔为2.5 min，故单位小时内可开行对数应不超过24对，因此，m=3,4,5,6,7.利用枚举法，计算当m值不同时，对应的不同开行方案.

以客流量为基础，计算时间成本与运营成本，并根据约束条件，合并邻近开行数，得到最终列车开行数方案表，如表3.

从表格中可以看出，当m值越大时，出行成本越小，运营成本越大，故计算小交路高峰时期上座率，确定最终m取值，如表4.

表3 列车开行数表 万元

表4 小交路高峰小时上座率对照表 人

m=3m=4m=5m=6m=7上座率1.51769422118265413096535388上座率0.7825710322123861445016514小交路高峰预测客流量2368925269263222707427638

为满足列车上座率要求，且满足出行成本和运营成本要求，最终确定m取值为5.最终列车方案如下图2.

图2 2020年大连市快轨3号线开行方案

应用此模型进行实例验证.结果表明，按照客流出行时段，需要开行列车144列，其中高峰时段开行66列，如图2所示，符合列车上座率要求，同时考虑到了乘客出行成本和企业运输成本，开行方案与实际情况可以较好地吻合.

5 结论

交路的设置会影响客流，也会影响企业运营，所以要进行合理优化，兼顾两者的利益，这就需要考虑多方面因素.本文建立了双约束的大小交路模式下混合非线性整数模型，将大小交路以分担率形式确定客流比例，同时将开行倍数纳入列车开行方案，引入平均运距进行计算，以此来实现大小交路模式下列车数量、开行时段以及大小交路开行倍数的综合优化.

本文研究的假设是大小交路均匀分配客流量，且小交路开行数是大交路的整数倍，研究对象比较固定，对于客流量大或者客流分布不均的交路研究尚浅，这是下一步研究的重点.

[1]王媛媛,倪少权.城市轨道交通大小交路模式列车开行方案的优化[J].铁道学报,2013,35(7):1-8.

[2]牛惠民,陈明明,张明辉.城市轨道交通列车开行方案的优化理论及方法[J].中国铁道科学,2011,32(4):128-133.

[3]邓连波,曾强,高伟,等.城市轨道交通列车开行方案优化方法[J].中国科技论文在线,2010 ,5(10):767-772.

[4]严波.城市轨道交通运营组织优化研究[D].南京：东南大学,2006.

[5]陈胜波,何世伟,何必胜.客流波动条件下城市轨道交通列车开行方案研究[J].城市轨道交通研究,2013(10):53-58.

[6]刘扬.城市轨道交通列车开行方案设计研究[D].西安：长安大学,2015.

Research on Train Operation Scheme of Urban Rail Transit

MA Caiwen, SHI Jing, XU Yanqiu

(School of Taffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116028, China)

By using the train formation, the minimum time interval, train ridership such as constraint conditions is a non-objective integer programming model established based on travel and operations costs, and an average distance of passenger travel time is introduced. By determining the main operation scheme of Dalian Rapid Rail Line 3 to verify the rationality of the model, the results show that the operation scheme satisfy the constraint conditions of this model, which conforms the requirements of the passenger and business interests of both parties.

urban traffic；train operation scheme；nonlinear integer programming; full-length and short-turn operation mode

1673- 9590(2017)02- 0001- 05

2016- 04- 21

马彩雯(1964-)，女，教授，博士，主要从事铁路运输的研究

A

E- mail:macaiwen@126.com.