优化例题教学提高课堂教学有效性

2017-04-06江苏省苏州市吴中区迎春中学215128沈萍

中学数学研究(广东) 2017年6期

江苏省苏州市吴中区迎春中学(215128) 沈萍

优化例题教学提高课堂教学有效性

江苏省苏州市吴中区迎春中学(215128) 沈萍

数学课堂教学离不开例题教学,例题教学是数学课堂教学的中心环节,直接影响着数学基础知识、基本技能、基本思想和基本活动经验的教学.例题既为学生提供解决数学问题的范例,又能体现数学思想,揭示数学方法,规范思考过程.例题教学的好坏直接决定着数学教学的好坏,因此优化例题教学,可以提高课堂教学的有效性.

一、例题选择要有针对性

(一)针对内容选择例题

课堂上所选的例题必须具有很强的针对性和代表性,针对学生的薄弱环节和容易犯的错误以及教学目标、教学重难点来挑选例题.只有这样才能更好的突出重点,突破难点.

比如,要提高计算能力,让学生在计算中避免各类错误,在例题选择时尤其重要.因此,在上“有理数乘方”这节课时,笔者选择了这样一道例题:

选择辨析类型的例题,主要针对学生在计算过程中经常会出现的错误.首先让学生先观察形式上的区别,其次搞清读法、意义上的区别,最后强调当底数是负数或分数时必须要加括号.这种例题,使学生搞清内在和本质,也大大提高学生的计算正确率和计算速度,从而提高课堂教学的有效性.

(二)针对学情选择例题

对于初中生来说,学生学习数学的能力是有差别的,只有按照学生的实际情况去组织、设置教学活动才可以提升其有效性,因此应针对学情选择例题.教师在准备例题的过程中,一定要善于换位思考,站在学生的角度,从学生的实际水平出发,考虑学生的接受能力,根据学生的个体差异,进行例题设计,开展例题教学.

笔者在上二次函数复习课时,为了通过对二次函数的复习渗透初中非常重要的数学思想方法–数形结合思想,在例题讲解中笔者采用了一道中考题:

例(2012兰州)已知二次函数y=ax2+bx+c(a/=0)的图象如图所示,若|ax2+bx+c|= k(k/=0)有两个不相等的实数根,则k的取值范围___.

图1

本题考察了二次函数的图像和性质,以及二次函数与一元二次方程的关系,并渗透了初中阶段十分重要的数学思想方法–数形结合思想,但是有一定的难度.考虑到学生的个体差异性以及学生的实际水平,为了更容易突破难点,笔者将此中考题做了调整,设计阶梯式的问题,将难度分解,更容易达到学生的最近发展区.调整后的题目如下:

1.已知二次函数y=ax2+

bx+c(a/=0)的图象如图2所示,则

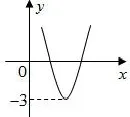
图2

(1)关于x的方程ax2+bx+ c=0根的情况____;

(2)关于x的方程ax2+bx+ c=2根的情况____;

(3)关于x的方程ax2+bx+c=−3根的情况___;

(4)关于x的方程ax2+bx+c=−4根的情况___.

2.已知二次函数y=ax2+ bx+c(a/=0)的图象如图3所示,则

(1)若关于x的方程ax2+ bx+c=k有两个不相等的实数根,则k的取值范围为___;

图3

(2)若关于x的方程|ax2+bx+c|=k(k/=0)有两个不相等的实数根,则k的取值范围____.

将此中考题调整,设置阶梯式的题目,层层递进,一方面使学生对“二次函数与一元二次方程关系”理解透彻,达到一个新的高度;另一方面可使不同层次的学生有不同的发展.

最适合学生的教学就是能让每一位学生在学习中获得相应的知识和成功的喜悦.因此,与学情同步的例题才是最合理、最有效的例题.在例题设计上,要根据学生的实际情况,对学生提出最低要求、一般要求和较高要求,根据学生基础设置不同层次的例题,把原本统一的教学内容变得具有层次性.因此例题教学的有效性会使学生获得良好的学习效果,从而有利于提高课堂教学的质量.

二、例题设计要有整体性

数学具有系统性、逻辑性,各部分知识既密切相关,又相互制约、影响.因此,例题设计时,应注意知识间的联系,考虑知识的整体性,纵向串联新旧知识,形成知识网络.选用的例题应既能复习巩固之前所学内容又能针对本节课的重点,又能为以后的新知埋下伏笔、做好铺垫.只有这样才能完善学生知识结构,提高学生综合解题能力,达到事半功倍的效果.

笔者在上“§1.3探索三角形全等的条件–SSS”时,选用了这样一道例题:

例已知:如图4,AB=AC, DB=DC,点E在AD上,求证: EB=EC.学生根据已知条件“AB=AC,DB=DC,公共边AD=AD”,很容易想到利用“SSS”证得△ABD～=△ACD,从而得到∠BAD=∠CAD;再根据“AB=AC,∠BAD=∠CAD,AD=AD”,利用“SAS”证得△ABE～=△ACE,从而得到BE=EC.

图4

此题在巩固了本节课的新知“判定三角形全等的方法–SSS”的同时,也复习了之前学过的“判定三角形全等的方法–SAS”,用新知巩固旧知,通过聚合新旧知识提高学习效率.同时,也给学生留个悬念:“以后学习了第二章轴对称图形后,会有新的、更简单的证明方法”,以此来激发学生的求知欲,调动学生的学习积极性.

在上“§2.4线段、角的轴对称性”时,此例题笔者再次呈现.在回顾旧法的同时利用新知–线段垂直平分线的性质和判定解决此题,并发现利用线段垂直平分线的性质和判定更简单(如图5).

图5

证明:连接BC∵AB=AC,DB=DC.∴点A、D在线段BC的垂直平分线上.∴AD是线段BC的垂直平分线.∵点E在线段BC的垂直平分线上.∴BE=EC.

因此,例题设计时建立知识的整体性,一方面可以促进学生知识的融会贯通,加强对知识的理解;另一方面学生用自己所学知识探究和发现知识之间的联系,使得学生创新意识得到不断提升.

三、例题讲解要有技巧性

(一)一题多解,拓宽思维

一题多解就是引导学生从不同角度进行思考,运用不同的知识点和方法解决同一问题.既能充分调动学生思维的积极性,调节课堂气氛;又能开拓学生思路、发散学生思维,让学生学会多角度分析和解决问题,培养和发挥学生的创造性.

在上平行四边形习题课时,为了从不同角度、用不同知识解决同一题,笔者选用了这样一道例题:

已知:如图6,在正方形ABCD中,点E、F分别在BD上,且BF= DE.求证:四边形AECF是菱形.

学生在解决此问题时,用的最多的是通过证明三角形全等,来得到证明菱形的条件.如下面解法一、二,

图6

解法一:证明△ABF～=△CBF～=△CDE～=△ADE得到AF=FC=CE=AE,从而证得四边形AECF是菱形.

解法二:通过证明△ABE～=△CDF得到FC=AE,∠AEB=∠CFD;由∠AEB=∠CFD得AE//CF;由FC=AE,AE//CF得平行四边形AFCE;由△ABE～=△EBC得AE=CE;由平行四边形AFCE,AE=CE可得四边形AECF是菱形.

趁学生学习热情高涨时,引导学生从不同的角度思考不同的解法,并适时点拨:不用全等,观察正方形ABCD与四边形AFCE的关系.顿时有学生发现正方形ABCD与四边形AFCE的两条对角线均在一直线,正方形ABCD对角线互相垂直即四边形AFCE的对角线也互相垂直,从而得到解法三如下(图7):

图7

解法三:连接AC,与BD交于O点∵四边形ABCD是正方形.∴AO=CO,BO=DO,AC⊥BD.∵BF=DE,∴FO=EO.∴四边形AFCE是平行四边形.又∵AC⊥BD,∴四边形AECF是菱形.

此例题有三种解法,均用到正方形的相关性质,分别运用了菱形三种不同的判定方法.解法一、二涉及到三角形全等,解法二、三运用不同的平行四边形判定方法.三种解法运用了不同的知识点、从不同角度解决同一道题,既引导学生灵活地掌握知识的纵横联系,提高学生学习热情;又能拓展学生思维,锻炼学生思维的灵活性,从而提高课堂效率.

(二)一题优解,优化思维

在例题教学过程中,从一题多解到一题优解,通过选择最优的解题方法,最简捷地解决数学问题,可以优化学生思维,而这种优化是解题技巧的升华.一题优解可以激发学生去发现和去创造的强烈欲望,加深学生对所学知识的深刻理解,可以培养学生的思维品质,发展学生的创新性思维,培养学生的能力.

笔者在上一元一次方程应用题时,选用了这样一道例题:

例修一条东西方向的公路,总长5m,由甲乙两个工程队共同承建,甲由东向西修建,乙由西向东修建,乙工程队比甲工程队早15天开工,修建过程中,甲工程队由于其他工程开工,中途离开15天,已知甲工程队平均每月修筑1km,乙工程队平均每月修筑0.5km,问甲乙两工程队个修筑多少千米?(每月按30天算)

分析:由“乙工程队比甲工程队早15天开工,修建过程中,甲工程队由于其他工程开工,中途离开15天”知,乙比甲多修30天.这时题目中就出现两个数量关系:①甲修筑的公路长+乙修筑的公路长=5;②乙修公路的时间=甲修公路的时间+30天.

由问题“甲乙两工程队个修筑多少千米?”,所以有个别学生采用了直接设法,等量关系:乙修公路的时间=甲修公路的时间+30天.

解法一较为难列,大多数学生列不出,故引导学生分析“已知甲工程队平均每月修筑1km,乙工程队平均每月修筑0.5km”,由此可知甲乙修的公路长与时间相关,所以可采用间接设法,等量关系:甲修筑的公路长+乙修筑的公路长=5.学生思考后得解法二、解法三.

答:甲工程队修了3千米,则乙工程队修了2千米.

解法三:解设甲修了x月,则乙修了(x+1)月,由题意得x+0.5(x+1)=5 x=3甲修筑的公路长=3×1=3千米,乙修筑的公路长=5−3=2千米答:甲工程队修了3千米,则乙工程队修了2千米.

通过三种方法比较发现,解法三用间接设法设以月为单位的修筑时间最简便,不仅易懂而且方程形式简单易算.因此在一题优解教学中应以学生易通易懂为前提,善于从学生的思路入手比较各种解法的优劣差异,通过提示点拨介绍灵巧的方法,从而训练了学生的最优解题意识.同时引导学生形成开放性思维,锻炼学生思维的广阔性、灵活性和创新性,为以后分析题目,寻找最优方法打下基础.

(三)一题多变,借题发挥

单一的例题类型对于学生来说要完整的掌握和理解知识是不够的,所以教师应选择合适的变式来巩固和提升.将变式教学应用到初中数学教学中,通过改变题目的条件和结论等,将题目“改头换面”,让学生产生好奇心,积极主动地寻找变化题目的联系,在潜移默化中不仅提高了学生的学习热情,训练了思维,而且还提高了学生分析问题和解决问题的能力.

在上“等腰三角形轴对称性”时,为了巩固和灵活运用等腰三角形的性质,选选用了这样一道例题:

例:如图8,在△ABC中,∠ABC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,求∠DAE的度数.

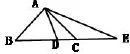
图8

变式一:如图8,在△ABC中,∠ABC=90°,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,求∠DAE的度数会改变吗?

变式二:如图8,在△ABC中,∠ABC＞90°, AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,那么∠DAE与∠BAC有怎样的数量关系?

例题讲解后,改变条件,进行了变式训练.变式一在其他条件不变的前提下,把“AB=AC”的条件舍去;变式二在其他条件不变的前提下,把“∠ABC=90°”变成“∠ABC＞90°”,探究∠DAE与∠BAC有怎样的数量关系.通过这样的变式训练,可以巧妙的变换质疑情境或改变思考角度,从而提升学生的适应能力;可以使学生产生探究欲望,调动学生积极性,可以使学生多角度、多方位对例题思考,从而达到训练思维,培养能力的目的.