以简驭难——一道经典例题的深度研读

上海市向明中学(200020) 侯宝坤

以简驭难
——一道经典例题的深度研读

上海市向明中学(200020) 侯宝坤

课本例题大多是经过编写者精心选择的,有些例题甚至经过几代人磨砺,被多套教材采用的,是有很大教学价值的问题.放弃对教材例题的引用和挖掘,犹如入宝山而空回.使用教材例题、研究教材例题教学价值应成为教师的自觉行动,同时也应把对教材的阅读与研究习惯传输给学生,培养学生的阅读习惯,提升自主学习、自我反思的能力.下面就以一道简单的课本例题来谈谈怎样根据不同学段要求,较为充分的研读例题,挖掘其所蕴藏知识、方法、思想上教学价值.

例题写出{1,2,3}的所有子集和真子集.

这道例题在人教版的历代教材中都有,现在的北师大版、苏教版、沪教版、湘教版也都引用了这道例题,应该是一道经典的例题.

一、例题本体的深度研读

1.例题的一般化处理

一般化是促进数学抽象的需要,是对结论价值、方法应用的深刻理解.一个数学问题的一般化包括问题呈现形式的一般化、结论一般化和方法一般化.

呈现形式一般化,可以将具体的数字变成抽象的字母,并将元素的个数一般化,形成

问题1 写出{a1,a2,···,an}的所有子集和真子集.

结论一般化,就是对一般化的问题形成的结论,对引例而言就是问题1的结论：有n个元素的集合子集共有2n个,真子集共有2n-1个.这个结论可以让高一学生通过列举用不完全归纳法得到,高二、高三则可以作为数学归纳法的一个例子使用.

方法一般化,就是解决问题的方法是否有一般性,是否有更广阔的应用价值,这往往是例题最值得研究的地方.

引例按元素个数和顺序找子集的列举法,是完全可以用到n元集合上,在高一学生的思维最近发展区,学生完全可以列举发现：∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}{d},{a,d},{b,d},{c,d},{a,b,d},{a,c,d},{b,c,d},{a,b,c,d}

体悟出每增加一个元素,子集个数增加一倍,新增加的子集就是原来子集再添上新元素形成的,即子集个数满足递推关系an=2an-1.这个方法告诉学生,要学会从问题产生的顺序上摸清解题思路,要关注前后联系,特别是新对象对问题的影响,形成主动联系的学习习惯.

子集个数问题也是一个装球入盒问题,是典型的计数问题.从形成子集的元素个数分类入手有2n;从某个指定的元素“取”与“不取”两种状态入手,用乘法原理有将问题换个背景,进行跨界处理,也是处理数学问题的灵活手段,是数学知识统一性的体现,对培养学生普遍联系的观点、拓宽知识面是非常有益的;善于从不同角度研究一个知识也是对知识深刻理解的表现,是学习能力提高的表现.

2.对例题不足的补充

认知差异使学生对相关概念、方法理解的程度也会不同,有些问题例题中可能没有涉及,有些可能需要再做些强化,才能使学生有更深透的理解.

对于引例,如想突出和前一节集合的联系,考查集合的互异性,也可以在引例前设计：

问题2{a,2}⊆{0,1,2},则a=___.

如觉得引例中∅会遗忘,经过点明学生会补充,但不一定真理解到∅的意义,可以设计：

问题3{x|ax=0}⊂{1,2},求a的取值.

有人认为上面都是离散的数集,对象简单,方法仍是列举没有突破,可以设计：

问题4{x|a≤x≤2a+1}⊆{x|-1≤x≤3},求a的取值范围.

如想突破数集,可以设计：

问题5 非空集合A={(x,y)|y=2x,1≤x≤a},集合B={(x,y)|y=kx,m≤x≤a},若A⊆B,求实数k,m应该满足的条件;

如想突出问题4“取等号”这个细节以及子集与真子集的区别,可以设计：

问题6{x|a≤x＜2a+1}⊆{x|-1≤x≤3},求a的取值范围;

问题7{x|a≤x＜2a+1}⊆{x|-1≤x＜3},求a的取值范围;

问题8{x|a≤x＜2a+1}{x|-1≤x≤3},求a的取值范围.

上午9时整，升旗仪式正式开始。随着铿锵有力的号令声，3名升旗手手擎一面国旗、两面厂旗，在10名护旗手的护卫和干部职工的注目礼下，迈着坚定有力的步伐走向升旗台。伴随着雄壮的《中华人民共和国国歌》和催人奋进的《开磷之歌》，国旗与厂旗在庄严注目下冉冉升起。砥砺拼搏六十载，开磷披荆斩棘仍旧斗志不减；风雨兼程六十载，开磷历经沧桑依然奋发昂扬；峥嵘岁月六十载，开磷牢记使命镌刻时代丰碑；春华秋实六十载，开磷扬帆筑梦谱写辉煌华章。

将一个简单例题演化为相对复杂的同类问题,根据课堂需求组成问题串,就可以非常到位地帮助初学者建立和理解相关概念,知晓易错点,初步体会数学问题产生的途径,逐步养成关注细节、大胆列举、反思探究的良好习惯.

二、前后知识的关联性研读

对例题的研读不能仅停留在本节课的理解和设计上,更应当从问题的关联性入手,加强知识的前后联系,使例题的价值得到更大发挥.一般可以从知识点的关联性和思想方法的关联性两个方面去挖掘加深.

1.知识点的关联性

子集与求交、并、补集的运算联系较明显了,有A∩B⊆A(B)⊆A∪B,A∩B=A⇐⇒A⊆B⇐⇒A∪B=B,B∪CUA=U⇐⇒A⊆B⇐⇒A∩CUB=∅,A∩B=∅⇐⇒A⊆CUB等.在单元复习时,将子集与交、并、补运算结合,可设计综合问题：

问题9 非空集合A,满足A⊆{1,2,3,4,5,6},若x∈A,则必有2x∈A,求所有满足条件的集合A.

问题10 已知集合A⊆{1,2,3,4,5,6,7},且A∩{1,2,3,4}={1,2},求所有满足条件的集合A有多少个?

子集也是集合,所以它的落脚点必然是元素,必然要考虑集合所具备的性质,集合元素的“取”可能更难些,子集的“取”只是元素个数的问题了,其实集合的交、并、补运算也是怎么“取”元素的问题,所以说“怎么取”才是集合的核心问题,这也是集合与排列组合的联系所在.基于这种知识的关联性理解,我们可以设计加深子集的理解问题：

问题11 已知集合A={1,2,3,4,5,6,7},含有元素1的子集有多少个?含有元素6的子集有多少个?所有子集的元素之和是多少?如果A={1,2,···,n}上述问题答案如何?

问题12 将集合A={a1,a2,···,ak},且a1＜a2＜···＜ak,我们称a1-a2+a3-a4+···+(-1)k-1ak为集合A的交错和,求{1,2,···,n}所有子集的交错和的和.

问题12与问题11思路相同,每个元素出现的次数刚好是剩下的元素所形成的子集个数,为2n-1,和为2n-1(1+2+···+n)=2n-2n(n+1),这个问题高一单元复习可以使用.问题12对于元素1它始终为正,元素i(2≤i≤n)前的“+,-”由它在子集中的位置决定,当从1,2,···,i-1取偶数个数在子集中时i为“+”,所以“+”出现次,同样“-”也出现刚好相互抵消,所以答案为2n-1.这道题考虑元素出现的方法与上面是一样的,只是用了简单的组合性质,可以作为高三的复习用题,或者改成较小数字,成为高一的拓展用题.

2.思想方法的关联性

一个例题最重要的价值是,它所蕴藏的思想方法是不是有进一步拓广的价值.能帮助我们解决相似相关的问题的价值就高,过于关注技巧而没有一般性的价值就低.引例所涉及的列举法、从特殊到一般、代表元素法、递推思想都具有一般性,对其他类似问题具有指导意义,以下举例的难度稍大,可以作为高年级的课外活动.

列举法是解决集合、数列、计数等复杂问题的有力手段,也是从特殊到一般思想方法的具体体现.通过列举可以发现结论的规律性,更为重要的是在列举的过程中发现形成这一规律的原因,从而找到解决问题的办法;列举是典型的从特殊到一般的思维方式,从简单具体的事例出发,发现并抽象从一般性的规律,是解决复杂问题的有效手段.譬如下面问题：

问题13 已知集合A={a1,a2,···,an},B={x|x=ai+aj,i/=j,i,j=1,2,···,n},n≥2,求B集合元素个数的最大、最小值.

解析要使元素少,那么ai+aj出现重复的数值就要多;要多,重复就少.给我们的问题比较抽象,我们先将问题特殊为An={1,2,···,n}(再慢些用{1},{1,2},{1,2,3}等)来体会,此时Bn={3,4,···,2n-1}共2n-3个元素;如果将最大数换成n+1,即An={1,2,···,n-1,n+1},此时Bn={3,4,···,2n}增加一个元素,为2n-2;如果将最大数换成n+2,即An={1,2,···,n-1,n+2},此时Bn={3,4,···,2n+1}又增加一个元素,为2n-1;……,当最大数换成2n-3,时Bn={3,4,···,3n-4}元素个数为3n-6;最大数再变大时B中元素个数不再增加.我们发现：

(1)对An={1,2,···,n}最大元素变化时,集合元素个数从最小2n-3连续取到最大.

(2)当最大数字变大时,新集合中数字与原来由An-1={1,2,···,n-1}形成的Bn-1集合重复元素减少,当An最大值大于Bn-1的最大值后就不再有重复数字,这时所有这样的Bn比Bn-1都多n-1个元素.

所以要想元素最多,所取的数必须不小于前面两个最大数的和,如取著名的斐波那契数列{1,2,3,5,8,13,···}和等比数列{1,2,4,···,2n-1}构成的集合,它们元素最多,为最少为2n-3.

抽象的也可以简单证明,元素最多就是所取任意两数和都不相等,为如我们所构造的两个例子,构造法证明存在性就是一般转化为特殊.下面证明最小：

不妨设a1＜a2＜···＜an,显然,a1+a2＜a1+a3＜a1+a4＜···＜a1+an＜a2+an＜a3+an＜a4+an＜···＜an-1+an共有2n-3个,如我们构造的An={1,2,···,n}.

如果再更一般的追问：B={x|x=ai+aj,i/=j,i,j= 1,2,···,n}的元素个数能否取遍2n-3到中的所有整数?

这时,上面列举的价值就可以得到充分体现了,利用数学归纳法,我们只证明第二步：

假设n=k时,集合B元素个数取遍2k-3到中的所有整数.

当n=k+1时,由发现(2),此时B元素个数取遍(2k-3)+k到中的所有整数,即取遍3k-3到中的所有整数;由发现(1)知,当n=k+1时,B元素个数取遍2(k+1)-3到3(k+1)-6=3k-3中的所有整数;综合即知结论成立.

集合是由一类具有共同性质的元素构成的,代表元素法就是选取集合的一个元素作为研究的对象,集中力量研究它的构成和性质,是一种以点带面的解题方法,是解决抽象集合问题的有效手段.譬如：

问题14 取集合{1,2,3,···,n}的所有含有m个元素的子集,再将子集中的元素从小到大排列,则所有子集的第r个元素的平均数为多少?

解析本题关键在求第r个元素的和,第r个元素前有r-1个元素后有m-r个元素,将第r个元素分类为：r,r+1,···,k,···,n-(m-r),选取代表元素k研究：k前面元素有取法,后面元素有种取法,所以第r个元素是k的集合共有根据分析,如果按照第r个元素的不同将这些子集分类,根据加法原理我们有：

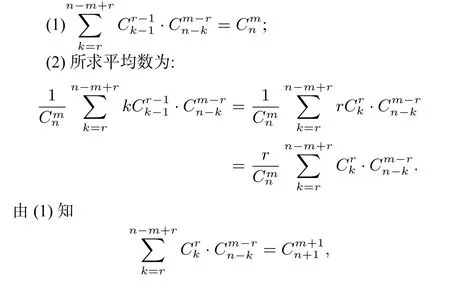
值得注意的是,解题过程中要注意分析结论以外的东西,加强对问题条件的理解和应用,尽量产生更多有用有趣的结论,使问题能向纵深发展.

问题1的解决表明,数学规律的发展通常是有先后顺序的,是相互关联的.如果能厘清先后关系,找出它们的数量关系或者变化特征就能使问题得到解决.前后关系中表现最为典型的就是递推关系和数学归纳法,它们也是解决与整数有关问题的有力手段.比如：

问题15 证明：方程x2-2y2=1有无穷多组正整数解.

解析要证明有无穷多组正整数解,不可能穷举,只能构造解的递推关系,来完成解是可以不断产生的.首先猜出一组解然后建立递推关系式

根据上述推算,由此产生的解是递增的正整数,且有无数个.

通过对例题本体性研究,可以促进我们对例题所包含的知识有更为深透的理解;通过一般化研究,可以验证涉及的方法是否具有更广阔的前景,同时也加深了对方法的体会,为灵活使用奠定基础;通过对不足的自觉反思,加强变式研究,促进了对知识的全面升华.

知识关联性研究,可以使知识前后连贯,相互关联,气势相通,形成四通八达的网络结构,使知识更加牢固灵活;同时也可以培养善于联想的思维品质.数学思想方法的关联则更为深刻,通过对思想方法的领悟,可以由点及面、由例及类的解决一大片问题,甚至解决与原例相去甚远乃至面目全非的问题,通过思想方法的关联可以培养更有深度和跨度的思考能力,使思维更加通透深刻.