渗透转化思想

汪艳丽

“转化”是研究和解决数学问题的一种有效方法，它通常采用将未知问题转化为已知问题、将抽象问题转化为具体问题的方式，降低教学难度，破解教学难点。笔者以“人教版”《数学》课标实验教材五年级上册第五单元《平行四边形的面积》教学为例，谈谈转化思想在教学中的具体运用。

一、在课前导入中渗透转化思想

导入在一节课中所占的时间比例不大，但它对于明确学习任务和目标、激发学生的学习兴趣和求知欲等具有重要的作用。

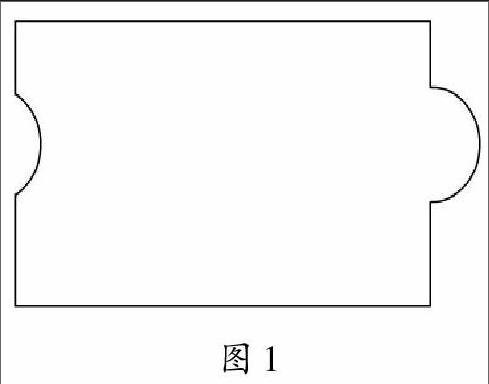
教学时，笔者采用了课前游戏——“小小魔术师”的方式导入。教师问学生喜不喜欢魔术表演，并故作神秘地说：“今天老师带来了一个道具让你们变魔术。”学生的兴趣被调动起来了。教师出示一个不规则的图形（图1），问：“你们能计算出这个图形的面积吗？”学生一脸茫然，不知道该怎样计算。

“如果是一个长方形，你们能计算出它的面积吗？”教师追问，“小小魔术师，你们会将这个不规则的图形变成长方形吗？”学生通过观察，发现把右边的半圆剪下来，向左平移到缺口处，就能拼成一个长方形。教师根据学生的讲述，把右边凸出的部分剪下来，补在了左边凹进的地方，让图形构成了一个规则的长方形，并告诉学生，这种方法叫割补法。教师还进一步告诉学生：这个不规则的图形经过割补，变成了一个规则的、可以直接计算出面积的长方形。这种把未知转化成已知再求解的思想，就是转化思想。

简短的导入，不仅营造出活泼、快乐的学习氛围，而且让学生初步感知了转化思想，为后面的学习打下了基础。

二、在自主探究中渗透转化思想

1.创设情境，提出问题

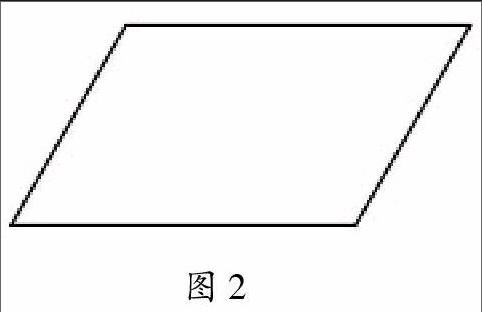
导入后，教师进一步用动画激发学生兴趣。教师一边播放懒羊羊和美羊羊到蛋糕店应聘的视频，一边旁白：“同学们，咱们的好朋友懒羊羊和美羊羊今天到村长开的蛋糕店里去应聘，可是村长给他俩出了一道难题——谁能算出下列图形的面积（图2），谁就应聘成功。你愿意帮助他们吗？”

助人为乐是孩子们愿意做的事情，何况现在帮助的还是他们最喜爱的懒羊羊和美羊羊呢！学生的求知欲被充分调动起来。问题也随之出现了：以前只学习过长方形面积的计算方法，而没学过平行四边形面积的计算方法，怎么帮呢？教师抓住学生的疑惑，顺势板书课题——平行四边形的面积。

2.放飞思维，大胆猜想

“怎么帮呢？”教师引而不发，让学生自己想办法解决这个问题。个别机灵的学生发现了教师课前发给大家的学具——画有方格的长方形和平行四边形格子纸、印有平行四边形和长方形的纸、长方形纸片、平行四边形纸片、剪刀等，并提出“可以用数格子的方法求出面积”的想法。教师肯定了学生的想法，并让他们试着数一数。长方形的面积很容易就数出来了——长方形的长由6个小方格组成，即6厘米；宽由3个小方格组成，即3厘米；整个图形共有18个小方格组成，即总面积是18平方厘米。数平行四边形的面积时，学生遇到了困难——图中有很多半格的格子，且大小不等，该怎样计算面积呢？教师让大家联系开课时的内容想一想。学生通过观察，恍然大悟——每个半格都能找到一个对应的半格，用割补法把它们组合起来，可以构成一个完整的小方格，即1平方厘米；这就是说，每两个半格就是一个方格。按照这样的思想，学生很快算出了这个平行四边形的面积也是18平方厘米。

用数方格的方法计算平面图形的面积固然直观，但局限性很大，不利于操作，有没有更好的方法呢？因为有前面几个步骤作铺垫，学生很快想到，能不能把平行四边形转化成我们学过的图形呢？

3.自主探讨，验证猜想

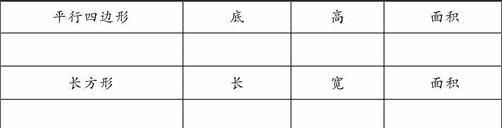
一个理性、正確的思想胜过十个随性、自由的行动。学生能自主地提出这种想法，说明教学已成功了一半。教师让学生利用课桌上的学具以及“割补法”，小组合作研究这个问题，并在研究的过程中填写下列表格。

学生迫不及待地动起手来。通过割补，他们发现：沿着平行四边形的高剪下图形的一部分，然后把这一部分平移到图形的另一边，补充图形空缺的地方，平行四边形就转化成了长方形；这个长方形的长等于原平行四边形的底，宽等于原平行四边形的高，面积与原平行四边形的面积相等。

至此，平行四边形面积的计算方法呼之欲出：因为长方形的面积=长×宽，所以平行四边形的面积=底×高。教师进一步告诉学生：在数学中，我们经常用字母表示公式，使公式变得简单好记。如果用S表示平行四边形的面积，用a表示平行四边形的底，用h表示平行四边形的高，那么平行四边形的面积公式就可以表示为S=a×h，或S=ah。

三、在巩固练习中渗透转化思想

数学源于生活，寓于生活，服务于生活。为了让学生感受数学与生活的联系，培养学生的数学应用意识，教师本着“重基础、验能力、拓思维”的原则，设计了四个层次的练习题——基础练习题、提高练习题、拓展练习题、开放练习题。

基础练习部分，教师出示了几个平行四边形，让学生先用尺子量出图形的底和高，然后直接用公式求出图形的面积。

提高练习部分，教师设计了两道题：一、出示图3，让学生求出图形的面积。图3已知两条高和一条底，哪些才是需要的条件呢？这道题的目的就是通过多余条件，引起学生思维的混淆，让他们在质疑、解答中明白，只有底和高相对应，才能准确地求出平行四边形的面积。二、出示图4，要求学生求出图形的高。这是一道变式题，目的是引导学生通过变换面积公式，推导出平行四边形高的计算公式，即h=[sa]。

拓展练习部分，教师出示了两个等底等高的平行四边形（图5），要求学生判断它们的面积是相等还是不相等，或是无法判断，目的是让学生理解等底等高的平行四边形面积相等。

开放练习部分，教师引入了“阿凡提的故事”。教师先用课件播放故事：巴依家有一块用篱笆围成的长方形菜地，他想找人给菜地翻土却又不想给工钱。于是，巴依对阿凡提说：“阿凡提，我和你打个赌——如果你能在今天上午帮我把这块菜地翻一遍土，我就给你一只羊。”阿凡提说：“好啊。”巴依说：“你可不要耍花样！我这块菜地的篱笆长20米，宽10米，你要是把我的篱笆弄短了1厘米，就要赔我一只羊。”阿凡提说：“没问题。”等巴依走后，阿凡提动手把篱笆调整了一下，在没有改变篱笆四条边的长度的情况下，让菜地的面积变小了很多。因此，阿凡很快就翻完了土，牵走了羊。

听完故事后，教师问学生：“你们知道阿凡提是怎么做到的吗？”学生在讨论的基础上，拿出课前准备的长方形框架进行实验。通过实验，他们发现：沿着长方形框架的对角拉，长方形就变成了平行四边形。拉伸后的平行四边形与长方形周长一样，但高比原来短了，所以面积变小了。