由浅入深，逐步培养学生抽象概括能力

陈湘芬

思维能力是人的认识能力（即智力）的核心，而抽象概括能力是其中的重要组成部分。然而，当前教学中经常遇到的情况是：学生对具体、形象、鲜明的内容比较感兴趣，对抽象的内容不易接受。

如何提升学生的抽象概括能力呢？现以北师大版《数学》五年级下册《包装的学问》一课为例，谈谈个人的教学体会。

一、从表象开始，逐步抽象

表象是连接感性认识和理性认识的桥梁。要培养学生的抽象思维能力，教师首先在教学中要引导学生学会逐步抽象，重视表象在形象思维向抽象思维上升过程中的作用。运用观察、操作、实验等多种形式，调动学生多种感官参与感知，指导学生用抽象的方法解决问题。

活动一：包糖果

六一节快到了，教师在准备礼时想把两盒同样大小的糖果包成一包，怎样包才能节约包装纸？（接口处不计，单位：cm）

1.议一议

师：看到这个问题，说说你是怎么想的？

生1：要节约包装纸，就要使两包糖果拼起来的表面积最小。

生2：可以用学具拼一拼，看看哪种包装方法表面积最小。

生3：还可以看看哪种包装方法重叠部分面积最大。

……

2.拼一拼

两盒糖果包成一包，可以怎样包？有几种不同的方案？

同桌合作，动手拼一拼，弄清几种不同的包装方案。

3.算一算

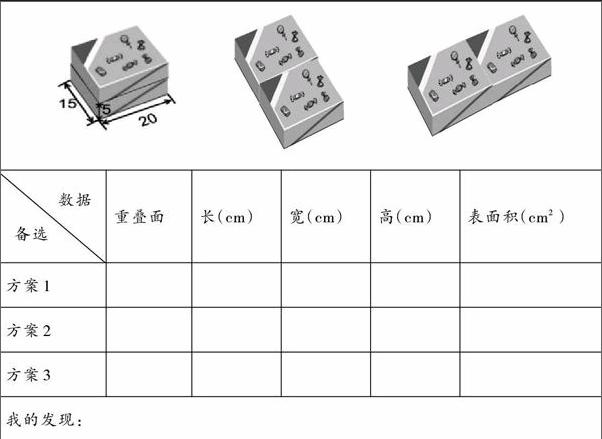
如图，你能计算出哪一种方案最节约包装纸？想一想、填一填。

4.学生独立计算，反馈汇报，交流自己的发现

在这一活动中，学生不难发现，包装两盒糖果，拼成长方体后表面积有3种不同情况，重叠面越大，表面积越小。

简单的包装拼接游戏，让学生通过动手操作找到解决问题的途径。接着，又让学生整理归类完成表格，再观察比较说说自己的发现。这样，就让学生从表象开始，逐步培养抽象概括的能力。

二、重比较类推，建构抽象

数学的完整性和严密性，使得数学结论和方法都具有相关性和相似性。在课堂教学中教师要充分利用这些相关性和相似性，注重类比联想，让学生自己探索和发现许多新的结论或方法，再通过发掘新知识的相同点或相似点进行类比和推理，从而实现知识的迁移和方法的创新，逐步形成抽象思维能力。

活动二：包磁带

1.将四盒磁带（长，110mm；宽，70mm；高，16mm）包成一包，你能想出几种包装方法？可以先画出草图，再在小组内进行交流。

2.说一说自己的想法。

3.小组合作算一算、填一填，哪一种方案最节约包装纸？你有什么发现？

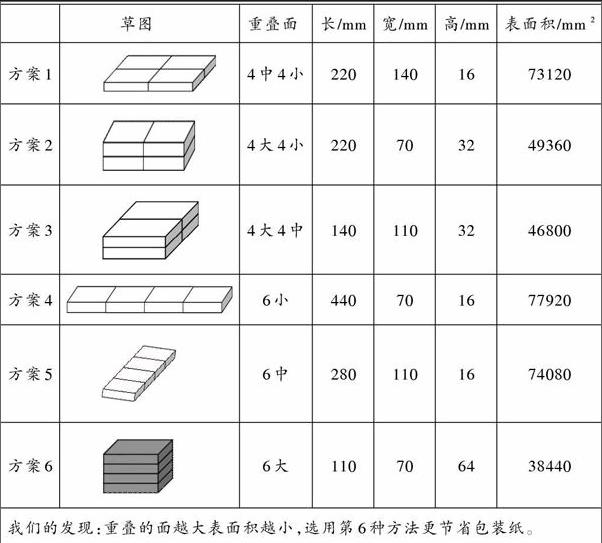
学生分析比较后，反馈汇报：6个大面重叠时，更节省包装纸。如下表：

4.交流体会

对照这些数据和我们的思考过程，你有什么想法？

学生发现：将一盒长方体磁带的长、宽、高分别看成单位1，无论哪种包装，新长方体的总体积一定（长×宽×高=4），而且6种包装法分别是4=2×2×1；4=2×1×2；4=1×2×2；4=4×1×1；4=1×4×1；4=1×1×4。

本活动中，学生发现，包装4盒磁带，表面积出现了6种不同情况，包装多个相同的长方体，方案有多种，把面积最大的面重叠起来，最节约包装纸，也便于携带。每一个方案都让学生切实体验到了知识的获得过程，又在比较归纳中发展了抽象概括能力。

三、重应用检验，深化抽象

“知识不等于能力，能力生发于实践。”数学教学中要实现数学知识的有效迁移、同化，还需要引导学生回到学习中去应用检验。

活动三：包更多物品

如果有更多的长方体磁带盒（出示12盒磁带）进行组合包装，猜猜是不是也像刚才一样，只要大面重叠就最节省包装纸呢？下面动手操作验证猜想。

1.要求：小组合作，拼一拼，拼完后，请组长展示你们组认为最节省包装纸的拼法。

2.反馈讨论：

（1）说一说，你们组有几种不同的拼法？展示你们组认为最节省的拼法？

（2）算一算，算出最节约的拼法减少的面积？

（3）想一想，为什么这样拼最节约？

3.交流体会

每次操作完后，笔者组织学生进行讨论、归纳规律。当磁带盒增加到12个时，有15种拼法。受之前拼4盒磁带盒的影响，学生认为大面重叠最节省包装材料，却忽略了排两排更节约，又便于携带。当长、宽、高三个数最接近时，即它们相加的和最小的时候，表面积最小。最后，学生发现：考虑不同包装方案，可以从“长×宽×高”入手寻找，做到有序思考。

通过比较辨别、应用检验，让学生充分发挥团队精神进行小组合作探究，感受到了思考问题时要注重多角度、有序思考，从而充分培养学生优化思维和求异思维，训练了学生的空间思维，深化了学生的抽象概括能力。

四、重活动延伸，升华抽象

抽象概括过程是认清数学对象的本质，从感性上升到理性的过程，它贯穿于数学学习与教学过程的始终。因此，教师要重视拓展活动，让学生回归生活，在社会实践中类比、归纳、猜想、推理，从而升华他们的抽象概括能力，使他们学会发现并总结数学规律。

活动四：设计新包装

师：今天我们探究了《包装的学问》，你有哪些收获？还有疑问吗？

（引导学生反思学习活动的价值）

师：请你们留心生活，看看超市里哪些商品的组合包装比较特别？想想廠家为什么这样包装？你能为它的包装设计新方案吗？

生活是数学实践和创新的源泉，只有让学生回归生活，在真正的社会实践活动中去感受，才能打破思维定势，促进实践创新。

《包装的学问》从简单的表象开始，让学生逐步接触抽象概括，并夯实了“类比推理”与“应用检验”这两个重点环节，最后还布置了一个创新性的实践活动。这样的教学虽然很费时间，却抓住了“由浅入深培养学生抽象概括能力”这一关键。数学的学习不能仅仅让学生被动吸收教材知识，更要让学生主动参与、亲身实践，充分发展抽象概括能力。