并联系统下屏蔽数据新模型的统计分析
2017-04-05徐晓岭王蓉华顾蓓青
徐晓岭,王蓉华,顾蓓青
(1.上海对外经贸大学统计与信息学院,上海 201620; 2.上海师范大学 数理学院,上海 200234)
【基础理论与应用研究】
并联系统下屏蔽数据新模型的统计分析
徐晓岭1,王蓉华2,顾蓓青1
(1.上海对外经贸大学统计与信息学院,上海 201620; 2.上海师范大学 数理学院,上海 200234)
给出了并联系统下屏蔽数据新模型,修正了原有的基本假定,在此基础上推导了相应的似然函数,在全样本、定时截尾样本场合下研究了参数的极大似然估计,并通过Monte-Carlo模拟算例验证方法的可行性。
并联系统;屏蔽数据;似然函数;极大似然估计
在可靠性分析中,人们往往通过分析系统的寿命数据来估计该系统中各组成单元寿命分布中的未知参数。系统寿命试验数据包括两个方面,一是失效时间,二是失效原因。理想状态下,系统的寿命数据应该包括系统失效的具体时间以及由哪个单元失效导致整个系统失效的信息。但大多数时候,导致系统失效的那个单元并不能够被准确识别出来,人们仅能够把导致系统失效的原因归结为某些单元所组成的一个集合,系统真正失效的原因被屏蔽掉了。在现实生活中,由于故障诊断和故障检测所需的费用昂贵,特别是在现代系统中越来越多地采用模块化设计,引起系统失效的确切单元通常都是未知的。在计算机或集成电路等进行系统可靠性研究时,也会遇到相类似的屏蔽问题。导致屏蔽发生的原因很多,如:经费的不足、时间的限制、记录的错误,诊断工具的缺乏及由某些单元失效所带来的一些破坏性的后果等。这使得屏蔽数据的统计分析成为近年来研究的热点问题之一,许多学者做了很好的工作,并取得了一系列的研究成果,在此不一一列举。值得指出的是国际上屏蔽数据参数的估计问题最早是由Usher和Hodgson于1988年在文献[1]中首次提出来的,在给出几个基本假定基础上研究其统计分析方法,其中最为关键的假定可表述为“屏蔽的发生与失效原因及时间无关(即独立)”,也有学者称为对称性假定。在此以后的众多研究成果无论是串联系统、并联系统还是混联系统都是建立在这一基础之上的。就并联系统屏蔽数据的统计分析而言,国外的文献见[2-6],国内的文献见[7-11]。
本文给出了并联系统下屏蔽数据新模型,修正了原有的基本假定,在此基础上推导了相应的似然函数,在全样本、定时截尾样本场合下研究了参数的极大似然估计,通过Monte-Carlo模拟算例说明方法的可行性。
1 并联系统下屏蔽数据新模型的基本假定
基本假定1:系统由J(≥1)个独立单元并联而成。
基本假定2:将n个同样的系统进行寿命试验,试验持续到时间τ为止,此时共有r个系统失效。(即所谓的定时截尾寿命试验)
基本假定3:屏蔽的发生与失效原因及时间相关,当屏蔽发生时,其对应的失效原因单元(即造成系统失效的单元)被屏蔽的概率(简称屏蔽概率)为该单元在此时的可靠度,而与失效单元集中的其他单元无关。
值得指出的是以前文献中的基本假定3表述为“屏蔽的发生与失效原因及时间无关(即独立)”,其即为通常所言的对称性假定,失效原因是指明确由于具体某个单元失效而导致系统失效。该假定即指所有单元的屏蔽概率相同。但这与实际情况很不一致。因为针对并联通常来说可靠性高的单元其失效概率自然会比较小,被屏蔽的失效原因是可靠性高的单元的概率相对也比较高。在此假定屏蔽概率是该单元此时的可靠度,可靠性越高,失效概率越小,其屏蔽概率也越大。这比较符合实际情况。
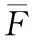
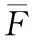
2 并联系统下屏蔽数据新模型的似然函数
考虑n个并联系统进行寿命试验,每一个系统有J个单元。记Tij表示第i个系统的第j个单元的寿命,是一随机变量。其观察值记为tij,i=1,2,…,n,j=1,2,…,J.于是可得到第i个系统的寿命Ti为:Ti=max(Ti1,Ti2,…,TiJ),其观察值记为ti,i=1,2,…,n。记Si为引起系统i失效的单元集合,si为Si的实现。于是,观察的数据data包括(t1,s1),(t2,s2),…,(tn,sn).如果集合si只含有一个元素或由单个元素组成,则表明引起系统i失效的单元是确知的。如果集合si中的元素不只一个,则说明引起系统i失效的单元寿命数据被屏蔽掉了。

就系统i而言,分两种情形,情形一:si中的元素只有一个;情形二:si中的元素不只一个。
情形一:si中的元素只有一个
P(ti≤Ti≤ti+dti,Ki=j)
而P(ti≤Ti≤ti+dti,Ki=j)表示系统i的第j个单元在时刻ti失效,其他J-1个单元(除第j个单元)的寿命小于ti,即
P(ti≤Ti≤ti+dti,Ki=j)=
情形二:si中的元素不只一个,此时,系统i发生了屏蔽。
P(ti≤Ti≤ti+dti,Si=si)=
P(Si=si|ti≤Ti≤ti+dti,Ki=j)
而当j∉si时,
P(Si=si|ti≤Ti≤ti+dti,Ki=j)=0
由此:
P(ti≤Ti≤ti+dti,Si=si)=
P(Si=si|ti≤Ti≤ti+dti,Ki=j)
当j∈si,称P(Si=si|ti≤Ti≤ti+dti,Ki=j)为系统i在失效时刻ti时失效原因单元j被屏蔽的概率,简称屏蔽概率。
注意到,屏蔽概率还可写为:
P(Si=si|ti≤Ti≤ti+dti,Ki=j)=
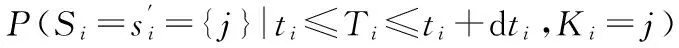
考虑到系统i屏蔽发生,其观察数据为(ti,si),j∈si,于是可以认为有:
P(Si=si|ti≤Ti≤ti+dti,Ki=j)+
而P(ti≤Ti≤ti+dti,Ki=j)表示系统i的第j个单元在时刻ti失效,其他J-1个单元(除第j个单元)的寿命小于ti,即:
P(ti≤Ti≤ti+dti,Ki=j)=
当j∈si且si中的元素不只一个时,即有屏蔽发生的情形下,由假定3′知:当屏蔽发生时,其对应的失效单元的屏蔽概率为该单元在此时的可靠度,而与失效单元集中的其他单元无关。于是有
P(Si=si|ti≤Ti≤ti+dti,Ki=j)=
综上
P(ti≤Ti≤ti+dti,Si=si)=
P(Si=si|ti≤Ti≤ti+dti,Ki=j)=
1) 全样本场合下的似然函数
假设将n个并联系统进行寿命试验,不妨设在观察的数据(t1,s1),(t2,s2),…,(tn,sn)中,前k个系统没有屏蔽发生,即si,i=1,2,…,k中的元素只有一个,而后n-k个系统有屏蔽发生,即si,i=1,2,…,k中的元素不只一个。于是似然函数为
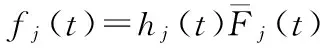
2) 定时截尾场合下的似然函数
如果系统由两个单元并联而成,即J=2。失效的原因可归结为三类:s1={1},s2={2},s12={1,2}。现考虑将n个由两个单元并联而成的系统进行定时截尾寿命试验,试验持续到时间τ为止,此时共有r个系统失效。在这r个失效系统中,属s1类的有r1个,其失效时间不妨设为t1,t2,…,tr1;属s2类的有r2个,其失效时间不妨设为tr1+1,tr1+2,…,tr1+r2;属s12类的有r3个,其失效时间不妨设为tr1+r2+1,tr1+r2+2,…,tr。其中r1+r2+r3=r。于是该n个并联系统在定时截尾寿命试验下的似然函数为

特别地,当系统进行定数截尾寿命试验时,定数截尾数为r,此时似然函数为
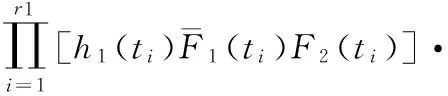
3 并联系统下屏蔽数据新模型的统计分析
1) 全样本场合下的统计分析
如果系统由两个单元并联而成,即J=2。失效的原因可归结为三类:s1={1},s2={2},s12={1,2}。现考虑全部失效时,属s1类的有r1个,其失效时间不妨设为t1,t2,…,tr1;属s2类的有r2个,其失效时间不妨设为tr1+1,tr1+2,…,tr1+r2;属s12类的有r3个,其失效时间不妨设为tr1+r2+1,tr1+r2+2,…,tn。其中r1+r2+r3=n。于是该n个并联系统在寿命试验下的似然函数为

设单元1的寿命为X,其失效率为常数α1,单元2的寿命为Y,其失效率为常数α2,X,Y相互独立,并联系统的寿命记为T,T=max(X,Y)。
似然函数为:
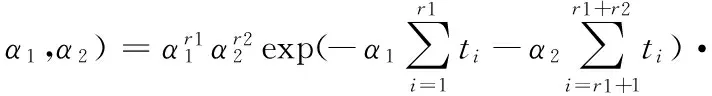

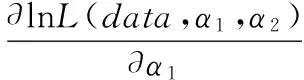
特别地,当两个单元的失效率为相同参数时,即α1=α2=α,此时,似然函数为:
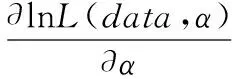
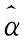
引理1:对ti,i=1,2,…,n,α>0,α的方程g(α)=0有唯一正实根。
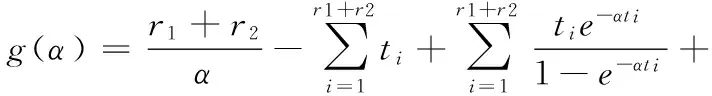
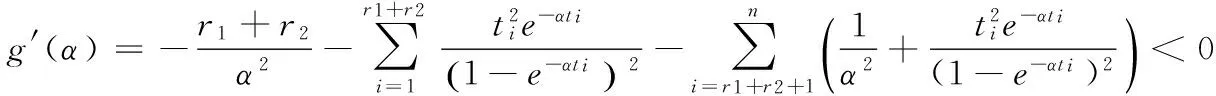
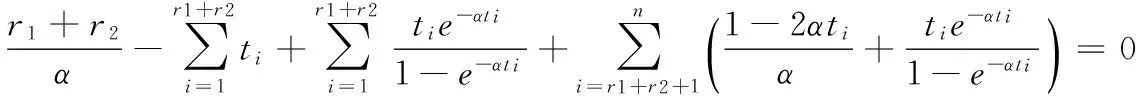
例1:取样本容量n=10,r1=3,r2=4,失效率都取为α=0.5α=0.5,通过Monte Carlo模拟产生如表1所示的随机数。
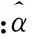
2) 定时截尾下的统计分析
如果系统由两个单元并联而成,即J=2。失效的原因可归结为3类:s1={1},s2={2},s12={1,2}。现考虑将n个由两个单元并联而成的系统进行定时截尾寿命试验,试验持续到时间τ为止,此时共有r个系统失效。在这r个失效系统中,属s1类的有r1个,其失效时间不妨设为t1,t2,…,tr1;属s2类的有r2个,其失效时间不妨设为tr1+1,tr1+2,…,tr1+r2;属s12类的有r3个,其失效时间不妨设为tr1+r2+1,tr1+r2+2,…,tr。其中r1+r2+r3=r。
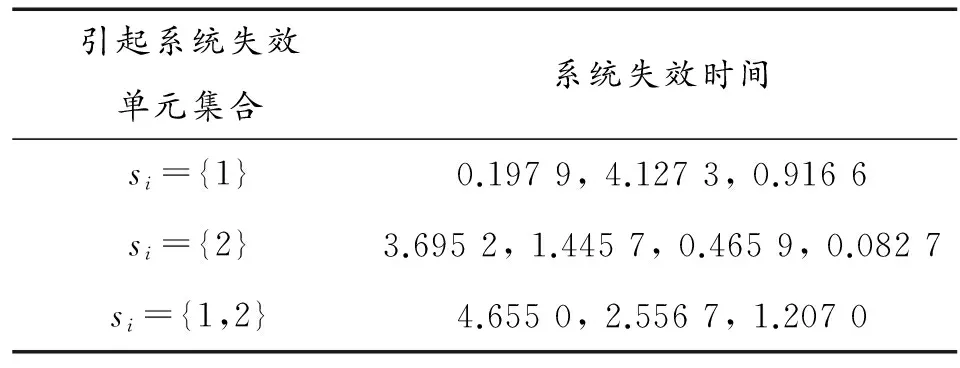
表1 n=10,r1=3,r2=4,α=0.5的随机数
设单元1的寿命为X,其失效率为常数α1,单元2的寿命为Y,其失效率为常数α2,X,Y相互独立,并联系统的寿命记为T,T=max(X,Y)。对t≥0,
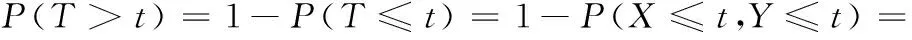
似然函数为:
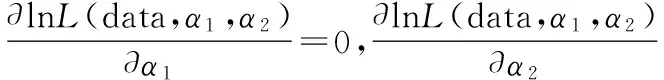
特别地,当两个单元的失效率同为参数时,即α1=α2=α,此时,似然函数为:
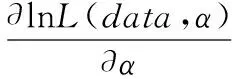
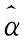

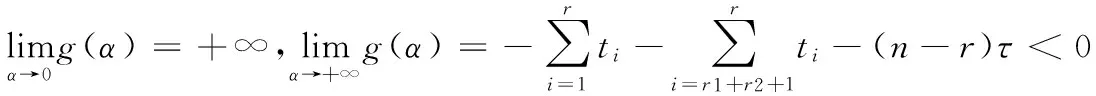

例2:取样本容量n=20,r=18,r1=7,r2=7,两个单元的失效率都取为α=0.01,通过Monte-Carlo模拟如表2所示的随机数。

表2 n=20,r=18,r1=7,r2=7,α=0.01的随机数
取τ=166.255 5,利用本文方法可得参数α的极大似然估计为:α=0.013 1。
例3:取样本容量n=20,r=18,r1=6,r2=8,两个单元的失效率分别取为α1=1,α2=1.5,通过Monte-Carlo模拟如表3所示的随机数。
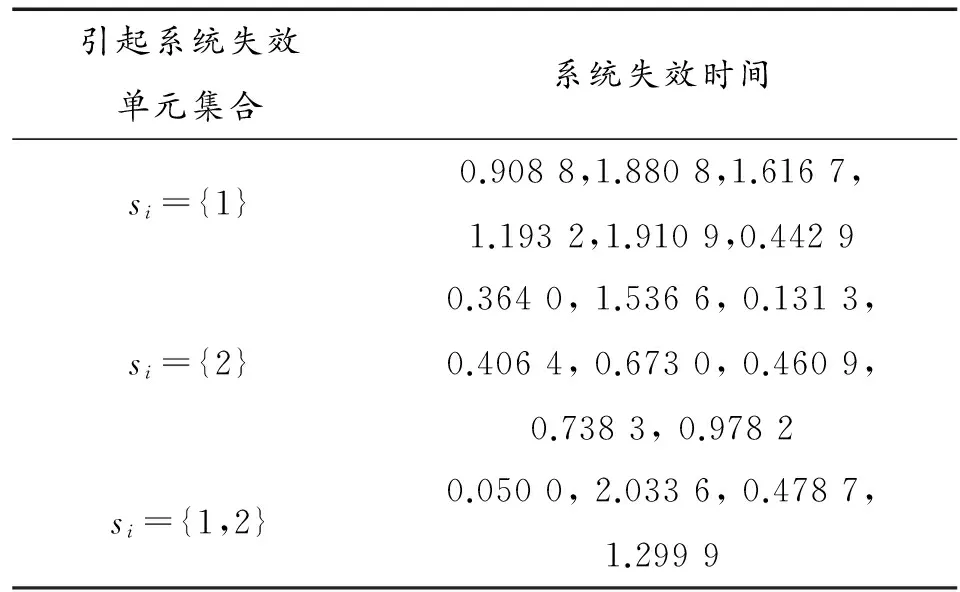
表3 n=20,r=18,r1=5,r2=10,α1=1,α2=1.5的随机数
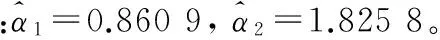
[1]JOHNS,USHER,THOMJ.HODGSON.MaximumLikelihoodAnalysisofComponentReliabilityUsingMaskedSystemLife-TestData[J].IEEETransactionsonReliability,1988,37(5):550.555.
[2]REISERB,GUTTMANI,DENNISK,etal.Usher-BayesianInferenceforMaskedSystemLifetimeData[J].Appl.Statist.,1995,44(1):79-90.
[3]AMMARM.SARHAN,AHMEDH.El.Bassiouny.EstimationofComponentsReliabilityinaParallelSystemUsingMaskedSystemLifeData[J].AppliedMathematicsandComputation,2003,138:61-75.
[4]DONALDEHUTTO,THOMASMAZZUCHI,SHAHRAMSARKANI.Analysisofreliabilityusingmaskedsystemlifedata[J].InternationalJournalofQuality&ReliabilityManagement,2009,26(7):723-739.
[5]WANGRonghua,XUXiaoling,GUBeiqing.TheStatisticalAnalysisofParallelSystemforType-ICensoredTestUsingMaskedData[C]//RecentAdvanceinStatisticsApplicationandRelatedAreas.2ndConferenceoftheInternationalInstituteofAppliedStatisticsStudies.Qingdao,CHINA,2009:789-795.
[6]XUAncha,TANGYincai.AnOverviewonStatisticalAnalysisforMaskedSystemLifetimeData[J].ChineseJournalofAppliedProbabilityandStatistics,2012,28(4):380-388.
[7] 张士峰,邓爱民.含有屏蔽寿命数据的贝叶斯可靠性分析[J].战术导弹技术,2001(3):34-39.
[8] 张帆,师义民.基于屏蔽数据的航空电源系统可靠性分析[J].航天控制,2009,27(4):96=100.
[9] 刘英,师义民.屏蔽数据下航天器电源系统的可靠性的统计分析[J].航天控制,2010,28(2):70-74.
[10]刘英,师义民,王婷婷.基于屏蔽数据的部件可靠性指标的贝叶斯估计[J].数理统计与管理,2010,29(5):853-860.
[11]张萌,师义民,杨扬.屏蔽数据下并联系统广义指数部件的可靠性估计[J].信息与控制,2011,40(4):483-496.
(责任编辑 杨继森)
Statistical Analysis of New Model for Masked Data Under Parallel System
XU Xiao-ling1, WANG Rong-hua2, GU Bei-qing1
(1.School of Statistics and Information, Shanghai University of International Business and Economics, Shanghai 201620, China; 2.Mathematics and Science College, Shanghai Normal University, Shanghai 200234, China)
The new model of masked data was proposed for parallel system, which modifies original basic assumption. The corresponding likelihood function was derived on this basis. The maximum likelihood estimates of parameters were studied under full sample and type-II censored sample. The examples were illustrated to the feasibility of this method by Monte-Carlo simulations.
parallel system; masked data; likelihood function; maximum likelihood estimate
2016-10-28;
2016-11-30 基金项目:上海市教育委员会科研创新重点项目(14ZZ155);上海市教育委员会科研创新一般项目(14YZ080)
徐晓岭(1965—),男,博士,教授,主要从事应用统计研究。
10.11809/scbgxb2017.03.037
徐晓岭,王蓉华,顾蓓青.并联系统下屏蔽数据新模型的统计分析[J].兵器装备工程学报,2017(3):164-169.
format:XU Xiao-ling, WANG Rong-hua, GU Bei-qing.Statistical Analysis of New Model for Masked Data Under Parallel System[J].Journal of Ordnance Equipment Engineering,2017(3):164-169.
O213.2
A
2096-2304(2017)03-0164-06
