基于三参数威布尔分布的刹车胶囊可靠性分析
2017-04-05张显余葛子厚付长安
李 静,张显余,葛子厚,付长安
(空军航空大学,长春 130022)
【机械制造与检测技术】
基于三参数威布尔分布的刹车胶囊可靠性分析
李 静,张显余,葛子厚,付长安
(空军航空大学,长春 130022)
根据某大型轰炸机液压系统统计资料的153个液压刹车胶囊有效样本,应用三参数威布尔分布对该故障部件进行了可靠性数据处理和寿命评估分析,对比以往在工程上采用两参数威布尔分布分析航空装备构件可靠性寿命的结果。分析表明,采用三参数威布尔分布分析和评估所得结果与实际使用情况吻合度更高。
轰炸机;液压刹车胶囊;三参数威布尔分布;可靠性分析
某大型轰炸机液压刹车胶囊作为液压刹车系统的中心执行附件,用以保证刹车系统工作安全可靠。威布尔分布在可靠性工程中,因其具有较大的适应性而得到了广泛的应用,它的主要优点是利用有限的数据样本,给出精确的分析和预测结果[1]。
目前对已给出的寿命试验或现场观测数据进行可靠性分析与评估时,多采用简单易行的两参数威布尔分布,其参数估计常常带来较大误差。徐微[2]、伍建军[3]等针对两参数威布尔的可靠性分布模型,提出了新的方法对其参数进行了估计,郑锐[4]、于捷[5]等提出三参数威布尔分布的可靠性评价可以获得更精确的参数估计值。因此,对于具有以耗损失效为特征的机液零附件的寿命评估中,采用三参数威布尔分布进行拟合及参数估计,精度更高,较两参数威布尔分布,更能反映机械或气液产品故障可靠性的实际情况。
1 液压刹车胶囊故障统计与调整
液压刹车胶囊是某大型轰炸机液压刹车系统的中心执行附件,该附件结构品质和工作性能的好坏直接影响着飞机起飞着陆时的安全[6]。根据近几年来对某大型轰炸机液压刹车系统在外场使用和内场修理情况的跟踪统计,在本文统计的153个有效液压刹车胶囊样本中发现,有77个液压刹车胶囊因存在不同程度老化或裂纹故障而更换,占总数50.3%;使用到规定保管期无故障而更换的为76个,占总数49.7%。故障统计数据结果如表1[7]所示。

表1 故障统计数据结果
2 液压刹车胶囊可靠性数据处理
2.1 用残存比率法计算可靠度函数和故障失效分布函数
由残存比率法知[8]:
(1)
(2)
(3)
(4)
式中:ns(ti-1)为产品在ti-1时刻继续受试样本数;Δr(ti)为产品在ti-1~ti时间内故障数;n为观察样本总数;Δk(tj)为在时间区间tj-1~tj内删除的样本数。
根据统计数据,用残存比率法计算刹车胶囊可靠度函数和故障失效分布函数,其结果如表2所示。
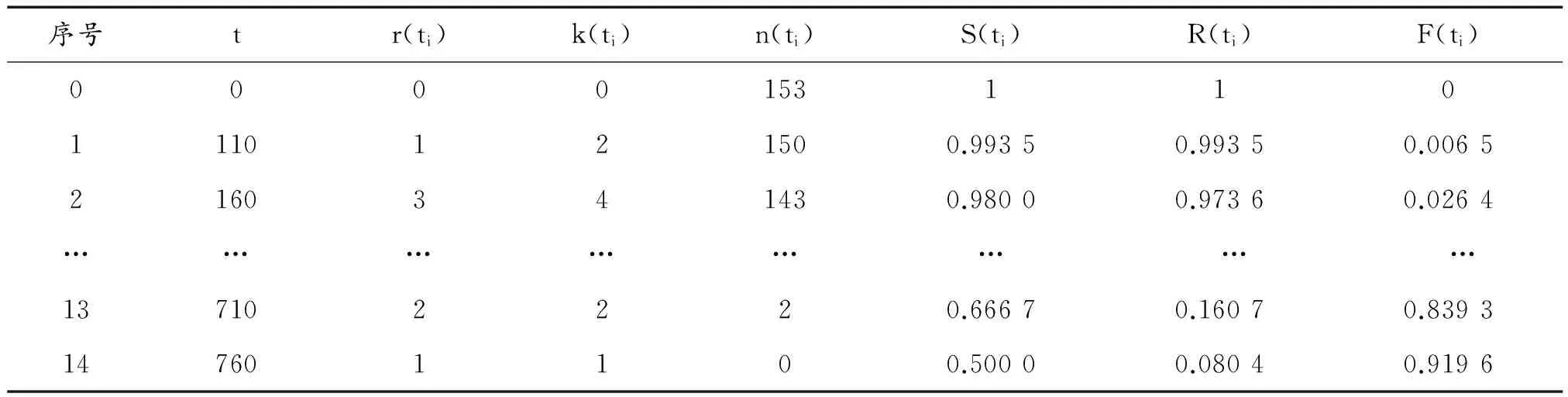
表2 可靠度函数和故障失效分布函数
2.2 用最小二乘法确定液压刹车胶囊故障分布估算参数和寿命特征值
假设液压刹车胶囊故障服从威布尔分布,用三参数威布尔分布对液压刹车胶囊故障分布进行分析[9-10],则故障分布函数为
(5)
式中:t≥t0,η>0,m>0;t0为位置参数,当t0=0时,即为两参数威布尔分布;η为尺度参数;m为形状参数(m值决定密度曲线的形状)。
对等式两边取对数,整理得
(6)
令x=lnln[1-F(t)]-1, y=ln(t-t0), a=1/m, b=ln(η-t0)
则式(6)可化简为线性方程
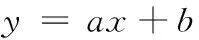
(7)
将表2中的F(ti)值代入式x=lnln[1-F(t)]-1中可得xi,其结果如表3所示。
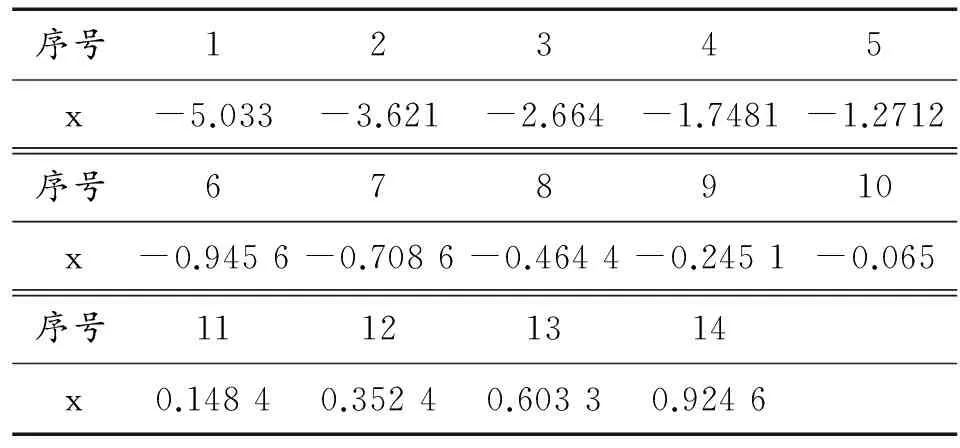
表3 各时间节点对应的x值
假设t0i为最小寿命,取t01=110,步长Δ=0.05,t01=5.5,令t0i=t0i-1-Δ,用假设最小寿命t0i代替三参数威布尔分布的累积故障分布函数的最小寿命t0,然后代入式y=ln(ti-t0)中得出yi值如表4所示。
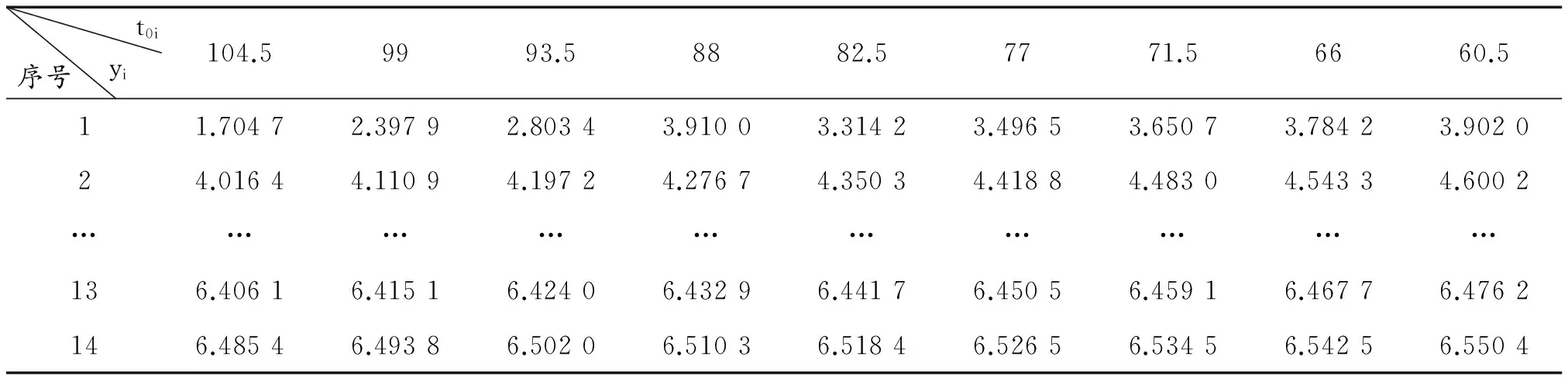
表4 各时间节点及假设最小寿命对应的y值
采用最小二乘法回归直线,得式(6)线性回归方程y=ax+b的回归系数表达式分别为:
且x与y的相关系数的表达式为
(10)
将所求xi和yi代入式(10)得一组ρ值,分别为:
ρ01=0.989 7, ρ02=0.992 6, ρ03=0.994 5
ρ04=0.995 9, ρ05=0.996 2, ρ06=0.996 8
ρ07=0.997 0, ρ08=0.997 7, ρ09=0.997 5
由三参数威布尔分布知,当ρ0i取最大值时,对应的t0i所确定的直线对数据点的拟合最佳,因此,取ρ=max(ρ0i)=0.997 7,它对应的位置参数t0=66,将其所对应的一组xi,yi代入式(8)、式(9)中,得:a=0.471,b=6.178。
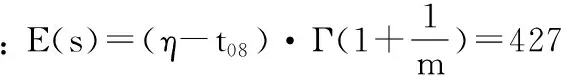
用K-S检验判别故障分布的正确性。取置信度1-α=0.95,计算理论分布和经验分布的差异度为:
(i=1,2,… n)
查表得:λ=1.36,因λn<λ,故接受假设,故障分布服从参数为m=2.123,η=548的威布尔分布。
3 故障率和可靠寿命的计算
根据威布尔分布的数学模型知故障率函数为
(11)
由计算可得λ(ti),如表5所示。

表5 不同时间节点对应的故障率

表6 不同R(ti)对应的可靠寿命t(R)
4 结论
1) 三参数威布尔分布较两参数威布尔分布时形状参数m偏小,计算结果精确度更高,更能反映产品可靠性的实际情况。
2) 该刹车胶囊可靠寿命较低,而且附件故障主要取决于系统工作环境和使用维护质量。从使用寿命和安全角度出发,合理掌握使用和检查时机,尤其在炎热季节及附件接近规定使用期限内应加强检查,提高外场维修品质和管理水平。
[1] 王海涛,陈星,段斐翡.三参数威布尔分布模型在系统的可靠性评估中的应用[J].机械与电子,2015(3):78-80.
[2] 徐微,胡伟明,孙鹏.基于两参数威布尔分布的设备可靠性预测研究[J].中国工程机械学报,2013,2(11):112-116.
[3] 伍建军,游雄雄,吴事浪,等.两参数威布尔分布的废旧矿冶零部件再制造剩余寿命预测新方法[J].机械科学与技术,2016,4(35):589-593.
[4] 郑锐.三参数威布尔分布参数估计及在可靠性分析中的应用[J].振动与冲击,2015,5(34):78-81.
[5] 于捷,申桂香,贾亚洲.基于三参数威布尔分布的数控机床的可靠性评价[J].现代制造工程,2007(5):18-20.
[6] 付长安,张显余.某型轰炸机构造与维护[M].长春:空军装备部出版,2014.
[7] 张显余.某型轰炸机液压刹车胶囊可靠性分析[J].长春:航空学院学报,2003(2):12-15.
[8] 贺国芳.可靠性数据的收集与分析[M].北京:国防工业出版社,2003.
[9] 方志强,高连华.三参数威布尔分布在寿命分析中的应用[J].可靠性工程,2002(8):25-28.
[10]刘瑞元.三参数威布尔分布在寿命分析中应用时的一些论证[J].可靠性工程,2002(5):53-56.
(责任编辑 唐定国)
Reliability Analysis on Brake Capsule Based on Three-Parameter Weibull Distribution
LI Jing, ZHANG Xian-yu, GE Zi-hou, FU Chang-an
(Aviation University of Air Force, Changchun 130022, China)
According to the statistics of 153 hydraulic brake capsule effective samples about a large bombers hydraulic system, we used three-parameter weibull distribution for reliability data processing and life assessment analysis on the fault component, and contrasted the past results on the engineering analysing of the reliability life of the aviation equipment component based on two-parameters weibull distribution, and the result of using three-parameters weibull distribution analysis and evaluation has higher fitness with the actual usage.
bomber; hydraulic brake capsule; three-parameter weibull distribution; reliability analysis
2016-10-20;
2016-11-21 作者简介:李静(1992—),男,硕士研究生,主要从事飞行器设计液压与气压传动可靠性分析研究;E-mail:1399383030@qq.com。
张显余(1959—),男,教授,硕士生导师,主要从事飞机结构强度、液压与气压传动结构等方面的理论研究与教学。
10.11809/scbgxb2017.03.031
李静,张显余,葛子厚,等.基于三参数威布尔分布的刹车胶囊可靠性分析[J].兵器装备工程学报,2017(3):134-136.
format:LI Jing, ZHANG Xian-yu, GE Zi-hou, et al.Reliability Analysis on Brake Capsule Based on Three-Parameter Weibull Distribution[J].Journal of Ordnance Equipment Engineering,2017(3):134-136.
V215.7
A
2096-2304(2017)03-0134-03
