Lamb波频散特性和波结构特性的有限元仿真
2017-04-05袁培龙周绍骑李学新
袁培龙,周绍骑,李学新,唐 航
( 后勤工程学院 军事供油工程系,重庆 401331)
【机械制造与检测技术】
Lamb波频散特性和波结构特性的有限元仿真
袁培龙,周绍骑,李学新,唐 航
( 后勤工程学院 军事供油工程系,重庆 401331)
采用ANSYS有限元仿真软件模拟超声Lamb波在4 mm厚的钢板结构中的传播过程,计算S0模态和A0模态超声Lamb波的群速度和沿钢板厚度方向上的位移波结构,绘制频散曲线和波结构特性曲线,理论分析与仿真结果基本吻合;为超声Lamb波群速度测定和缺陷检测提供理论依据。
Lamb波;频散;波结构;有限元;传播规律
超声Lamb波作为超声导波的一种,主要存在于平板结构中,具有易于激励、对初始损伤和微小缺陷敏感、传播距离远、检测精度不受平板表面流体影响等优点,是目前检测平板缺陷极具前景的无损检测手段之一[1]。超声Lamb波是一种特殊的体波,其频散特性和多模式特点决定了其在激励、传播、接收和质点振动方式上的复杂性[2-4]。因此,研究Lamb波的频散特性和波结构特点,进而依据其频散特性曲线和波结构特性曲线选取一定频厚积下合适模态的超声Lamb波进行缺陷检测显得尤为重要[5-9]。目前,超声Lamb波频散特性和波结构特性上的研究多为理论分析,基于有限元仿真的方法分析超声Lamb波频散特性和波结构特性的较少。
本文首先对超声Lamb波的频率特性方程进行数值求解并绘制其频散特性曲线和波结构特性曲线。基于ANSYS 有限元分析的方法在钢板模型中仿真超声Lamb的传播过程,提取仿真数据结果,计算不同频厚积下A0模态和S0模态的群速度,绘制有限元仿真情况下的频散曲线和波结构曲线。理论分析与仿真结果对比验证了有限元法的有效性。
1 超声Lamb波的理论分析
超声Lamb波在金属平板内传播过程中其质点运动位移满足Navier质点平衡方程:
(1)
式(1)中u为质点振动位移矢量,μ、λ为Lame常数。
根据金属平板中质点的振动特点可分为对称模态(S)和反对称模态(A)。在不同相速度下的超声Lamb波存在不同阶次的模态,用S0、S1、S2、S3、S4…A0、A1、A2、A3、A4…表示。根据势函数求解法求解质点平衡方程,得到Lamb波位移场表达式:
对称模态:
(2)
反对称模态:
(3)
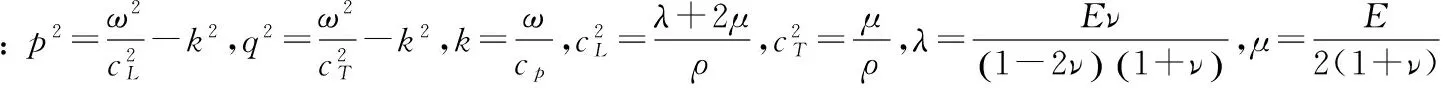
其中,μ 为离面位移,ν为面内位移,ω为角频率,cL、cT分别为钢板中的纵波波速和横波波速,k为波数,E和G是钢板弹性模量和剪切模量,υ为泊松比; ρ为钢板密度。
根据零应力边界条件可求得A1、A2、B1、B2,即可计算得出Rayleigh-Lamb频率方程:
对称模态:
(4)
反对称模态:
(5)
2 超声Lamb波频散特性曲线和波结构特性
2.1 超声Lamb波的频散特性曲线
Rayleigh-Lamb频散方程决定了超声Lamb波存在多模态和频散现象,下面以对称模态为例,求解Rayleigh-Lamb频散方程:
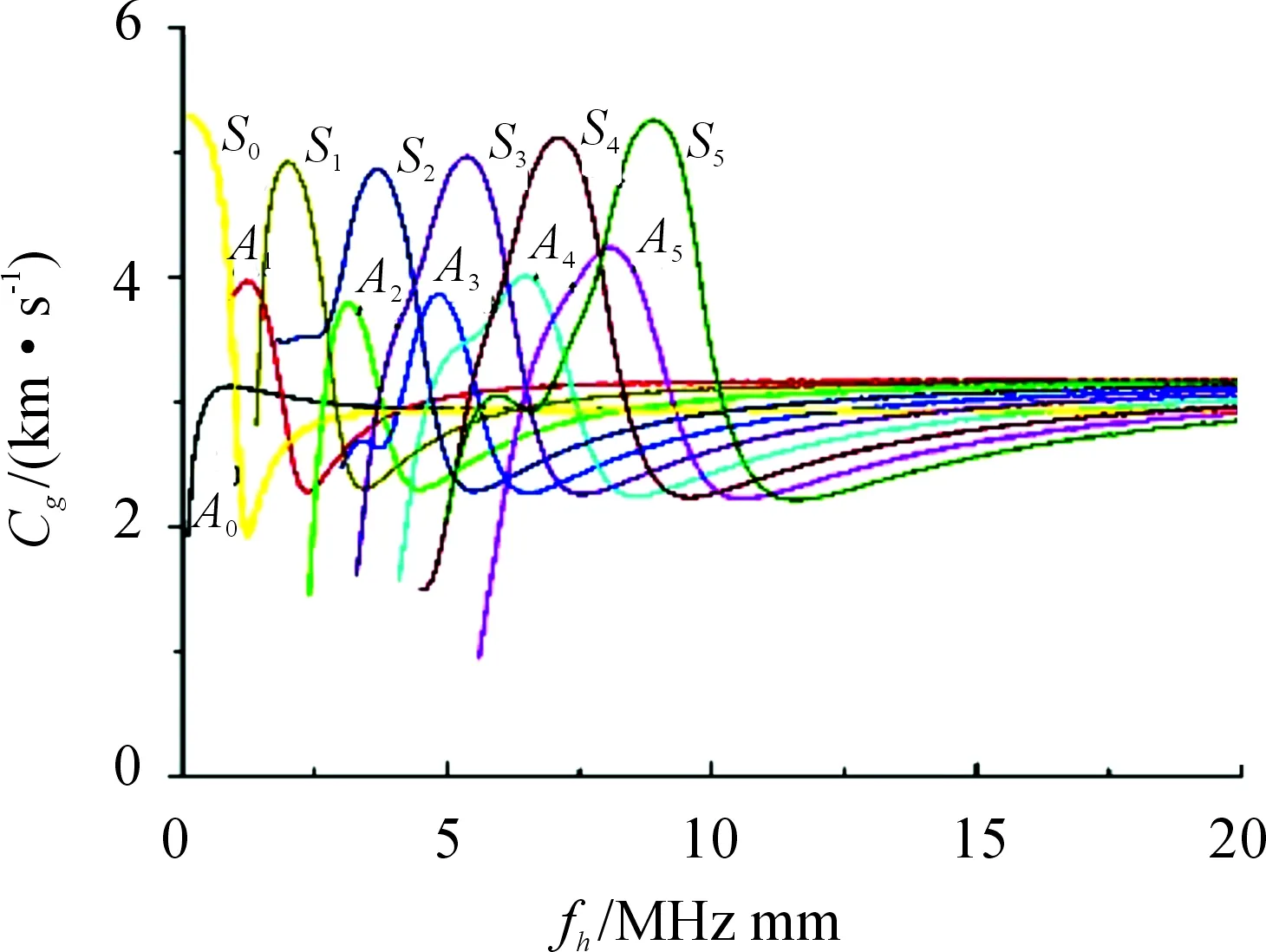
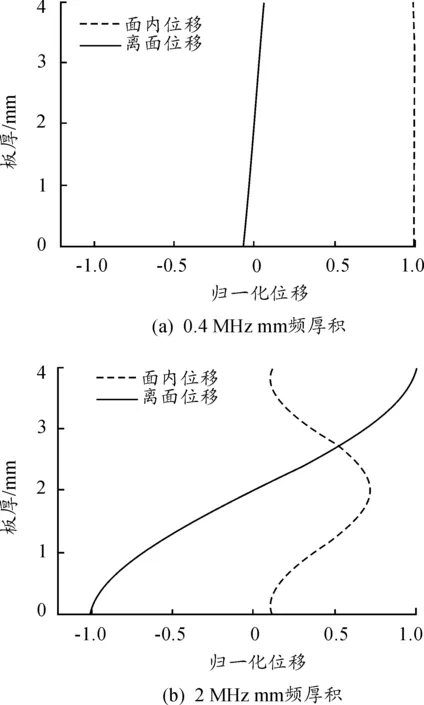
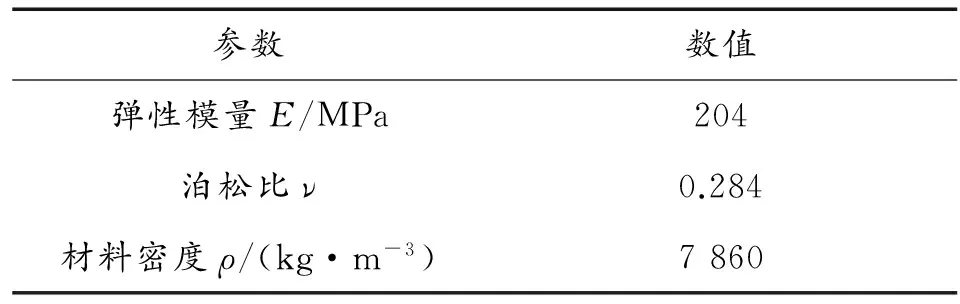
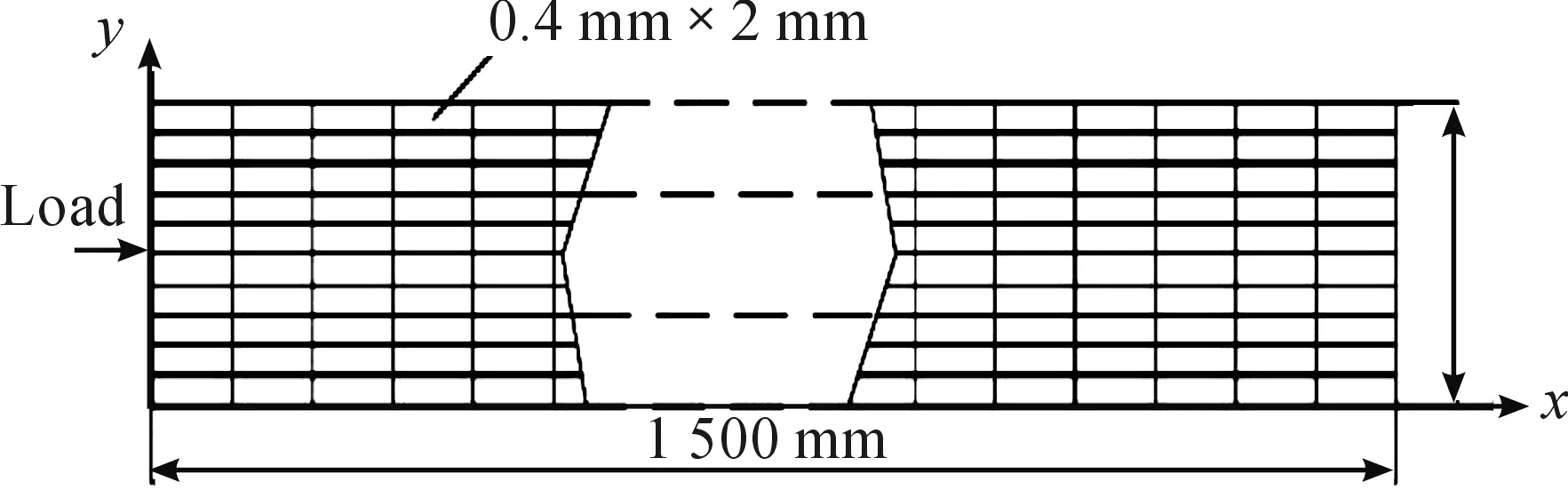
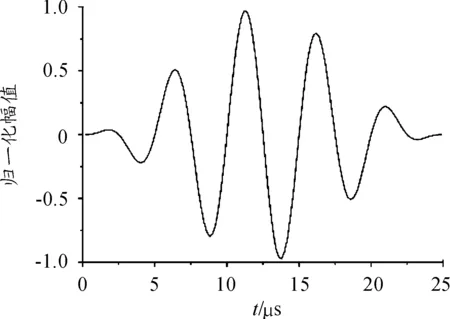
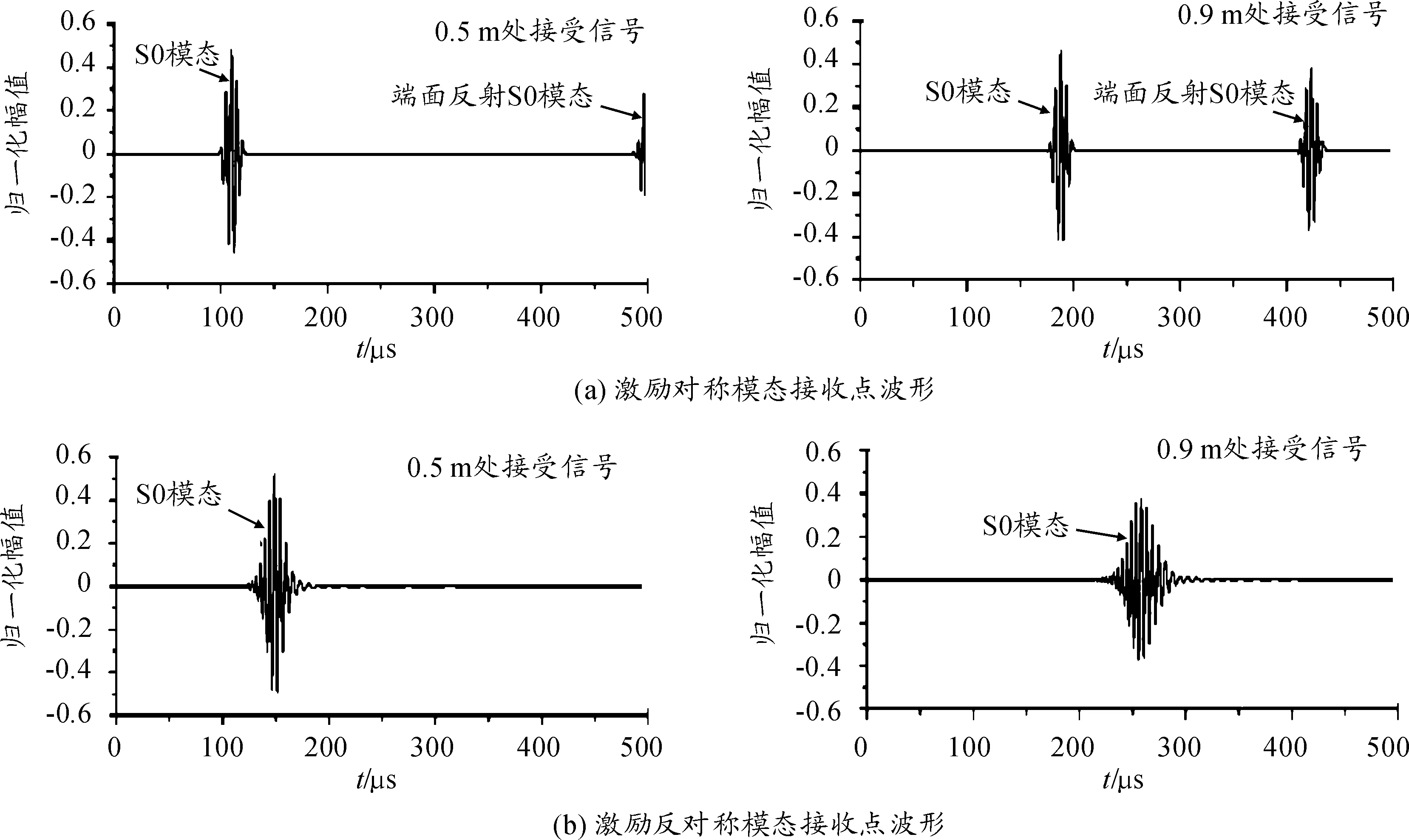
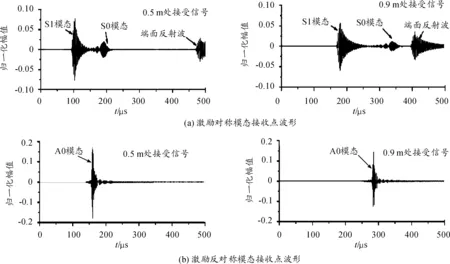
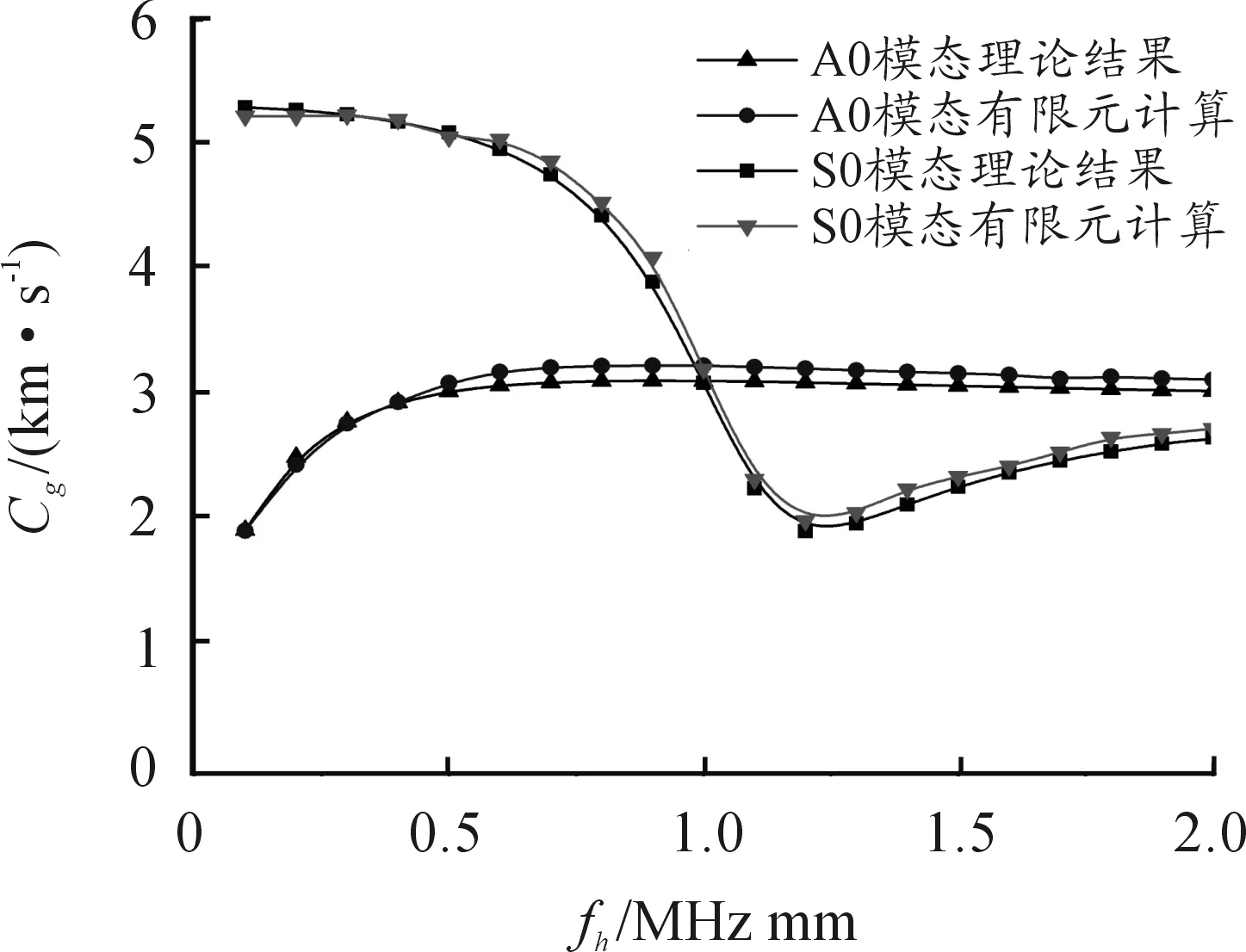
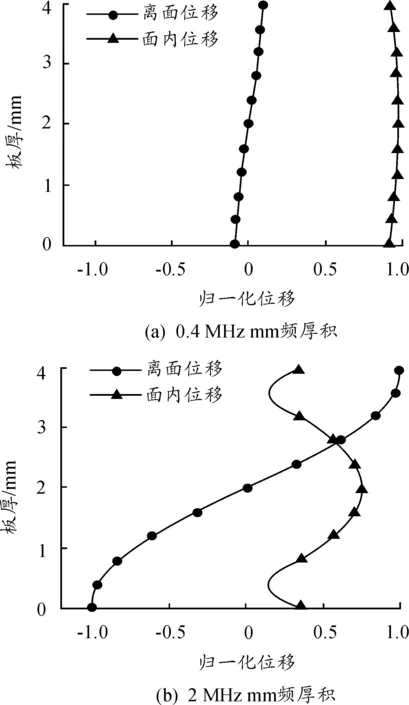
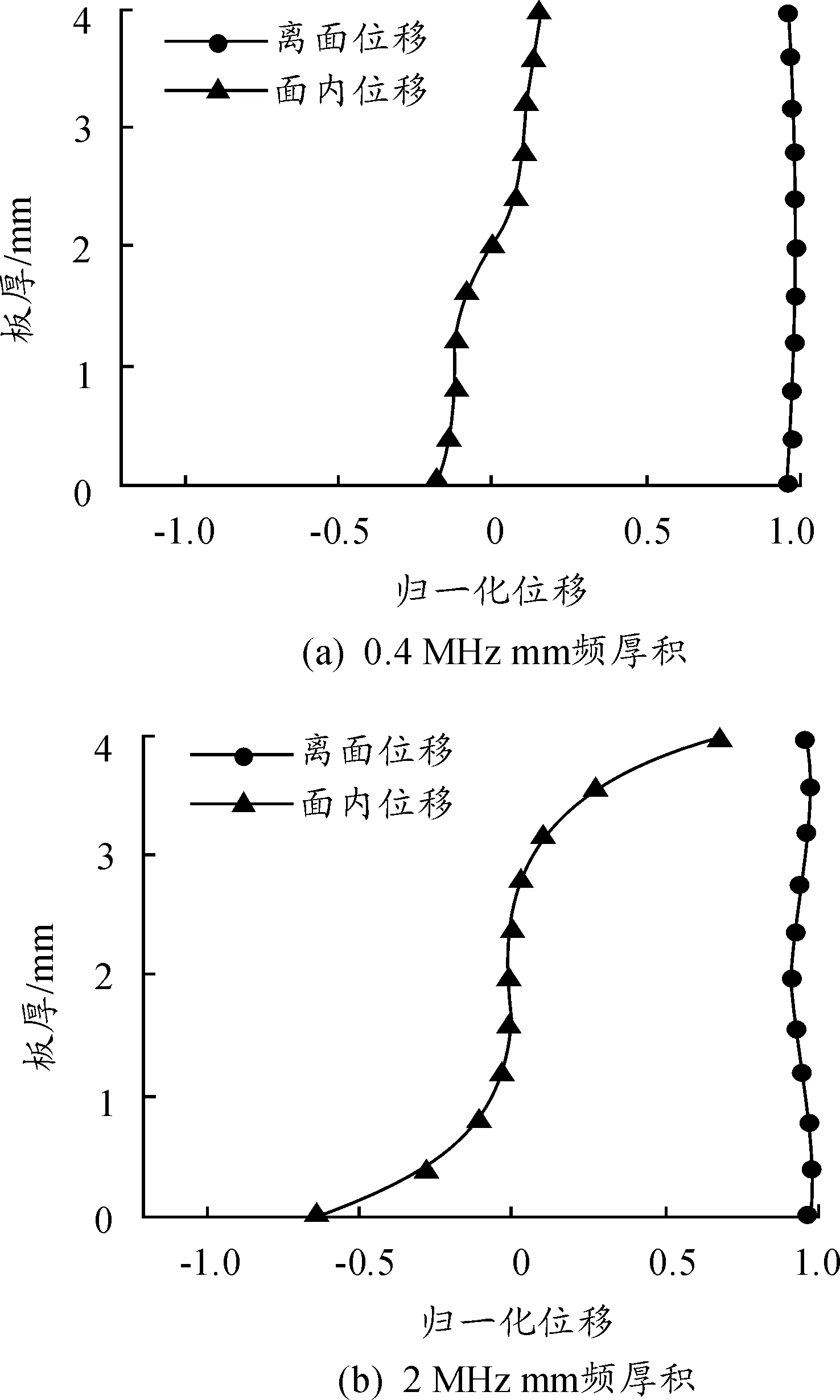
各项同性材料的金属板中cl>ct,当cp>cl时式(4)中分子分母都在实数范围之内,当cp 1) 当0 (5) (6) 2) 当ct (7) (8) 3) 当cl (9) 编写Matlab计算程序使相速度cp和频厚积fd以一定的时间步长在分析范围内迭代求解,采用二分法通过对比y变量的变化计算出对应频厚积下的相速度。钢板中纵波波速5.790 km/s,横波波速3.180 km/s,绘制出超声Lamb波的频散特性曲线如图1、图2所示。 图1 钢板中Lamb波的相速度曲线 图2 钢板中Lamb波群速度曲线 由超声Lamb波频散特性曲线可以看出,同一频厚积下可以产生两种或两种以上模态,且群速度不同;不同模态下的超声Lamb波均存在频散现象,其相速度和群速度均随频厚积的变化而变化;除S0、A0模态外其余模态均存在截止频率。 2.2 超声Lamb波的波结构特性曲线 在各向同性钢板中通过给定的模态Lamb波的频厚积和相速度,由式(2)、式(3)可推导求解计算其沿厚度方向的离面位移和面内位移,图3、图4为频厚积为0.4 MHz mm和2 MHz mm时S0模态和A0模态超声Lamb波的波结构示意图。在此对其进行归一化处理。 图3 S0模态位移波结构示意图 从图4可以看出,对称模态的Lamb波沿钢板厚度方向面内位移关于板中心对称,离面位移关于板中心反对称。反对称模态Lamb波,沿钢板厚度方向离面位移关于板中心对称,面内位移关于板中心反对称。在低频厚积下S0模态以面内位移为主,离面位移为辅;A0模态以离面位移为主,以面内位移为辅。随频厚积增加,对称模态的离面位移和反对称模态的面内位移在板中逐渐增加,对称模态的面内位移和反对称模态的离面位移逐渐减小。 采用有限元仿真软件ANSYS仿真超声Lamb波在4 mm厚、1 500 mm长的钢板中传播,钢板模型材料特性参数如表1所示。 表1 有限元仿真钢板材料特性参数 图5 有限元仿真模型示意图 3.1 激励信号选取 为减少Lamb波在传播过程中的能量泄漏,提高计算精度,本文采用汉宁窗加载函数调制5周期正弦信号作为激励信号。将激励信号中心频率从25 kHz逐步增加至500 kHz,对应频厚积从0.1 MHz mm增加至2 MHz mm。图6为中心频率为200 kHz的激励信号波形图,对波形幅值统一进行归一化处理。 图6 中心频率200 kHz激励信号波形 3.2 有限元仿真结果分析 根据Lamb波的波结构理论分析知,在钢板一端的中间节点以一定的中心频率加载面内位移可以激励产生对称模态信号;加载离面位移可激励产生反对称模态信号。 在距离加载端面0.5 m和0.9 m处的钢板表面设置信号接收点,设置加载信号中心频率为200 KHz。图7(a)为加载面内位移激励产生对称模态Lamb波后接收点波形,根据群速度判断为S0模态Lamb波,图中接受信号的第二个波形为平板端面反射波,计算时间范围内,0.5 m处反射波未能完整显示。图7(b)为加载离面位移激励产生反对称模态超声Lamb波后接收点波形,根据群速度判断为A0模态Lamb波,由图可以看出A0模态在传播过程中时间扩张较为明显,在计算时间范围内接收点没有出现端面反射波信号。 理论分析可知,改变激励信号中心频率后,超声Lamb波的将会发生频散现象,图8(a)为加载中心频率500 kHz面内位移激励产生对称模态超声Lamb波后接收点波形,图8(b)为加载中心频率500 kHz离面位移激励产生反对称模态超声Lamb波后接收点波形。由图可以看出,频厚积为2 MHzmm时,对称模态和反对称模态Lamb波在传播过程中均发生频散现象,对称模态Lamb波比反对称模态Lamb波频散现象更为明显,且对称模态发生明显模态分离现象。 采用ANSYS有限元仿真的方法可以在钢板中激励出单一模态的超声Lamb波,随频厚积增加Lamb波在钢板中传播时会发生频散现象和模态分离现象。采用ANSYS有限元仿真的方法适合激励较低频厚积下的超声Lamb波。 图7 加载中心频率200 kHz接收点波形 图8 加载中心频率500 kHz接收点波形 3.3 有限元仿真分析超声Lamb波的频散特性 超声Lamb波在钢板中向前传播时,激励信号以群速度作为能量传播的速度。通过计算相应波包峰值的前进速度可以计算出对应模态的群速度: (10) 式(10)中D为选定的两个接受信号节点的距离,Tp1、Tp2为采集到时域脉冲信号的对应模态波峰的时刻。 根据采集到接收点波形信号,可计算出S0和A0模态的超声Lamb波群速度,图9为理论值与仿真值对比示意图。 图9 群速度理论值与仿真比示意图 将有限元方法计算出的群速度值与理论群速度进行比较,计算误差均小于5%。在误差允许范围内,利用ANSYS有限元仿真的方法可较精确的计算钢板中不同模态和频厚积下的群速度值。 3.4 有限元仿真分析超声Lamb波的波结构特性 在钢板模型中距离端面0.5 m处沿厚度方向每间隔0.4 mm设置一个信号接收点,分别得出沿厚度方向S0模态A0模态离面位移和面内位移波形变化规律,对节点处位移进行归一化处理,可得出有限元仿真时位移波结构示意图,如图10、图11。 图10 S0模态位移波结构仿真结果示意图 图11 A0模态位移波结构仿真结果示意图 图10、图11可以看出,采用有限元分析的方法研究Lamb波在钢板厚度方向上的位移波结构变化规律与理论计算结果基本吻合,有限元仿真的方法可直观分析Lamb波的波结构特性,进而研究不同模态和频厚积下Lamb波穿透结构的能力,实现对钢板缺陷的检测。 本文通过理论分析和有限元仿真相结合的方法对钢板结构中超声Lamb波的传播规律、频散现象和波结构特点进行研究,理论计算与有限元仿真基本吻合,理论分析为检测钢板厚度和波速测定提供依据,有限元仿真可以更加直观分析Lamb波的频散特性和波结构特性,为观察单一模态Lamb波在钢板结构中传播和穿透结构的能力提供有力工具。 [1] 周正干,冯海伟.超声导波检测技术的研究进展[J].无损检测,2006,28(2);57-63. [2] 张燕,龚立娇.Lamb波频散特性的数值仿真研究[J].压电声光,2014,36(5);701-704. [3] 艾春安,工学勇,刘瑜.薄板钢结构超声检测Lamb波激励与模态分析[J].噪声与振动控制,2012,32(1):137-140. [4] XU Kailiang,TA Dean,SU Zhongqing,wang Weiqi.Transmission Analysis Of Ultrasonic Lamb Mode Conversion In A Plate With Partial-thickness Notch[J].Ultrasonics,2014,54(11):395-401. [5] 刘长福,牛晓光,李中伟,等.基于ANSYS的超声纵/横波传播仿真计算[J].无损检测,2011,33(6):15-18. [6] 张海燕,曹亚萍,于建波,等.采用单个压电传感器的单模式兰姆波激发频率的选择[J].物理学报,2011,60(11):377-385. [7] 李引凡.短波车载半环天线仿真分析[J].重庆工商大学学报(自然科学版),2015,32(10):63-67. [8] 吴斌,周伟,郑阳.等.基于波结构的Lamb波单一模态激励仿真[J].无损检测,2011,33(7):1-4. [9] YOJI O,KEIJI F.Delamination Detection In Composite Laminates Using Dispersion Change Based On Mode Conversion Of Lamb Waves[J].Smart Materials and Strurturcs,2010,19(11):1-11. [10]NG C T,VEIDT M,ROSE L R F,et al.Analytical And Finite Element Prediction Of Lamb Wave Scattering At Delaminations In Quasi-isotropic Composite Laminates[J].Journal of Sound and Vibration,2012,331(5):4870-4883. [11]廖肖晓,周绍骑,白金春.三轴交流漏磁检测矩形缺陷信号特征分析[J]. 重庆理工大学学报(自然科学),2016(9):106-112. [12]高望,张金,王瑾珏.火炮身管无损检测方法[J].火力与指挥控制,2015(7):16-19. (责任编辑 唐定国) Finite Element Simulation of Lamb Wave Dispersion Characteristics and Wave Structure Features YUAN Pei-long, ZHOU Shao-qi, LI Xue-xin, TANG Hang (Department of Military Petroleum Supply Engineering, Logistical Engineering University of PLA, Chongqing 401331,China) The propagation process of A0 and S0 mode wave in 4 mm steel plate was simulated in finite element simulation software ANSYS, and group velocity curves and wave structure characteristic curves of S0 and A0 Lamb waves in steel plate were plotted. Simulation results are approximately agreed with the theoretical analysis. It provides theoretical basis for group velocity measurement and defect detection. Lamb wave; dispersion; wave structure; the FE method; propagation law 2016-07-14; 2016-10-15 基金项目:重庆市重点科技攻关项目(cstc2012gg-sfgc00002) 袁培龙(1992—),男,硕士研究生,主要从事超声导波检测技术方向研究。 10.11809/scbgxb2017.03.032 袁培龙,周绍骑,李学新,等.Lamb波频散特性和波结构特性的有限元仿真[J].兵器装备工程学报,2017(3):137-142. format:YUAN Pei-long, ZHOU Shao-qi, LI Xue-xin, et al.Finite Element Simulation of Lamb Wave Dispersion Characteristics and Wave Structure Features[J].Journal of Ordnance Equipment Engineering,2017(3):137-142. TB553 A 2096-2304(2017)03-0137-06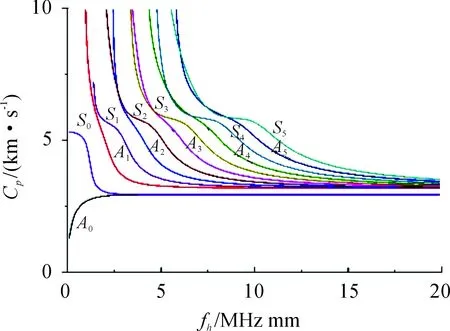
3 超声Lamb波传播规律的有限元仿真
4 结论
