球形装药爆腔预测的准静态模型*

于成龙,王仲琦

(北京理工大学爆炸科学与技术国家重点实验室,北京100081)

球形装药爆腔预测的准静态模型*

于成龙,王仲琦

(北京理工大学爆炸科学与技术国家重点实验室,北京100081)

炸药土中爆炸形成爆腔的特征尺寸会影响远场地震波的幅频特征。为了准确预测爆腔的特征尺寸,本文建立了爆腔膨胀的准静态模型,该模型给出了无限均匀不可压缩的弹性介质中球形装药爆炸形成的粉碎区、裂隙区半径的解析表达式,并利用该模型计算讨论了不同条件下各分区尺度的变化。最后将该模型与现场实验、动力模型所得到的结果进行对比后表明,该模型与以上两者之间的误差约为5.4%～16.0%,能够较为准确地预测爆腔尺寸。

球形爆腔;准静态理论;粉碎区;裂隙区

地震勘探理论中将爆炸震源等效为一个球形空腔,假设初始时刻在空腔内表面施加均匀的径向压强,进而得出远场地震波的特征。R.F.Favreau[1]建立了远场地震波振动速度、粒子径向位移以及环向位移与空腔半径的解析表达式,通过建立模型预测爆炸产生破坏区域的半径从而得到远场地震波的特征。

目前针对封闭爆炸条件下爆腔特征尺寸的计算理论有半经验方法、准静态理论以及爆腔的动力理论等[2]:(1)半经验理论是爆破理论发展初期为了获得更好的爆破效果所建立的一些经验公式[3-6],该方法计算简便但计算误差较大;(2)准静态理论即通过爆炸前后的绝热关系来求解爆腔形成后的最终尺寸,利用该方法能够对一些土中爆炸问题进行分析[7],但是无法展现出爆腔形成的动态过程;(3)利用爆腔的动力理论不仅能够计算出爆腔终态的特征尺寸,还能够模拟出爆腔的形成过程,因此受到较大的关注[8-9],但动力理论在计算爆腔特征尺寸的过程中需要确定许多复杂的参数,同时该方法计算过程复杂、耗时较长。

因此需要建立一套计算准确、求解速度快,能够应用于实际工程中的爆腔特征尺寸计算方法。利用准静态理论建立破坏区域的分区模型不仅计算速度快,还能够在很大程度上反应破坏区域的动态形成过程,M.F.Drukovanyi等[10]基于准静态理论建立了柱形装药的爆腔预测模型,该模型给出了均匀、不可压缩的无限弹性介质中的柱形装药爆炸形成粉碎区、裂隙区半径的解析表达式。但是该模型主要应用于药包长径比较大的矿山爆破中,而地震勘探往往采用球形或长径比小于3～5的柱形药包,这类药包爆炸后会产生的地震波通常以近似球面波的形式传播。

对此,本文中通过准静态理论推导球形装药条件下爆腔特征尺寸的解析模型,利用模型能够计算不同破坏区域最终的尺寸,并通过与实验数据及动态爆腔模型计算结果进行对比,验证该模型能够较为准确地预测爆腔特征尺寸。

1 球形装药准静态模型建立

炸药从爆炸到最终在远场形成弹性波的过程伴随着一系列的化学与物理变化过程。由于各种耗散机制的作用,能量在传递过程中不断衰减,由最初具有很强能量的冲击波演变为最终的弹性波。同时在衰减的过程中介质在强爆炸的作用下会发生一些不可逆的变形,在能量传递方向上依次形成爆炸空腔、粉碎区、裂隙区和弹性区(如图1所示)。

相关研究表明:远场地震波信号主要来源于炸药爆炸引起的爆炸区邻近范围内地质结构的自振[11],且远场地震波的传播距离远远大于爆炸产生的爆腔半径,因此爆腔的动态形成过程对于远场地震波信号的影响可以忽略不计。因此可以对这一复杂的波动过程进行简化,本文中通过爆炸前后的平衡关系建立了球形装药爆腔形成的准静态模型。模型中做出如下假设:(1)岩土介质是不可压缩的; (2)炸药爆炸对岩土介质密度的改变忽略不计;(3)爆炸空腔和破坏区域的形成是瞬时的;(4)炸药的爆轰过程是瞬时的。

图1 球形爆腔响应区Fig.1 Response regions in a spherical cavity

如图1所示,其中am为空腔半径,b*为破碎区半径,b0为裂隙区半径,可将整个区域分为3个部分[10]:

(1)弹性变形区域:b0(t)≤r≤∞;

(2)径向破裂区域:b*(t)≤r＜b0(t);

(3)完全破碎区域:am(t)≤r＜b*(t)。

1.1 弹性区

基于以上假设,在弹性介质中球形爆腔的扩腔的条件下切应力为零,环向应力相等,因此平衡方程可简化为

式中:σr为径向应力,σφ为环向应力,r为粒子的爆心距。则应变ε可由径向位移u表示:εr=du/dr和εφ=u/r,弹性变形区域中应用虎克定律,其一般形式可写为

式中:μ和λ为拉梅系数、θ为体应变,将平衡方程中的应力用位移表示

式中:前一部分中体应变为0,在弹性区域的内边界中切应力受限于岩体的抗拉强度(σ0),径向位移在弹性区域变为

因此在弹性区中,边界b0上的位移u0可以写成

1.2 径向破裂区

在径向破裂区中环向应力为0,则平衡方程为

在区域3边界σr(b0)=-σ0,在区域1边界上σr(b*)=-σ*,σ*为抗压强度。对式(6)进行积分可得

则区域2在边界b*上有由应力应变关系σr=2μεr可得

1.3 粉碎区

在粉碎区部分,岩土介质与炸药紧密接触,爆炸产生的瞬时压力远大于岩土的抗压强度。因此在这一区域中,介质会出现巨大的塑性变形及断裂破碎等现象。目前针对这一区域的预测存在很大分歧,普遍认为该区域的半径约为装药半径的3～5倍。为了描述粉碎区岩土介质的破坏,本文中采用了引入黏聚力的颗粒状不可压缩介质模型。简化的库伦定律为

式中:τmax为剪切强度,f为内摩擦因数,k为内聚力。破坏时的剪切应力为最大剪切应力,正应力为σ= (σφ+σr)/2,通过不可压缩的最优条件,其关系为σz=(σφ+σr)/2,将其代入式(9)后得到

式中:α=(1-f)/(1+f),β=2k/(1+f),将上式代入平衡方程,由边界条件:r=b*,σr=-σ*可得

而腔壁上的压力为

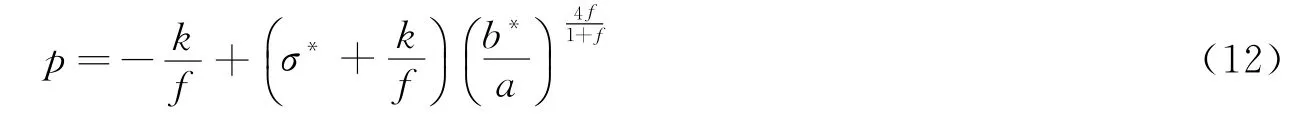
由不可压缩条件

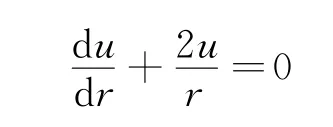
在边界r=b*上进行计算,得到

式中:L=2μ/σ*,由于a≫a*,所以

则爆压pm在最大的爆腔内为

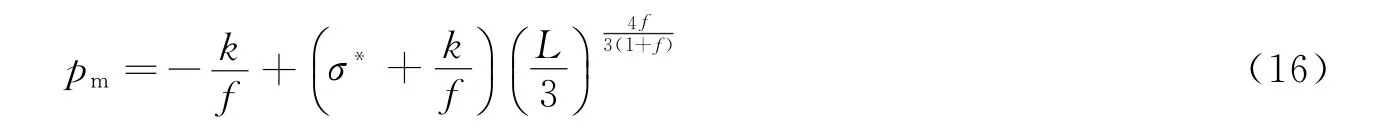
根据绝热定律,爆腔上的压力关系为pm(am)3γ=p0(a0)3γ,其中a0为装药半径,p0为初始爆炸瞬时压力,γ为炸药膨胀指数,爆腔的最大半径由下式给出

可以得到最大粉碎区域b*的大小为

径向裂隙区的范围b0为

2 讨 论

2.1 算例

对TNT在普通砂质黏土中爆炸进行计算,其中TNT与粉砂岩的相关特性参数见表1和表2。利用第1节中准静态模型进行计算,结果显示爆炸形成的粉碎区半径b*为0.36 m,裂隙区半径b0为0.69 m,空腔形成时爆腔内的残余压力为19.9 MPa。

表1 TNT特性参数Table 1 Parameters of TNT

表2 砂质黏土特性参数Table 2 Parameters of Sandy-clay

根据公式(7)、(10)、(14)可以计算出整个空间内的应力分布,以TNT在砂质粘土中爆炸为例对介质中的径向应力分布进行计算,结果如图2所示。从图2中可以看出,介质受到的径向应力从空腔壁处开始一直延续到无限远处。在整个区域中空腔壁处受到的径向应力最大,该点的具体数值由炸药性质和岩土介质的抗压强度共同决定;在粉碎区内介质发生了永久变形,径向应力迅速衰减。在粉碎区与裂隙区的交界处,由于爆炸压力减小,介质由永久变形转变为塑性变形,应力衰减速度降低;当压力小于介质的抗拉强度后,介质不会发生破坏,并呈现弹性性质,在弹性区内随着爆心距的增加介质内应力衰减速度趋近于0,介质内部的应力也趋近于0。

图2 不同破坏区域中的径向应力分布Fig.2 Radial stress distribution in different fracture zones

2.2 准静态爆腔与其他方法的对比

为了验证模型的准确性,在山东东营地区进行了球形装药的土中爆炸成腔实验,该实验中土壤的具体参数见表3。将土壤的具体参数代入亨利奇提出的动态模型[3]进行计算,将动态模型计算的结果、本文中提出的准静态模型以及土中爆炸空腔实验测得的数据进行对比,结果见图3～4和表4。从图中可以看出,动态爆腔能够展现出空腔随时间的变化情况,并最终趋近于某个终值,该终值就是动力学模型计算得出的爆腔终态尺寸。

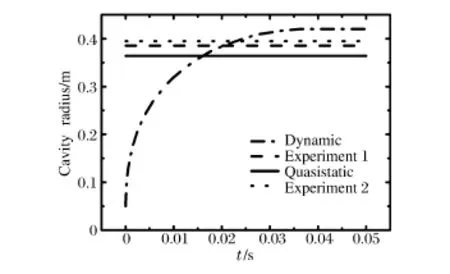
图3 1 k g炸药爆炸产生空腔尺寸Fig.3 Radius of cavity created by 1 kg TNT

图4 2 k g炸药爆炸产生空腔尺寸Fig.4 Radius of cavity created by 2 kg TNT

表3 测试现场土壤参数Table 3 Parameters of soil in testing field

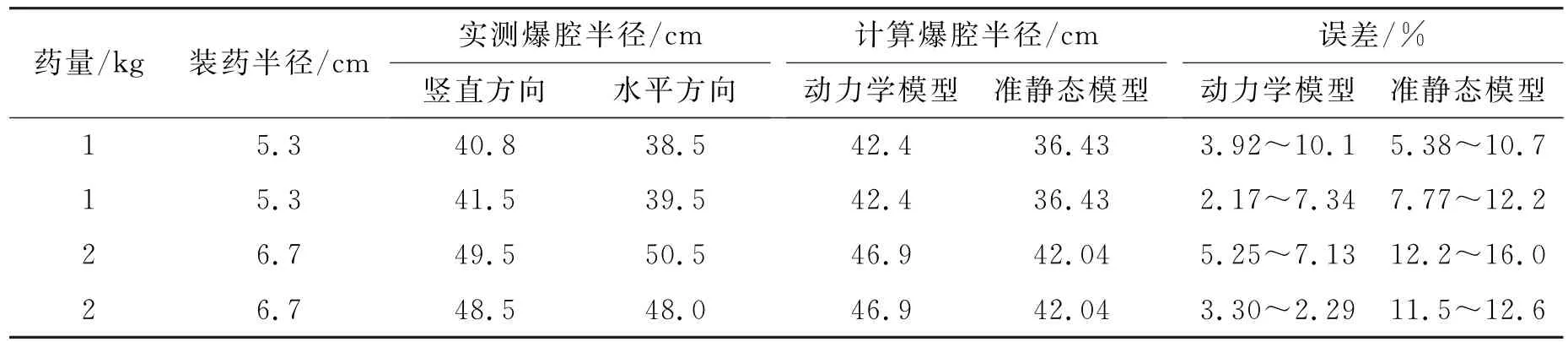
表4 爆炸成腔现场测试与计算结果对比Table 4 Comparison of the cavity between tests and calculations

通过对比分析实验值与计算值的结果可以得出:准静态模型与实测数据的误差约在5.4%～16. 0%之间,表明该方法能够比较准确地预测爆腔特征尺寸;误差产生的原因主要包括两点:(1)炸药在不饱和土中爆炸后,产生的空腔壁上会产生一些裂隙,爆生气体的楔入效应会使空腔进一步膨胀,而忽略这种气体的楔入对爆腔尺寸的影响往往会导致计算结果比实际结果偏小;(2)当地震波传播到自由面时会发生波的反射,反射波对介质的拉伸也会进一步扩大爆腔尺寸。

与准静态理论相比,虽然动态模型得到的空腔尺寸与实验值的误差较小,但是由于准静态模型计算简便,耗费时间短,因此更适合应用于实际工程中。

3 结 论

为了准确预测球形装药产生爆腔的特征尺寸,本文中基于爆炸前后的平衡条件建立了一种球形装药条件下的准静态空腔模型。通过参数分析与实验对比得出了以下结论:

(1)模型中分别给出了炸药土中爆炸所产生的空腔、粉碎区、裂隙区半径的解析表达式,且表达式中的参数获取相对简单;

(2)将准静态模型与试验得到结果进行对比,误差在5%～16%之间;这主要是由于爆生气体楔入爆腔表面裂隙,以及反射波对岩土介质的拉伸所导致的,在后续工作中分别对这两部分内容进行考虑可以进一步提高该模型的准确性。

(3)与动力学模型相比,准静态模型计算简便、耗时短,更适用于实际工程计算。

[1] Favreau R F.Generation of strain waves in rock by an explosion in a spherical cavity[J].Journal of Geophysical Research,1969,74(17):4267-4280.

[2] 亨利奇J.爆炸动力学及其应用[M].熊建国,译.北京:科学出版社,1987:239-252.

[3] Holmberg R,Persson P A.The Swedish approach to contour blasting[C]∥Proceedings of the 4th Conference on Explosives and Blasting Technique.New Orleans,LA:ISEE,1978:113-127.

[4] Ouchterlony F.Prediction of crack lengths in rock after cautious blasting with zero inter-hole delay[J].Fragblast, 1997,1(4):417-444.

[5] Ouchterlony F,Olsson M,Bergqvist I.Towards new Swedish recommendations for cautious perimeter blasting [J].Fragblast,2002,6(2):235-261.

[6] Kanchibolta S S,Valery W,Morrell S.Modeling fines in blast fragmentation and its impact on crushing and grind-ing[C]∥The Australasian Institute of Mining and Metallurgy Proceeding of Explosion 99-A Conference on Rock Breaking.Australia:Brisbane,1999:137-144.

[7] Chernikov A,Sher E.A quasistatic model of a confined explosion of a concentrated charge in a bed and in a block [J].Journal of Mining Science,1990,26(4):355-362.

[8] Forrestal M J,Tzou D Y.A Spherical cavity-expansion penetration model for concrete targets[J].International Journal of Solids and Structures,1997,34(31):4127-4146.

[9] Voitenko Y I.Fracture of solids by weak blasts[J].Combustion,Explosion,and Shock Waves,1995,31(4):492-496.

[10] Drukovanyi M F,Kravtov V S,Chernyavskii Y E,et al.Calculation of fracture zones created by exploding cylindrical charges in ledge rock[J].Soviet Mining Science,1976,12(3):292-295.

[11] Ding H,Zheng Z M.Source model of blasting vibration[J].Science in China,Series E,2002,45(4):395-407.

Quasi-static model for predicting explosion cavity with spherical charges

Yu Chenglong,Wang Zhongqi
(State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing100081,China)

The characteristic dimension of the explosion-generated cavity in the soil is the most important influence factor for the feature of the far field seismic wave.In this paper we established a quasistatic model to predict the characteristic dimension of the cavity.When a spherical charge was detonated in the homogeneous,incompressible,infinite and elastic mediums,the analytical expressions of the fine crushing zone and the radial fissures zone were shown in this model.In addition,we also used this model to calculate the dimension of the divisions in different conditions.Finally,we conducted a comparison among the quasi-static model,the dynamic model and the experiments.The errors range of the quasi static model was 5.4%-16.0%.The results show that our model can be used to predict exactly the dimension of the cavity.

spherical cavity;theory of quasi-static;fine crushing zone;radial fissures zone

O382国标学科代码:13035

:A

10.11883/1001-1455(2017)02-0249-06

(责任编辑 王小飞)

2015-07-21;

:2016-01-15

国家科技重大专项(2016ZX05006-002)

于成龙(1988- ),男,博士研究生,3120130145@bit.edu.cn。