爆破扰动下邻近层状围岩隧道的稳定性与振速阈值*

吴 亮李 凤卢文波陈 明许 锋

(1.武汉科技大学理学院,湖北武汉430065; 2.中铁港航-武汉科技大学爆破技术研究中心,湖北武汉430065; 3.武汉大学水资源与水电工程科学国家重点实验室,湖北武汉430072; 4.贵州新联爆破工程集团有限公司,贵州贵阳550002)

爆破扰动下邻近层状围岩隧道的稳定性与振速阈值*

吴 亮1,2,李 凤1,2,4,卢文波3,陈 明3,许 锋1,2

(1.武汉科技大学理学院,湖北武汉430065; 2.中铁港航-武汉科技大学爆破技术研究中心,湖北武汉430065; 3.武汉大学水资源与水电工程科学国家重点实验室,湖北武汉430072; 4.贵州新联爆破工程集团有限公司,贵州贵阳550002)

爆炸荷载下邻近既有层状围岩隧道的迎爆侧易发生开裂、破坏,确保既有隧道围岩在爆破扰动下的安全是隧道近接施工中的关键问题。基于弹性力学和结构力学原理,建立了既有层状围岩隧道迎爆侧最危险点的简化力学模型,得到了最危险点的应力计算表达式,分析了隧道半径与岩层厚度的比值、岩层的倾角、岩层所对应的圆心角和隧道埋深等因素对既有隧道围岩稳定性的影响规律,并依据岩体最大拉应力判据确定了既有层状隧道围岩稳定的质点临界振动速度,结合地震波传播时的衰减规律,可以得出爆破施工时的最大单响药量,从而为隧道近接爆破动力扰动施工提供理论依据。

围岩稳定;爆破;隧道;层状围岩;振动速度

随着我国国民经济的迅速发展,大量的铁路单线需要修建复线,如建设中的宝成复线、株六复线等。复线隧道施工爆破时产生的振动对既有隧道的影响一般都比较大,特别是对于复杂地质(如层状地质)的情况,有可能使邻近既有隧道损伤甚至坍塌。另外,地下开采、公路隧道以及水电站硐室群等工程都涉及到爆破对既有层状隧道扰动的问题。自然界中具有层状结构的沉积岩占陆地面积的三分之二,许多变质岩也具有层状构造特征,因而层状岩体是地下工程中经常遇到的一种岩体,研究复杂地质条件下既有隧道围岩损伤破坏的影响因素意义重大。

长期以来,隧道围岩稳定性判定没有科学合理的方法,常以洞周位移或塑性区经验值作为稳定判定指标[1]。由于洞周位移与隧道的振动存在一定的联系,故现实工程中一般通过监测洞周壁的振动速度监控隧道围岩的稳定性。许多学者对邻近均质隧道围岩的稳定性开展了研究,胡文清等[2]最早将有限元强度折减法引入隧道围岩稳定性分析中,并对木寨岭隧道进行了分析;文献[3-7]中对均质隧道进行了系统研究,提出了隧道的破坏机理及剪切安全系数和抗拉安全系数,并建立了相应的计算方法。边克信[8]建议采用一维应力波理论,根据岩石抗拉强度或岩石拉伸极限应变推算临界振动速度;朱瑞赓等[9]提出以岩体动力强度与隧洞所受动、静应力之和相平衡来确定爆破振动影响下无衬砌隧洞出现不同破坏时隧洞围岩临界振动速度的计算方法;P.K.Singh[10]对爆破冲击荷载作用下临近煤矿巷道的动力损伤问题进行了数值分析;J.Torano等[11]综合考虑了不同介质、装药量、起爆顺序等因素,通过建立三维有限元模型研究了隧道爆破振动速度的分布规律;刘国华等[12]基于加权双剪强度准则,提出了邻近爆破的安全评估方法。另外,国内学者对近距离爆破下隧道周边振动场分布规律也进行了大量的研究[13-19],分析了不同爆心距、地质条件、间距、布置方位等情况下既有隧道围岩与衬砌的响应规律。

目前,国内外学者已经对新建隧道爆破扰动下既有隧道的围岩稳定性进行了大量的分析,但是定量的理论研究相对而言还比较少。本文中,基于弹性力学和结构力学原理建立既有层状围岩隧道迎爆侧的简化模型,研究新建隧道爆破扰动下既有层状围岩隧道的稳定性影响因素及变化规律,得出既有层状围岩隧道的临界振动速度,以期为工程施工提供理论依据。

1 计算模型及过程

1.1 计算模型及假设

在层状地质条件下邻近隧道开挖过程中,爆破扰动可能会引起邻近既有层状围岩隧道的振动,继而危及既有隧道的安全,特别是既有隧道迎爆侧的安全。隧道层状围岩受力情况如图1所示,其中岩层与水平方向的夹角为θ,与隧道相交部分在隧道中可见长度为2L,对应的圆周角为δ,岩层厚度为h,隧道半径为R,邻近隧道洞壁的层状围岩受到覆盖围岩的重力为G2,层状岩体自重为G1,邻近隧道爆破开挖而产生的爆破扰动荷载为Fd。

根据层状围岩的实际受力及位移情况,对其作如下假设:(1)该层状围岩可以等效为两端固定的梁;(2)岩体为均质各向同性材质;(3)梁的破坏形式为拉伸破坏;(4)爆破荷载以水平入射;(5)梁的重力均匀分布在梁上,为常体力,作用于梁上的力可分解为平行于梁的力和垂直于梁的力。

1.2 计算过程

梁(层状围岩)的受力情况如图2和图3所示,其中x、y分别为平行于梁和垂直于梁的方向;σd和τd分别为爆破荷载与层状岩体上覆盖围岩重力的合力作用于梁垂直方向的正应力和平行方向的切应力;fx和fy为梁自重在x、y方向上的分力,即

图1 隧道层状围岩受力示意图Fig.1 Force diagram of layered rock surrounding the tunnel

图2 梁的受力情况Fig.2 Stress analysis of beam

图3 解除右侧约束后梁的受力Fig.3 Stress after removing constraint of right side

由图2可知,当梁仅受水平分力作用时,运用半逆解法[20]可假设梁沿y方向的应力为:

引入应力函数Φ,有:

式中:σx为梁沿x方向的应力,τxy为沿y轴方向作用于梁x面上的切应力。将式(1)代入式(2)得:

式中:f1(y)和f2(y)表示任意关于y的一次函数。将式(3)代入相容方程得:

由于式(4)对于任意的x都成立,故解得:

式中:A1、B1、C1、D1和E1为常数。将其代入式(2)得:

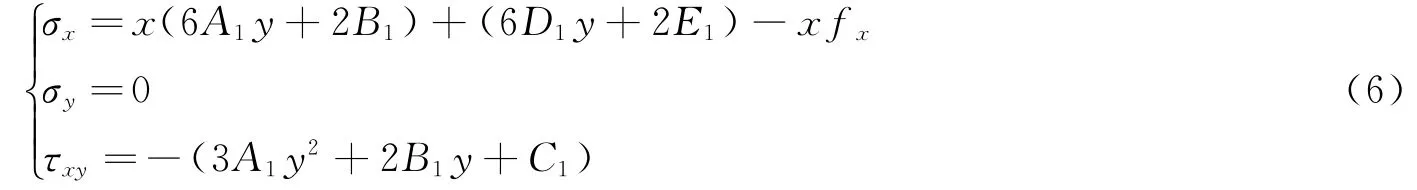
将结构一端的约束解除代之以相应的力,得如图3所示的结构受力。

根据力法原理[21]解得:

式中:FN为拉力,FS为剪切力,M为力矩。引入边界条件:解得:

当梁仅受垂直方向的力时,则由图2中梁的受力情况可知:

重复上述方法,引入应力函数后求解得到:

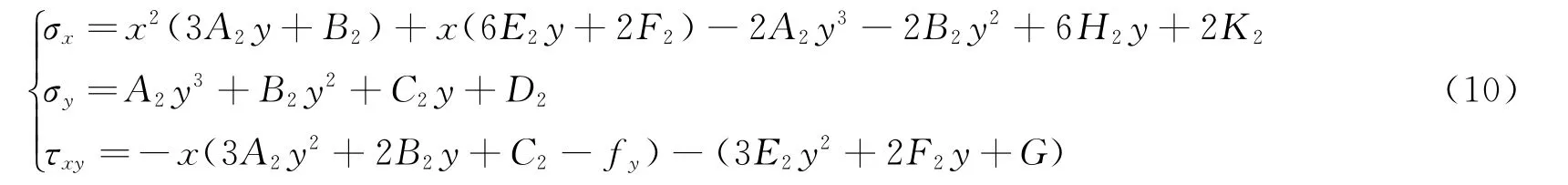
式中:A2、B2、C2、D2、E2、F2、G、H2和K2为常数。同理,将结构一端的约束解除代之以相应的力,得到梁的受力情况如图3所示。

利用力法原理解得:

因为yz平面是梁和荷载的对称面,所以应力分布应当对称于yz面;σx和σy是x的偶函数,τxy是x的奇函数,综合以上条件可知:E2=F2=G=0。引入边界条件:(σy)y=h/2=-σd,(σy)y=-h/2=0,解得:

综上所述,梁的中间截面上最危险点x方向拉应力的表达式为:

利用图1中参数可以将σd、τd、fx、fy表示如下:σd=Fdsinθ+G2cosθ;τd=G2sinθ-Fdcosθ;fx=ρgsinθ;fy=ρgcosθ;G2=ρgH,其中ρ为岩体密度,H为隧道埋深。另外,层状岩层与隧道边界相交的两点间的圆弧对应的圆心角为δ,故L=Rsin(δ/2)。将以上表达式代入式(13)可得:

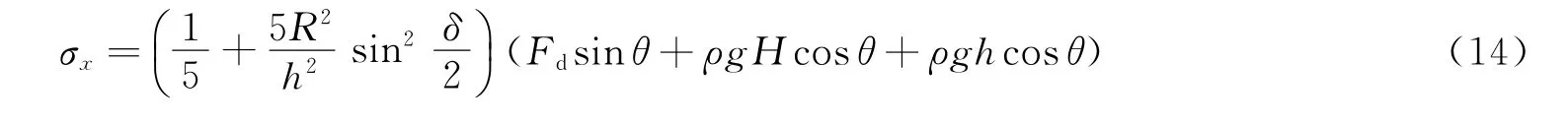
2 计算结果分析

爆破扰动载荷Fd=ρcv,其中ρ=2.3 g/cm3,纵波波速c=3.6 km/s,v为爆破振动速度。运用控制变量法,除以某参数作为变量的情况外,各参数取值为:δ=10°,H=20 m,R=3 m,h=0.4 m,θ=45°。将数据代入式(14),通过计算得出,不同爆破振动速度下岩梁正应力(σx)随各影响因素的变化规律如图4～图9所示。需要说明的是,计算过程中直接取覆盖层重力作为岩层的覆盖压力。由于实际施工中岩层存在应力扩散作用,本文计算所得结果偏大,如需精确计算,应结合地应力的实测数据。

图4为不同爆破质点振速条件下岩层厚度与岩梁正应力(σx)的关系曲线。图4显示:σx随着岩层厚度的增大而减小,两者近似呈反比例关系。当隧道围岩仅受静力作用(v=0 cm/s)时,σx的变化规律与文献[22]中武当山层状隧道监测得出的结论一致,表明本计算模型是合理的。随着爆破质点振速的增加,岩体应力也不断增大;但随着岩层厚度的增加,σx的增幅逐渐减小。

图5为岩层倾角与岩梁正应力的关系曲线。当岩层仅受静力作用时,σx随着岩层倾角的增加而减小,并且均小于1 MPa,因此既有层状隧道在不受爆破扰动时是稳定的。当有爆破扰动时,σx随岩层倾角的增加而增加,但增加速率逐渐减小,在85°时达到最大值;σx的增长速率随着爆破扰动的增加而逐渐增加;当岩层处于水平时,爆破动力扰动对岩梁正应力没有贡献,此时岩梁正应力主要是由静压力引起的。由于爆破动扰动易使岩层沿结构面因发生相互错动而破坏,故新建隧道施工产生的爆破扰动易使既有层状围岩隧道的迎爆侧岩体发生节理面间的剪切破坏。

图4 岩层厚度与岩梁正应力关系曲线Fig.4 Stress vs.the thickness of rock layer

图5 岩层倾角与岩梁正应力关系曲线Fig.5 Stress vs.the angle of rock layer

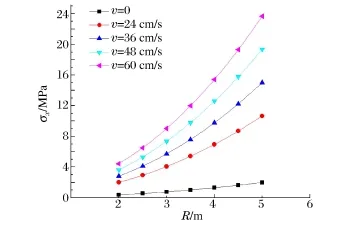
图6 隧道半径与岩梁正应力关系曲线Fig.6 Stress vs.tunnel radius

图7 覆盖层厚度与岩梁正应力关系曲线Fig.7 Stress vs.the thickness of covering layer

图6为隧道半径与岩梁正应力的关系曲线。当围岩仅受静力作用时,σx随着隧道半径的增加而增加,但是增长较慢,其值较小。当有爆破扰动时,σx与隧道半径成正比,且增幅速率呈逐渐增加趋势;σx的增长速率与爆破扰动强度成正比,这是因为当隧道半径增加时,梁的长度增加,其刚度减小,故围岩质点的动应力增大。图7为覆盖层厚度(H)与岩梁正应力关系曲线。由图7可知:σx随着覆盖层厚度的增大而增大,且基本呈现线性关系,其斜率与爆破扰动无关,因此,当既有隧道仅受静力作用且埋深达到一定深度时,要注意隧道的安全支护。

图8为层状围岩所对应夹角与应力关系曲线。由图8可知:σx及其增幅均随着层状围岩所对应夹角的增大而增大,且爆破扰动下其增幅更加明显。图9为隧道半径和层状厚度比与岩梁正应力关系曲线。图9显示:σx随着半径与厚度之比的增加而增加,且呈幂指数规律变化;层状围岩所对应夹角越大,σx的增长速率越大;并且R/h与δ乘积相等时,σx取值相同。

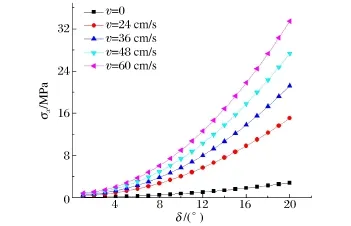
图8 层状围岩所对应夹角与应力关系曲线Fig.8 Stress vs.the corresponding angle of rock layer

图9 隧道半径和层状厚度比与岩梁正应力关系曲线Fig.9 Stress vs.the ratio of tunnel radius to thickness

3 安全振速

根据最大主拉应力理论判据,为了使隧道周壁不出现裂纹,则

式中:[σ]t为最大安全应力。由式(15)可得,爆破施工时,邻近层状隧道最危险点出现裂纹的临界爆破振动速度(即最危险点所能承受的最大爆破质点振动速度)为

由式(16)可知,当埋深及层状的倾角一定时,R/h与δ乘积越大,最大振动速度越小。根据既有隧道的半径和埋深、层状围岩的厚度、层状围岩相对隧道的位置等可以计算得到既有隧道的安全质点振动峰值速度;再结合爆破质点振动衰减公式,即可确定出爆破施工时的最大单响药量。

4 结 论

基于弹性力学和结构力学原理,建立了既有层状围岩隧道迎爆侧最危险点的简化力学模型,得到了最危险点的应力计算表达式,分析了各相关因素对既有隧道围岩稳定性的影响规律,得到以下结论。

(1)σx随着爆破质点振速的增加而增大;但是随着岩层厚度的增加,σx的增幅逐渐减小。

(2)σx随着层状倾角的增大而增大,且增大速率逐渐减小,在85°时达到最大值;σx增长速率随着爆破扰动的增大而逐渐增大,当岩层处于水平时,σx主要是由静压力引起,爆破扰动没有贡献。

(3)σx及其增幅均随着隧道半径的增大而增大,并且σx的增幅与爆破扰动强度成正比。

(4)σx随着覆盖层厚度的增大而增大,两者基本呈线性关系,其比例系数与爆破扰动无关。

(5)σx及其增幅均随着层状围岩所对应夹角的增大而增大,且爆破扰动下其增幅更加明显。

(6)σx随着半径与厚度之比的增大而增大,且两者呈幂指数关系。

(7)利用计算所得最危险点最大振速的计算公式,结合爆破质点振动衰减公式,可以确定出爆破施工时的最大单响药量。

参考文献:

[1] 张志强,何本国,关宝树.节理岩体隧道围岩稳定性判定指标合理性研究[J].现代隧道技术,2012,49(1):12-19. Zhang Zhiqiang,He Benguo,Guan Baoshu.A study of the criterion for the stability of a tunnel in a jointed rock mass[J].Modern Tunnelling Technology,2012,49(1):12-19.

[2] 胡文清,郑颖人,钟昌云.木寨岭隧道软弱围岩段施工方法及数值分析[J].地下空间,2004,24(2):194-197. Hu Wenqing,Zheng Yingren,Zhong Changyun.Construction method and numerical analysis on Muzhailing tunnel [J].Underground Space,2004,24(2):194-197.

[3] 张黎明,郑颖人,王在泉,等.有限元强度折减法在公路隧道中的应用探讨[J].岩土力学,2007,28(1):97-101. Zhang Liming,Zheng Yingren,Wang Zaiquan,et al.Application of strength reduction finite element method to road tunnels[J].Rock and Soild Mechanics,2007,28(1):97-101.

[4] 郑颖人,赵尚毅,邓楚键,等.有限元极限分析法发展及其在岩土工程中的应用[J].中国工程科学,2006,8(12):39-61. Zheng Yingren,Zhao Shangyi,Deng Chujian,et al.Development of finite element limit analysis method and its application to geotechnical engineering[J].Engineering Science,2006,8(12):39-61.

[5] 郑颖人,邱陈瑜,张红,等.关于土体隧洞围岩稳定性分析方法的探索[J].岩石力学与工程学报,2008,27(10):1968-1980. Zheng Yingren,Qiu Chenyu,Zhang Hong,et al.Exploration of stability analysis methods for surrounding rocks of soil tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(10):1968-1980.

[6] 郑颖人,邱陈瑜,宋雅坤,等.土质隧洞围岩稳定性分析与设计计算方法探讨[J].后勤工程学院学报,2009,25(3): 1-9. Zheng Yingren,Qiu Chenyu,Song Yakun,et al.Exploration of stability analysia and design calculation methods of surrounding rocks in soil tunnel[J].Journal of Logistical Engineering University,2009,25(10):1-9.

[7] 郑颖人,徐浩,王成,等.隧洞破坏机理及深浅埋分界标准[J].浙江大学学报,2010,44(10):1851-1856. Zheng Yingren,Xu Hao,Wang Cheng,et al.Research on the failure mechanism of tunnel and dividing line standard between shallow and deep bury[J].Journal of Zhejiang University,2010,44(10):1851-1856.

[8] 边克信.爆破地震对地下构筑物的影响[J].中国矿山工程,1981,1(6):25-36. Bian Kexin.Influence of blasting seismic on underground structure[J].China Mine Engineering,1981,1(6):25-36.

[9] 朱瑞赓,李铮.爆炸地震波的现场测量及其安全距离[J].爆炸与冲击,1982,2(1):60-67. Zhu Ruigeng,Li Zheng.In-situmeasurements of blasting seismic waves and their safety distance[J].Explosion and Shock Waves,1982,2(1):60-67.

[10] Singh P K.Blast vibration damage to underground coal mines from adjacent open-pit blasting[J].International Journal of Rock Mechanics and Mining Sciences,2002,39(8):959-973.

[11] Torano J,Rodríguez R,Diego I,et al.FEM models including randomness and its application to the blasting vibrations prediction[J].Computers and Geotechnics,2006,33(1):15-28.

[12] 刘国华,王振宇.爆破荷载作用下隧道的动态响应与抗爆分析[J].浙江大学学报,2004,38(2):204-209. Liu Guohua,Wang Zhenyu.Dynamic response and blast-resistance analysis of a tunnel subjected to blast loading [J].Journal of Zhejiang University,2004,38(2):204-209.

[13] 阳生权.小线间距施工隧道爆破地震影响下既有隧道围岩线性动力分析[J].工程爆破,1998,4(1):1-6. Yang Shengquan.Linear dynamic analysis on rock-media of old tunnel affected by blasting vibration of new tunnel with small line-clearance[J].Engineering Blasting,1998,4(1):1-6.

[14] 张庆松,李利平,李术才,等.小间距隧道爆破动力特性试验研究[J].岩土力学,2008,29(10):2655-2660. Zhang Qingsong,Li Liping,Li Shucai,et al.Experimental study of blasting dynamic vibration of closely adjacent tunnel[J].Rock and Soild Mechanics,2008,29(10):2655-2660.

[15] 王明年,潘晓马,张成满,等.邻近隧道爆破振动响应研究[J].岩土力学,2004,25(3):412-414. Wang Mingnian,Pan Xiaoma,Zhang Chengmam,et al.Study of blasting vibration influence on close-spaced tunnel[J].Rock and Soild Mechanics,2004,25(3):412-414.

[16] 毕继红,钟建辉.邻近隧道爆破震动对既有隧道影响的研究[J].工程爆破,2004,10(4):69-73. Bi Jihong,Zhong Jianhui.Study on influence of blasting vibration from excavation of a new tunnel on existed tunnel[J].Engineering Blasting,2004,10(4):69-73.

[17] 吴亮,钟冬望.不同布置条件下邻近隧道掘进爆破对既有隧道的影响[J].煤炭学报,2009,34(10):1339-1343. Wu Liang,Zhong Dongwang.Effect of tunneling blasting on the existing adjacent tunnel under different conditions [J].Journal of China Coal Society,2009,34(10):1339-1343.

[18] 王新宇,邵珠山,乔汝佳.小净距下穿铁路隧道爆破震动的响应研究[J].应用力学学报,2013,30(4):527-532. Wang Xinyu,Shao Zhushan,Qiao Rujia.Study on the dynamic responses of blasting vibration on undercrossing railway tunnel with small distance[J].Chinese Journal of Applied Mechanics,2013,30(4):527-532.

[19] 苏永贵,赵跃堂.爆炸长波作用拱形坑道在不同侧压力系数下的应力与破坏分析[J].国防交通工程与技术,2015, 13(1):50-53. Su Yonggui,Zhao Yuetang.A stress-and-failure analysis of an arched tunnel under the action of the long-wave explosion with different lateral-pressure coefficients[J].Traffic Engineering and Technology for National Defence, 2015,13(1):50-53.

[20] 徐芝纶.弹性力学[M].北京:高等教育出版社,2006:41-45.

[21] 李廉锟.结构力学[M].北京:高等教育出版社,2004:130-132.

[22] 徐颖,陈建平,左昌群.武当群片岩隧道剪切型纵向裂缝破坏机理[J].中南大学学报(自然科学版),2013,44(7): 2950-2957. Xu Ying,Chen Jianpping,Zuo Cangqun.Shear type longitudinal cracks failure mechanism in Wudang group of schist tunnel[J].Journal of Central South University(Science Edition),2013,44(7):2950-2957.

Vibration velocity threshold of a tunnel adjacent to surrounding layered rocks under blasting load

Wu Liang1,2,Li Feng1,2,4,Lu Wenbo3,Chen Ming3,Xu Feng1,2
(1.College of Science,Wuhan University of Science and Technology,Wuhan430065,Hubei,China; 2.Blasting Technology Research Center,CRPCE-WUST,Wuhan430065,Hubei,China; 3.State Key Laboratory of Water Resource and Hydropower Engineering Science,Wuhan University,Wuhan430072,Hubei,China; 4.Guizhou Xinlian Blasting Engineering Group Co Ltd,Guiyang550002,Guizhou,China)

Under a blasting load,the front side adjacent to blasting in an existing tunnel surrounded by layered rocks is apt to be destroyed,and therefore it is of critical importance to keep the tunnel safe from the destructive effects of the surrounding rocks’cracks and damages that occur in a blasting disturbance.In this work,based on elastic mechanics and structural mechanics,we established a simplified mechanical model for the most dangerous point of the tunnel’s blasting side,and obtained the stress formula that can calculate the stress at this point.We also analyzed the regular influence of such different factors as the ratio of the tunnel radius to the thickness of layer,the inclination angle, the central angle and depth of the surrounding layered rocks on the stress.In addition,using the theory of the maximum tensile stress,we calculated the surrounding rocks’critical vibration velocity that ensures the stability of the tunnel and obtained,according to the attenuation patterns of seismic wave propagation,the maximum charge of detonation for the construction of a new tunnel.

stability of surrounding rock;blasting;tunnel;layered rock;vibration velocity

O382.2国标学科代码:13015

:A

10.11883/1001-1455(2017)02-0208-07

(责任编辑 王玉锋)

2015-09-07;

:2015-11-18

国家自然科学基金项目(51004079;51479147);湖北省自然科学基金项目(2014CFB822);水利部科技推广计划项目(TG1522)

吴 亮(1980- ),男,博士,副教授,wuliangwust@sina.com。