多次激波诱导正弦扰动预混火焰界面失稳的数值研究*

陈 霄,董 刚,蒋 华,吴锦涛

(南京理工大学瞬态物理重点实验室,江苏南京210094)

多次激波诱导正弦扰动预混火焰界面失稳的数值研究*

陈 霄,董 刚,蒋 华,吴锦涛

(南京理工大学瞬态物理重点实验室,江苏南京210094)

激波诱导火焰失稳是实际中常见的现象,为深入研究火焰失稳特性,采用三维单步化学反应的Navier-Stokes方程和9阶weighted essentially non-oscillatory(WENO)的高精度格式,对不同马赫数的入射激波及其反射激波多次诱导正弦型预混火焰界面失稳的现象进行了三维数值模拟,并对计算结果的可靠性进行了验证。研究结果显示,在激波的多次作用下,火焰界面的演变过程主要受Richtmyer-Meshkov(RM)不稳定特性和化学反应特性的双重影响,且随着入射激波强度的增强,上述2种特性均得到进一步强化。为构造体现反应性RM不稳定特性的参数,根据火焰界面混合区平均涡量和化学反应速率,提出了表征界面受不稳定性和化学反应影响的量纲一参数。通过分析发现,在同一入射激波强度下,该参数的对数形式随入射激波和反射激波的多次作用呈基本相同的线性增长趋势;对不同马赫数的入射激波,该参数对数形式的线性增长率也基本一致。这样的变化表明该量纲一参数能够反映反应性RM不稳定过程中火焰界面发展的内在规律。

激波;火焰失稳;WENO;RM不稳定;化学反应

激波掠过火焰界面时,若压力梯度和密度梯度方向不一致,也就是激波与火焰界面的方向不一致,会形成斜压效应从而诱导界面产生Richtmyer-Meshkov(RM)不稳定,使火焰界面失稳变形,从而加快未燃气和可燃气的混合、强化燃烧速率。这一现象不仅出现在超行星爆炸[1]等自然现象中,还广泛表现在工业灾害[2]、发动机超燃混合[3]等过程中,因此对激波诱导的火焰失稳、燃烧和混合等特性的研究是具有重要实际意义的。

G.H.Markstein[4]首先对激波与火焰相互作用的过程进行了实验研究,并获得了火焰界面失稳形态的图像。V.T.Ton等[5]和Y.Ju等[6]对激波与球形火焰相互作用进行研究时发现,入射激波的强度对火焰界面变形有显著影响。当入射激波较弱时,火焰界面的变形基本与惰性界面的变形相似;当激波变强时,火焰界面会拉伸增长,增加未燃气与已燃气的接触范围,从而强化了燃烧过程。E.S.Oran等[2]在前人的研究基础上,开展了一系列平面激波与球形火焰相互作用的数值研究,详细讨论了激波作用下火焰变形和反应放热的规律,并探讨了火焰变形引发热点形成和爆轰产生的特点。朱跃进等[7-8]对平面入射激波及其反射激波诱导球形火焰失稳变形的现象进行了二维和三维数值模拟,通过定义的量化参数,分析了流场中失稳火焰的演变过程、火焰几何量变化、燃烧放热规律、混合与燃烧的作用关系等特性。

上述研究主要针对的是平面激波和球形火焰界面的相互作用,而其他火焰界面类型的研究并不多见。A.M.Khokhlov等[9]曾采用带化学反应的二维Navier-Stokes方程对入射激波与正弦型扰动的火焰界面的单次作用过程进行了数值研究,结果表明,火焰失稳变形的主要机制是RM不稳定,这种不稳定能强化已燃气与周围未燃气的混合,使燃烧速率和放热速率均有所提高,但在火焰受到单次激波作用的情况下,这种强化的程度是有限的。V.Kilchyk等[10]报道了单模扰动预混火焰界面在单次激波作用下的不稳定过程,着重考察了压缩波和稀疏波对界面处燃料消耗速率的影响,结果发现,对不同形态的界面,激波压缩与RM不稳定对燃料消耗与反应速率变化的影响程度是不同的。L.Massa等[11]研究激波单次作用下预混火焰界面的失稳机制过程中,发现火焰界面的扰动增长速度明显受到化学反应的影响,并且化学反应会减少火焰表面的小尺度扰动。但是,这类研究主要针对的是激波与带初始扰动的火焰界面的单次作用,而激波与火焰界面多次作用的研究尚未见报道。

受限空间内(如发动机燃烧室),激波与带初始扰动的火焰作用后经由壁面反射,很可能与火焰再次作用,多次作用的结果会使火焰界面的扰动发展与单次激波作用后的变化有明显不同。已有的激波与惰性界面多次作用的研究表明,入射激波作用后,惰性界面扰动增长依赖于初始界面扰动;而反射激波作用后的扰动增长则不依赖于初始界面扰动[12-13],其中,体现界面物理混合过程的混合区宽度(mixing zone,MZ)常被用来表征界面扰动的这种增长。而对反应性界面,加入了化学反应影响的多次激波作用下的扰动演变特性及其表征方法还值得进一步研究。因此,本文中基于二维带化学反应的Navier-Stokes方程,采用高精度计算格式,对入射激波及其反射激波与预混火焰正弦型扰动界面的多次作用过程进行二维数值研究。考察不同强度入射激波作用下,受RM不稳定和化学反应作用影响的界面失稳演化特性,确定表征火焰界面扰动发展的参数并进行分析。

1 数理模型和实验验证

1.1 数学模型和计算方法

为准确地描述激波与火焰的相互作用过程,采用了二维带化学反应的Navier-Stokes(NS)控制方程,表达式为

式中:ρ为密度;ui为i方向速度(i=1,2);p为总体系压力;τij为黏性应力张量;E为单位体积总能量,E为比热比,q为单位质量的总化学能,Y为反应物质量分数;qj为热通量,qj=-k∂T/∂xj;传导系数k、扩散系数D和τij中隐含的运动学黏度ν表达式为[2]

式中:ν0、D0、k0是常数,T为温度,假设Lewis、Prandtl和Schmidt数均为1,故可选取常数ν0=D0=k0=3.2×10-7kg/(s·m·K0.7)[8];v为化学反应速率,采用具有Arrhenius形式的单步反应形式:

式中:指前因子A和活化能Ea等化学动力学参数的选取参见文献[7]。

式(1)～(4)中,对流项采用9阶weighted essentially non-oscillatory(WENO)的高精度格式[14]进行计算,以精确捕捉火焰界面的不稳定精细结构;输运项采用10阶中心差分的格式进行求解;时间推进过程则采用3阶Runge-Kutta方法进行计算。

1.2 实验验证

为验证本文计算方法、网格尺寸和化学反应参数的可靠性,依据文献[15]的实验结果对入射激波与球形火焰的相互作用过程进行了数值模拟和实验验证。考虑到实验图像是三维可视化结果,因此数值计算采用了二维轴对称的含化学反应的NS方程和正交化的均匀网格,网格尺寸为Δx=Δy=0.1 mm。计算时,入射激波强度为Ma=1.7,初始球性火焰半径为19 mm,初始入射激波距球形火焰中心的距离为23 mm。球形火焰外部为C2H4+3O2+4N2预混气,初始压力和温度分别为p0=13.3 kPa和T0= 293 K,而火焰内部为该预混气在绝热等压燃烧条件下产生的已燃气体。预混气与已燃气的密度分别为ρ1=0.161 5 kg/m3和ρ2=0.015 78 kg/m3,由此得出,球形火焰界面初始的Atwood数为(ρ2-ρ1)/(ρ2 +ρ1)=-0.82。图1给出了入射激波与球形火焰相互作用后,火焰变形和流场波系结构的变化过程以及实验和计算结果的对比。流场采用阴影图像来显示,阴影图像的计算方法如下

式中:I代表亮度高低,系数I0取1.0。

图1 实验结果(上图)[15]与本文模拟结果(下图)对比Fig.1 Comparison of experimental results(upper pictures)[15]with computational results(lower pictures)

图1(a)为激波与球形火焰作用前的初始状态,计算和实验的初始条件严格吻合,具体可见文献[15]。图1(b)～(e)给出了间隔50μs的实验阴影照片和计算阴影图像的对比,可以看出,球形火焰变形形态和激波波系结构演化的数值模拟结果与实验结果吻合得很好,这说明本文的计算方法、化学反应参数以及所选取的网格尺寸是合理的和可靠的。

2 结果与讨论

2.1 计算的初始条件和边界条件

图2给出了入射激波(ISW)与正弦扰动火焰界面相互作用的初始状态以及计算区域的尺寸。初始界面为单模正弦扰动的预混火焰界面,扰动的初始振幅为a0=1.0 mm,初始波长λ0=20.0 mm。界面下部阴影部分为C2H4+3O2+4N2预混气,其初始压力和温度与1.2节相同(p0=13.3 k Pa和T0=293 K);界面上部是该预混气在绝热等压燃烧条件下的已燃气体。所以,已燃气与预混气的密度以及界面初始的Atwood数均与1.2节采用的数值相同。为考察不同入射激波强度对火焰界面作用的影响,本文中选取3种入射激波(Ma=1.2,1.7和2.2)进行数值模拟。表1为不同强度的激波入射条件下的计算条件,其中:l1、l2、l3如图2所示。入射激波初始位置位于火焰界面下方,与火焰界面中心的距离为l3,然后由下向上穿过界面。当透射激波到达计算区域上端壁面后发生反射,产生的反射激波由上向下运动再次与火焰界面发生作用,作用后一部分反射激波透过界面,还有一道新形成的激波由界面反射上行至壁面,然后反射后再下行与界面作用,这样的过程可以多次重复,导致多道反射激波不断与界面发生作用。为防止入射激波与火焰界面作用后产生的稀疏波走出计算区域下边界从而影响边界条件,对不同马赫数的计算沿y方向采用了不同长度的计算区域和入射激波初始位置,如图2与表1所示。

表1 计算区域尺寸Table 1 Size of computational domain

图2 二维计算模型Fig.2 2D numerical model

计算区域左右边界采用周期性边界条件,上边界为无滑移的刚性绝热壁面边界,下边界采用零梯度边界计算使用的均匀网格尺寸与1.2节中采用的相同(Δx=Δy=0.1 mm),此外,计算中CFL取0.5,满足时间推进的稳定性判据。3种马赫数条件下使用的网格数为1.0～1.2×106,计算量较大,为此,本文采用了基于CUDA(SDK 4.2/Toolkit 4.2)的GPU(Tesla C2075)并行计算架构来编制程序并完成上述计算。

2.2 火焰界面演变特性

由于入射激波强度和初始位置的不同,不同马赫数下界面演化的快慢是不一致的,因此本文中采用了特征时间(t0)对物理时刻进行量纲一化处理,以方便不同马赫数计算结果的比较:

式中:sISW代表入射激波的传播速度。

为考察不同入射激波强度对预混火焰界面不稳定发展的影响,图3给出了3种马赫数下火焰界面在4个典型时刻(t/t0=0.6, 0.9,1.1和1.6)的演化形态,这4个典型时刻分别代表入射激波、第1次反射激波、第2次反射激波和第3次反射激波作用后界面发展的某个瞬时。图3表明,初始正弦型扰动的火焰界面在激波作用下的典型失稳形态是所谓“钉(spike)”结构的形成和该结构沿流向(y方向)的发展,即密度较大的未燃气沿流向逐渐深入到密度较小的已燃气中。然而对不同的入射激波强度,钉结构在发展过程中表现出明显的不同。在Ma=1.2情况下(图3(a)),钉结构随着时间的发展沿流向持续拉长,由于斜压效应,在钉的顶部形成一个“钉帽”,但在后期由于化学反应的消耗,钉帽变小。此外,钉结构在发展过程中显示出明显的对称结构,钉的杆部的界面光滑平整。当入射激波Ma=1.7时(图3(b)),顶杆变得更加细长,且界面处出现明显波动并逐渐变得不对称(t/t0=1.1),到后期(t/t0=1.6)在化学反应的消耗作用下钉帽部分消失,顶杆沿流向也明显变短。当Ma= 2.2时(图3(c)),火焰界面的钉结构更加不稳定,在化学反应的作用下,钉的流向长度变得更短。

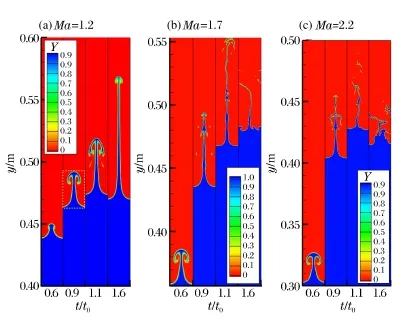
图3 不同时刻反应物浓度Fig.3 Distributions of reactant concentration at different times

为进一步考察火焰界面变化的原因,图4给出了Ma=2.2的情况下4个典型时刻其涡量幅值和化学反应放热率在流场中的分布,其中:灰度图像代表涡量ω,蓝色线条为化学反应放热率等值线,图4(a)、(b)、(c)、(d)中的等值线范围分别为3×1010～3×1011、3×1011～3×1012、3×1012～3×1013和3×1012～3×1013J/(m3·s)。由图4可以看出,化学反应放热率主要集中分布在火焰界面处(图3(c)),这表明化学反应主要是以预混火焰传播的机制起作用;而由RM不稳定导致的涡旋则主要分布在已燃气的区域,正是由于这些涡旋的作用,使得火焰界面拉伸变长,因而增加了火焰表面与未燃气的接触面从而逐渐强化了化学反应。入射激波作用后(图4(a)),由RM不稳定导致的涡量幅值较小,火焰界面的拉伸有限,因此反应放热率也较小。当一次反射激波自上而下作用后(图4(b)),再次的RM不稳定导致了新的涡旋出现,由于反射激波强度增加,其涡量幅值也显著增加,这就进一步强化了火焰界面的拉伸,使得化学反应放热率也显著增加。当第2次和第3次反射激波再次作用后(图4(c)～(d)),逐次发生的RM不稳定会导致涡旋的破碎及其数量的逐级增加[16],这种涡结构的不断精细化导致了钉结构出现不对称,尤其是在钉结构的顶部,涡旋运动促使已燃气和未燃气充分混合,使得钉结构的这一部分经化学反应消耗而完全消失(见图4(d))。

图4 不同时刻的涡量和化学反应放热率分布(Ma=2.2)Fig.4 Distributions of vorticity and heat release rate of chemical reaction at different times(Ma=2.2)

2.3 火焰界面演变的影响因素分析

2.2节的二维可视化结果分析表明,火焰界面的演变特性受到RM不稳定和化学反应特性的双重影响。为进一步定量分析上述2种特性对火焰界面的影响程度,图5给出了3种不同入射激波马赫数下,界面混合区内平均涡量幅值随时间的变化过程,平均涡量幅值表达为

式中:S为混合区单位网格,Sm代表界面混合区,定义为反应物平均质量分数在混合区上端为0.05%和下端为0.95%时所确定的流向长度与计算区域宽度所组成的矩形区域(见图3(a)中虚线框),反应物平均质量分数以x方向进行平均[17]:

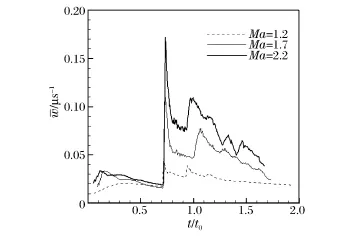
图5 平均涡量幅值随时间的变化Fig.5 Time histories of mean vorticity magnitude

图5的结果表明,第1次反射激波到达界面(t/t0=0.7)之前,3个马赫数下的平均涡量都较小;当更强的反射激波与界面作用时,由于斜压效应平均涡量骤升,作用之后由于黏性扩散涡量迅速下降;第2次反射激波到时(t/t0=0.9～1.1)平均涡量再次上升,峰值要比第一次反射波到达时小,然后随时间缓慢波动下降。尽管3个马赫数下的平均涡量变化规律类似,但马赫数越大,由斜压效应导致的平均涡量幅值也越大,因而对界面钉结构变化的影响也越大。另一方面,随着入射激波Ma数的增加,火焰界面处的化学反应将会进一步增强。

图6显示了3种不同强度入射激波条件下,界面混合区的平均化学反应速率随时间变化的规律,其中平均化学反应速率定义为

由图6可以看出,第1次反射激波到达界面(t/t0=0.7)之前,化学反应速率较小,当反射激波作用后,化学反应速率明显上升,随着后面几次反射激波的作用,化学反应速率仍持续上升。图6的结果还表明,马赫数越大,化学反应速率越快,即,马赫数越大,界面的形状受到化学反应影响的程度就越大。激波强度对界面化学反应的影响主要体现在2个方面:一是更强的激波波后气体有着更高的温度和密度,从而提供了更有利于化学反应进行的热力学环境;二是更强的激波导致了更高的涡量值(图5),使得已燃气/未燃气之间的混合更充分,因而也有利于化学反应的进行。

图5和图6的结果表明,涡量和化学反应速率的影响实际上可以归结为RM不稳定时间尺度(涡量)和化学反应时间尺度(反应速率)对火焰界面扰动发展的影响,因此可以定义一个量纲一参数η来表征反应性RM不稳定的演化过程,即

图6 平均化学反应速率随时间的变化Fig.6 Time histories of the mean rate of chemical reaction

图7给出了3种入射激波马赫数下η随时间的变化关系。在本文研究的时间范围内,3种马赫数下η值均小于1,这表明激波及其反射激波与预混火焰相互作用时,涡量引起的界面变化总是强于化学反应引起的界面变化。但是,除激波与界面正在作用的时段外(t/t0=0.7～0.8),化学反应对界面影响的程度是不断上升的,这意味着在界面演变的后期,化学反应的重要性正在逐渐增强。观察入射激波和反射激波作用后η的变化趋势发现,除激波正在作用时段外,η对数形式的上升速率基本一致。对上述3种马赫数下η的变化过程进行对数拟合,可以得到如下形式的表达式

式中:A1代表了对数形式的η随时间的增长率。对不同的入射激波马赫数,对数拟合的结果见表2,其中R2为可决系数。

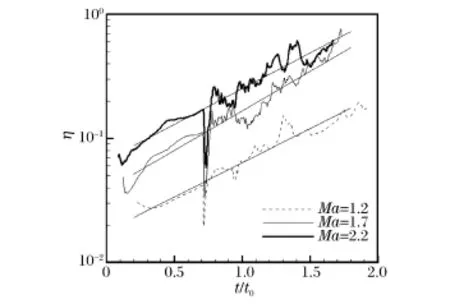
图7 η随时间的变化Fig.7 Time histories ofη

表2 η的拟合参数Table 2 Fitting perameters ofη

上述结果表明:一方面,在同一入射激波强度的条件下,lnη随时间呈线性增长趋势,且不随入射激波及其反射激波多次作用的影响;另一方面,对不同入射激波强度下,lnη的增长率亦基本相同。lnη对初始入射激波强度以及随后逐次激波作用的这种不依赖性(或弱依赖性)表明:lnη反映了激波作用火焰界面的过程中,RM不稳定导致的流动变化与化学反应导致的燃料消耗的相互竞争是控制界面扰动发展的主导因素,这种相互竞争并不显著依赖于激波强度或激波多次作用过程,因而可以视为表征反应性RM不稳定过程的一个特征参数。

3 结 论

采用高精度WENO格式,研究了激波与正弦型扰动预混火焰界面多次相互作用的过程,考察了激波强度大小对火焰界面形态的影响规律,得到如下结论:

(1)火焰界面的发展受化学反应和RM不稳定共同作用,由于入射激波与多次反射激波的连续作用,多次形成RM不稳定产生的涡旋运动不断拉伸火焰表面,使得界面两侧的未燃气和已燃气接触面积增加,因而强化了化学反应。

(2)提出了表征化学反应过程和RM不稳定过程竞争的量纲一参数,在研究的3种入射激波强度条件下,该参数的对数形式随时间呈线性增长趋势,表明化学反应对火焰界面扰动发展的影响逐渐增强。此外,该参数对数形式的增长率基本不随入射激波强度变化和激波多次作用而改变,表明该参数能够合理反映反应性RM不稳定过程发展的内在规律。

[1] Marble F E,Sonneborn G,Pun C S J,et al.Physic conditions in circumstellar gas surrounding SN 1987A 12 years after outburst[J].The Astrophysical Journal,2000,545:390-398.

[2] Oran E S,Gamezo V N.Origins of the deflagration-to-detonation transition in gas-phrase combustion[J].Combustion Flame,2007,148(1-2):4-47.

[3] Yang J,Kubota T,Zukoski E E.Applications of shock-induced mixing to supersonic combustion[J].AIAA Journal,1993,31(5):854-862.

[4] Markstein G H.A shock-tube study of flame front-pressure wave interaction[C]∥6th Symposium(International) on Combustion.Pittsburgh,USA:The Combustion Institute,1957:387-398.

[5] Ton V T,Karagozian A R,Marble F F,et al.Numerical simulations of high speed chemically reactive flow[J]. Theoretical and Computational Fluid Dynamics,1994,6:161-179.

[6] Ju Y,Shimano A,Inoue O.Vorticity generation and flame distortion induced by shock flame interaction[C]∥27th Symposium(International)on Combustion.Pittsburgh.USA:The Combustion Institute,1998:735-741.

[7] 朱跃进,董刚,刘怡昕,等.激波诱导火焰变形、混合和燃烧的数值研究[J].爆炸与冲击,2013,33(4):430-437. Zhu Yuejin,Dong Gang,Liu Yixin,et al.A numerical study on shock induced distortion,mixing and combustion of flame[J].Explosion and Shock Waves,2013,33(4):430-437.

[8] Zhu Yuejin,Dong Gang,Liu Yixin,et al.Three-dimensional numerical simulations of spherical flame evolutions in shock reshock accelerate flows[J].Combustion Science and Technology,2013,185(10):1415-1440.

[9] Khokhlov A M,Oran E S,Chtchelkanova A Y.Interaction of a shock with a sinusoidally perturbed flame[J]. Combustion and Flame,1999,117:99-116.

[10] Kilchyk V,Nalim R,Merkle C.Laminar premixed flame fuel consumption rate modulation by shocks and expansion waves[J].Combustion and Flame,2011,158:1140-1148.

[11] Massa L,Jha P.Linear analysis of the Richtmyer-Meshkov instability in shock-flame interactions[J].Physics of Fluids,2012,24:056101.

[12] Leinov E,Malamud G,Elbaz Y,et al.Experimental and numerical investigation of the Richtmyer-Meshkov instability under re-shock conditions[J].Fluid Mechanics,2009,626:449-475.

[13] Ukai S,Balakrishnan K,Menon S.Growth rate predictions of single-multi-mode Richtmyer-Meshkov instability with reshock[J].Shock Wave,2011,21:533-546.

[14] Balsara D S,Shu C W.Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy[J].Journal of Computational Physics,2000,160:405-452.

[15] Thomas G O,Bambrey R,Brown C.Experimental observations of flame acceleration and transition to detonationfollowing shock-flame interaction[J].Combustion Theory and Modelling,2001,5(4):573-594.

[16] 蒋华,董刚,陈霄,小扰动界面形态对RM不稳定性影响的数值分析[J].力学学报,2014,46(4):544-552. Jiang Hua,Dong Gang,Chen Xiao.Numerrical study on the effects of small amplitude initial perturbations on RM instability[J].Chinese Jounal of Theoretical and Applied Mechanics,2014,46(4):544-552.

[17] Latini M,Schilling O,Don W S.Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer-Meshkov instability[J].Journal of Computational Physics,2007,221:805-836.

Numerical studies of sinusoidally premixed flame interface instability induced by multiple shock waves

Chen Xiao,Dong Gang,Jiang Hua,Wu Jintao
(Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing210094,Jiangsu,China)

In this work,to further study the features of the shock-wave induced flame instability,the two-dimensional Navier-Stokes(NS)equations with the single-step chemical reaction and the high resolution 9th-order weighted essentially non-oscillatory(WENO)scheme were adopted to simulate the instability of the sinusoidally premixed flame induced by incident shock waves with different Mach numbers and its reshock waves.The computational results were validated by the experimental results in the related literature.The computational results show that the evolutions of the flame are mainly influenced by both the Richtmyer-Meshkov(RM)instability and the chemical reaction.With the growth of the incident shock wave intensity,the interface instability and the chemical reaction are enhanced.To construct the parameter that can characterize the RM instability in the reactive flow,a dimensionless parameter 8338A131 that describes the interface RM instability and the chemical reactivity was proposed based on the average vorticity and the chemical reaction rate calculated in the mixing zone of the flame interface.The analysis of the parameter shows that,with the similar intensity of the incident shock wave,the logarithmic form of the parameter exhibits basically the same linear growth when an incident shock wave with a given Mach number and its reshocks successively pass through the flame interface.The linear growth rate of the logarithmic form of the parameter is also basically the same for different Mach numbers of the incident wave.Such variations ofηsuggest that the dimensionless parameter proposed in the present study can well characterize the intrinsic features of the flame interface development in the reactive RM instability process.

shock wave;flame instability;WENO;Richtmyer-Meshkov instability;chemical reaction

O381国标学科代码:13035

:A

10.11883/1001-1455(2017)02-0229-08

(责任编辑 王小飞)

2015-07-20;

:2015-11-20

国家自然科学基金项目(11372140)

陈 霄(1990- ),女,博士研究生;

:董 刚,dgvehicle@yahoo.com。