基于PID和LQR算法的倒立摆控制设计

程明贺，陈仓

（长安大学，陕西 西安 710064）

专题 汽车设计与研究

基于PID和LQR算法的倒立摆控制设计

程明贺，陈仓

（长安大学，陕西 西安 710064）

文章建立了一级倒立摆的数学模型，并在此基础上通过MATLAB仿真工具对一级倒立摆的PID（Proportion Integration Differentiation）及LQR（Linear Quadratic Regulator）控制算法进行了设计与仿真。一般而言LQR控制算法的控制性能要优于PID控制算法。

倒立摆；PID；LQR

10.16638/j.cnki.1671-7988.2017.05.001

CLC NO.: U462.1 Document Code: A Article ID: 1671-7988 (2017)05-01-04

1、引言

倒立摆是一种典型的快速多变量非线性绝对不稳定非最小相位系统。这种控制的方法在航空航天、机器人等领域中都有着广泛的应用。从控制这个角度上讲，对倒立摆的研究在理论和方法上均有着深远的意义。同时由于倒立摆结构简单成本低廉因此成为人们学习研究和验证各种控制理论的理想装置。

2、一级倒立摆数学建模

直线倒立摆系统是一个机电一体化系统，由小车和摆杆组成。通过同步传送带驱动的[2]小车可以在水平方向的导轨上来回移动，位移的大小由固定在导轨的一端的位置传感器来测量，电机也固定在同一侧。摆杆通过转动铰链与小车相连，共轴角度传感器安装在小车和摆杆的连接处，用来测量摆杆转过的角度。在导轨的两端装有控制小车移动距离的开关，当小车到达左右两端附近的位置时，能够防止小车脱离导轨起到保护作用。

图1 一级倒立摆小车摆杆位置图以及受力隔离图

为了在数学上推导和处理问题的方便，可作出如下假设：

（1）摆杆在运动中是不变形的刚体；

（2）齿型带与轮之间没有相对滑动，齿型带长度保持不变；

（3）小车在移动的过程中，摩擦系数保持不变；

（4）忽略空气阻力；

基于上述条件假设，可将小车和匀质杆组成的系统模拟代替直线一级倒立摆系统（图1）。

图2 摆杆受力分析图

在文中，建立倒立摆的数学模型使用的方法是牛顿——欧拉法。小车和摆杆的相关参数如下所述：

x小车位移，单位(m)；β摆杆与垂直方向的夹角，单位(rad)；M小车的质量，单位(kg)；

m摆杆的质量，单位(kg)；l摆杆的转动轴心到摆杆质心的距离，单位m；J摆杆对重心的转动惯量，单位(kg·m2)；u电机对小车施加的作用力，单位(N)；F小车受到的等效摩擦力，单位(N)；

首先，对小车进行受力分析，如图1和图2所示。

其中，N和P表示小车与摆杆相互作用力的水平和垂直方向的分量。F为小车受到的作用力，x为小车位移，β为摆杆与垂直向上方向的夹角，θ为摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下)[3]。再结合例句平衡方程可以得到系统的运动方程：

注意：推导传递函数时假设初始条件为0。由于输出角度为Φ，求解方程组(9)得到传递函数为：

由于系统状态空间方程表达式为：方程组（5）对x˙˙，θ˙˙解代数方程，得到解如下：

式（6）为直线一级倒立摆系统在平衡点附近局部线性化以后得到的状态方程。将该式写成矩阵形式可以得到系统的状态空间方程为：

3、PID控制控制算法的设计

PID控制算法和模糊控制、神经网络控制等相比是一个非常传统的控制方式。PID控制的优点是应用范围比较广，而且参数较易调整。虽然倒立摆模型是非线性的，但通过对其简化可以变成基本线性的系统。

(1) 比例调节P

比例系数KP的大小决定了比例调节器调节速度的快慢，但KP过大会使控制系统出现超调或振荡现象，KP过小又起不到调节作用比例控制无法消除余差[4]。

(2) 积分调节I

积分常数Ti大小的选择决定了积分作用强弱程度，而积分作用一般会导致系统的稳定性下降。

(3) 微分调节D

当偏差e瞬间波动过快时微分调节器会立即产生响应来抑制偏差的变化使系统更趋于稳定改善了系统的动态性能。

首先在Simulink中搭建模型如下图所示：

图3 Simulink模型图

在上图中PIDController中根据实际更改PID的三个参数，使小车到达稳定状态。在状态空间中根据建立的模型，把实际的系统参数带入A、B、C、D中，从而确定模型的属性。

图4

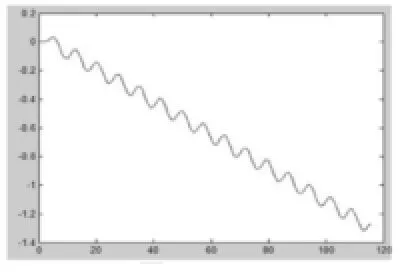
图5

图6

图7

图4 KP=9, Ki=0, KD=0仿真图，控制曲线不收敛，需要增大控制量。

图5 KP=40, Ki=0, KD=0仿真图，闭环控制系统持续振荡。为消除系统的振荡，应增加微分控制参数KD。

图6 KP=40, Ki=20, KD=4仿真图，小车的控制基本稳定，角度基本为0度，但是小车的位置在持续的变化，所以小车有稳态偏差。

图7 KP=40, Ki=20, KD=80仿真图，相比之下小车的位置稳定性大幅度提高，但是如果要达到绝对的稳定，还应通过以下两种方法解决：一，继续调整PID的三个控制参数。二，采用双PID控制。

因此，采用PID控制可以达到工程上的效果，但是需要反复调整三个控制参数才能达到预期效果。从表面上来看带有一定的盲目性，因此本文又尝试结合最优控制的方法。

4、LQR控制算法的设计

LQR控制器的最优反馈增益矩阵为：

K=LQR（A,B,Q,R）

u(k)=-Kx

由原理知，要求出最优控制作用u，除求解代数Riccati方程外，加权矩阵的选择也是至关重要的，下面是几个选择的一般原则：

① 通常选用Q和R为对角线矩阵,当控制输入只有一个时，R为标量数。

② Q的选择不唯一，这表明当得到的控制器相同时，可以有多种Q值的选择，其中总有一个对角线形式的Q。

下面将通过仿真实验求加权阵Q、R与性能指标间的关系：

图8

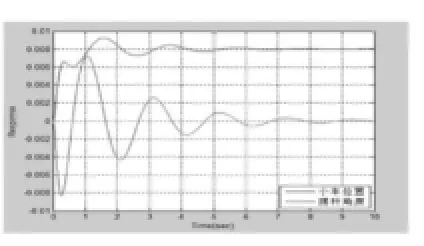
图9

图10

图11

● 在w11=500、w33=500时，K =22.3607 13.5836 -22.3497 2.2314。小车位置和摆杆角度的关系如图8所示。

● 在w11=10000、w33=500时，K =100.0000 23.8060 -13.7383 5.8454。小车的位置和摆杆角度的关系如图9所示。

● 在w11=10000、w33=10000时，K =100.0000 50.1585 -78.6839 19.9598。小车的位置和摆杆的角度如下图10所示。

由图8-10可以看出Q矩阵中的权值对系统的稳定时间、超调量和调整时间有很大的影响。在w11=10000、w33=500时，小车的位置和摆杆的角度有很大的超调量，尤其是摆杆角度超调量更大。这对小车的稳定性是很不利的。所以需调整Q中的权值，来减少超调量和调整时间。

通过大量的实际测试，在w11=10000、w33=10000，系统的调整时间变的最短。同时，系统的超调量和稳定时间也有所减少，是一种比较理想的状况。但是在系统稳定的前期仍然需要调整[7]。

故可得出结论当Q(t)阵中某一元素的权值增大时, 与其相对应的x(t)的动态响应过程好转, ts、td显著下降系统快速性得到一定提高；与此同时，也引进了一些振荡而控制量的幅值会相应增大这表明要求输入能量增大即要提高动态性能必须以比较大的能量消耗为代价。

现保持Q值不变，即w11=10000、w33=10000,改变R。使R=1变为R=3,考擦控制量的变化，对比仿真结果如图11所示，K =44.7214 24.5829 -39.8801 7.0549。

可见当R(t)阵中某一元素的权值增大时控制量幅值相应减小由0.8减少为0.5 ,表明能量消耗随R(t)增大而减小,其对应的动态性能指标有所改善,但并不显著[8]。

通过上面的分析可知，LQR最优控制系统中Q(t)和R(t)的选择是相互制约相互影响的，如果要求控制状态的误差平方积分减少必然会导致增大能量的消耗反之为了节省控制能量就不得不牺牲对控制性能的要求。

5、结论

常规PID控制的效果相比LQR稍差。主要是因为常规PID控制器实质上是一种线性控制器对于像倒立摆这样的非线性绝对不稳定系统控制效果上显得有所不足，但LQR的抗干扰性能及鲁棒性也不是十分的完美，因为LQR是通过对系统进行局部线性化后运用的一种方法[9]。

虽然控制理论在不断的发展新的控制方法不断的出现，但PID控制器因具有结构简单设计原理易于被工程设计人员掌握，鲁棒性强和不需要对象的精确数学模型等优点在工业过程控制中仍然得到了最广泛的应用[10]。然而对于那些复杂如具有延迟非线性和时变的控制系统为了克服传统PID控制的缺点人们把传统PID控制与模糊逻辑神经网络遗传算法等人工智能技术相结合形成智能PID。

[1] 固高科技(深圳)有限公司编著.倒立摆与自动控制原理与实验[M].2005,24-27.

[2] 关天祥,陈玮,罗俊奇.一级倒立摆的建模、仿真与实时控制[J].深圳信息职业技术学院学报,2007,2.

[3] 黄苑红,梁慧冰.从倒立摆装置的控制策略看控制理论的发展和应用.广东工业大学学报，2001,19(3)：49-52.

[4] 李晓燕.平面一级倒立摆系统的智能控制策略研究：[硕士学位论文].山西：太原理工大学，2005.

[5] 宋西蒙.倒立摆系统LQR-模糊控制算法：[硕士学位论文].西安：西安电子科技大学,2006.

[6] 陈华龙,梁慧冰,霍迎辉.四级倒立摆的Lagrange方程建模.广东工业大学学报,2004，21(2)：59-63.

[7] 朱江宾,易建强.二级倒立摆的摆起控制.系统仿真学报.2003,15(7)：1043-1045.

[8] 张铮等编著.MATLAB在控制系统中的应用.北京：电子工业出版社,2007,5.

[9] 朱文凯，袁桂娥，朱学峰.倒立摆的PID与LQR控制算法的对比研究.广东自动化与信息工程，2006，(2)：1-3.

[10] 吴文进,葛锁良.基于LQR最优调节器的二级倒立摆控制系统.安庆师范学院学报（自然科学版）,2007,13(2)：32-34.

Design of Single Inverted pendulum based on PID and LQR

Cheng Minghe, Chen Cang

（Changan University, Shaanxi Xi'an 710064）

In this thesis single inverted pendulum model was built. And on this basis, through MATLAB simulation tools, inverted pendulum PID and LQR control algorithm was carried on the design and simulation. In general, the LQR control algorithm is superior to the control performance of PID control algorithm.

Single inverted pendulum; PID; LQR

U462.1

A

1671-7988 (2017)05-01-04

程明贺，（1993-）男，硕士研究生，就读于长安大学。研究方向：数字图像处理。