全球大于或等于8.5级特大巨震的周期性分析

徐清华，杨林根

（1.淮北市人民防空和防震办公室，安徽 淮北 235000；2.巢湖市地震办，安徽 巢湖 238000）

0 前言

某一时间序列的历史数据，包括基本模式和随机起伏，预测就是力图将基本模式从随机性变化中分解出来，用基本模式来推测未来[1]。方差分析叠加周期外推法作为统计预报实践中的一类时序周期外推法，在气象、水文、农业、地质等各方面已得到大量的应用，但在地震预测预报方面的应用尚不多见。

方差分析叠加周期外推法是一种统计分析方法。它可以分析与地震活动有关因子的变化是否异常，也可以用它摸索地震本身的活动规律进行外推预报。不过，这两者都必须依附在这些因子变化的过程中确实存在有周期性变化的客观事实上。

地震是一种自然现象，一般是不可能有严格的周期，因此，本文所讨论的的周期都是指具有某种概率的周期性。当然，如果有一些因子能够呈现周期，只是在某一时段受到其他因子的影响，其运行规律受到破坏，那么我们可以应用这种方法找出这一异常的起点，进行试验和探索。

1 方差分析叠加周期外推法简介

1.1 基本原理

方差分析叠加周期外推法就是把某一要素序列按不同的间隔进行分组，并分别计算出不同组别下的组间方差与组内方差的比值F，通过F大小的比较，选取出最大的F进行某信度下的周期是否显著的检验，通过检验的可以确定在该信度下可能存在相应的周期，然后从原序列中剔除该周期的影响，在残差序列中再找下一个周期，依次类推，直至残差序列稳定（即F检验不显著）为止，最后再将找出的几个相应的周期特征值分别相加，通过时间外延来预报某些要素的未来变化。具体方法流程见图1。

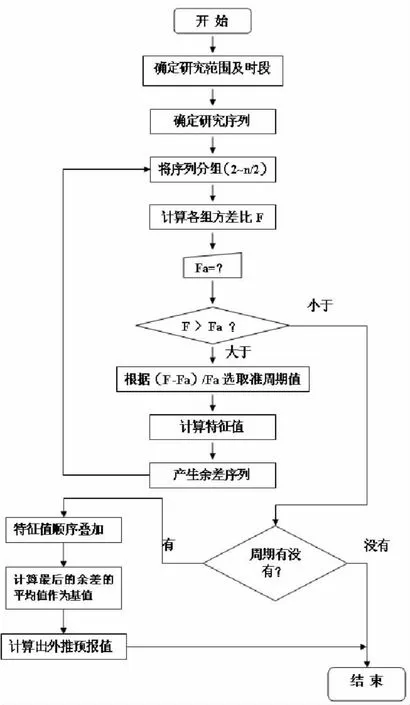
图1 方差分析叠加周期外推法的具体步骤Fig.1 Concrete steps of variance analysis superimposed by periodic extrapolation

1.2 计算方法

1.2.1 组间离差平方和与组内离差平方和的计算

把n年观测数据X1，X2，……Xn排列成表1的形式，其中：j表示组别，j=1，2,……b；i为每组的项数，其中，T为总数；Tj为每组的合计数；为每组的组平均值。

表1 试验周期分组表Table 1 Grouped table of periodic test

组间离差平方和与组内离差平方和的计算公式为：组间离差平方和组内离差平方和表示各组平均值对总平均值的离差平方和，在前面再乘以a，这是因为考虑到每组内又有a项的关系，它表达了组与组之间数据的差异情况。组内离差平方和是指同组之内各个数据Xij对组内平均值的离差平方和，即它代表了每组内部数据的差异情况，由于共有b组，还要把各组的相加，所以

1.2.2 方差比F的确定与F检验

由于做周期分析时，事先并不知道周期数目，因些需要从可能存在的周期中反复排列各种数值根据方差比：

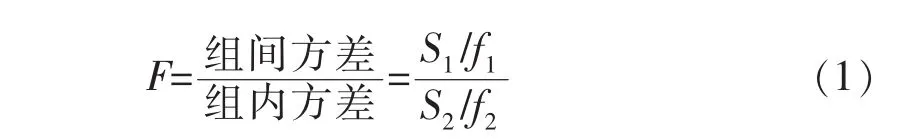
式（1）中，S1，S2分别为组间离差平方和与组内离差平方和；f1、f2分别为组间离差平方和与组内离差平方和的自由度。f1=b-1，f2＝n-b。

方差比F在一定的条件下可以证明是一个随机变量，而且是服从F分布的。F分布可以计算，也可用F分布表查询，因此可以用F检查的方法来检验该组周期特征是否具有显著性。具体计算步骤见图1

2 实例分析

2.1 资料与资料时段的选定

（1）公元1900年后的地震事件参数主要是由地震台网测定的，其参数相对完整和准确，1900年之前的地震事件，通常是历史记载的地震信息资料确定的，由于历史资料的局限性，故地震事件的缺失（不完整性）和地震参数的误差都很大[2]，所以地震目录从1900年开始。但又考虑到1897、1898、1899连续三年都有MS≥8.5级特大巨震记录，这三年的资料不仅具有统计意义，而且也有一定的可信度，因此统计时段选定从1897年开始。

（2）2011年之前的地震统计使用宋治平等编著的 《全球地震目录》[3]，2011年后资料来源于“地震科学数据共享网” 的中国地震台网（CSN）地震目录。具体编目见表2。

2.2 地震震级的选定与资料的处理方法

刘瑞丰、陈运泰等将中国地震台网与美国地震台网测定震级进行对比后，认为：由于使用的震级计算公式与仪器记录分向的不同，我国测定的MS值总体上要比NEIC测定的值平均偏高0.2级。如果以NEIC测定的震级为基准，对于3.5～4.5级的地震，IGCEA测定的震级比NEIC测定的震级偏高0.3级；对于5.0～6.5级的地震，IGCEA偏高0.2级；对于7.0级以上的地震，IGCEA偏高小于0.1级[4]。由些可见，震级越小，差别越大；震级越大，差别越小。

另外，由于MS面波震级存在大震震级饱和现象，当MS超过8.6级后，测定的MS值却很难再增上去。而NEIC震级仍按地震破裂大小计算震级。同一地震，MS震级却低于NEIC震级。为了保证统计样本的准确性，提高统计资料的可信度，本文选择MS≥8.5级作为起始震级。

具体方法：文中不考虑震级大小在时间上的关系，仅将该年是否发生 “MS≥8.5级特大巨震作为研究对象”。将发生过MS≥8.5级特大巨震的年份记作 “1”，没有发生过MS≥8.5级特大巨震的年份记作 “0”，一年中如果发生多次MS≥8.5级特大巨震只记一次。这样就产生了以 “0”和 “1”以时间为序的 “脉冲序列”，时间单位为年。具体记录见表3。

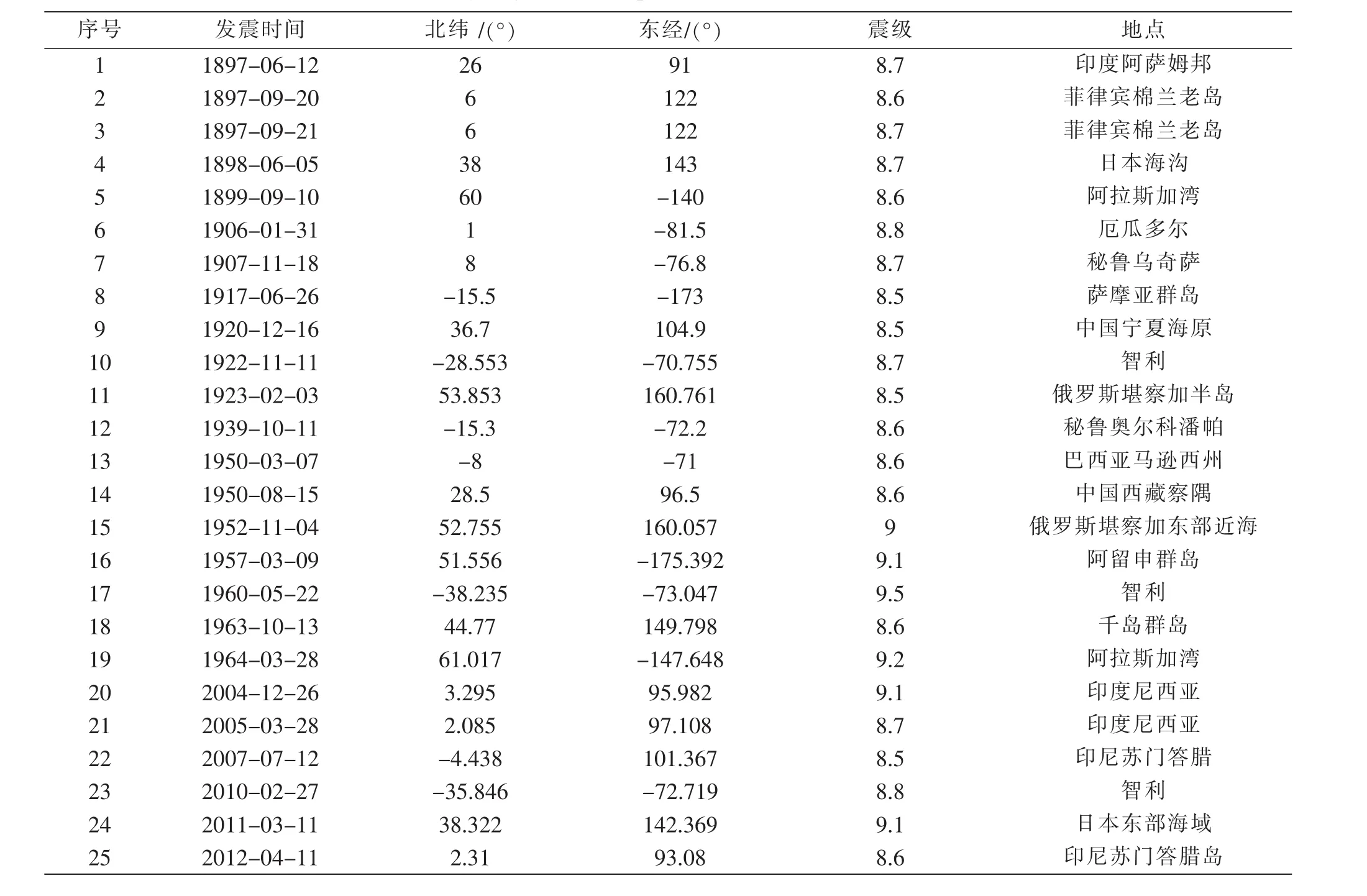
表2 1897—2015年全球大于等于8.5级以上地震目录Table 2 Catalog of global earthquakes with MS≥8.5 from 1897 to 2015

表3 1897—2015年全球是否发生大于等于8.5级以上地震统计表Table 3 Statistics of whether global earthquakes with MS≥ 8.5 occurred from 1897 to 2015

2.3 统计过程

采用方差分析周期外推法，按2至59年分别为1组逐一排列，分别求出其F值，并找出能通过α=0.10 F分布表检验的组数为选出周期，再将找出的周期特征值从原序列中相应扣除，得到新序列再进行下一轮周期的筛选。

2.4 分析结果与结论

经过方差分析周期外推法分析计算获取按组数为41、5、53、29、33、23、21、4组计算统计的结果于表4。

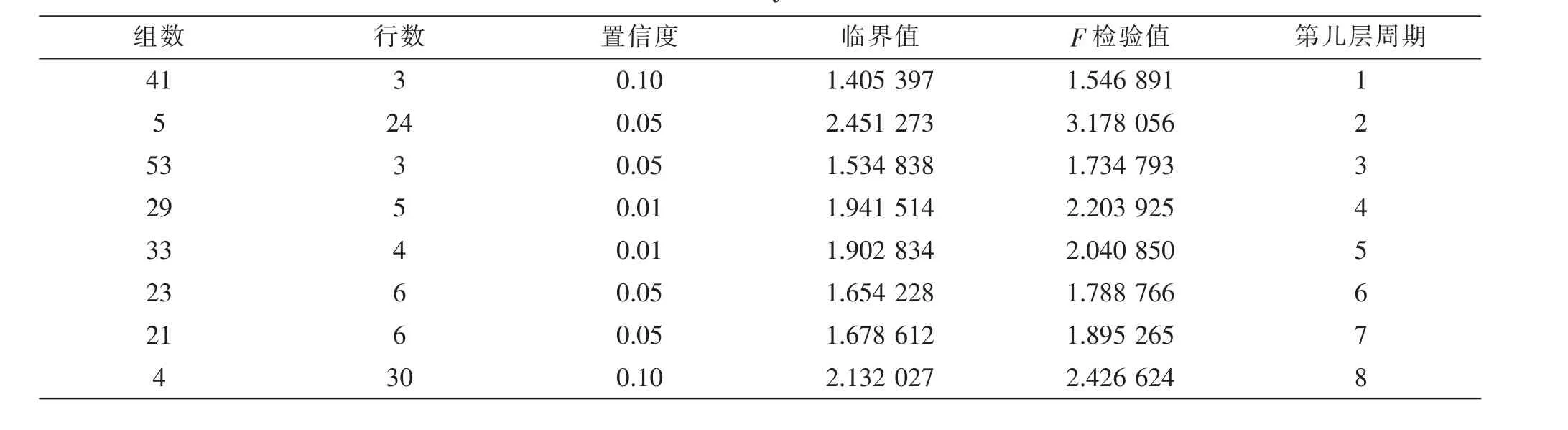
表4 通过α=0.10 F分布表检验的记录表Table 4 Record form tested by α=0.10 F distribution table

表4中的 “组数”即为发生大于等于8.5级地震的准周期（年）， “行数”是相应准周期（年）下的周期数。

8个准周期的特征值分别是：

（1） 准 周 期 41 年 为 ： 0.33、0.67、0.33、0.00、 0.00、 0.00、 0.00、 0.00、 0.00、0.33、0.33、0.00、 0.33、 0.00、 0.33、 0.00、 0.00、 0.00、 0.00、0.33、 0.33、 0.00、 0.33、 0.33、 0.00、 1.00、 1.00、0.00、 0.33、 0.00、 0.00、 0.33、 0.33、0.33、0.00、0.00、 0.00、 0.00、 0.00、 0.00、 0.00。

（2） 准周期 5年为： 0.25、 0.00、 0.03、 0.11、0.03。

（3） 准 周 期 53 年 为 ： 0.84、 0.61、 0.83、0.47、 0.64、 0.39、 0.50、 0.83、 0.58、 0.86、 0.84、0.39、 0.27、 0.46、 0.32、 0.33、 0.33、 0.38、 0.46、0.15、 0.50、 0.33、 0.21、 0.79、 0.49、 0.33、 0.50、0.38、 0.29、 0.32、 0.00、 0.17、 0.21、0.29、0.49、0.33、 0.50、 0.38、 0.29、 0.32、 0.33、 0.17、 0.54、0.13、 0.49、 0.33、 0.50、 0.38、 0.29、 0.32、 0.17、0.17、 0.21。

（4） 准 周 期 29 年 为 ： 0.20、0.35、0.32、0.06、 0.00、 0.20、 0.16、 0.12、 0.14、 0.37、 0.29、0.20、 0.15、 0.25、 0.13、 0.05、 0.25、 0.25、 0.09、0.16、 0.35、 0.09、 0.18、 0.48、 0.26、 0.10、 0.30、0.41、 0.19。

（5） 准 周 期 33年 为 ： 0.28、 0.21、 0.25、0.22、 0.31、 0.16、 0.23、 0.00、 0.08、 0.23、 0.20、0.31、 0.17、 0.23、 0.27、 0.36、 0.22、 0.09、 0.21、0.20、 0.45、 0.31、 0.19、 0.12、 0.17、 0.27、 0.09、0.22、 0.09、 0.15、 0.30、 0.09、 0.30。

（6） 准 周 期 23 年 为 ： 0.08、0.10、 0.16、0.11、 0.02、 0.06、 0.15、 0.05、 0.04、 0.11、 0.08、0.08、 0.03、0.00、 0.06、0.01、 0.02、 0.20、 0.10、0.16、 0.13、 0.18、 0.12。

（7） 准 周 期 21 年 为 ： 0.10、 0.05、 0.05、0.00、 0.01、 0.05、 0.03、 0.04、 0.12、 0.17、 0.11、0.00、 0.00、 0.07、 0.02、 0.09、 0.13、 0.07、 0.08、0.06、 0.11。

（8）准周期 4年为：0.00、0.01、0.02、0.05将相应的准周期特征值叠加值与原始数据得拟合数据曲线见图2。

3 分析

（1）经过严格的理论计算，且通过α=0.10 F检验，获取了8个准周期值，8个准周期值分别为41、 5、 53、 29、 33、 23、 21、 4 年， 其中 4、 5 这两个准周期值是地震活跃期间的特征值，在地震活跃期中有一定的预测意义。

（2）该方法从2013年底试用2次，分别预测下一年没有大于等于8.5级地震的发生，均已成功。

（3）将相应的准周期特征值叠加值与原始数据得拟合方法，预测2016年发生特大巨震的概率几乎为0，即发生MS≥8.5级特大巨震的可能性不大。

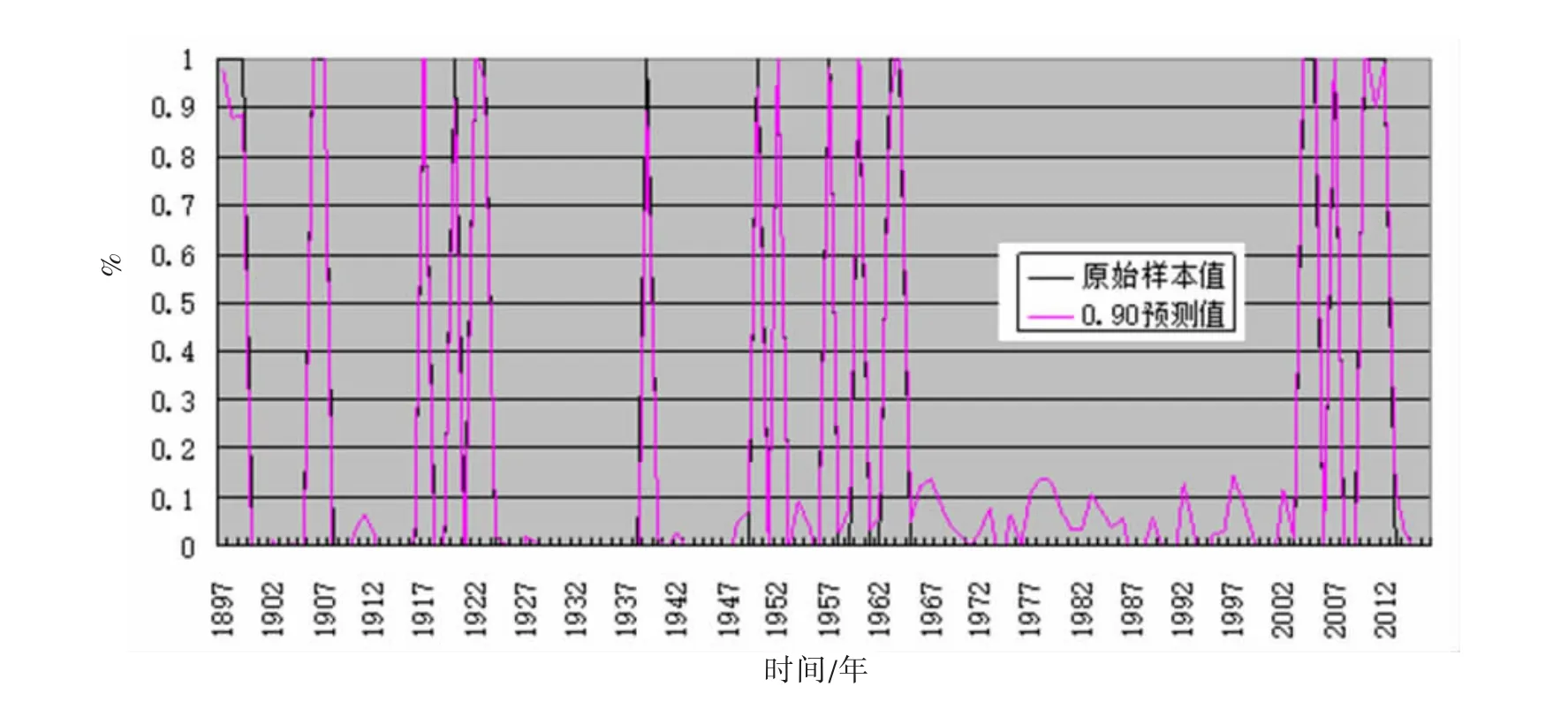
图2 全球大于等于8.5级以上地震方差分析周期外推拟合曲线图Fig.2 Fitting curve of global earthquakes with MS≥8.5 through variance analysis superimposed by periodic extrapolation

（4）将相应的准周期特征值叠加值与原始数据得拟合方法，预测下一次发生大于等于8.5级地震可能在2029年前后。

4 结语

（1）方差分析叠加周期外推法是数理统计上常用的方法，用于地震预测预报只是一种尝试。它可以用来研究地震震中在空间上的迁移特性，也可分析在时间序列、震级强度变化上是否具有周期性。

（2）由于历史地震目录来源不同，定级标准不同，准确性也有所不同。本文采用特大巨震作为研究对象，但仅考虑将某年有没有发生过MS≥8.5级特大巨震作样本，并采用了α=0.10 F分布表检验，也就是说置信度达90%，但仍然肯定还有因资料准确性而带来的问题。例如如果采用美国国家地理信息中心关于特大巨震的目录[5]，仅至2005年和我们现用的目录就有三个地震记录的误差。美国国家地理信息中心的目录少记录了1917年6月26日萨摩亚群岛8.5级、1939年10月11日秘鲁奥尔科潘帕8.6级地震，多记录了和1965年2月4日阿留申群岛8.7级地震，显然对本文的统计结果影响不大，但在置信度上和准周期的个数上还是有点误差，因此，统计分析的结果只能作为参考。

（3） 预测值与实测显然存在一定的误差，但方法的意义在于应用统计理论上有了一个时间预测，这对缩小了监视时间段，对确定重点监视时段，从某种意义上有着其一定的积极意义。另外通过分析出的准周期值，这为研究地震机理，探索导致特大巨震发生的外部环境和演变规律提供研究方向上的参考。

参考文献：

[1]邢兰辉，吕惠萍，张锦辉.周期叠加方差分析法预报河川径流量[J].水文，2007，27（4）：41-44.

[2]宋治平.全球及各地震区带强震活动周期特征 [J].地球物理学报，2013，56（6）：1 868-1 876.

[3]宋治平，张国民，刘杰，等.全球地震目录[M].北京：地震出版社，2011.

[4]刘瑞丰，陈运泰，Peter，等.中国地震台网与美国地震台网测定震级的对比 （Ⅱ）--面波震级[J].地震学报，2006，28(1)：1-7.

[5]胡辉，韩延本.全球巨震的天文背景[J].天文研究与技术,2006，3（1）：77-83.