地震作用下高层隔震结构高宽比限值计算

刘彦辉，林港源，杨鹏程，金建敏

（广州大学 减震控制与结构安全国家重点实验室培育基地，广州 510405）

随着经济水平的进步与隔震技术的发展，隔震技术在高层结构中得到使用。高层隔震结构某个方向高宽比较大时，由于地震作用在该向产生的倾覆力矩较大，因而在地震发生时，隔震层将承受很大的弯矩，这时有的隔震支座可能受拉进入屈服破坏（隔震支座普遍存在竖向抗拉能力差的弱点），而有的支座承受过大的压力，这都会使得结构存在整体倾覆的危险。因此限制结构的高宽比是解决高层隔震结构倾覆破坏问题的一种有效方法。李宏男[1]分析了场地条件、隔震层刚度和结构类型等因素对高宽比限值的影响，吴香香[2]在此基础上分析了竖向地震对隔震结构高宽比限值的影响，祁皑[3-5]对隔震结构的高宽比限制进行了系统性的研究，在橡胶隔震支座不产生拉应力，压应力不超过30 MPa的条件下，采用三质点等效模型推导出多振型高宽比限值计算公式。王栋[6]对不同高宽比的基础隔震高层结构进行振动台试验。

本文以上基础上，将高层隔震结构体系模型进行简化，根据 《建筑抗震设计规范》（GB50011-2010）规定，橡胶隔震支座拉应力不超过1 MPa，压应力不超过30 MPa，以结构不出现倾覆破坏为前提条件，推导了高层隔震结构高宽比限值计算公式，并得出高层隔震结构在不同设防烈度、不同场地类别、不同地震分组下的高宽比限值，分析了高宽比限值与隔震结构周期的关系。

1 高层隔震结构高宽比限值公式推导

1.1 基本假定

参照文献[3]、[4]、[7]， 本文研究对象为采用叠层橡胶隔震支座的高层隔震结构，做出以下假定：①隔震支座拉应力不超过1 MPa，压应力不超过30 MPa；②隔震支座对称布置；③隔振支座的水平刚度和竖向刚度与隔震支座面积成正比；④隔振层顶部梁板结构为刚性层；⑤隔震结构位移反应以第一振型为主，第一振型近似乎平动竖直直线。

1.2 边缘隔震支座受力分析

边缘隔震支座所受轴力是由水平地震作用、重力荷载表表值、竖向地震作用产生的倾覆力矩引起的和重力荷载表表值、竖向地震作用产生的竖向力引起的。

1.2.1 边缘隔震支座受倾覆力矩产生的轴力

（1）水平地震作用引起的轴力。根据隔震结构基本振型的特点（如图1左图细线所示），可以近似假定各质点的相对水平位移Xi均相等（如图1左图粗线）即Xi=η′H0。近似后由左图简化为右图所示振型特点。其中η＇为比例常数；H0为隔震层质点计算高度[8]。

图1 隔震结构基本振型Fig.1 Vibration mode of isolation structure

为了方便计算，做以下定义：

隔震层以及上部结构各层的质量相近，都为m，即m0=m1=m2=…=mn=m。

上部结构每一层层高相同，隔震层层高为上部结构各楼层层高的一半高度，即2h0=h1=h2=…=hn=h。

水平地震作用在结构底部的总弯矩

将式（1）代入（2）中得

式（3）中，α′为隔震结构基本周期的水平地震影响系数，HS为上部结构的总高度HS=nh，GS为上部结构重力荷载代表值GS=nm，n为建筑的层数。

根据 《高层建筑混凝土结构技术规范》，建筑高度高于24 m时为高层建筑[10]。令：

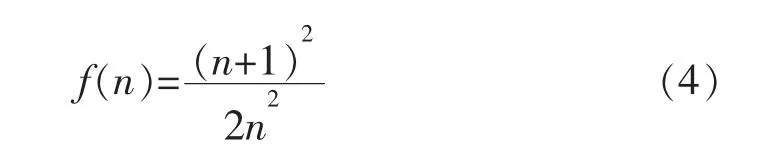
对上式求导可知当n≥0时 f′（n）≤0，为单调递减函数。在保证结构安全的前提下，n=8时。 f（n）取到最大值， f（8）=0.633。 由此得：

MEh=0.633α′GSHS（5）

根据基本假定（2），由于支座的布置是对称的，所以隔震层的转动刚度：

式（6）中 ：Kvi为支座的竖向刚度；B为隔震层的宽度；n1橡胶支座的个数；ηi=2xi/B，xi表示支座i到隔震层中心的距离。

水平地震作用在边缘隔震支座上的轴力：

（2）重力荷载表表值、竖向地震作用引起的轴力。

将隔震前后的频率比取R=T11/Tυ1=2，则有[4]：

竖向地震作用在边缘隔震支座上引起的轴力：

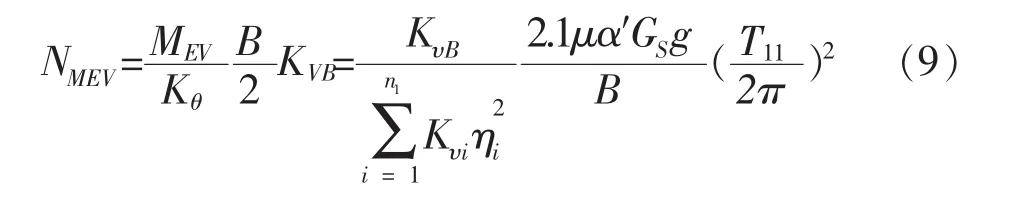
重力荷载代表值在边缘隔震支座上引起的轴力：

式中，T11为隔震后结构的周期，Tυ1为非隔震结构的周期，ω11为隔震结构的基本频率。1.2.2边缘隔震支座受竖向力产生的轴力

（1）重力荷载代表值产生的竖向力引起的轴力NFEV

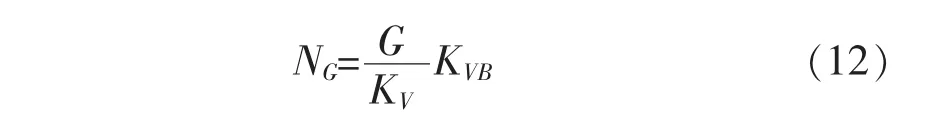
式中：G为结构总重力荷载代表值，KVB为边缘支座的竖向刚度，KV为隔震层总竖向刚度。

（2）竖向地震作用产生的竖向力引起的轴力NFEV。

《建筑抗震设计规范》规定，建筑隔震结构竖向地震作用为:

隔震支座所受轴力：

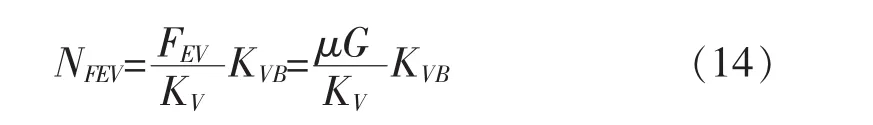
式中，μ为竖向地震影响系数，其取值为别为0 （7 度）、 0.2 （8 度）、 0.4 （9 度）。

1.3 高宽比限值公式

1.3.1 边缘隔震支座上拉应力不超过容许值时的轴力最不利组合

当竖向地震作用方向向上，边缘隔震支座很可能会产生拉应力并超出容许应力值，为了保证支座的拉应力在容许应力值之内，应满足以下条件：

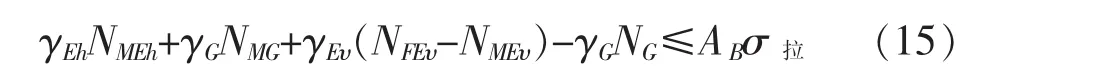
式中， 系数 γEh取 1.3； γEυ取 1.0； γG对结构有利时取1.0，对结构不利时取1.2；AB为结构一侧边缘支座的面积；σ拉为支座的拉应力容许值。

由基本假定（3）可以得到：

令A=kb/βb，kb为结构隔震层的水平刚度。

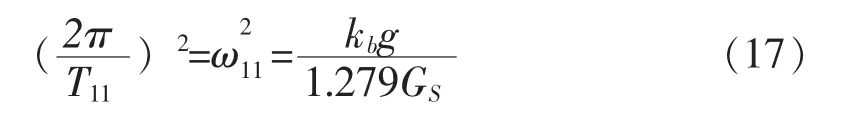
将式（7）、（9）、（12）、（14）、（16）、（17）代入（15）得到：

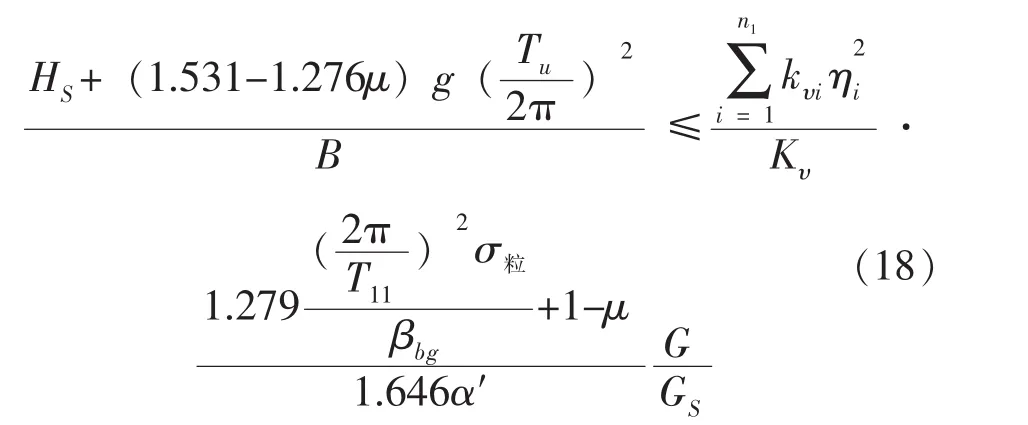
1.3.2 边缘隔震支座上压应力不超过容许值时的轴力最不利组合

当竖向地震作用方向向下时，边缘隔震支座上的压应力可能会超过压应力容许值，为了保证支座的压应力在容许值范围之内，应满足一下条件：

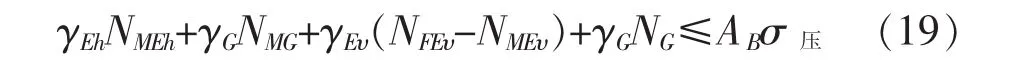
式中， 系数 γEh取 1.3； γEυ取 1.0； γG对结构有利时取1.0，对结构不利时取1.2。

将式 （7）、（9）、（12）、（14）、（16）、（17） 代入式（19）得：

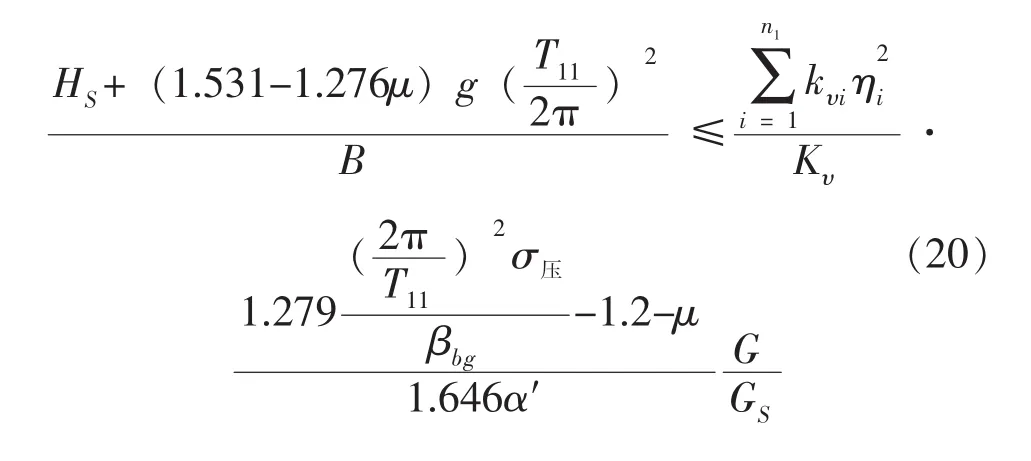
2 高层隔震结构高宽比限值与结构基本周期的关系

由式（18）、（20）得到： 高宽比限值在边缘隔震支座上拉应力不超过容许应力值时

上式可化为：

因此，可以得知当高宽比限值由隔震支座边缘支座拉、压应力不超过容许值时，可以将临界周期定义为：

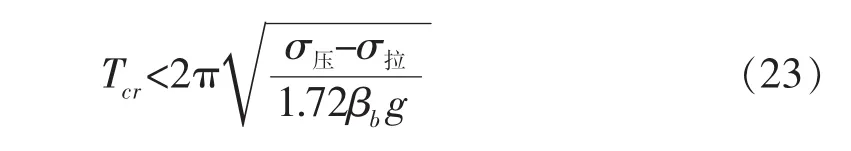
式中：βb=kb/A。

βb的取值与隔震支座的选取有关，考虑到高层隔震结构较多使用的隔震支座的直径600 mm、1 200 mm，根据文献 [4]，取βb的平均值：3.78×106，根据假定（1），隔震支座的压应力容许值为30 MPa，拉应力容许值为1 MPa，由此可得临界周期：Tcr=4.239 s。

将式 （21）左边式子第二项进行转化得：

式中ηh0为结构在第一振型下的水平位移，与结构宽度B的比值很小，可以忽略不计。

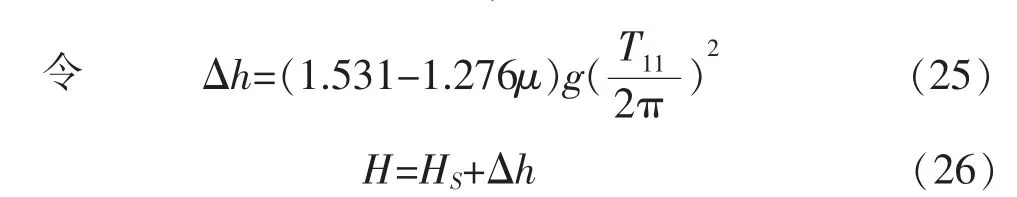
对式（21）、（29）分析高宽比与隔震结构周期的关系：

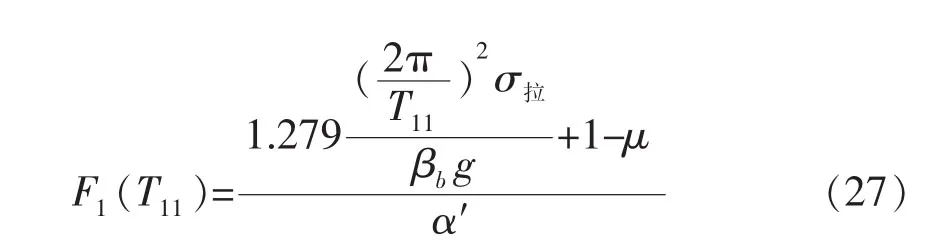
通过F1（T11）的导数，可以知道隔震结构高宽比与结构周期的单调关系。

（1） 当 Tg＜T11＜5Tg时，

式中：Tg为场地特征周期。

对 F1（T11）求导可以得到

本文所研究的为高层隔震结构，2s≤T≤5s，当阻尼比0.05≤ζ≤5时，设防烈度7度~9度，当时 Tg＜T11＜5Tg时， F1′（T11）＞0， 高宽比随着结构周期的增大而增大。

在场地特振周期Tg为0.25 s，0.30 s，0.35 s，0.40 s时T11＜5Tg≤2s，在图2至图4中可以省略。当 Tg取值为 0.45 s， 0.55 s， 0.65 s 时， 2 s＜T11＜5Tg时， F1′（T11）＞0， 高宽比在 2 s＜T11＜5Tg时随着结构周期的增大而增大。

（2） 当 T11＞5Tg时，

式中，η1为直线下降段的下降倾斜调整系数。

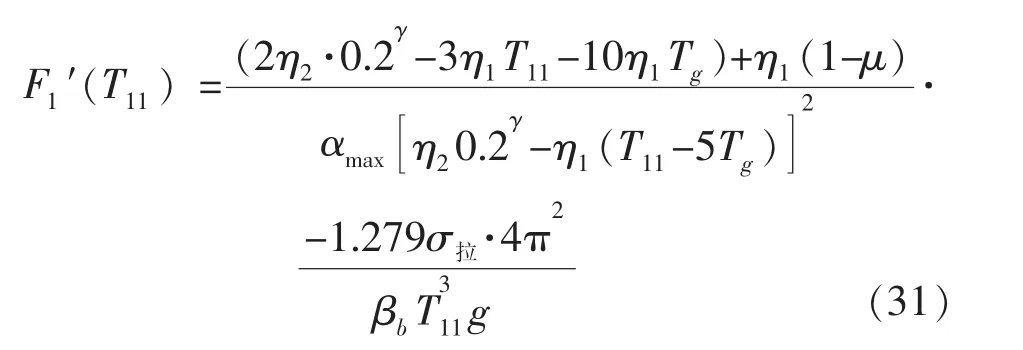
当 ξ取值0.05~0.2间时，Tg取值0.25~0.65间，同上推导可得：F1′（T11）在 取值前半段为负后半段为正，在不同场地周期下分界线不同，高宽比总体趋势是先下降后上升。高宽比在Tg＞5Tg时随着结构周期的变化参考图2至图4。

高宽比限值在边缘隔震支座上拉应力不超过容许应力值时，同上化简可以得到：

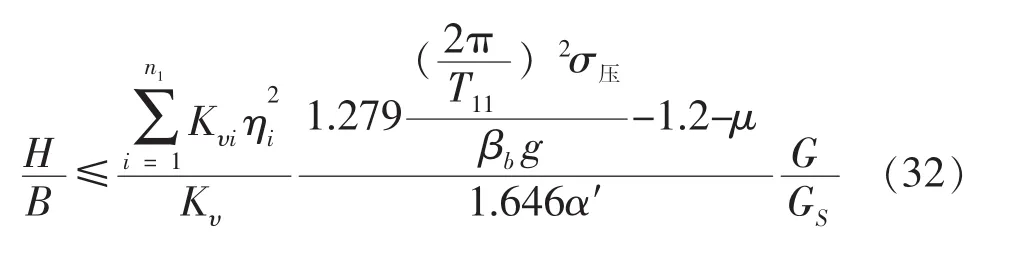
对F2（T11）求导，可以确定高宽比与结构周期的单调关系。

同上推导分析可得， 当 Tg＜T11＜5Tg时：

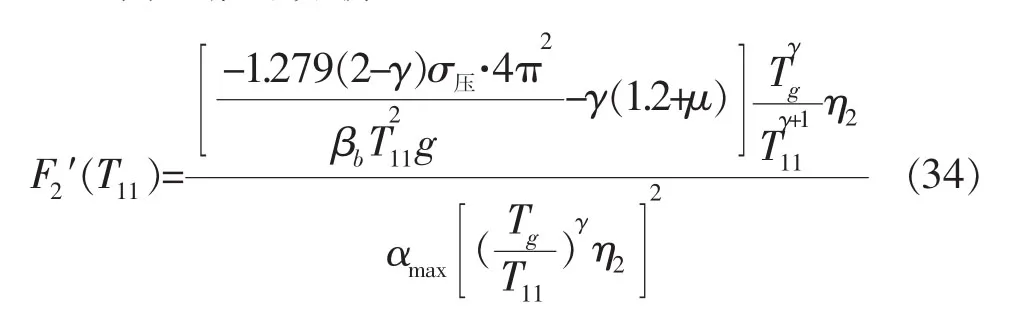
由上式可知： F2′（T11）＜0， 高宽比在 Tg＜T11＜5Tg时随着结构周期的增大而减小。

（3） 当 Tg＞5Tg时 ：

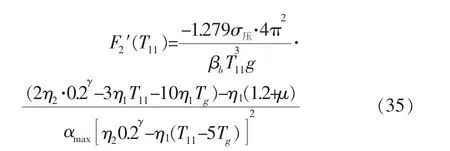
由上式可知： F2′（T11）＜0， 高宽比在 Tg＞5Tg时随着结构周期的增大而减小。

由此可知当边缘隔震支座压应力不超过容许压应力时，高层隔震结构的高宽比随结构周期的增加而降低。

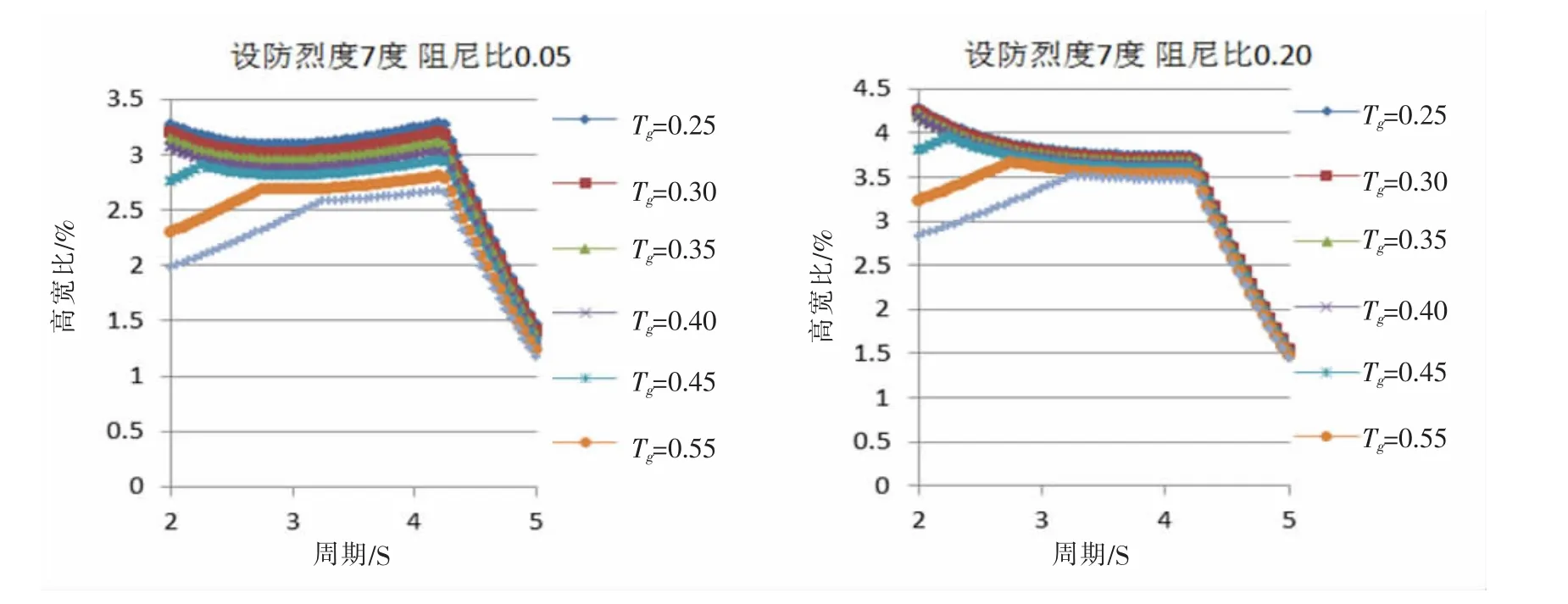
图2 7度地区高层隔震结构高宽比限值与结构周期的关系Fig.2 The relationship between the height-width ratio of the high-rise seismic structure of the 7 degree area and the structural period

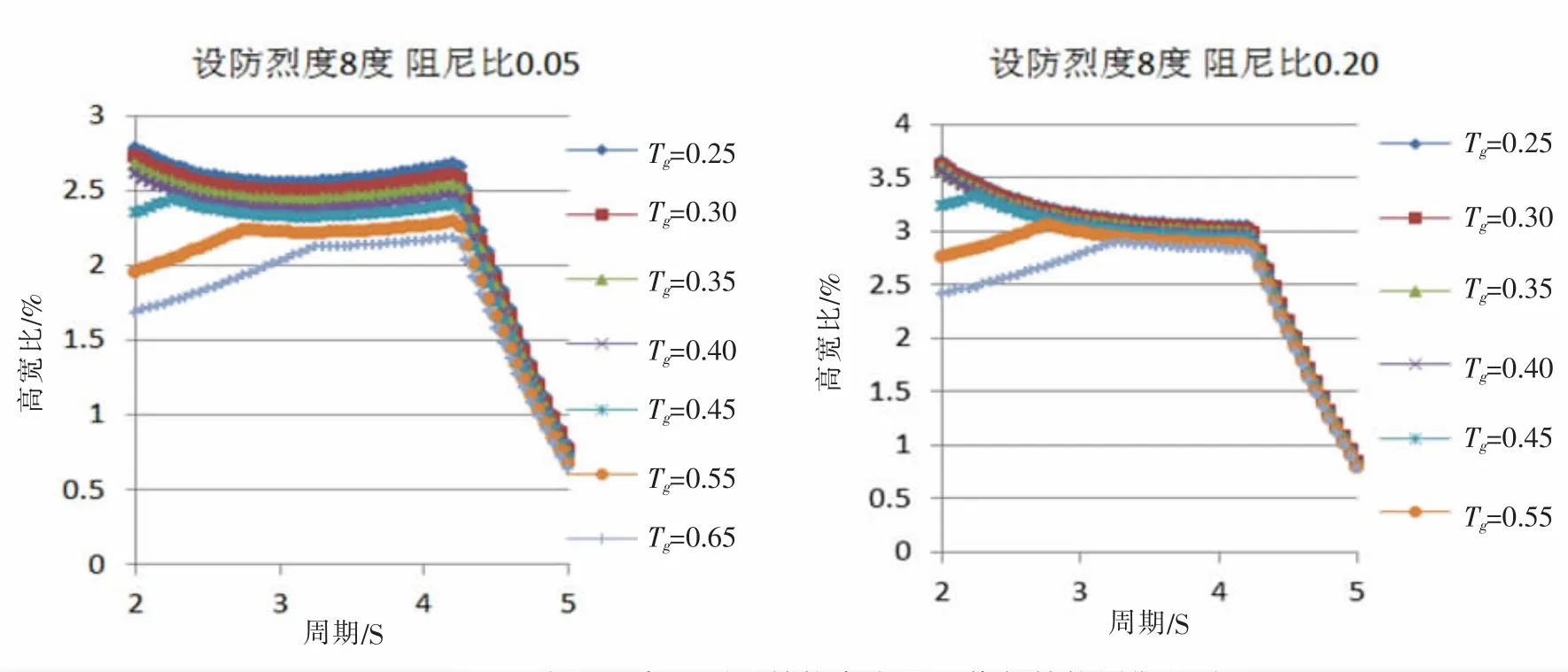
图3 8度地区高层隔震结构高宽比限值与结构周期的关系Fig.3 The relationship between the height-width ratio of the high-rise seismic structure of the 8 degree area and the structural period

3 高层隔震结构的最大基本周期Tmax

3.1 边缘隔震支座压应力不超过压应力容许值的最大基本周期

由式（20）可以得到

整理后可以得到压应力不超过容许值时的最大基本周期（表1）：

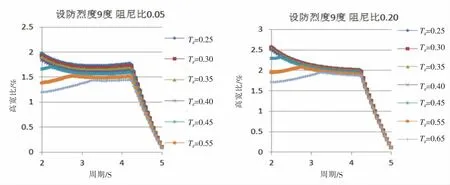
图4 9度地区高层隔震结构高宽比限值与结构周期的关系Fig.4 The relationship between the height-width ratio of the high-rise seismic structure of the 9 degree area and the structural period

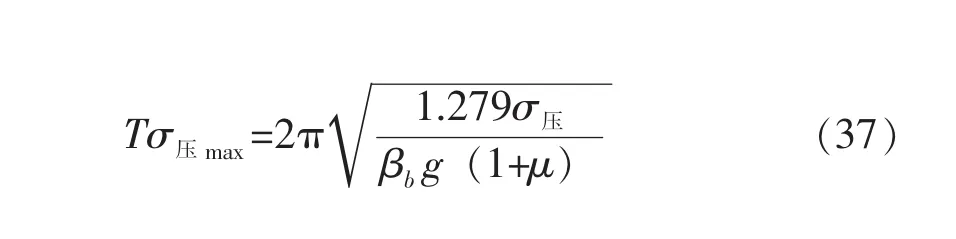
表1 隔震支座压应力控制下的Tσ压maxTable 1 Tσ压maxconfined by the Compressive stress of isolation bearing

3.2 结构受边缘隔震支座最大容许位移 不超过限值的最大隔震基本周期

高层隔震结构隔震层的最大水平位移应满足：

当 Tg＜T＜5Tg时

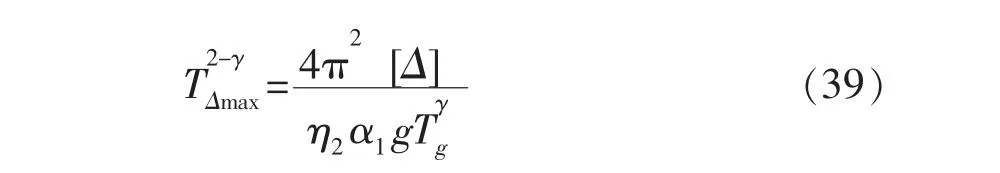
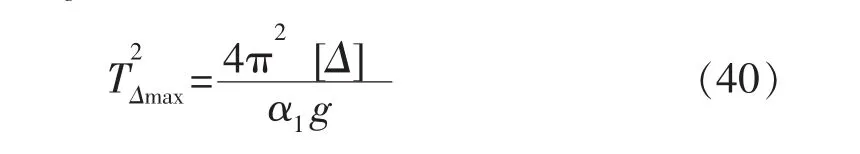
由上式可以知道，TΔmax与隔震支座最大容许位移、阻尼比，结构的抗震设防烈度、场地类别，表2和3给出了隔震支座最大容许位移为300 mm与400 mm时不同场地类别、设计分组、设防烈度及阻尼比所对应的TΔmax。

当 T＞5Tg时

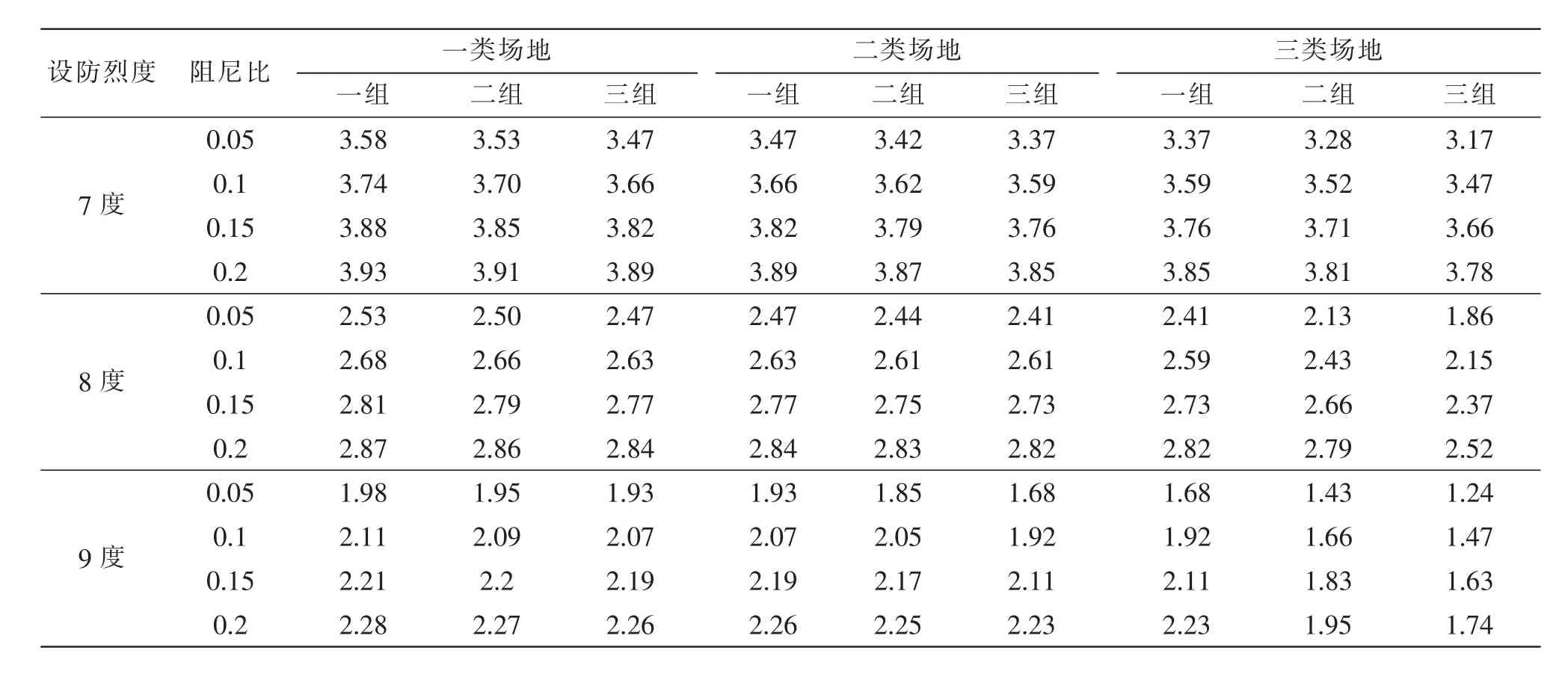
表2 最大容许位移 [Δ]=300 mm控制的TΔmaxTable 2 TΔmaxconfined by the allowed displacement of rubber bearings[Δ]=300 mm

表3 最大容许位移 [Δ]=400 mm控制的TΔmaxTable 3 TΔmax confined by the allowed displacement of rubber bearings[Δ]=400 mm

3.3 高层隔震结构最大基本周期的确定

通过上文分析可得：高层隔震结构的最大基本周期应为：

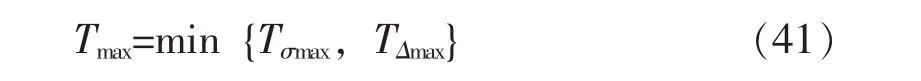
通过对比表4和表5分析得到最大的基本周期应为。

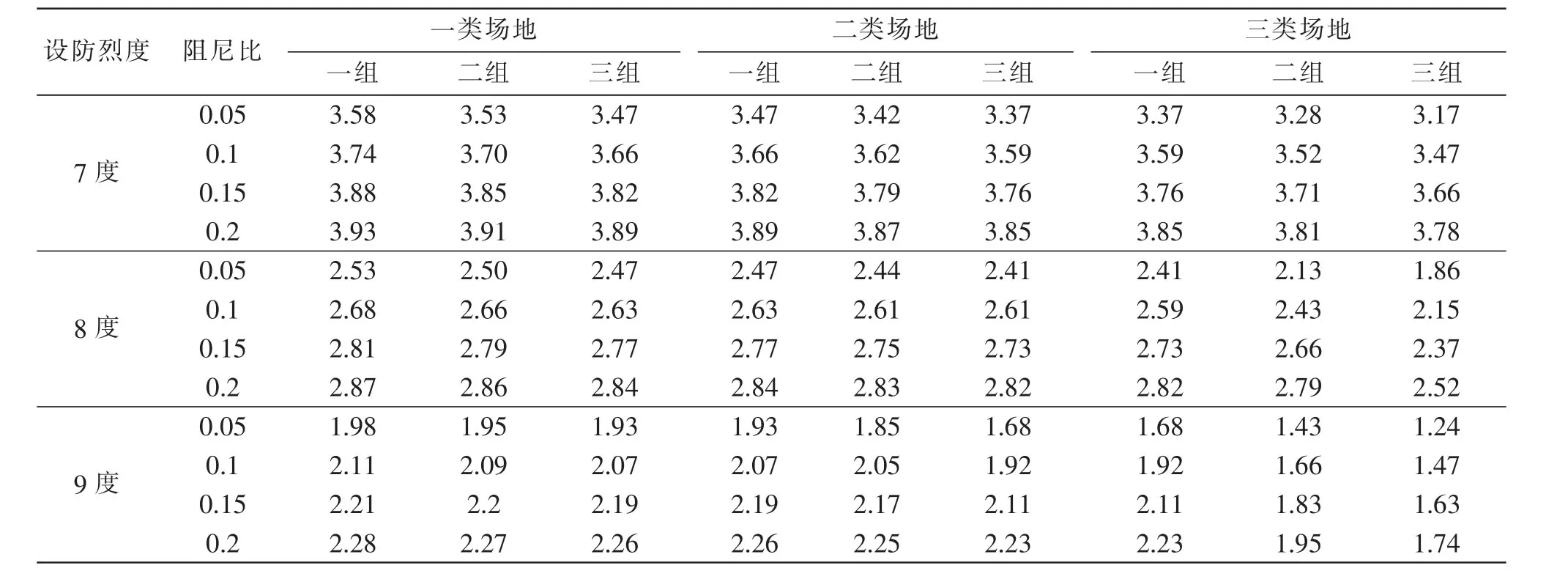
表4 [Δ]=300 mm时高层隔震结构最大基本周期TmaxTable 4 The maximum periods of high-rise base-isolated structure

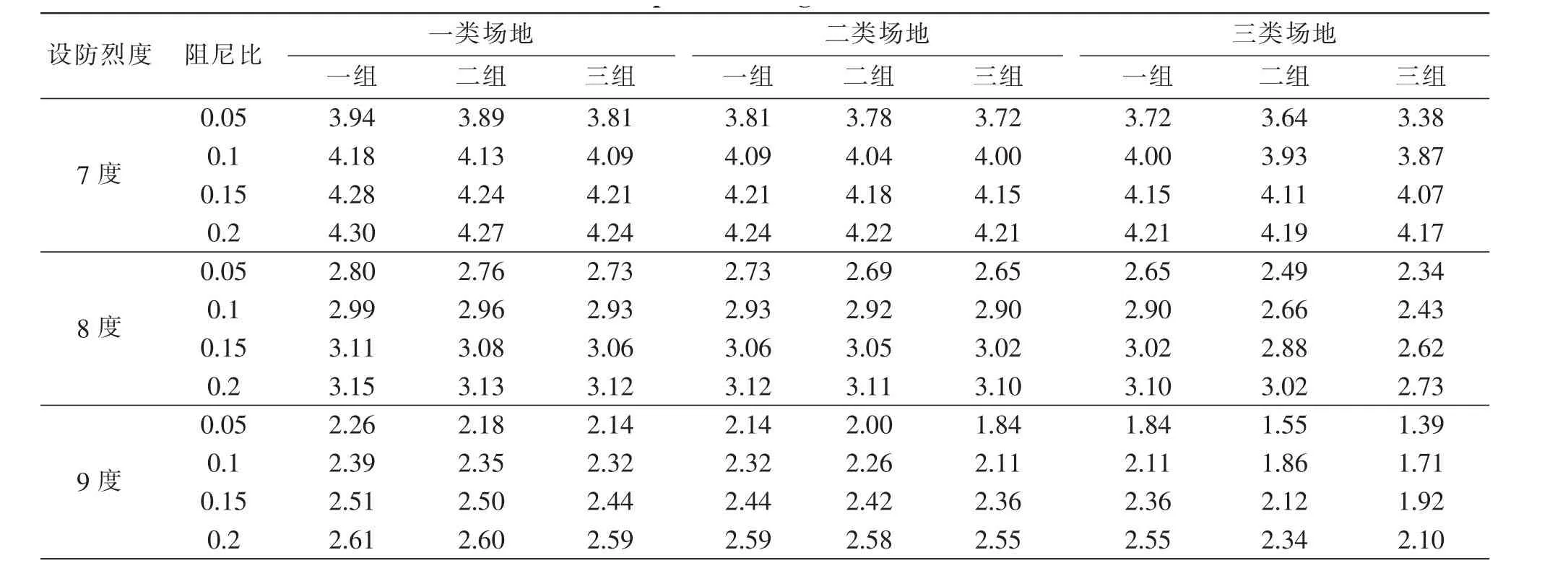
表5 [Δ]=400mm时高层隔震结构最大基本周期TmaxTable 5 The maximum periods of high-rise base-isolated structure

4 高层隔震结构高宽比限值的确定

根据本章的推导可知，高层隔震结构的高宽比限值与结构的基本周期、隔震支座的布置、隔震层的阻尼比、设防烈度、场地类别参数有关。以三跨隔震结构为例 （图5），建筑类别为丙类，基本风压为0.40 kN/m2，地面粗糙度为B类，风荷载体型系数为1.3，抗震设防烈度为8度，基本地震加速度为0.2 g，设计地震分组为第二组，场地类别为II类，场地特征周期为0.40 s，隔震支座的布置如表6、7。

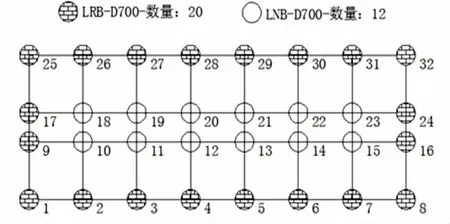
图5 三跨隔震结构支座布置Fig.5 The arrangement of isolation bearing of three-span baseisolated structure

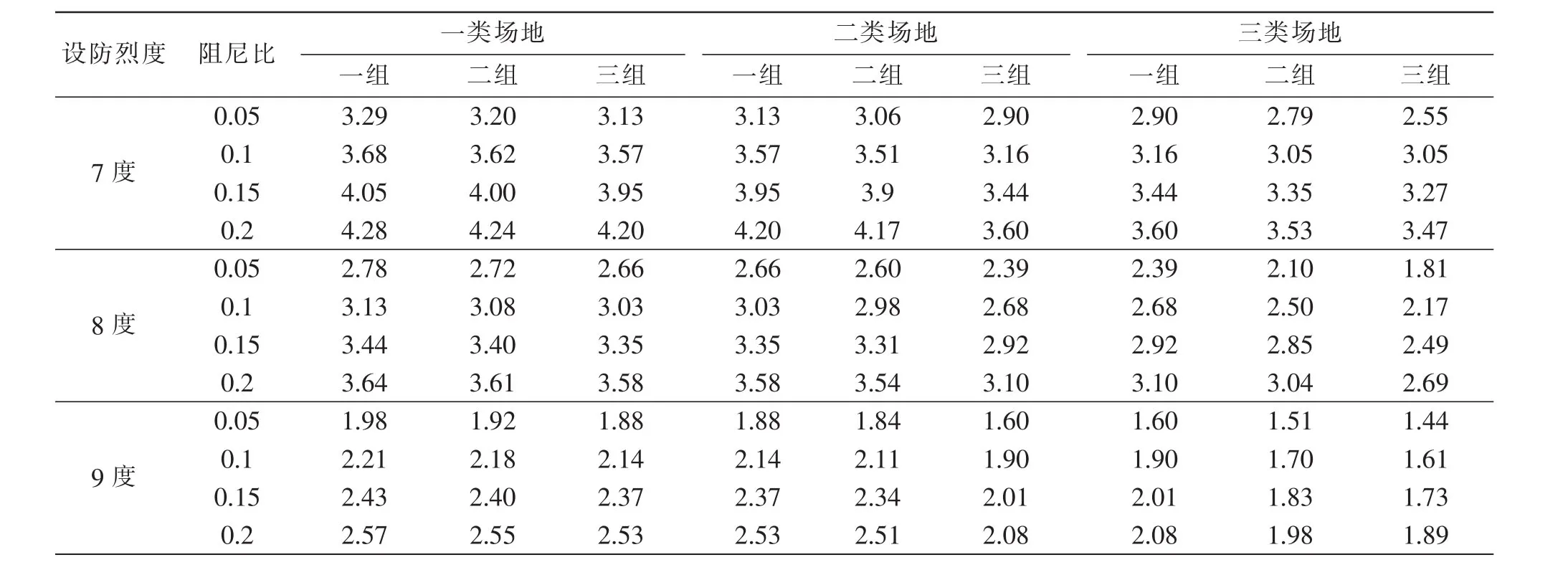
表6 [Δ]为300mm高层隔震结构高宽比限值h/BTable 6 The limit of high-width ratio of high-rise base-isolated structure

表7 [Δ]为400mm时高层隔震结构高宽比限值h/BTable 7 The limit of high-width ratio of high-rise base-isolated structure

5 结语

本文利用高层隔震结构简化模型进行计算，以第一振型对结构产生的影响为主，并按《建筑抗震设计规范》（GB50011-2010）规定，橡胶隔震支座拉应力不超过1 Mpa，压应力不超过30 Mpa，以结构不出现倾覆破坏为前提条件，分析了高层隔震结构在不同的设防烈度、阻尼比、场地类别和地震分组下的高宽比限值。

通过对高宽比限值与结构基本周期的分析得到：对于高层隔震结构，边缘隔震支座上的拉应力不超过1 Mpa时，当Tg＜T11＜5Tg时，高宽比随着结构周期的增大而增大，T11＞5Tg时，高宽比随着结构周期的增大先减小后增大。结构边缘支座压应力不超过30 Mpa时，高宽比限值随结构周期增大而减小。

对于三跨高层隔震结构，计算出了当隔震支座最大容许位移为300 mm和400 mm下的高宽比限值。分析结果为设计高层隔震结构时对高宽比的取值提供参考。

参考文献：

[1]李宏男.采用基础摩擦隔震房屋高宽比限制的研究[J].地震工程与工程震动，1997，17（3）：73-76.

[2]吴香香，孙丽，李宏男.竖向地震动对隔震结构高宽比限值的影响分析 [J].沈阳建筑工程学院学报，2002，18（2）：81-84.

[3]祁皑，范宏伟.基于结构设计的基础隔震结构高宽比限值的研究[J].土木工程学报，2007，40（4）：13-20.

[4]祁皑，商昊江.高层基础隔震结构高宽比限值分析[J].振动与冲击，2011，30（11）：272-280.

[5]祁皑，徐翔，范宏伟.高层隔震结构高宽比限值研究[J].建筑结构，2013，43（6）：50-54.

[6]王栋，吕西林.不同高宽比基础隔震高层结构振动台试验研究及对比分析[J].振动与冲击，2015，17 （3）：109-118.

[7]Anil K.Chopra结构动力学[M].谢礼立，吕大刚，译.北京：高等教育出版社，2007.

[8]祁皑，林于东.改进的基础隔震结构地震作用简化计算方法[J].地震工程与工程振动，2006，26（1）：152-157

[9]杨鹏程.高层框架-剪力墙隔震结构高宽比限值研究及应用[D].广州：广州大学，2016

[10]中华人民共和国住房和城乡建设部.建筑抗震设计规范GB50011-2010[S].北京：中国建筑工业出版社，2010.