《分数四则混合运算》教学设计

程 香

【教学内容】

苏教版六年级上册第五单元例1、练一练。

【教学目标】

1.能结合具体的实例，主动把整数、小数四则混合运算的运算顺序推广到分数四则混合运算中来，并能正确地进行计算。

2.知道整数的运算律对分数运算也同样适用，能应用运算律进行有关分数运算的简便计算。

3.在运用已有知识和经验进行分数四则混合运算和解决实际问题的过程中，进一步丰富对四则混合运算的认识，提高运算能力；积累解决问题的经验，增强应用意识。

【教学过程】

一、四则运算意义回顾

课件逐题出示问题：

1.小明养了20条金鱼，小红养了12条金鱼，两人一共养了多少条金鱼？

2.东东家买来一袋10千克的面粉，吃了4.5千克，还剩多少千克？

学生自由读题后在随堂本上列式。

指名说算式，教师板书，学生说明列式理由。

师：“+-×÷”这四种运算可是咱们的老朋友了，你能谈谈对它们的认识吗？（什么情况下用加法？什么情况下用减法？什么情况下用乘法？什么情况下用除法？）

学生计算，指名说得数。

小结：因为解决问题的需要，就产生了加减乘除这四种运算，这四种运算就统称为“四则运算”。板书：加减乘除 四则运算

【设计意图：借助一步计算实际问题，分别复习“加减乘除”这四种运算的含义与计算方法，让学生认识到虽然参与运算的数是在不断发展的，但是算理并没有改变。】

二、分数四则混合运算顺序沟通

师：整数、小数、分数，参与运算的数在不断发展，问题也会逐渐复杂起来，仅凭一步计算不能解决了。

课件出示：

指名列式，并说明列式理由，教师板书算式及计算过程。

师：有时候两步计算也不能解决了。

课件出示：

指名列式，并说明列式理由，教师板书算式及计算过程。

师：在一道算式中，含有两种或两种以上的运算，就称为四则混合运算。今天我们就来研究分数参与的四则混合运算。

师：你觉得分数四则混合运算的顺序是怎样的呢？

【设计意图：由一步计算到两步计算再到三步计算，帮助学生认识到计算是基于解决实际问题的需要而产生的。因为问题越来越复杂，参与运算的数也越来越多元，分数四则混合运算学习的必要性就得以凸显，运算顺序自然得以沟通。】

三、运算律的推广

1.出示例题：

学生独立列综合算式解决，指名上黑板完成。

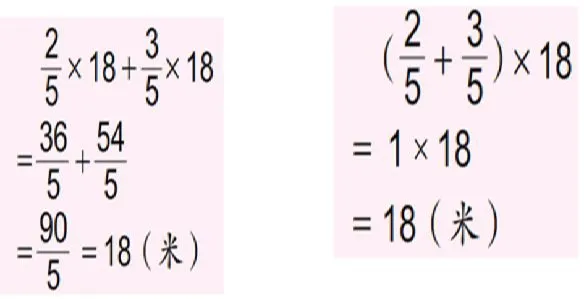
全班交流：学生说说每一步求的是什么？算式之间有什么联系？

教师小结：整数的运算律对于分数同样适用。

2.我们曾经研究过哪些运算定律或者运算性质呢？课件出示

3.学生完成“练一练”第2题:计算下面各题，注意使计算简便。

指名上黑板完成后集体交流。

【设计意图：通过例题两种方法的对比，学生感知曾经学习的运算律也可以使分数四则混合运算变得简便，进而复习曾经学习的运算律，为分数四则混合运算的简便计算做好准备。】

四、巩固提升

1.课件出示“练一练”第1题。

学生独立完成，指名上黑板完成。

2.完成“思考题”。

【设计意图：及时的巩固练习，并且在集体交流中纠错，提高学生灵活运用运算律计算的能力。】

五、全课总结

师：通过这一节课的学习，你有哪些收获？在计算分数四则混合运算时，你想给你的小伙伴一些提醒吗？

【教后反思】

计算课很重要，“+-×÷”贯穿了整个小学阶段的数学教学，譬如本课，就是学生在小学阶段分数运算学习的最后任务，是学生计算技能和能力的重要组成部分，也是进一步学习有理数、分式等运算的重要基础。而在本课之前，学生已经掌握了整数、小数四则运算及四则混合运算的运算顺序及运算律，并能运用运算律进行有关的简便计算。

计算课的内容编排很简单，每册教材中的计算教学基本都会通过问题情境引出计算的需要，在算法的探究中理解计算的道理,在练习中巩固计算方法，提升计算技能。本课也不例外，教材先通过解决生活中常见的实际问题，引入分数四则混合运算，然后学生尝试计算，在尝试中旧知主动迁移。

六年的时间，学生已经有了充分的计算学习的经验，也正因为如此，常规的计算教学很难激发出学生的学习热情，碎片化的计算经验即使迁移过来也不能完整建构。基于这些考虑，本课教学基于教材编排而又突破教材局限，以学生的认知结构发展与计算知识的发展变化为教学的两条主线展开。

从知识的发展变化来看，本课由四道一步计算问题引入，分别复习加、减、乘、除四种运算的含义与计算方法，让学生认识到虽然参与运算的数是在不断发展的，但是算理并没有改变，自然把学生的认知重点引到四则运算的含义上。

问题逐渐复杂，两步计算再到三步计算，帮助学生认识到计算是基于解决实际问题的需要而产生的。“把1升果汁倒满3小瓶，每小瓶升，剩下的平均倒在2个杯子里，每个杯子里倒进果汁多少升？”在解决这个问题时，出现了不同的声音：由1-，到，再到，交流的过程也就是在不断完善建构的过程。就是在这样的交流中，教师及时指出这就是“四则混合运算”，今天学习分数四则混合运算。学生自然而然地经历由四则运算→四则混合运算→分数四则混合运算的知识发展过程中，感受知识的内在联系和结构。

从学生认知结构发展来说，随着知识的复杂，所需要的认知操作也会变得复杂，在由一步到两步运算的时候，显然一步运算的认知结构解决不了当前的两步运算问题。学生通过顺应，认知结构由原先一步扩充到两步，当遇到三步运算时，再由两步扩充到三步，认知结构也不断地扩充。我们的学生，就是在不断面对复杂的知识任务过程中，不断地扩充自己的认知结构，使得学生的认知不断上升发展。当然学生的学习并不只是通过顺应的方式，同化的方式也时常发生，如果学生整数四则混合运算学得很好，就会自然地将过去所学的整数四则混合运算迁移到分数四则混合运算，将分数四则混合运算同化到学生四则混合运算的认知结构下。

无论是从知识还是学生认知角度出发，我们都看到了生长的力量，只有平时培育宽松的课堂土壤，这种自然的生长才会不自觉地迸发。