《平行与垂直》教学设计
2017-04-02陈依琴
陈依琴
【教学内容】
人教版四年级上册第56~57页。
【教学过程】
一、教学平行
1.动手操作:感悟平行间的距离处处相等。
师:昨天我们预习了《平行与垂直》,对《平行与垂直》我们已经有了初步的了解,现在请你拿出两支笔,摆出平行的关系。(全班同学操作后,请一个学生投影展示,同时教师参与)
【设计意图:《平行与垂直》的课例一般都是从分类开始的,那么究竟分类的价值在哪里呢?相对于空间观念的建立哪个更重要呢?我们一般都是呈现一些现象,让学生根据想象去判断是否相交,目的就是要让学生突破直线是可以无限延长的。这样的分类不必要花大力气去做。本课例是在学生预习的基础上直接“摆笔”感悟平行开始的,不但让简单的教学素材真正发挥素材的有效作用,而且使学生充分借助生活经验来感知“平行线之间的距离处处相等”。】
2.视觉观察:借助方格清晰平行特征。
(1)判断:现在这两支笔变成了两条直线,用眼睛来观察,你觉得这两条直线平行吗?
(2)说理:你为什么认为不平行?
预设1:前面的口子大,后面的口子小。
预设2:这两条直线延长以后会相交。追问:你的意思是把直线延长?
(演示延长并看到相交)
师:为什么会相交呢?
(学生表述)
预设1:宽度越来越窄。
提供方格图:

师:发现了什么?
预设2:左边相差2格,右边相差2格不到。
(3)想象平行。
师:假如这两条直线是平行的,想象一下放在方格图上会是什么样的?
生:两边都相差2格。
师:如果都相差3格可以吗?4格呢?
出示:

观察:左边的宽度是2格,右边的宽度是2格,中间的宽度也是2格。
小结:两条直线之间只要距离一样,延长以后都不会相交。

(演示延长)
【设计意图:利用不平行的两条直线去比较,让学生努力去解释为什么不平行,接着引入格子图,让学生直观地观察,发现两条直线的间距从2格,1.5格,半格……,慢慢地、慢慢地靠近直到相交。如果两条直线间一直保持2格会怎样?3格呢?4格呢?应该说学生对于平行线的特征已经很清楚了,理解概念中的“不相交”就显得较为容易了,只要是两条平行线之间的距离永远不变,它们就不会相交。这里利用方格图,形象直观地培养了思维的严谨性,把平行线的特征非常直观地显现出来,让学生感受现有的平行线之间格子数一样,就是距离相等,同时非常有效地帮助学生建立了表象。】
3.阅读:初步建构概念。
师:那你能不能说说看,什么样的两条直线叫平行线?
预测:不相交的两条直线叫做平行线。
师:刚刚同学讲的有一定的道理,我们来看看书上是怎么表述的。
(课件出示书上概念:在同一个平面内不相交的两条直线叫做平行线,也可以说这两条直线互相平行)
说明:直线a和直线b互相平行,直线a是直线b的平行线,直线b是直线a的平行线。
师:比较一下,书上的表述和同学说的有什么不一样?(同一平面)
4.质疑“同一平面”,进一步完善概念。
师:为什么要加“同一平面呢”?这里肯定有一定的道理,现在老师有两把米尺,请1个同学来协助一下,这个同学把米尺放在黑板上,我把米尺放在桌面上,想象一下,一条直线向上下两端无限延长,另一条直线向左右两端无限延长,这两条直线会相交吗?(不相交)是互相平行吗?
师:为了看得更加清楚,我们来看这个长方体:
用实物操作演示:它的正面有一条线,它的上面也有一条线,当这两条直线无限延长,想象会相交吗?(不会相交)
小结:所以刚才的说法都缺了一个重要的条件:“同一平面”。
【设计意图:帮助学生理解“在同一平面内”这一抽象的说法是本节课的教学难点,教学中试图通过两个层次让学生感悟:演示一把米尺竖直放在黑板上,另一把米尺放于一张课桌上,然后让学生将两把米尺想象成两条直线,思考如果无限延长是否会相交,这是第一层次,让学生想象建立初步的感知印象;在此基础上再拿出一个长方体模型(在其正面和上面分别粘有一根可以伸缩的天线,以代表直线的可延长性),进一步演示,从而为学生构建一个良好的空间表象,让学生深刻理解什么是“在同一平面内”。】
5.辨认平行,有效巩固新知。
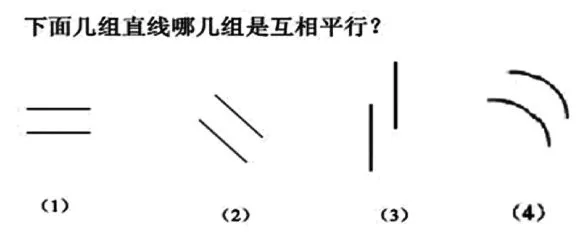
师:第(4)组为什么不是互相平行呢?
师:为什么你认为前3组是互相平行的?
预设:延长以后不会相交。(演示延长)追问:是不是一定要延长以后才能判断?(抓住本质特征就是两条直线的距离相等)
师:这3组平行线有什么不同的地方吗?
小结:看来,互相平行的两条直线不一定是要水平的,可以是各个方向的。
二、教学垂直
1.动手操作,体会相交的多样性及共同点。
师:刚刚我们研究了不相交的情况,现在请你再拿出两支笔,摆一摆相交的情况。
(学生操作)
全班同学操作后,请几个学生上台展示。
预测:如果摆出两支笔不相交的情况,说明把这两支笔想象成了两条直线。
师:你发现他们的摆法都有一个什么共同点?(有交点)这些摆法里面哪一种最特殊?(垂直)
师:你怎么来判定是垂直的?(用三角板或者量角器量一量)
2.表象支撑,聚焦垂直。
感悟相交的多样性及共同特点。
课件呈现一组相交直线:
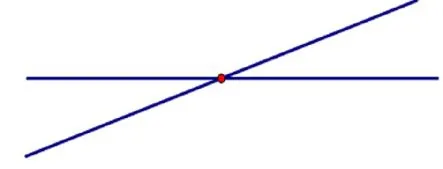
师:现在把两支笔变成了两条直线,两条直线相交一定会形成角。(直接指一指这是什么角)
师:想一想,形成的四个角一定是两个锐角和两个钝角吗?
(学生想象)
课件演示旋转:两条直线绕着交点旋转。
师:仔细观察,你觉得在什么位置上会比较特殊?(垂直,重合)
师:重合,我们一般不研究,我们主要讨论垂直,怎么来判断垂直呢?(用三角板或者量角器量一量)
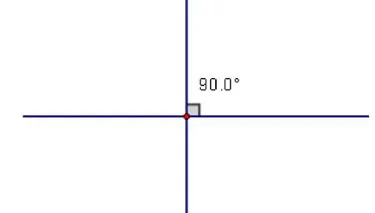
师:这是一个直角,那么其他的三个角是什么角?(学生阐述)
【设计意图:从静态的摆出相交的关系,到动态的展示两条直线相交引起的角度变化,这里充分利用几何画板的动态演示功能和度量功能,很好地让学生感受了两条直线的相交关系,让多媒体资源更好地为教育教学服务。】
3.建构概念。
课件出示垂直的概念:两条直线相交成直角,就说这两条直线互相垂直,这两条直线的交点叫做垂足,其中一条直线叫另一条直线的垂线。
提示:两条直线互相垂直,我们一般用直角符号作标记。

说明:如果把一条直线称作直线a,另一条直线称作直线b,我们说“直线a和直线b互相垂直,直线a是直线b的垂线,直线b是直线a的垂线”。
4.辨认垂直。(既是辨认又是变式,进一步完善垂直概念的练习)
师:现在请你看看这两条直线是互相垂直吗?为什么?

预测:出现两种意见,分别讲解理由。
师:看来我们不能光凭眼睛来判断是否互相垂直,必须利用工具量一量。

(课件制作成一幅一幅的完整图,再缩成不完整的图定格在屏幕上)

师:这两条直线互相垂直,现在其中一条缩到这儿,或者缩到这儿……现在你觉得它们还互相垂直吗?(两种观点说理由)
演示直线延长图:
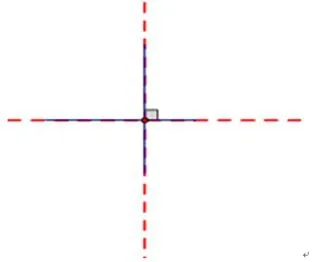
师:不延长可以判断吗?脑子里想象一下延长后的两条直线的关系。
小结:要判断两条直线是不是互相垂直,我们只要看两条直线相交是不是成直角。
【设计意图:在“垂直”的本质上,学生对于“”这种基本形式没有问题,但是对于“、、、”等形式的判断,问题还是相当大的。究其原因主要还是对“垂直”的认识不够深刻,只停留在表面。因此本环节通过几何画板的旋转、拖拉、缩放等功能,让学生感知在同一平面内两条直线的垂直关系是有不同形式的摆法的,进一步使学生感悟“垂直”的本质特点。小练习既发展了学生的空间观念,增强了学生的判断能力,又有效巩固了新知,进一步让学生抓住了判断的本质。】
三、综合应用拓展
找一找:同时出示长方体图和长方体框架
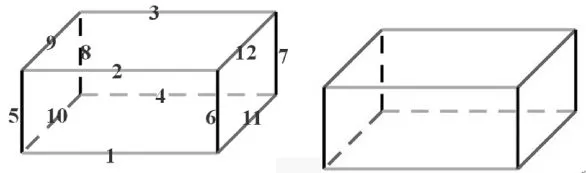
师:你能找到互相平行和互相垂直的线段吗?你能找到几组?
静思默想后,请一个学生说(图),一个学生比划(框架)。
预设:1号线和2号线平行,2号线和3号线平行,1号线和3号线平行……
师:1号线和2号线在哪个平面——正面,2号线和3号线在哪个平面——上面,1号线和3号线在哪个平面——斜面(借助硬板纸演示“同一平面”)。
【设计意图:“在长方体图和长方体框架中,找互相平行和互相垂直的两条线”,引导学生观察、思考、比较,进一步体会线段与线段之间的平行或垂直的关系。这个环节可以一下子拓开学生的思维,让学生更深入地理解垂直与平行及同一平面和不同平面的概念,也为今后学习长方体的概念打下扎实的基础。】
四、课堂总结
师:回忆一下今天这节课,我们研究了同一平面内两条直线的位置关系有哪几种?(板书)
五、回归生活
其实生活中到处都有互相平行和互相垂直的现象,老师收集了几张图,我们一起来欣赏一下。
图片欣赏:

师:你还能举几个这样的例子吗?(学生举例)
【设计意图:让学生找一找、说一说生活中的互相平行与互相垂直的现象,让学生从自己的身边发现数学知识,在培养学生观察能力的同时进一步加深对平行和垂直概念的理解,进一步拓展知识面,也感受了学习数学的意义。】
