知其然并“探”其所以然——《四边形内角和》教学与评析

执教/付 密 评析/刘 莉（特级教师）

【课堂写真】

一、故事导入——激发探究兴趣

师：三角形的内角和是多少度？上节课，我们用了什么方法研究？

视频展示：四边形兄弟今天有场擂台赛：

师：它们在争论什么？（内角和）

板书课题：四边形的内角和。

二、体验过程——探其所以然

1.猜想四边形的内角和。

师：你猜四边形的内角和是多少度？

师：为什么是360°？

生：长方形、正方形比较特殊，它们的4个内角都是直角，内角和是360°（学生边说，课件边展示）。

师：其他四边形的内角和也会是360°吗？你准备用什么方法验证？

2.验证或研究任意四边形的内角和。

（1）验证方法。

（同桌商量验证方法，学生汇报）

生：量一量、拼一拼、分一分。

（2）验证过程。

师：手指尖上出智慧，打开学具袋，小组合作，动手研究吧！

（教师巡视，发现问题，针对性地进行指导研究有困难的学生）

（3）汇报交流。

①量角求和。

学生汇报四边形内角和度数 361°、360°、358°……

师：你发现了什么？

生：这些数据要么等于360°，要么接近360°。

师：为什么量没能得到统一的答案？还有什么方法验证？

②拼角求和。

学生边演示边说明。把4个内角剪下来，拼成一个周角，周角是360°，四边形的内角和是360°。

③分角求和。

师：“四边形”菜地能随便撕吗?还有什么方法验证?

生1：分一分。连接一条对角线，把四边形分成两个三角形。

生2：一个三角形的内角和是180°，两个三角形的内角和是360°，四边形内角和是360°。

师：四边形有4个内角，两个三角形有6个内角，它们的内角和相等吗？为什么?

生：四边形的1个内角分成了三角形的2个内角，四边形的2个内角分成了两个三角形的4个内角，内角和都是360°。

（课件演示）

师：所有四边形内角和都是360°吗?

生：是的，它们都能分成两个三角形。

师：将四边形分成两个三角形，四边形内角和转化成三角形内角和的问题。转化是数学中常用的方法。

3.得出结论：四边形内角和是360°。

师：我们通过3种不同的验证方法，得到同一个结论：四边形内角和是360°。哪种方法最简便、最直接？

生：分一分。“量”容易产生误差；“拼”的应用有限制，考试卷、菜地就不能撕；只有“分”最简便。

三、课堂延伸——推广探究结论的应用

1.基本练习。

出示自制教具四边形。

师：无论怎么拉，虽然形状变了，但内角和都是360°。拉到极限时，两个内角拉成180°，另外两个角拉成0°，内角和是180°+180°+0°+0°=360°。

【设计意图：用推理验证了四边形内角和是360°，同时潜移默化地渗透了极限思想。】

2.升华练习。

将一个四边形分成两个四边形，每个四边形的内角和是多少度？两个四边形合成一个四边形，它的内角和是多少度？

3.类推练习。

学生独立完成计算五边形内角和。

4.举一反三。

师：你准备怎样研究六边形、七边形、八边形……的内角和呢？

生：把多边形分成三角形，看分成三角形的个数就能求出多边形的内角和。

师：千金难买回头看，回到起点看三角形！

三角形个数=边数-2；多边形内角和 =360°×三角形个数；多边形内角和=360°×(边数 -2)。

推导出多边形的内角和后，练习计算十边形、十二边形、一百边形的内角和。

5.拓展练习。

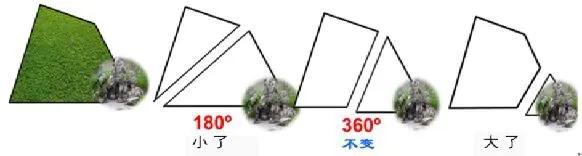
园林工人要重新规划草坪，如果将假山处的内角去掉，剩下多边形的内角和是大了？还是小了？

【课后评析】

《四边形内角和》是2011版教材新增的内容，是基于学生已经知道三角形内角和及四边形基本特征基础上的一次探索规律活动。让学生了解四边形的内角和是360°是《数学课程标准》规定的教学内容和教学要求，这里讲的“了解”不是接受和知道，而是发现并简单应用。学生根据已有经验猜想四边形内角和是360°。为什么是 360°？学生只知其然但不知其所以然，所以，本节课的重点就是要让他们主动地去“探其所以然”——引导学生通过观察、操作、类比、归纳等一系列活动，经历从特殊到一般的探究学习过程，进而研究得出四边形的内角和，尝试解决有关多边形内角和的问题。

著名数学家陈省身先生指出：“数学是自己思考的产物，用自己思考的见解和别人的见解交换，会有很好的效果。”本节课，教师提供给学生一种自我探索、自我思考、自我创造、自我表现和自我实现的机会，使学生最大限度地投入到观察、思考、操作、探究的活动中。在探究是不是所有的四边形的内角和都是360°时，给学生提供一些材料，为学生留有足够的时间和空间，让学生通过小组合作交流，主动探索验证四边形内角和的“猜想”。同学之间通过合作交流、智慧碰撞、思维火花闪现，出现了量一量、拼一拼、分一分推理等多种验证方法，从而得出四边形内角和是360°的重要性质。“是否任何四边形的内角和都是360°呢？”教师趁势再次引导学生同桌合作，动手验证。这样教学，学生不仅经历并感悟了猜想——验证——得出结论——应用的科学研究的过程，而且积累了数学活动经验。更为重要的是，通过这些过程使学生明白：探究问题有不同的方法、途径，并且方法之间可以互为验证，达到结论的统一，从而使学生明白获得探究问题的方法比获得结论更为重要。

我们可以利用方法的“惯性”思考，实现课堂上以尽量小的教学成本取得最大教学效益的目标。当学生已经用量、拼、分三种方法求得四边形内角和，并发现“分”这种方法更科学、方便，也初步体会了四边形内角和与三角形个数之间的关系时，教师提出问题：要求六边形、七边形、八边形……的内角和其实就是要看什么呢？引导学生在探索四边形内角和的基础上利用合情推理和转化的数学思想推导出多边形内角和公式。这样教学，直接将探究四边形内角和的方法类比迁移到其他多边形内角和的研究中，求多边形内角和的问题直接转化为求若干个三角形内角和的问题，学生不用再另起炉灶花费时间思考。

在探究多边形内角和时，表格更容易帮助学生理清题目数量关系，探索规律，总结方法。本节课中，教师通过强化表格的作用，让学生体会到用表格解决问题的奇妙。