抑制性突触输入对神经元发放率响应的影响

李 生, 焦贤发

(合肥工业大学 数学学院,安徽 合肥 230009)

抑制性突触输入对神经元发放率响应的影响

李 生, 焦贤发

(合肥工业大学 数学学院,安徽 合肥 230009)

文章基于整合发放神经元模型,研究抑制性突触输入和外部周期刺激对神经元发放率的影响。数值结果表明:在突出输入等于阈值时,适当频率的抑制性突触输入对神经元发放率具有易化作用,对神经元发放率峰值具有延迟作用;在突出输入小于阈值时,抑制性突出输入抑制神经元膜电位发放;在外部刺激作用下,神经元发放率幅值与外部刺激有关,刺激频率越高,发放率幅值越小,刺激强度越大,发放率幅值越大。

突触输入;外部刺激;瞬时发放率;泊松过程;概率流

在神经网络中,神经细胞之间通过“突触”连结,实现神经兴奋信号的传递。对于大多数神经元来说,突触又是其神经信号的输入重要渠道,神经元都通过突触部位接受所有前级细胞传递关于自身兴奋性和抑制性状态的有关信息。关于突触部位的研究,突触输入如何影响神经元膜电位和发放率一直是研究的热点课题。神经元一般接受兴奋性和抑制性突触输入,当膜电位达到阈值时,发放动作电位。通过分析神经元发放率响应研究突触输入作用[1]。在兴奋性突触输入弱或强2种状态下,研究发现神经元发放率和膜电位对突触输入电流都比较敏感[2]。为了研究突触输入对发放率的影响,很多学者提出了相关计算方法和理论。在整合发放模型中,对于高频低振幅突触输入,经常描述成泊松过程,并运用扩散近似法简化神经元模型[3-6]。文献[7]运用的首达时间和膜电位概率密度函数的Fokker-Planck方程研究分析了发放率分布；当突触时间常数较大,突触时间很长的情况下,文献[6]提出研究有突触过滤作用的整合发放神经元响应性反应的方法,并且估计不同突触时间常数的神经元发放率；文献[8]数值模拟得到了所有兴奋性突触输入与抑制性突触输入相关时间常数对应的神经元发放率,分析了相关时间常数对发放率的影响。

在神经系统中兴奋性神经元和抑制性神经元相互作用,抑制性神经元通过释放抑制性化学递质,影响突触后神经元膜电位的发放,虽然抑制性神经元数目相比兴奋性神经元只是少数,但它们对神经元发放率动态演化是极其重要的。突触抑制性可以影响大脑皮层神经元认知功能, 文献[9]研究了大脑皮层抑制性神经元的特殊作用，有助于理解抑制性神经元对精神病或者认知混乱的作用。整合发放神经元模型(IF模型)是H-H模型简化形式,该类模型能够比较精确地反映单个神经元电学特征和外部输入的响应[10];文献[11]基于该模型研究发现抑制性突触输入影响神经元发放的阈值,从而影响输入输出曲线,抑制性突触输入通过减少突触输入均值及增加突触输入标准方差,增加峰峰间距的可变性。学者们仅研究了突触抑制性对神经元发放峰峰间距可变性影响,没有具体研究突触抑制性对神经元发放率动态演化的影响。然而,在现实世界中,外部干扰是普遍存在的,许多学者在研究突触输入对神经元响应性反应影响时,考虑外部周期刺激作用, 文献[12]运用首达时过程统计和发放率功率谱密度2种统计方法,分析了突触噪声和外部周期刺激之间的相互作用对随机振荡现象的影响。本文在IF模型的基础上,进一步研究外部周期刺激和抑制性突触输入作用下,整合发放神经元发放率的动态演化。

1 数学模型

在神经系统里,神经元接受突触输入既有兴奋性也有抑制性,同时会受到外部刺激作用,本文考虑神经元集群中某个神经元膜电位V(t)动态演化方程,即

(1)

其中,V(t)为神经元的膜电位;τ为膜时间常数;Je、Ji分别为兴奋性和抑制性突触后膜电位的振幅;A为外部周期刺激强度;w为外部周期刺激频率;tk(k=1,2,…)、tj(j=1,2,…)分别为第k个兴奋性突触脉冲输入时间和第j个抑制性突触脉冲输入时间;δ(t-tk)、δ(t-tj)分别为2个相互独立的脉冲序列。设ve、vi分别表示兴奋性突触输入频率和抑制性突触输入频率。

在单个神经元突触部位接受高频的突触输入情况下,(1)式中脉冲时间序列扩散近似表示为:

(2)

(3)

把(2)式代入(1)式中,得到神经元膜电位的简化方程为:

(4)

其中,η(t)为高斯白噪声随机过程,〈η(t)η(t′)〉=δ(t-t′);μ为突触输入之和;σ为噪声强度;τ为膜时间常数。

相应于方程(4)的Fokker-Planck方程为:

(5)

方程(5)也可以写成：

(6)

其中,J(V,t)为概率流,概率流J(V,t)的本构方程为:

(7)

当膜电位达到阈值时,对应的概率流量是神经元瞬时发放率,即

(8)

为了得到方程(8)的数值解,考虑吸收边界条件:

(9)

由(7)～(9)式得出神经元瞬时发放率为:

(10)

由(10)式得到神经元瞬时发放率为:

(11)

2 数值模拟

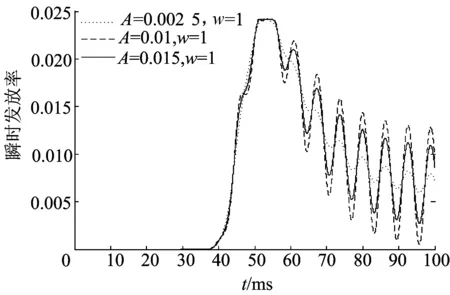
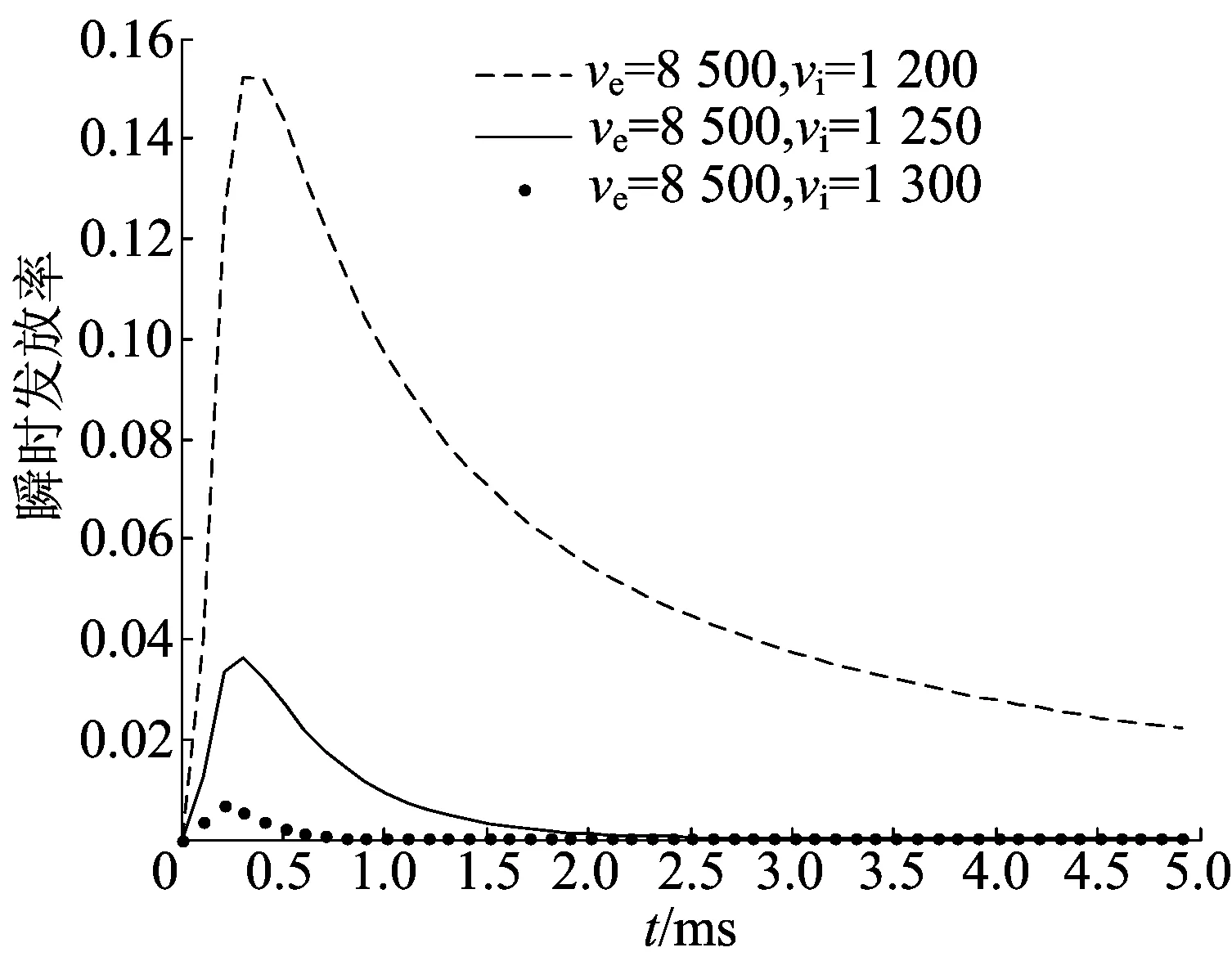
由于当μτ>Vth时,在没有噪声项ση(t)和外部周期刺激Acos(wt)的影响下,突触输入足以使神经元膜电位到达阈值,发放动作电位[11,13]。本文主要研究在μτ≈Vth和μτ

2.1μτ≈Vth情况下的数值模拟分析

(1) 当参数τ=10,V0=3,Vth=18,Je=0.000 9,Ji=0.000 015时,突触抑制性输入对神经元发放率的影响如图1所示。

图1 突触抑制性输入对神经元发放率的影响

从图1可以看出,当无抑制性突触输入情况下(Ji=0),神经元发放率迅速增大到峰值后再逐渐衰减。当接受抑制性突触输入时,神经元发放率峰值有明显延迟。这表明突触抑制性对神经元发放率峰值具有延迟作用。

其他参数不变,当无外部刺激作用时,在不同抑制性突触输入频率下,神经元发放率随时间演化过程如图2所示。

图2 不同抑制性突触输入频率 对神经元发放率的影响(μτ≈Vth)

从图2可以看出,当抑制性突触输入频率越大,神经发放率峰值延迟时间就越长。当抑制性突触输入频率增大,达到稳定状态的神经元发放率增大。这说明在突出输入近似等于阈值情况下,适当的抑制性突触输入频率对神经元发放率具有易化作用。

(2) 当参数τ=10,Je=0.000 9,V0=3,Vth=18，Ji=0.000 015,ve=2 000,vi=100时,对应于不同外部刺激强度的神经元发放率随时间的变化如图3所示。

图3 不同强度刺激对神经元发放率的影响(μτ≈Vth)

从图3可以看出,外部刺激改变了神经元发放幅值,随着外部刺激强度增大,神经元发放率幅值增大。这表明外部刺激加强了神经元发放活动。神经元发放率迅速达到峰值,随着时间增加,神经元发放率出现振荡衰减模式,神经元发放率逐渐达到平稳振荡。表明随着时间增加,外部刺激作用明显增强。

其他参数不变,在不同外部刺激频率下,神经元发放率随时间演化的过程如图4所示。

图4 不同频率刺激对神经元发放率的影响(μτ≈Vth)

从图4可以看出,刺激频率改变了神经元发放率幅值,增大外部刺激频率,神经元发放率幅值会变小。然而,在高频外部刺激下,神经元发放率幅值极小,这表明外部刺激频率是影响神经元发放率幅值的重要因素之一。

2.2μτ

(1) 当参数τ=10,Je=0.05,Ji=0.36,V0=7,Vth=20时,无外部刺激作用时,对应于不同抑制性突触输入频率的神经元发放率随时间的演化过程如图5所示。

图5 不同抑制性突触输入频率 对神经元发放率的影响(μτ

从图5可以看出,神经元发放率先迅速达到峰值,然后不断衰减。当抑制性突触输入频率变大,神经元发放率的峰值变小。这表明当突触输入低于阈值时,在抑制性突触输入的作用下,兴奋性神经元膜电位发放受到抑制。

(2) 当参数τ=10,ve=8 500,vi=1 200,Je=0.05,Ji=0.36,V0=7,Vth=20时,在不同的外部刺激强度下神经元发放率随时间的变化如图6所示。

图6 不同强度刺激下对神经元发放率的影响(μτ

从图6可以看出,神经元发放率幅值与外部刺激强度有关,外部刺激强度增大,神经元发放率的幅值随之增大。

其他参数不变，不同频率刺激对神经元发放率的影响如图7所示。

图7 不同频率刺激对神经元发放率的影响(μτ

从图7可以看出，在外部刺激作用下,神经元发放率发生明显的改变,神经元发放率迅速达到峰值,随着时间增加,神经元发放率幅值越来越小。这表明随着时间增加,外部刺激作用不断减弱。神经元发放率幅值与外部刺激频率相关,外部刺激频率越大,神经元发放率幅值越小。

3 结 论

外部刺激对神经元发放率幅值的影响依赖于刺激频率、刺激强度。增大外部刺激频率,会减小神经元发放率振荡幅值,增大外部刺激强度,会增大神经元发放率振荡幅值。抑制性突触输入对神经元发放率有影响,在突触输入等于阈值的情况下,适当频率的抑制性突触输入对神经元发放率有易化作用,对神经元发放率峰值有延迟作用;在突触输入低于阈值情况下,抑制性突触输入抑制神经元膜电位的发放。

[1] RICHARSON M J E,SWARBRICK R.Fring-rate response of a neuron receiving excitatory and inhibitory synatic shot noise[J].Physical Review Letters,2010,105(17):178102-1-178102-4.

[2] ROSENBAUM R,JOSIC K.Menbrane potential and spike train depend distinctly on input statistics[J].Physical Review E:Statistical,Noninear and Soft Matter Physics,2011,84(5):051902-1-051902-10.

[3] HOHN N,BURKITT A N.Shot noise in the leaky integrate-and-fire neuron[J].Physical Review E:Statistical,Noninear and Soft Matter Physics,2001，63(3):031902.

[4] YIM M Y,AERTSEN A,ROTTER R.Impact of intrinsic Biophysical diversity on the activity of spiking neurons[J].Physical Review E:Statistical,Noninear and Soft Matter Physics,2013,87(3):032710-1-032710-5.

[5] RICHARDSON M J E.Effect of synaptic conductance on the voltage distribution and firing of spiking neurons[J].Physical Review E:Statistical,and Soft Matter Physics,Noninear,2014,69(5):051918-1-051918-8.

[6] MORENO-BOTE R,PARGA N.Role of synapic filtering on the firing response of simple model neurons[J].Physical Review Letters,2004,92(2):028102-1-028102-4.

[7] BURKITT A N.A review of the integrate-and-fire neuron model:II.inhomogeneous synaptic input and network properties[J].Biological Cybernetics,2006,95(2):97-112.

[8] MORENO R,DELAROCHA J,RENART A,et al.Response of spiking neurons to correlated input[J].Physical Revie Letters,2002,89(28):288101-1-288101-4.

[9] ISAACSON J S,SCANZIAN M.How inhibition shapes cortical activity [J].Neuron,2011,72(2):231-243.

[10] 王锋,焦贤发.整合发放神经元模型突触输入参数估计[J].合肥工业大学学报(自然科学版),2015,38(3):428-432.

[11] LADENBAUER J,AUGUSTIN M,OBERMAYER K.How adaptation current change threshold,gain and variability of neuronal spiking[J].Journal of Neurobiology,2014,111(5):939-953.

[12] BULSARA A R,LOWEN S B,REES C D.Collective behavior in the perodically modulated wiener process:noise-induced complexity in a model neutron[J].Physical Review E,1994,49(6):4989-5000.

[13] LANSKY P.Sources of periodical force in noisy integrate-and-fire of neuronal dynamics[J].Physical Review E,1997,55(2):2040-2043.

(责任编辑 张 镅)

Impact of synaptic inhibition on firing-rate response of neurons

LI Sheng, JIAO Xianfa

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

In this paper, the integrate-and-fire model is applied to studying the effect of synaptic inhibition and periodic external stimulus on neuron firing-rate. The numerical results show that when synaptic input is equal to the threshold, the appropriate frequency of synaptic inhibition has facilitation effect on neuron firing-rate and causes a delay to the peak of firing-rate. When synaptic input is less than the threshold, synaptic inhibition restrains neuron membrane potential. Under the effect of external stimulus, the amplitude of firing-rate is related to external stimulus. When the stimulus frequency becomes higher, the amplitude of firing-rate will become lower, when the stimulus amplitude becomes higher, the amplitude of firing-rate will become higher.Key words:synaptic input; external stimulus; instantaneous spiking rate; Poisson process; probability flux

2015-10-26；

2016-01-13

国家自然科学基金资助项目(11172086;11232005)

李 生(1989-),男,安徽阜阳人,合肥工业大学硕士生; 焦贤发(1965-),男,安徽安庆人,博士, 合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.02.025

O29

A

1003-5060(2017)02-0272-05