融会贯通提升思维——《平面图形的面积整理与复习》教学设计与评析

鲍赛红　吴恢銮

【教学内容】

浙教版五年级上册第四单元。

【教学过程】

一、回忆梳理，引入新知

师：课前我们进行了平面图形知识的整理。我们学过的平面图形有哪些？怎样计算它们的面积？

（出示平行四边形、三角形、梯形）

（展示这三种图形的面积推导方法，逐一回顾各种平面图形的面积推导过程）

师：平行四边形、三角形、梯形面积公式的推导过程有什么相似之处？

生：都运用了转化的策略。

师：当我们遇到新问题时，可以想办法将它转化成我们已经学过的知识，然后用学过的知识去解决新的问题。

【评析：整理复习课不仅是识记公式并运用公式解决常见的练习题，更重要的是将学过的知识进行系统整理使其形成知识与方法的思维网络，便于提取与应用。在自主整理知识的过程中发现遗漏的知识应及时弥补，如果生长出新的知识则适当拓展。上课伊始，鲍老师即引导学生回忆梳理每个平面图形的面积公式，并让学生表述面积公式的推导过程。从点入手、连点成线，为沟通三个图形面积公式之间的内在联系做好知识与思考方法的铺垫准备。】

二、打通联系，融会贯通

师：三个平面图形的面积公式可以少记几个吗？它们之间有什么关系？有没有可能把三个不同的平面图形转化成同一个面积公式来计算呢？

1.从平行四边形面积公式出发，提炼转化思想。

生：两个相同的梯形或者三角形都能拼成平行四边形。所以我认为可以统一利用平行四边形的面积公式来计算三种图形的面积。

（根据学生的回答，出示三角形和梯形面积公式与平行四边形面积公式之间的关系）

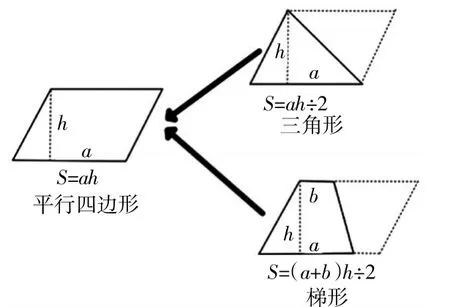
2.从梯形面积公式出发，渗透运动变化思想。

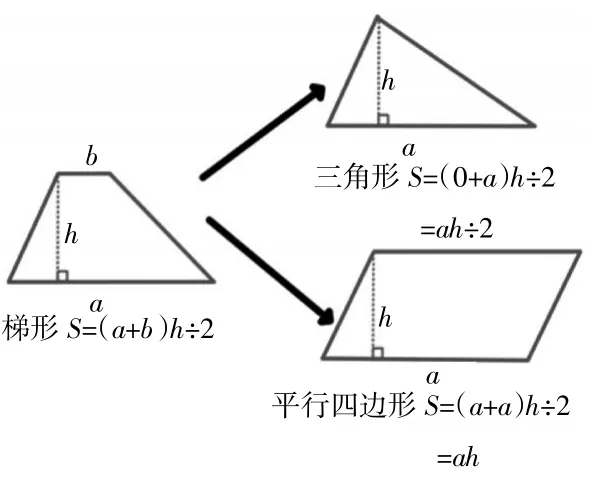
生：我认为可以统一用梯形面积计算公式。“梯形的面积=（上底+下底）×高÷2”，当上底缩短至0时，梯形就变成了三角形，公式就变成了“下底×高÷2”，也就是“三角形的底×高÷2”。而当上底变得和下底一样长时，梯形就变成了平行四边形，公式就变成了“上底（或下底）×2×高÷2=底×高”。

教师根据学生的回答板书，让学生明晰梯形面积公式与平行四边形、三角形面积公式之间的关系。

3.从三角形面积公式出发，提炼等积变形思想。

师：从这两个转化过程中你还想到了什么？挑战一下，能否用三角形的面积计算公式来计算梯形和平行四边形的面积？

出示学习要求：

（1）分一分：把梯形和平行四边形分成几个三角形？

（2）算一算：请用字母表示分成的三角形，并算一算。

（3）想一想：能不能把分成的多个三角形变成一个三角形？

（独立探究后四人小组相互交流，然后全班交流）

组1：先把梯形分成两个三角形，于是这个梯形的面积就变成了两个三角形的面积，一个三角形的面积是ah÷2，另一个三角形是bh÷2，合在一起就是 ah÷2+bh÷2=（a+b）h÷2。

组2：（使用白板软件，边演示边讲解）先把梯形中以b为底的三角形翻转，然后通过等积变形，把以b为底的三角形上面的顶点沿平行线左移，直到和以a为底的三角形的上面这个顶点重合，这样两个三角形就变成了一个三角形（如下图）。三角形的底是梯形的上底加下底的和，三角形的高就是梯形的高。

师：好厉害！像这样，图形形状发生了变化，面积没有发生变化，我们称之为——等积变形。有没有小组想到平行四边形是怎么变的呢？

生：听了组2的介绍，我想到了（使用白板软件，边演示边讲解）先把平行四边形沿对角线分成两个三角形，把其中一个三角形翻转，然后等积变形成这样的三角形（指下图右三角形）。三角形的底就是原平行四边形的底的两倍，三角形的高就是原平行四边形的高。

师：看看变形以后的情况，它们之间到底有怎样的关系呢？

4.小结：三个面积计算公式可以通过扩倍拼补的方法转化成平行四边形面积计算公式，通过运动变化的方法转化成梯形的面积计算公式，还可以通过等积变形转化成三角形的面积计算公式。

【评析：鲍老师引导、鼓励学生借助图形操作，沟通三个图形面积之间的关系，运用现成的公式，从扩倍拼补、运动变化以及等积变形三个维度分析内在联系，使之在知识上求联、在方法上求通，开放中有统一、统一中有开放，极大地激发了学生探究的兴趣、提升了学生探究的水平、发展了学生的思维。小组的讨论、集体的碰撞、白板技术的辅助等，使用得恰到好处，适得其所。】

三、层次练习，应用提升

1.基本练习。

在下图中，当a缩短成一个点，也就是a=0时，这个图形就变成了（）形，公式S=（a+b）h÷2就变成了（）；当a=b时，这个图形就变成了（），公式 S=（a+b）h÷2 就变成了（）。

他父亲有三个要好的朋友，一个是大学教授、物理学家克里斯坦森，一个是哲学家霍夫丁，另一个是语言学家汤姆森。每逢星期五的晚上，他们三人都要到波尔家做客，他们在一起兴致勃勃地谈论物理、哲学、文学，评说科学领域的新成就。

2.变式练习。

已知梯形面积①和三角形面积②相等，求AB的长？（单位：厘米）

3.拓展练习。

求阴影部分的面积。

【评析：三组练习从基本到变式、从变式到拓展，既是巩固新知识、新方法，又是在变中训练不变。第一题从运动变化的角度，沟通梯形与平行四边形、三角形之间面积的关系，属于课堂知识的回顾。第二题，左图：梯形和三角形的高相等，则面积相等就意味着梯形上下底的和=三角形的底，从而AB=12-7=5；右图，基本原理同左图，7+AB=12-AB，AB=2.5。第三题，左图通常的做法是：（4+3）×3÷2-3 ×3 ÷2=6（cm2），也可以通过等积变形，构造三角形ABD的面积=三角形ABC面积，从而阴影部分的面积就是 4×3÷2=6（cm2）。右图AC//GE，从而三角形GAE的面积=三角形GCE的面积=6×6÷2=18（cm2）。

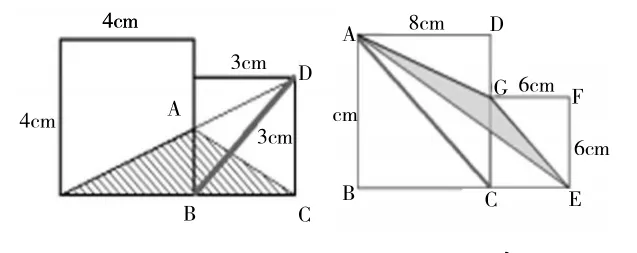
显然，二、三题需要学生对前面公式整理中涉及到的系列推理方法，尤其是等积变形等灵活地进行应用。】

四、课堂总结，畅读收获

师：这节课你有哪些新的收获？